当前位置：首页 > news >正文

互联网公司哪个部门负责网站建设/在线培训系统平台

news 文章来源：https://blog.csdn.net/ComputerInBook/article/details/129424559 2025/3/13 3:34:56

互联网公司哪个部门负责网站建设,在线培训系统平台,侵入别人的网站怎么做,湖北营销型网站建设价格第15章傅里叶定理(Fourier’s Theorem) Fourier, not being noble, could not enter the artillery, although he was a second Newton. (傅立叶出生并不高贵，因此按当时的惯例进不了炮兵部队，虽然他是第二个牛顿。) —Franois Jean Dominique Arag…

第15章傅里叶定理(Fourier’s Theorem)

Fourier, not being noble, could not enter the artillery,

although he was a second Newton.

(傅立叶出生并不高贵，因此按当时的惯例进不了炮兵部队，虽然他是第二个牛顿。)

—François Jean Dominique Arago

自两千多年前三角学问世以来，它已经走过了漫长的道路。但是有三个发展，比其他所有发展都更突出，从根本上改变了这个科目：Ptolemy的弦表，它将三角学转变为一门实用的计算科学；De Moivrep定理以及Euler公式 $e^{ix} = cos(x)+isin(x)$ , Euler公式将三角学、代数学、以及分析学融合在了一起；以及Fourier定理，本书最后一章专门探讨这个定理。

Jean Baptiste Joseph Fourier 于1768年3月21日出生在法国中北部的欧塞尔(Auxerre)。九岁时，他的父母双双去世。受家族中一些朋友的影响，傅里叶考入了本笃会(Benedictine order)开办的军事学校，在那里他表现出早期的数学天赋。法国有着培养伟大科学家的悠久传统，他们也在军队中为国家服务：勒内·笛卡尔(René Descartes，1596-1650 年)，一位从军人转变为哲学家的人，他发明了解析几何(analytic geometry)；加斯帕尔·蒙日(Gaspard Monge,1746-1818 年)，他发展了画法几何(descriptive geometry)，并于1792年成为海军陆战队(marines)部长；简· 维克托· 庞塞莱(Jean Victor Poncelet,1788-1867)，他在1812年拿破仑(Napoleon)从莫斯科撤退后成为战俘时写下了他关于射影几何(projective geometry)的伟大著作；以及两个“Carnots”，一个是几何学家拉扎尔·尼古拉斯·玛格丽特·卡诺(Lazar Nicolas Marguerite Carnot，1753–1823)，他成为法国最伟大的军事领袖之一，另一个是他的儿子物理学家尼古拉斯·莱昂纳德·萨迪·卡诺(Nicolas Léonard Sadi Carnot, 1796–1832)，他作为军事工程师开始了他的军旅生涯，后来奠定了热力学的基础。而年轻的Fourier希望遵循传统成为一名炮兵军官。但由于他的社会阶层不许(他的父亲是一名裁缝)，他只能在军校获得数学讲师职位。然而，这并没有阻止他参与公共生活：他在 1789 年积极支持法国大革命，后来因为恐怖事件的受害者辩护而被捕，勉强逃过断头台。最终，Fourier因其活动而获得奖励，并于1795年在著名的(prestigious)巴黎综合理工学院(École Polytechnique in Paris)获得教授职位，当时，拉格朗日(Lagrange)和蒙格(Monge)也在那里任教。

1798年拿破仑·波拿巴皇帝(Emperor)在埃及发动了伟大的军事行动。作为一个对艺术和科学有着广泛兴趣的人，拿破仑邀请了几位著名的学者加入他的行列，其中包括蒙格和傅立叶。傅里叶被任命为埃及南部总督，并以此身份组织了法国占领军的工作坊(workshops)。1801年法国败给英国人后，他返回家乡并成为格勒诺布尔(Grenoble)地区的行政长官(prefect)。他的行政职责包括监督道路建设和排水工程(drainage projects)，所有这些他都以出色的能力执行。如果这还不够让他忙碌的话，他还被任命为埃及研究所的秘书，并于1809年完成了一部关于古埃及的重要著作<<Préface historique>>(历史序言)。

人们常常惊叹于 18 和 19 世纪许多学者的广泛活动。就在Fourier履行其行政职责的同时，他正深入地从事他的数学研究。他在两个看似无关的领域工作：方程理论(the theory of functions)和数学物理学(mathematical physics)。在年仅16岁时，他就多项式的正根和负根的个数找到了笛卡尔符号规则的新证明。他的证明成为现代代数课本中的标准证明。他开始着手编写一本名为<<Analyze des équations déterminées>>(方程判定分析)的书，其中他预见了线性规划。然而，Fourier在完成这部作品之前就去世了(它由他的朋友路易斯·玛丽·亨利·纳维尔(Louis Marie Henri Navier)编辑出版，于1831年出版)。他还开创了量纲分析(dimensional analysis)——基于它们之间的量纲研究物理量之间的关系。

但正是在数学物理学中，Fourier留下了他最伟大的印记。他对热量从高温区域流向低温区域的方式特别感兴趣。牛顿已经研究过这个问题，并发现物体的冷却速度(温度下降)与其周围环境的温度差成正比。然而，牛顿冷却定律仅适用于温度的时间变化率，而不适用于它的空间变化率或梯度。后一个量取决于许多因素：物体的热导率、几何形状和边界上的初始温度分布。要处理这个问题，必须使用连续统的分析工具，特别是偏微分方程)(partial differential equations)(见第 53 页)。Fourier表明，要求解这样一个方程，必须将初始温度分布表示为无穷多个正弦项和余弦项的总和——三角级数(trigonometric series)或Fourier级数(Fourier series)。Fourier早在1807年就开始研究这个主题，后来在他的主要著作<< Theorié analytique de la chaleur>>(Analytic theory of heat，热分析理论，1822年)中进一步扩展，成为19世纪一些伟大的关于数学物理论文的模型。

Fourier于1830年5月16日在巴黎不幸从楼梯上坠落身亡。他的几幅画像留存了下来。一尊1831年创作的半身像在二战中被摧毁。第二座半身像于1849 年在他的家乡竖立，被德国占领者熔化，他们将这种金属用作武器；但欧塞尔市长得知灾难迫在眉睫的消息，并设法抢救了半身像的两个浅浮雕，幸运的是它们幸免于难。1844年，考古学家 Jacques Joseph Champollion-Figeac(序言中提到的埃及学家(Egyptologist)Champollion的兄弟)撰写了Fourier的传记(biography)，题为<<Fourier, Napoleon et les cent jours>>(傅立叶、拿破仑等人)。[1]

Fourier在他的工作中，不仅受到纯数学考量思想的指引，而且受到他对物理原理的全面透彻(sound)掌握的指引。他的座右铭(motto)是：“对自然的深入研究是数学发现最丰富的源泉(Profound study of nature is the most fertile source of mathematical discoveries)。” 这招致了Lagrange、Poisson和Biot等纯粹主义者的尖锐批评，他们攻击他称其“缺乏严谨性”；然而，有人怀疑政治动机和个人竞争也起了一定作用。具有讽刺意味的是，Fourier在数学物理学方面的工作后来导致了所有数学创作中最纯粹的一个——康托尔(Cantor)的集合论(set theory)。

Fourier定理背后的基本思想非常简单。我们知道，函数cos(x)和sin(x)都具有周期2π，并且在一般情况下，函数cos(nx)和sin(nx)具有周期 $\frac{2\pi}{n}$ 。但是，假如我们组成这些函数的任意线性组合(linear combination)——即，用常量乘以每一项再将其结果相加——这个新构成的函数仍然具有周期2π(图92)。这将我们引向下面的观察现象：

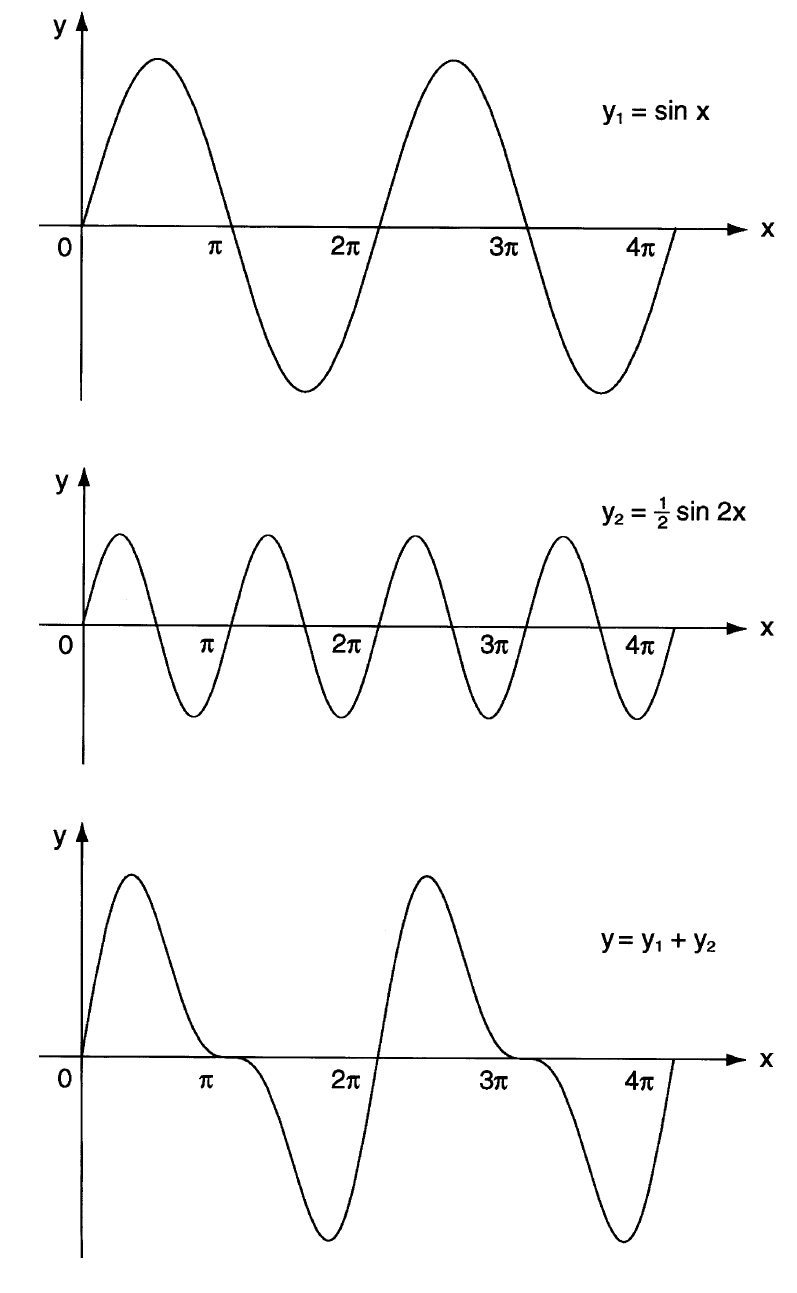
--------------图92 sin(x), sin(2x)/2 以及它们的和的函数图像--------------------

令f(x)为任意具有周期2π的具有“合理行为”的函数；即，满足对于所有在其定义域中的x ，都有f(x + 2π) = f(x)。[2] 我们可以构造“有限(finite)”和的表达式：

$S_n (x) = \frac{a_0}{2} + a_1cos(x) + a_2cos(2x) + a_3cos(3x) + ... + a_ncos(nx) + b_1sin(x) + b_2sin(2x) + b_3sin(3x) + ... + b_nsin(nx) =\frac{a_0}{2}+\sum_{m=1}^{n}[a_{m} cos(mx)+b_{m}sin(mx)]$ ,

-------------------------------------------------------------------------(1)

其中，系数 $a_m$ 和 $b_m$ 是实数( $a_0$ 为什么要除以2在后面读者会明白)；S(x)的下标n表明，这个和取决于正弦项和余弦项出现的数量。既然 $S_n(x)$ 是cos(mx)和sin(mx)(m = 0, 1, 2, 3,......)各项之和，那么它就是具有周期为2π的x的函数。显然，这种函数的特征取决于系数 $a_m$ 和 $b_m$ (以及n)。我们现在问：确定这些系数使其求以下和是否可行：(1) 对大的n,在区间-π < x < π 近似已知函数f(x)是否可行？换句话说，我们是否可以确定 $a_m$ 和 $b_m$ ,使其对于区间-π < x < π上的每一个点，都满足下列近似表达式？

$f(x) \approx \frac{a_0}{2}+\prod_{m=1}^{n}[a_{m}cos(mx)+b_{m}sin(mx)],$

---------------------------------------------------------------------------(2)

显然，我们要求这个近似函数应该随着n的增加而改变，并且随着n->∞它应该变成一个等式；即，

$\lim_{n->\infty}S_{n}(x) = f(x)$ 。假如这确实可行，我们就说级数(2)收敛(converges)于函数f(x)，并且可以写作

$f(x) = \frac{a_0}{2}+\prod_{m=1}^{n}[a_{m}cos(mx)+b_{m}sin(mx)]$ 。

---------------------------------------------------------------------------(3)

在接下来，我们假设级数(2)确实可以在区间-π < x < π上收敛于函数f(x)，[3] 我们将展示如何确定这个系数。[4] 我们以下面三个积分公式为出发点

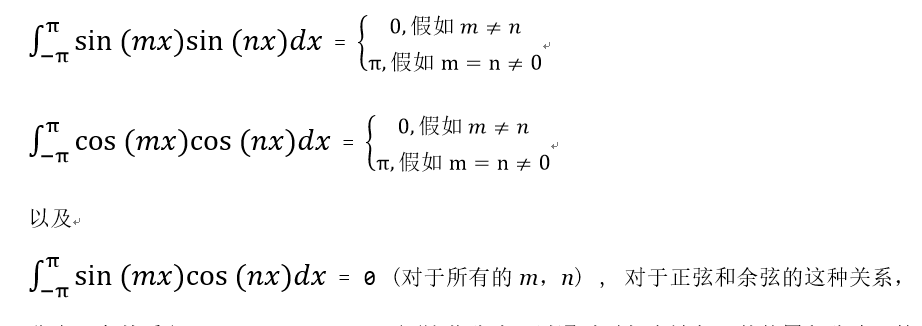
称为正交关系(orthogonality relations)(这些公式可以通过对每个被积函数使用积公式，然后分别对每个项进行积分来证明；注意，当m和n都为零的时候，第二个公式的积分是1,因此我们得到

$\int_{-\pi}^{\pi}dx = 2\pi$ 。

为了求得m = 0,1,2,...时的系数 $a_m$ ，我们用cos(mx)乘以等式(3)并在区间-π < x < π上逐项积分。[5] 鉴于其正交关系，右边的所有项除了项 $(a_{m}cos(mx)).cos(mx) = a_{m} cos^{2} (mx) = a_{m}\frac{1+cos(2m)x}{2}$ 之外,其它项都为0,其从-π 到 π的积分为 $\pi a_{m}$ 。因此，我们得到

$a_{m} = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x)cos(mx)dx,m = 1,2,3, ...$ 。--------------------------------------(4)

为了求得 $a_0$ ，我们重复这个步骤；但是，既然我们现在有m = 0，用cos(0x) = 1乘以等式(3),则等式(3)保持不变，因此，我们只是将它在-π 到 π积分；再次地，右边的所有项除了 $(\frac{a_0}{2})\int_{-\pi}^{\pi}dx = (\frac{a_0}{2})2\pi = \pi a_0$ 。因此，我们得到

$a_{0} = \frac{1}{\pi} \int_{-\pi}^{-\pi}f(x)dx$ 。-------------------------------------------------------------------------(5)

注意，等式(5)是等式(4)在m = 0时的情况；这就是为什么在等式(3)中选择 $\frac{a_0}{2}$ 作为常量项的原因。假如我们选择 $a_{0}$ 作为常量项，等式的右边将必须除以2。

最后，为了求得 $b_m$ ,我们用sin(mx)乘以等式(3)并再次在区间-π < x < π上逐项积分；结果是

$b_m = \frac{1}{\pi}\int_{-\pi}^{\pi}sin(mx)dx$ , m = 1, 2 , 3,..., 。--------------------------------------------------(6)

等式(4)到等式(6)是著名的Euler公式(没错，另外两个以公式也以Euler的名字命名！)，它们允许我们找到傅里叶级数的每个系数。当然，取决于f(x)的性质，实际的积分可以或不可以基于初等函数进行；对于后一种情况，我们必须求助于数值积分。

现在，我们将这个例程应用到一些简单的函数。考虑函数f(x) = x,视为位于区间-π < x < π之上的周期函数；其曲线图具有图93所示的锯齿形状(saw-tooth)。因为这个函数是一个奇函数(即，f(-x) = - f(x))，第一个欧拉方程中的被积函数是奇函数；由于积分极限关于原点对称，因此对于所有 m = 0, 1 ,2 , ... 所得积分将为零，因此，所有的 $a_0$ 项是0，我们这个级数将仅由正弦项组成，对于 $b_m$ 我们有

$b_m = \frac{1}{\pi}\int_{-\pi}^{\pi}xsin(mx)dx = \frac{2}{\pi}\int_{0}^{\pi}xsin(max)dx$

分部积分法(integration by parts)导出

$b_m =\frac{2{(-1)}^{m+1}}{m}$ 。

因此，我们有

$f(x) = 2(\frac{sin(x)}{1} - \frac{sin(2x)}{2}+ \frac{sin(3x)}{3} -+ ...)$ 。-------------------------------------------(7)

图 94 显示了该系列的前四个部分和；我们清楚地看到正弦波是如何在±π附近堆积的，但是对于区间的每个点，包括在±nπ处的不连续点，该级数最终收敛到图93的锯齿图并不那么明显。事实上，在Fourier时代，平滑正弦波的无限和可能会收敛于一个其图形一点也不平滑的函数这一事实遭到了极大的怀疑。[6] 但2000年前的Zeno悖论也是如此！当谈及无限过程时，我们总是可以期待一些惊喜即将到来。

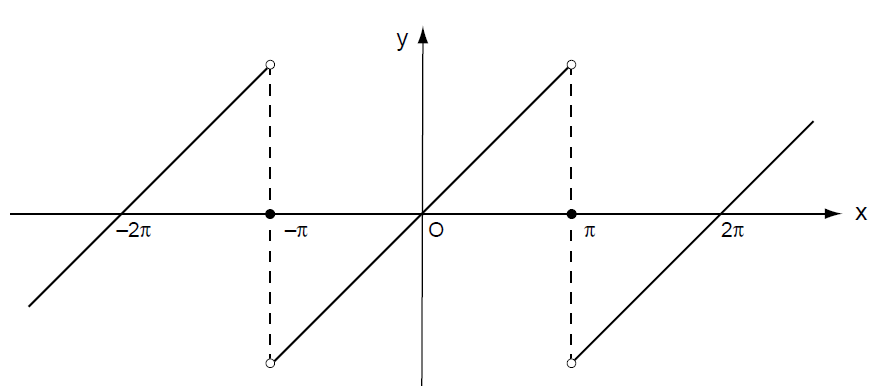
--------------图93 周期函数f(x) = x(-π < x < π)的函数图像--------------------

-----图94 周期函数f(x) = x(-π < x < π)的Fourier展开式的前4项和的函数图像-----

因为等式(7)对于任意x值都成立，我们不妨代入一些具体的值。代入x = π/2,我们得到

$\frac{\pi}{2} = 2(1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} +- ...)$ 。

等式两边分别除以2便得到Gregory-Leibniz级数(第159页)。代入x = π/4,经过一些步骤之后，我们得到

$\frac{\pi \sqrt{2}}{4} = 2(1 + \frac{1}{3} - \frac{1}{5} - \frac{1}{7} ++-- ...)$ ，

一个鲜为人知的公式，将奇数整数的倒数(reciprocals)与 π 和 $\sqrt{2}$ 连接起来(请注意，该级数的右侧与Gregory-Leibniz级数具有相同的项，但它们的符号每两项出现交替)。

对偶数函数 $f(x) = x^{2}$ (再次地，视为区间 -π < x < π 上的周期函数)，经过两次分部积分后，我们得到一个仅由余弦项组成的Fourier级数：

$f(x) = (\frac{\pi}{3})^{2}- 4(\frac{cos(x)}{1^2} -\frac{cos(2x)}{2^2} + \frac{cos(3x)}{3^2} -+ ... )$ 。----------------------------------(8)

代入 x = π并化简得到结果

$\frac{\pi^2}{6} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + ...$ 。

这是Euler在 1734 年以完全不同且不严格的方式发现的著名公式(见第12章)。类似的方法可以得到很多其他的级数，如图95所示。

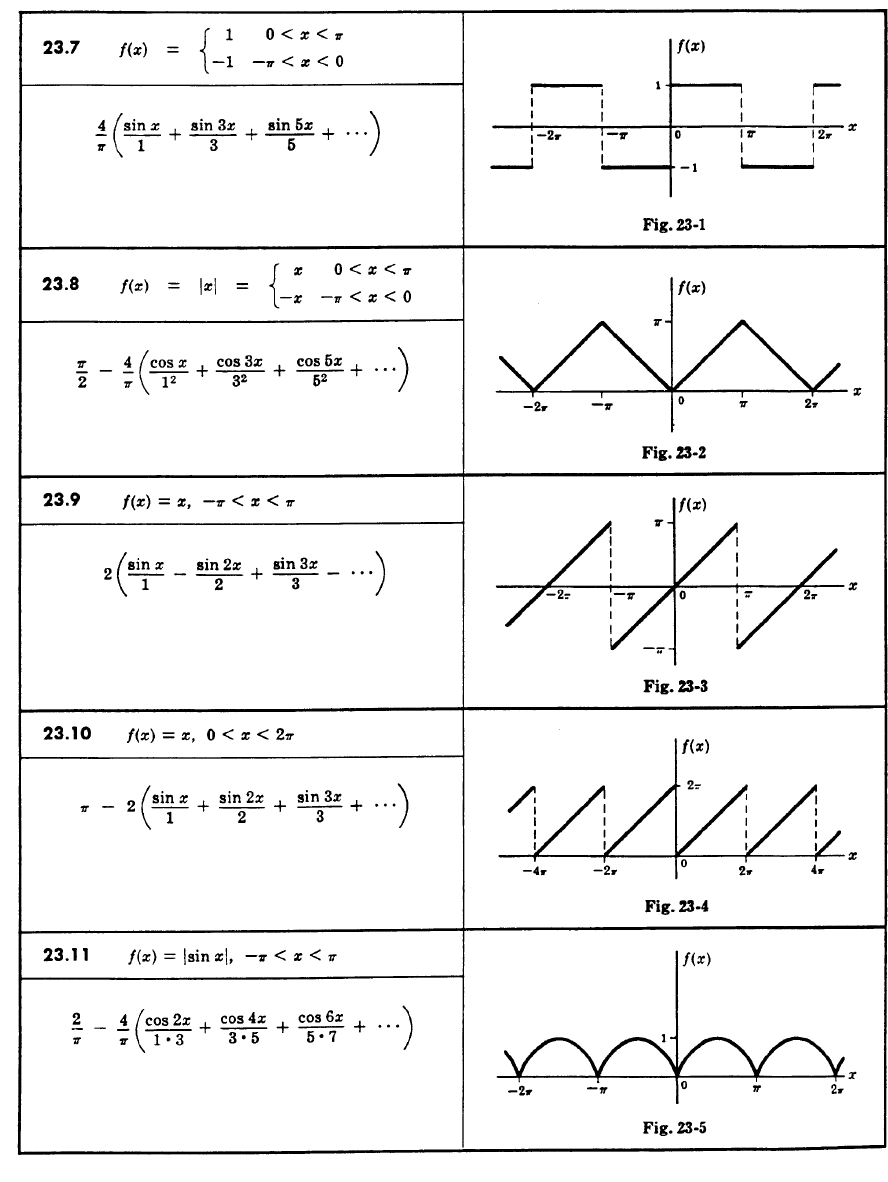
---------------------图95 一些初等函数的Fourier展开式------------------------

我们已经为周期为 2π的函数制定了Fourier定理公式，但可以通过代入 x’ = $\frac{2\pi}{P}$ 轻易地调整为具有任意周期P的函数。则使得根据角频率(angular frequency)ω(omega)(定义为 $\frac{2\pi}{P}$ ) 来公式化Fourier定理就变得更为方便。则，Fourier定理表达的数学思想是，任意周期函数都可以写成角频率为ω, 2ω, 3ω, 等等的无穷多项正弦函数和余弦函数的和。这些频率中的最小频率(即，ω)是基础频频率或基频(fundamental frequency)，而其更高的倍频称为谐波(harmonics)。

当然，“harmonic”这个词来自音乐，因此，我们暂时离题(digress)一下，进入到声学的世界。乐音(a musical sound)——音调(a tone)——是由物质体(如小提琴弦(a violin string)或长笛的气柱(the air column of a flute))有规律的(regular)、周期性的振动(periodic vibrations)产生的。 这些有规律的振动会在耳朵中产生一种音高感(a sense of pitch)(pitch——音高，音符的高低度)，可以将其写为乐谱上的音符(musical staff)。相比之下，非音乐性的声音——噪音(noises)——是不规则、随机振动的结果，它们通常缺乏音高感。那么，音乐就是周期性振动的范畴(realm)。[7]

乐音的音高由其振动频率决定：频率越高，音调越高。例如，音符(note) C(五线谱上的“中央C”)对应264赫兹(hertz)的频率，或周期每秒；音符 A 高于 C，达到440赫兹，音符C’ 高于C一个八度音阶(octave)，达到528赫兹。[8]音程(Musical intervals)对应频率比率(ratios)：一个八度音阶对应的比率为 2:1，五度音阶对应3:2，四度音阶对应4:33，依此类推(名称“八度音阶”、“五度音阶”和“四度音阶”源自这些音程在音阶(musical scale)中的位置)。

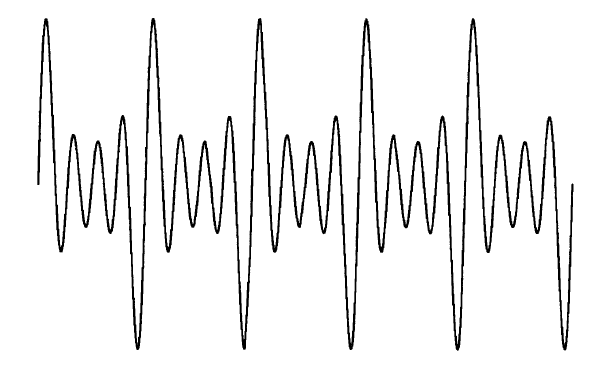
-----------------------------图96 一段音乐音调的声波图------------------------

这个最简单的乐音(musical tone)是纯音(pure tone)；它是由正弦波产生的，或者——用一个物理学术语来说——由简单的谐振动(simple harmonic motion)(注：谐，用另一个字解释，就是“詥(hé)”,言合(说话合得来，合众意，合众意那自然就顺，就和气，表达的就是这个意思)，就是和洽(和睦融洽)；体现在声音中，就是悦耳的声音，相对于读噪声而言。)产生的。[9] 纯音可以由电子合成器(electronic synthesizer)产生，但所有乐器产生的自然音调的波形图(wave profiles)虽然是周期性的，但相当复杂(图 96)。然而，根据Fourier定理，这些音调总是可以分解成它们的简单正弦分量——它们的分音(partial tones)。那么，音乐音调是复合音调(compound tones)，其组成正弦波是基频(最低)频率的谐波(这些波的频率总是基频率的整数倍)。[10]

乐音的谐波不仅仅是数学抽象：训练有素的耳朵实际上可以听到它们。事实上，正是这些谐波赋予了音调特有的“色彩(color)”——它的音乐质感(musical texture)。(风琴的)小号(trumpet)之所以能发出美妙的声音，是因为它含有丰富的和声(rich harmonic content)；长笛的声音谐波差，因此“色彩圆润(mellow)(图97)。每种乐器都有其特有的声谱(acoustic spectrum)——谐波成分的特征。令人惊奇的是，人耳可以将复合音分解成其组成的纯音，并分别听到每个纯音，就像棱镜将白光分解成彩虹色(“频谱(spectrum)”的名称由此而来)。 耳朵实际上是一个Fourier分析仪。[11]

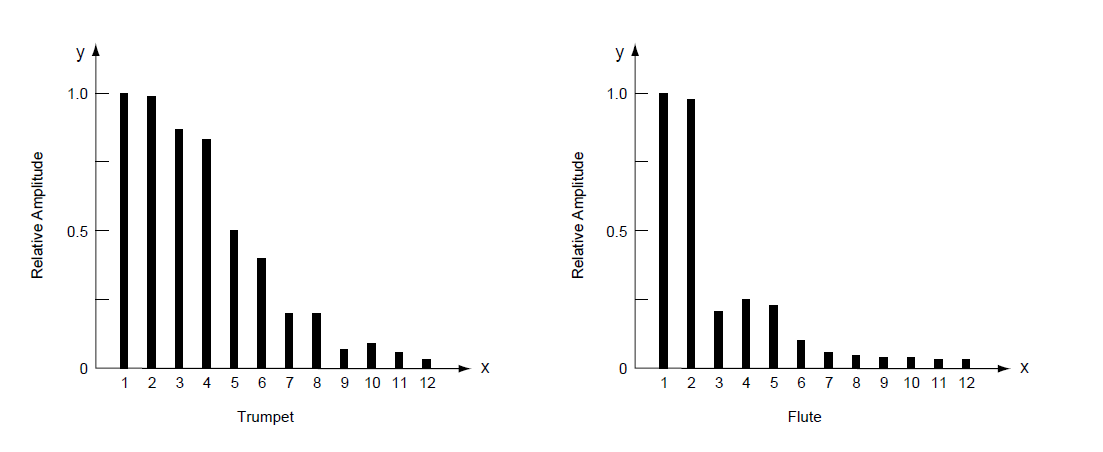
------------------------图97 小号(左)和长笛(右)的声谱波形图-------------------

在19世纪，这些想法是新奇的：科学家和音乐家发现很难相信一个音调实际上是其所有谐波分量的代数和。伟大的德国物理学家和生理学家赫尔曼·路德维希·费迪南德·冯·亥姆霍兹(Herman Ludwig Ferdinand von Helmholtz, 1821-1894)通过使用谐振器(Resonator)证明了分音(partial tones)的存在——谐振器是各种尺寸的小玻璃球，每个都能增强复合音中的一个特定频率(图98)。一系列这样的谐振器形成了一个类似于人耳的原始Fourier分析仪。Helmholtz也做了相反的事情：通过组合不同频率和振幅的不同简单音调，他能够模仿实际乐器的声音，预见了现代电子合成器。

------------------------图98 谐振器(Resonator)--------------------------------

当我们在乐谱中写下谐波集 1，2，3，...，我们得到图 99 所示的音符序列，在音乐理论中，它起着至关重要的作用：正是从这个序列中得出了基本的音程。[12] 这个序列应该与数学级数 1 + 1/2 + 1/3 + ...同名，这并非巧合：后者的项正好是前面项的谐波周期。此外，级数1 + 1/2 + 1/3 + ...的每一项恰好是其前后两项的谐波均值(harmonic mean) (即前后两项的倒数的算术平均值的倒数)[13]。这些只是“谐波”一词在数学中多次出现的两个例子，反映了人类思想的这两个伟大创造之间的密切联系。

------------------------图99 谐波级数(The harmonic series)---------------------

当然，Fourier定理的重要性不仅限于音乐：它是所有周期现象的核心。 Fourier自己将定理扩展到非周期函数，将它们视为周期函数的极限情况，其周期接近无穷大。然后，Fourier级数被表示在所有频率上的正弦波的连续分布的积分所取代。事实证明，这个想法对本世纪初量子力学的发展具有极其重要的意义。Fourier积分的数学比级数复杂，但其核心是构成所有三角学支柱的两个相同函数：正弦和余弦。

注释和资料来源：

1. 没有Fourier的英语版传记。在Eric Temple Bell 的著作<<Men of Mathematics>>(数学人)(Harmondsworth,U.K.: Penguin Books, 1965年)的第1卷第12章有一段Fourier的简短生平描写。本章中Fourier的传记描写部分基于Jerome R. Ravetz和I. Grattan-Guiness在DSB(Dictionary of Scientific Biography)中关于Fourier的文章。

2. 通过“合理的行为”指的是函数f(x)在区间-π < x < π上是分段平滑的(sectionally smooth),即，除了可能在有限数量的有限跳跃不连续处之外，它在那里是连续且可微的。在跳跃不连续点处，我们定义f(x)为 $\frac{f(x^-)+f(x^+)}{2}$

，也就是说，f(x)的值之间的平均值就在所讨论的点的左侧和右侧。关于完整的讨论，参见Richard Courant的著作<< Differential and Integral Calculus>>(微积分)( London: Blackie & Son, 1956年版)之第1卷第9章。

3. 在注释 2 规定的条件下保证收敛。

4. 这种情况可以类比于函数f(x)以幂级数 $\sum_{i=0}^{n}a_ix^i$ : 我们必须确定系数，以便其和将逼近收敛区间中每个点的函数。

5. 在注释 2 中提到的条件下，逐项积分是允许的。

6. 对于与此问题相关的有趣历史事件(episode),参见Paul J. Nahin所著的<<The Science of Radio>>(无线电科学)( Woodbury, N.Y.: American Institute of Physics, 1995)第85-86页。

7. 然而，在我们这个时代，这种传统的区别几乎消失了：见证古典音乐鉴赏家和摇滚乐迷之间关于什么是“真正的”音乐的永无止境的争论。

8. 这些频率符合称为音乐音高(concert pitch)的国际标准，其中A = 440 赫兹。科学音高(Scientific pitch)基于C = 256赫兹，其优点是 C的所有八度音阶都对应于2的幂；在这个音调中，A = 426:7 赫兹。

9. 术语“纯音(pure tone)”指的是正弦和余弦振动。这是因为人耳对音调的相对相位不敏感；即，sin(ωt)和sin(ωt + ε)的声音对耳朵来讲听起来感觉都一样。

10. 严格来说，泛音(overtones)(音调中存在任何一组较高频)与谐音(harmonics)(其频率是基频的整数倍)之间存在区别。大多数乐器都会产生谐波泛音，但有些乐器(尤其是鼓和打击乐器)具有非谐波成分，导致它们的音高不太明确(有杂音)。

11. 相比之下，眼睛没有这种能力：当蓝光和黄光叠加时，结果显示为绿色。

12. 然而，存在两种不同的比例，9:8 和 10:9，因为当旋律从一个音阶移调(转换)到另一个音阶时，整个音调会造成困难。出于这个原因，所有现代乐器都根据等律音阶调音，其中八度音阶由十二个相等的半音组成，每个半音具有频率比 $\sqrt[12]{2}:1$ 。这个数的比率值约为1.059,正好略为小于语调半音16:15 = 1.066。参见我的文章“What is there so Mathematical about Music(音乐中有什么数学？)”，数学教师报(Mathematics Teacher)，1979年9月，第415-422页。

13. 两个正整数a和b的谐波均值H 定义为 $\frac{2ab}{a+b}$ , 从这个公式可以推出， $\frac{1}{H }= (\frac{1}{a} + \frac{1}{b})/2$ ，即，谐波均值的倒数是a和b各自倒数的算术均值。例如， $\frac{1}{2}$ 和 $\frac{1}{4}$ 的谐波均值是 $\frac{1}{3}$ 。

14. 傅里叶级数也被推广到具有类似于正弦和余弦的正交关系的非三角函数。有关详细信息，请参阅有关高等应用数学的任何教材。

内容来源：

<<Trigonometric Delights>> 作者：Eli Maor

$\frac{1}{3}$

互联网公司哪个部门负责网站建设/在线培训系统平台

相关文章：

趣味三角——第15章——傅里叶定理

市场营销的核心是什么？

c/cpp - 多线程/进程多进程

MySQL必知必会 | 存储过程、游标、触发器

优化Facebook广告ROI的数据驱动方法：从投放到运营

动态规划入门经典问题讲解

快速入门深度学习1（用时1h）

PaddleOCR关键信息抽取(KIE)的训练(SER训练和RE训练)错误汇总

信息收集之搜索引擎

Flutter（四）布局类组件

【黑马】Java基础从入门到起飞目录合集

PMP考前冲刺3.10 | 2023新征程，一举拿证

JavaScript Math常用方法

【C++】模板进阶

三板斧解决leetcode的链表题

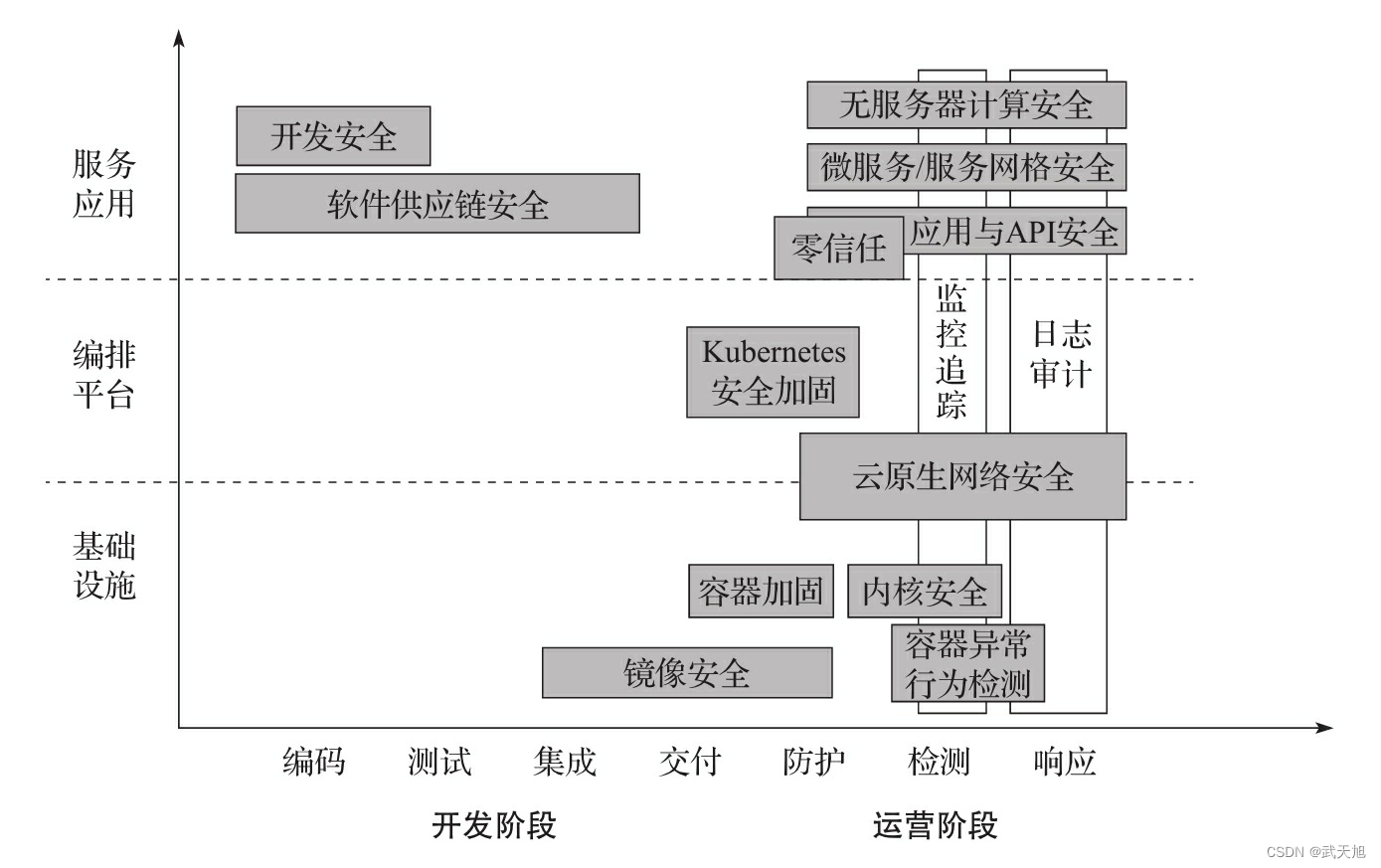
全生命周期的云原生安全框架

【本地网站上线】ubuntu搭建web站点，并内网穿透发布公网访问

电脑怎么重装系统？教你轻松掌握这些方法

leetcode-每日一题-2379(简单,字符串)

SLF4J日志框架在项目中使用

Spark MLlib 模型训练

Python中变量的作用域精讲

数据仓库工程师的工作职责的相关介绍

ESP UART 介绍

第十三届蓝桥杯省赛Python大学B组复盘

linux入门---vim的配置

Python简写操作（for、if简写、匿名函数）

毕业设计常用模块之温湿度模块DHT11模块使用

Cadence Allegro 导出Design Rules Net Shorts Check（DRC）Report报告详解

第 46 届世界技能大赛浙江省选拔赛“网络安全“项目C模块任务书