决策树Decision Tree
目录
- 一、介绍
- 发展
- 优点
- 缺点
- 基本原理
- 二、熵
- 1、熵
- 2、条件熵
- 3、信息增益
- 4、信息增益率
- 三、基尼系数
- 四、ID3算法
- 1、建树过程
- 2、优点
- 3、缺点
- 五、C4.5
- 1、二分法处理连续变量
- 1、流程:
- 2、示例
- 2、缺点
- 六、CART
- 1、连续数据处理
- 2、离散数据处理
- 3、CART回归原理
- 1、均方误差
- 2、示例
- 4、缺失值
- 5、CART建树原理总结
- 七、剪枝
- 1、前剪枝
- 2、后剪枝
- 八、分类模型评估指标
- 1、判别模型
- 1、混淆矩阵
- 2、ROC
- 3、PR
- 2、排序模型
- 1、K-S
- 2、GINI系数
- 九、交叉验证&&参数搜索
- 1、交叉验证
- 2、网格搜索
- 3、随机搜索
- 4、贝叶斯搜索
- 5、参数搜索总结
- 十、反欺诈示例
- 1、读取数据集
- 2、查看数据集情况
- 3、拆分数据集
- 4、建立决策树模型
- 5、使用网格搜索优化模型
- 6、使用随机搜索优化模型
- 7、使用贝叶斯搜索优化模型
- 8、决策树可视化
- 9、模型预测及评估指标
- 1、模型预测
- 2、绘制评估指标
- 十一、使用pyspark实现
- 1、读取数据
- 2、数据向量化
- 3、切分数据集
- 4、创建和训练决策树模型
- 5、模型预测、评估
- 6、关闭资源
一、介绍
决策树说一种常用的机器学习算法,它可以用于分类和回归问题。它通过一系列的判断条件对数据进行分类,最终形成一个树形结构。

发展

优点
-
易于理解和解释:非常直观地展示每个决策逻辑。
-
可处理各种数据:可以处理数字和类别数据,也可以处理缺失值和异常值。
-
自动特征选择:构建时,会自动进行特征选择,可以帮助找出哪些特征对决策影响最大。
-
灵活性,可与其他机器学习模型结合,形成强大的集成模型,如随机森林。
-
模拟人类决策过程
缺点
- 容易过拟合:当模型复杂度较高或训练数据较少时,需要进行剪枝等操作。
- 对噪声和异常值敏感:可能会导致模型的不稳定性。
- 不适用于高维数据:因为在高维空间中,决策树算法很难找到合适的划分点。
- 不能处理连续型输出变量:决策树算法不能直接处理连续型输出变量,需要进行离散化等操作。
基本原理
决策树是一个分层组织结构,每个节点根据特征值将数据空间分割成若干部分。

对空间进行划分的核心问题有两个:
- 在哪个轴(自变量)上做分割
- 在轴(自变量)上的哪个点做分割
为了提高计算效率,决策树采用了贪婪算法对空间进行分割,即在当前空间(树节点)中,将划分正负效果最好的自变量作为下一步划分的优先选择,而该自变量上划分正负例最好的点是分割点。
决策树会对自变量x的每个取值进行遍历,并在每个取值上计算划分后的空间样本纯净度。样本越纯净,分割效果越好。
量化决策树选择特征时的重要程度指标主要分为2大类:
- 熵
- 基尼不纯度
二、熵
1、熵
熵是由香农提出,用来描述混乱程度的指标。熵越大,每个类别的占比越接近,样本越混乱;熵越小,每个类别的占比差异越大,样本越纯净。
信息熵计算公式:
Info(D) = -Σ(p(i) * log2(p(i)))
2、条件熵
引入某一个自变量后,观察对因变量的影响,即为条件熵。
对于数据集D,考虑特征A,求它的信息条件熵。
info(Dj):对Dj的数据集的熵
|Dj|中的Dj:表示数据集D被A这样的自变量的i个水平切割之后样本的数量
|D|:表示样本所有数量

举例计算

目标变量是buys_computer,这里加入自变量age,计算buys_computer的条件熵:
首先判断age的水平,有三个:小于等于30、31~40、大于40
信息熵:Info(age≤30) = -( 2/5 * log2(2/5) + 3/5 * log2(3/5)) 备注:log2中2为底数
条件熵:Info(buys_computer | age≤30) = 5/14 * Info(age≤30)
同理:
Info(buys_computer | 30<age<40) = 4/14 * Info(30<age<40)
Info(buys_computer | 40<age) = 5/14 * Info(30<age<40)
Info(buys_computer | age) = Info(buys_computer | age≤30) + Info(buys_computer | 40<age) + Info(buys_computer | 40<age) = 0.694
3、信息增益
计算公式:信息增益 = 熵 - 条件熵,如图所示

信息增益代表引入变量A之后,随机变量D混乱程度或纯净程度的变化。如果变化越大,说明特征影响越大,特征越重要。
一个样本按照特征A被切为多个部分后,信息熵会下降(严格来说是不增的),下降得越多,说明切分效果越好。
信息增益是用于度量切分前后信息熵变化的指标,信息增益越大,意味着切分效果越好。
分别计算age、income、student、credit_rating自变量的信息增益:
Info(buys_computer) = - ( 9/14log2(9/14) + 5/14log2(5/14) ) = 0.940
Gain(age) = Info(buys_computer) - P(buys_computer | age) = 0.940 - 0.694 = 0.246
同理:
Gain(income) = 0.029
Gain(student) = 0.151
Gain(credit_rating) = 0.048
4、信息增益率
信息增益率在信息增益的基础上,除以相应自变量信息熵
公式:

对特征A求信息增益率,特征A的信息增益 /
图中SplitInfo公式:分子|Dj|为 特征A在D的j个水平的数量,分子|D|为总样本数量
SplitInfo衡量了特征的熵(特征的分类水平数量越多,该值越大)
用它对信息增益进行调整,可以减少分类水平数量的差异导致的模型选择分类变量时的偏差。
计算SplitInfo和age的信息增益率:
SplitInfo age(D) = - 5/14log2(5/14) - 4/14log2(4/14)- 5/14*log2(5/14)= 1.577 备注:age为公式中的A
GainRate(age) = Gain(age) / SplitInfo age(D) = 0.246 / 1.577 = 0.156
三、基尼系数
与熵相反,基尼系数越小,差异越大。
计算公式

与信息熵类似,当树节点中不同类别的样本比例一致时(P1=P2=…=Pm),基尼系数最高。
参考条件熵的概念,按照特征A进行分裂后的基尼系数定义为:

这是按照特征A分裂后,各子节点的基尼系数加权和,权重为每个子节点的样本量中父节点的比例。
仍计算样本及age变量的基尼系数:
Gini(D) = 1 - [ ( 9/14 )2 + (5/14)2 ] = 0.549 备注:2表示平方
Gini age(D) = 5/14[ 1- (2/5)2 - (3/5)2 ] +
4/14[ 1- (0/4)2 - (4/4)2 ] +
5/14[ 1- (3/5)2 - (2/5)2 ] = 0.343
四、ID3算法
用信息增益作为节点分裂条件的算法。
1、建树过程
仍用电脑销售数据为例:
Gain(age) = 0.246
Gain(income) = 0.029
Gain(student) = 0.151
Gain(credit_rating) = 0.048
根据信息增益,自变量age的信息增益值最大,所以第一层决策树应该为age,切分水平分别为≤30、31~40、>40

然后在第一层决策树的各个节点上,重新计算各变量的信息增益,然后筛选出最重要的变量,以此为根据建立第二层决策树,划分情况如下:

决策树的规则集:

2、优点
- 易解释,可以生成可视化的决策过程。
- 可以处理离散特征和连续特征。
- 可以处理多类别问题。
- 在一定条件下,对缺失值和异常值具有较好的容忍性。
3、缺点
- 无剪枝策略,容易过拟合,产生复杂的树结构;
- 对于包含大量特征和类别的数据集,决策树可能过于复杂,导致计算和存储开销增加;
- 强调信息增益倾向于选择具有更多水平特征的值,导致结果不准确;
- 没有考虑缺失值,存在缺失值时,无法使用;
- 特征分类很多时,信息增益可能导致偏差;
- 只能用于分类。
五、C4.5
C4.5算法在继承ID3算法思路的基础上,将首要变量筛选的指标由信息增益改为信息增益率,信息增益率最大的特征作为划分特征,并加入了对连续变量的处理方法。
C4.5克服了ID3的几个缺点:
- 用信息增益选择属性时偏向于选择分枝比较多的属性值,即取值多的属性;
- 不难处理连续性数据;
- 可以处理缺失值:通过概率权重的方法来处理。
1、二分法处理连续变量
1、流程:
- 将所有数据样本按照属性feature的值由小到大进行排列,得到属性feature的取值序列(x1,x2,…,xn)
- 在序列(x1,x2,…,xn)中一共有N-1种二分方法,共产生N-1个分割阈值。例如,对于第i种二分方法,其二分阈值为: (xi + x(i+1) ) /2 ,此阈值将数据集划分为2个字数据集(x1,x2,…,xi),(xi+1,…xn),由此可以计算二分方法之后的信息增益。
- 分别计算N-1种二分方法下的信息增益,选取信息增益最大的二分结果作为对属性feature的划分结果,并记录此时的二分阈值。
2、示例

Info(D) = -3/5 * log2(3/5) - 2/5 * log2(2/5) = 0.971
年收入从小到大排列:70,95,100,120,125
中值T: 82.5,97.5,110,122.5
T = 82时:
Info(T>82.5) = -3/4 * log2(3/4) - 1/4 * log2(1/4) = 0.8113
Info(T<82.5) = -log2(1/1) = 0
Gain(T=82.5) = 0.971 - (4/5 * 0.8113 + 1/5 * 0 ) = 0.32

T = 97.5时
Info(T>97.5) = -3/3 * log2(3/3) = 0
Info(T<97.5) = -2/2 * log2(2/2) = 0
Gain(T=97.5) = 0.971 - (3/5 * 0 + 2/5 * 0) = 0.971
选择信息增益最大的划分点进行划分。

2、缺点
- C4.5决策树算法一种多叉树,运算速度慢;
- C4.5决策树算法使用熵模型作为特征选择,需要大量的对数运算;
- C4.5决策树算法在构造树的过程中,对数值属性需要按照大小进行排序,从中选择一个分割点,所以只适合能够驻留于内存的数据集,对训练集大的无法在内存中储存时,程序无法运行;
- C4.5决策树算法只能用于分类。
六、CART
采用基尼系数选择最优分割变量及最优分割点的衡量指标。可用于分类和回归。
1、连续数据处理
- m个样本的连续特征A有m个值,从小到大排列a1,a2,…,am
- CART取相邻两样本值的平均数做划分点,一共有m-1个,其中第i个划分点Ti表示:
Ti = ( a i + a(i+1) ) / 2 - 分别计算以这m-1个点作为二分类时的基尼系数,选择基尼系数最小的点作为该连续特征的二元离散分类点,比如取到的基尼系数最小的点为at,则小于at的值类别为1,大于at的值类别为2,这样就做到了连续特征的离散化。
- 最后选择基尼系数最小的切分点进行切分,方式类似于C4.5。
2、离散数据处理
方法:不停的二分特征
如果有三个类别,CART会考虑把特征A分为A1、A2A3,A1A2、A3,A2、A3A1三种组合,找到基尼系数最小的组合进行划分
3、CART回归原理
- 当使用CART用作回归算法时,采用均方误差(MSE)作为节点分裂依据。均方误差衡量了预测值与真实值之间的差异,均方误差越小,说明模型预测能力越好。
- CART回归树的构建过程与分类树类似。首先遍历每个特征的相邻树均值,用该取值将数据集分成2个部分。然后分别计算两部分数据的均方误差,并求和。最后,选择使得均方误差值和最小的特征及其对应的取值作为最优特征和最优切分点。
- 在构建完整颗树之后,可以对树进行剪枝以避免过拟合。剪枝过程中,会删除一些不重要的节点,以提高模型的泛华能力。
- 在进行预测时,CART回归树会根据测试样本的特征值沿着树结构进行搜索,直到找到对应的叶子节点。叶子节点中包含了许多训练样本的目标值,这些目标值的平均值就是测试样本的预测值。
1、均方误差
均方误差MSE是一种常用的回归模型评估指标,用于衡量预测值与真实值之间的差异,计算公式:

2、示例
假设有一组数据,自变量X为1、2、3、4、5,因变量Y与X相对应,Y值分别为1、2、3、4、5
我们会遍历(1+2)/2=1.5、(2+3)=2.5、(3+4)/2=3.5、(4+5)/2=4.5四个切分点。对于每个切分点,都会用它把数据集分为2部分,并计算这2部分数据的均方误差,最后发现当切分点为2.5时,均方误差最小。
对于第一部分有2个样本,目标值对应的平均值为(1+2)/2=1.5,第一部分的均方误差为((1-1.5)2+(2-1.5)2)/2 = 0.25
对于第二部分有3个样本,目标值对应的平均值为(3+4+5)/3=4,第二部分的均方误差为((3-4)2 +(4-4)2+(5-4)2)/3 = 0.67
最后将2部分均方误差相加,总的均方差为0.25+0.67 = 0.92
这2部分数据对于了CART回归树的2个叶子节点。对于第一个叶子节点,它包含了2个样本的目标值,这些目标值的均值为(1+2)/2=1.5。因此当测试样本落入第一个叶子节点时 ,它的预测值为1.5。
同理对于第二个叶子节点,它包含了三个样本的目标值,这些目标值的均值为(3+4+5)/3=4。因此当测试样本落入第二个叶子节点时 ,它的预测值为4。
4、缺失值
- 在sklearn中,决策树不支持缺失值,因此在使用sklearn的cart决策树算法前,需要先对数据预处理,以填补或删除缺失值。
- 根据业务理解处理缺失值:一般缺失值少于20%时,连续变量可用均值或中位数填补;分类变量不需填补,单算一类即可,或用众数填补。缺失值在20%~80%时填补。另外每个有缺失值的变量可用生成一个指示哑变量,参与建模。缺失值大于80%时,每个缺失值的变量生成一个指示哑变量,参与建模,不使用原始变量。
5、CART建树原理总结
- 易于理解,模型简单,不需要对数据预处理,可以处理连续、离散数据,对缺失值和异常值有很好的容错性;
- 只能建立二叉树;
- 对连续性属性处理方式同C4.5,只不过用GINI系数作为划分属性依据;
- 可用于分类、预测,可以使用均方误差代替基尼系数作为损失函数的计算基础,此时CART用于回归;
- 对于离散型,C4.5理论上有多少个离散值就有多少个分裂节点,但CART生成一颗二叉树,每次分裂只产生2个节点。
七、剪枝
完全生长的决策树虽然预测精度提高了,但会使得决策树的复杂度升高,泛华能力减弱,所以需要剪枝。
1、前剪枝
- 用于控制树的生成规模,控制决策树最大深度;
- 控制树中父节点和子节点的最少样本量或比例。
2、后剪枝
- 删除没有意义的分组;
- 计算节点中目标变量预测精度或误差,综合考虑误差与复杂度进行剪枝。
相对来说,前剪枝用的更多。
八、分类模型评估指标
判别类:给出明确结果,比如是、否
排序类:不需给出明确结论,只需给出0~1之间的分值(概率)
1、判别模型
1、混淆矩阵
accuracy(准确率)
precision(精确率):在所有被分类为正例的样本中,真正上正例的比例
recall(召回率):实际为整理的样本中,被预测为正例的样本比例
F1-score
特异度(specificity):实际为负的样本中有多大概率被预测出来:SP = TN /(FP+TN)


2、ROC
ROC曲线又称接收者操作特征曲线,描述分类预测模型命中和误判率之间的一种图形化方法,以真阳性率TPR(灵敏度)为纵坐标,假阳性率FPR(1-特异度)为横坐标

3、PR
PR曲线和ROC曲线类似,PR曲线是precision和recall的点连成的线。

PR曲线通常用于评估二分类器的性能,特别是在数据不平衡的情况下。数据不平衡指的是正负样本数量相差悬殊。
PR曲线的目的是帮助我们选择最佳阈值,以便在精确率和召回率之间取得平衡。它也可以用来比较不同分类器的性能。
- 如果一个分类器的PR曲线完全位于另一个分类器的PR曲线上方,那么前者的性能优于后者;
- 如果2个分类器的曲线相交,那么它们在不同的精确率/召回率权衡下表现不同;
- PR曲线越靠近右上角,分类器性能越好。
2、排序模型
ROC不再重复说明
1、K-S
K-S统计量用于评价模型对好/坏客户的区分能力,KS值越大,表示模型能够将正负例例率分开的程度越大

2、GINI系数
九、交叉验证&&参数搜索
1、交叉验证
交叉验证(Cross-Validation)是一种用来评估模型泛化能力的方法,方法比较多,主流时K折交叉验证,它将数据集分成n个子集,每次使用n-1个子集作为训练数据,剩余的一个子集作为测试数据。这个过程重复n次,每次使用不同的子集作为测试数据,最后计算n次测试的平均性能作为模型的最终性能。
在模型中一般对应的参数为cv,参数类型为int,以三折交叉验证为例:

最后求均值: T = mean( T1 , T2 , T3 )
2、网格搜索
网格搜索(grid search)是一种用来选择模型超参数的方法。它通过遍历超参数的所有可能组合来寻找最优的超参数。通常,网格搜索和交叉验证结合使用,以便在选择超参数时考虑模型的泛化能力。

如图,每个格子都是一组参数,使用交叉验证测试参数效果。但是效率低下。
3、随机搜索
随机搜索(random search)与网格搜索类似,但不是遍历所有可能的超参数组合,而是从超参数空间中随机采样一定数量的组合进行评估。随机搜索的优点是计算成本较低,且在高维超参空间中表现良好,缺点是可能无法找到全局最优解。

4、贝叶斯搜索
- 贝叶斯优化上一种全局优化方法,用于寻找黑盒函数的全局最优解,它通过构建一个概率模型来描述目标函数,并使用这个模型来指导下一步的采样点选择。
- 贝叶斯优化的核心思想上利用贝叶斯定理来更新对目标函数的先验知识。在每一步迭代中,它都会选择一个新的采样点,并使用这个采样点的观测值来更新概率模型。然后它使用一个获取函数来缺点下一个采样点,以便在探索和利用之间取得平衡。贝叶斯优化常用于机器学习的超参数选择,因为它能够在较少的迭代次数内找到全局最优解,并对噪声数据有很好的容错性。
优点: - 贝叶斯调参采用高斯过程,考虑之前的参数信息,不断更新先验
- 迭代次数少,速度快
- 针对凸问题依然稳健

5、参数搜索总结
理论上random search可以更快地将整个参数空间都覆盖到,而不是像grid search一样从局部一点点去搜索。但是grid search和random search,都属于无先验式的搜索,有些地方称之为uninformed search(盲目搜索),即每一步的搜索都不考虑已经探索的点的情况,这也是grid/random search的主要问题,都是“偷懒式搜索”,闭眼乱找一通。
而贝叶斯优化,则是一种informed search(启发式搜索),会利用签名已经搜索过的参数的表现,来推测下一步怎么走会比较好,从而减少搜索空间,提高搜索效率。某种意义上贝叶斯优化和人工调参比较像,因为人工调参也会根据已有的结果及经验来判断下一步如何调参。
十、反欺诈示例
1、读取数据集
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings('ignore')df = pd.read_csv("./data/loan_net.csv")
df.head()

2、查看数据集情况
df.info()
df.describe()

# 因变量情况
df['flag'].value_counts()

# 确定自变量、因变量
label = df.flag.copy()
data = df.iloc[:,:-1].copy()
3、拆分数据集
from sklearn.model_selection import train_test_split
train_data,test_data,train_label,test_label = train_test_split(data,label,test_size=0.4,train_size=0.6,random_state=1234,stratify=label)len(train_data)
len(test_data)
16392/(16392+10929)

4、建立决策树模型
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV,cross_val_score# 初始化决策树分类器
clf = DecisionTreeClassifier(random_state=42)# 交叉验证评估模型性能
cv_score = cross_val_score(clf,train_data,train_label,cv=5,scoring='roc_auc')#查看模型效果
np.mean(cv_score)

5、使用网格搜索优化模型
# 网格搜索
param_grid = {"criterion":['entropy','gini'] , 'max_depth':[2,3,4,5], #'min_samples_split':[2,4,6,8,10], # 停止分裂的最小样本量'min_samples_leaf':[2,4,6,8,10], #停止分裂的叶子节点最小样本量'class_weight':[{0:1,1:1},{0:1,1:2},{0:1,1:3}] #类别的权重
}dtree = DecisionTreeClassifier()
dtree_cv1 = GridSearchCV(estimator=dtree,param_grid=param_grid,scoring='roc_auc',cv=4)
dtree_cv1.fit(train_data,train_label)

最优参数
dtree_cv1.best_params_

最优参数评估效果
dtree_cv1.best_score_

6、使用随机搜索优化模型
# 随机搜索
from sklearn.model_selection import RandomizedSearchCVparam_grid1 = {"criterion":['entropy','gini'] , #'max_depth':np.arange(2,20,step=2), #'min_samples_split':np.arange(2,20,step=2), # 停止分裂的最小样本量'min_samples_leaf':np.arange(2,20,step=2), #停止分裂的叶子节点最小样本量'class_weight':[{0:1,1:1},{0:1,1:2},{0:1,1:3}] #类别的权重
}dtree_RS = RandomizedSearchCV(estimator=dtree,param_distributions=param_grid1,n_iter=100,cv=4,scoring='roc_auc',n_jobs=-1)
dtree_RS.fit(train_data,train_label)

最优参数
dtree_RS.best_params_

最优参数评估
dtree_RS.best_score_

7、使用贝叶斯搜索优化模型
from bayes_opt import BayesianOptimization
def dtree_cv(max_depth,min_samples_split,min_samples_leaf):cvs = cross_val_score(DecisionTreeClassifier(max_depth=int(max_depth),min_samples_split=int(min_samples_split),min_samples_leaf=int(min_samples_leaf),random_state=2),train_data,train_label,scoring='roc_auc',cv=4).mean()return cvs#建立贝叶斯优化对象
dtree_BO = BayesianOptimization(dtree_cv,{'max_depth':(2,10),'min_samples_split':(2,25),'min_samples_leaf':(2,25)}
)#开始优化
dtree_BO.maximize()

# 寻找最大值
dtree_BO.max

8、决策树可视化
# 决策树可视化
import pydotplus
from IPython.display import Image
import sklearn.tree as tree
%matplotlib inline# 获取网格搜索的最优模型
best_tree = dtree_cv1.best_estimator_import pydotplus
# 生成dot文件
dot_data = tree.export_graphviz(best_tree,out_file=None,feature_names=data.columns,max_depth=3,class_names=True,filled=True
)# 用dot文件生成决策树图形
graph = pydotplus.graph_from_dot_data(dot_data)# 如果在Jupyter Notebook中,显示图形
if 'IPython' in globals(): Image(graph.create_png()) # 保存图形为PNG文件
graph.write_png('decision_tree.png')# 显示出决策树
Image(graph.create_png())

9、模型预测及评估指标
1、模型预测
# 利用决策树模型进行预测,并且生成决策树评估指标
from sklearn.metrics import classification_report# 预测值
test_pre = best_tree.predict(test_data)# 计算评估指标
print(classification_report(test_label,test_pre,digits=3))

2、绘制评估指标
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve,average_precision_score,roc_curve,auc# 绘制roc PR KS曲线
def plot_metrics_curve(test_label,train_label,test_pre,train_pre):fpr_test,tpr_test,th_test = roc_curve(test_label,test_pre)fpr_train,tpr_train,th_train = roc_curve(train_label,train_pre)precision_test,recall_test,_ = precision_recall_curve(test_label,test_pre)precision_train,recall_train,_ = precision_recall_curve(train_label,train_pre)# roc curveplt.figure(figsize=[6,6])plt.subplot(221)plt.plot(fpr_test,tpr_test,'b--')plt.plot(fpr_train,tpr_train,'c--')plt.xlabel('fpr')plt.ylabel('tpr')plt.title('roc:test is dotted line')#PR curveplt.subplot(222)plt.plot(recall_test,precision_test,'b--')plt.plot(recall_train,precision_train,'c--')plt.xlabel('recall')plt.ylabel('precision')plt.title('PR:test is dotted line')# KS curve,曲线按阈值降序排列,所以需要1- threshold镜像plt.subplot(212)plt.plot(1-th_test,tpr_test,'b--',label='tpr')plt.plot(1-th_test,fpr_test,'b:',label='fpr')plt.plot(1-th_test,tpr_test-fpr_test,'r-',label='tpr-fpr')plt.xlabel('score')plt.title('KS curve KS=%.2f' %max(tpr_test-fpr_test))
# legend = plt.legend(locals='upper left',shadow=True,frozenset='x-large')plt.tight_layout()plt.show()# print ROC-AUCprint('TestAUC=%.4f,' %auc(fpr_test,tpr_test),'TrainAUC=%.4f' %auc(fpr_train,tpr_train))# print average precision scoreprint('TestAP=%.4f,' %average_precision_score(test_label,test_pre),'TrainAP=%.4f,' %average_precision_score(train_label,train_pre))test_pre = best_tree.predict_proba(test_data)[:,1]
train_pre = best_tree.predict_proba(train_data)[:,1]#绘制评估图形
#使用这个编写的函数绘制评估图形并计算评估指标
#预测概率
test_pre = best_tree.predict_proba(test_data)[:,1]
train_pre = best_tree.predict_proba(train_data)[:,1]plot_metrics_curve(test_label,train_label,test_pre,train_pre)

十一、使用pyspark实现
1、读取数据
from pyspark.sql import SparkSession
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.classification import DecisionTreeClassifier
from pyspark.ml.evaluation import MulticlassClassificationEvaluatorspark = SparkSession.builder.appName("DecisionTreeModel").getOrCreate() # 初始化df=spark.read.csv("./data/dtree/loan_net.csv",header=True,inferSchema=True)
#显示数据
df.show()

2、数据向量化
assembler=VectorAssembler(inputCols=["net_size","degree","average_neighbor_degree","percentage"],outputCol="features"
)
output=assembler.transform(df)
3、切分数据集
train_data,test_data=output.randomSplit([0.7,0.3])
4、创建和训练决策树模型
dt=DecisionTreeClassifier(labelCol="flag",featuresCol="features")
dt_model=dt.fit(train_data)
5、模型预测、评估
#使用测试集进行预测
predictions=dt_model.transform(test_data)
#评估器
evaluator=MulticlassClassificationEvaluator(labelCol="flag",predictionCol="prediction",metricName="f1")
f1_score=evaluator.evaluate(predictions)
print("f1score",f1_score)

6、关闭资源
spark.stop()
相关文章:

决策树Decision Tree
目录 一、介绍发展优点缺点基本原理 二、熵1、熵2、条件熵3、信息增益4、信息增益率 三、基尼系数四、ID3算法1、建树过程2、优点3、缺点 五、C4.51、二分法处理连续变量1、流程:2、示例 2、缺点 六、CART1、连续数据处理2、离散数据处理3、CART回归原理1、均方误差…...
1奇函数偶函数
文章目录 自变量有理化奇偶性周期性初等函数 自变量 自变量是x,这个还挺奇怪,记住就好 y f ( e x 1 ) yf(e^x1) yf(ex1) 里面 e x e^x ex 只算中间变量,自变量是x 做这些题,想到了以前高中的时候做数学题,不够扎实…...
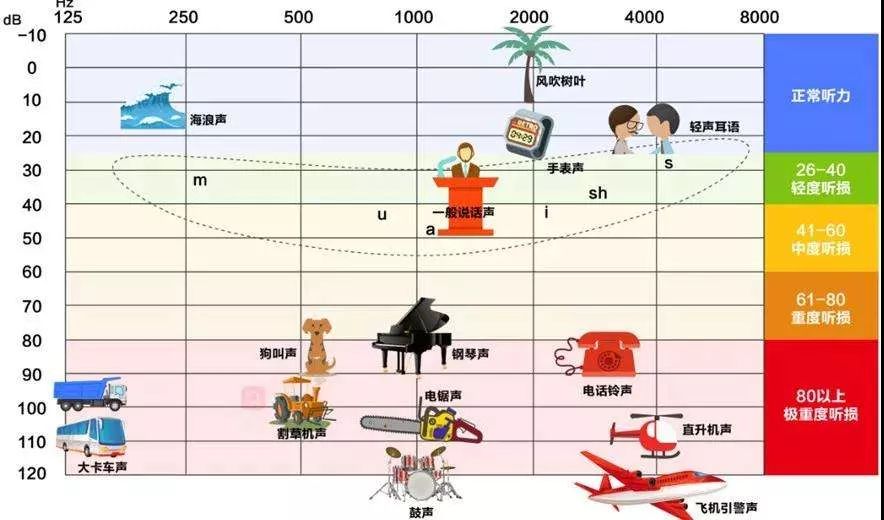
什么情况下需要配戴助听器
以下几种情况需要考虑配戴助听器: 1、听力无波动3个月以上的感音神经性听力障碍。如:先天性听力障碍、老年性听力障碍、噪声性听力障碍、突聋的稳定期等,均可选配合适的助听器。 2、年龄方面。使用助听器没有严格的年龄限制,从出生数周的婴…...
)
Java 基础面试300题 (231-260)
Java 基础面试300题 (231-260) 231 String::toUpperCase是什么类型的方法引用? String::toUpperCase是任意方法引用的示例。它指的是String 类的toUpperCase方法,但不是指任何特定对象。 通常在遍历集合或流时使用。例如&#x…...
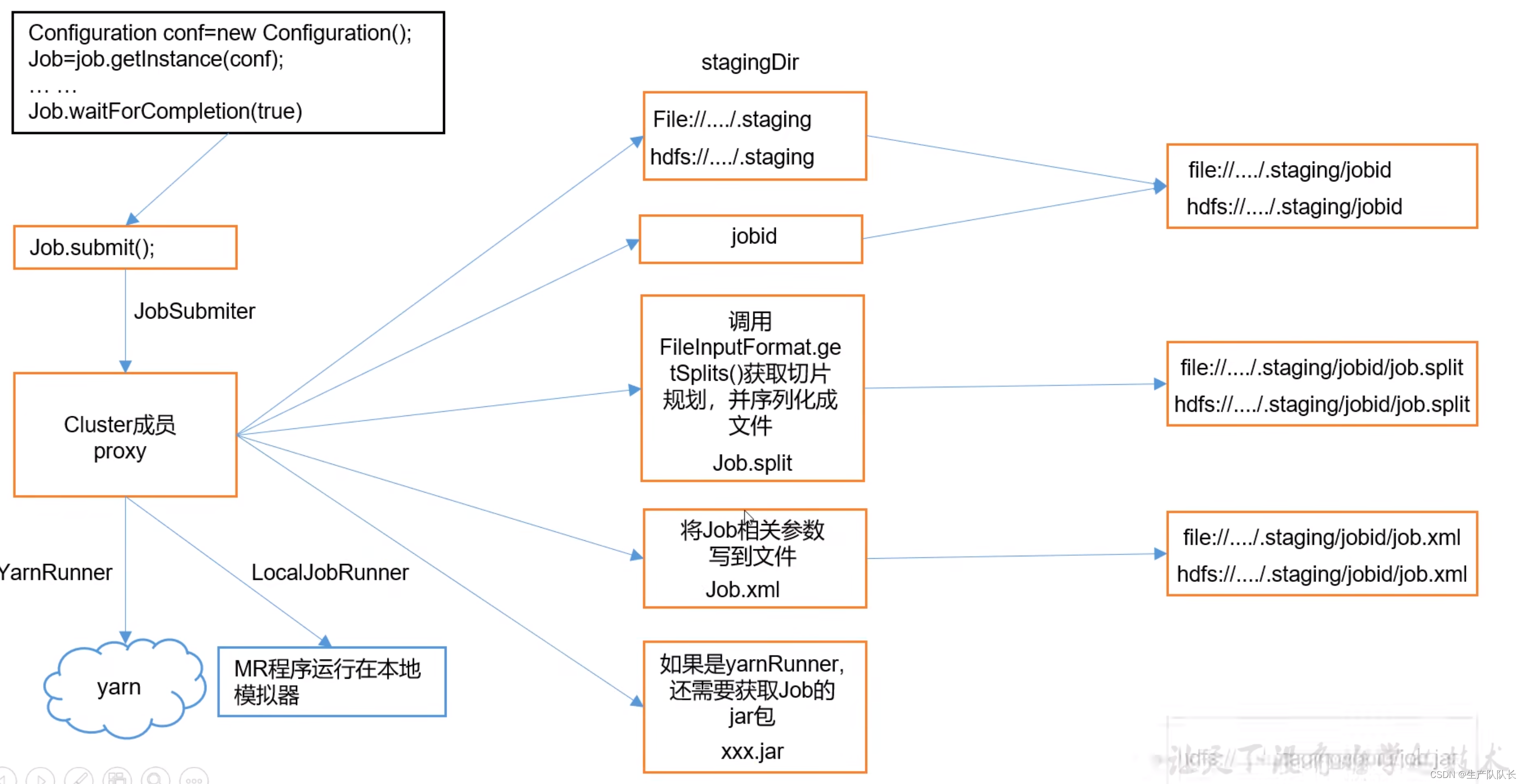
Hadoop3:MapReduce源码解读之Map阶段的Job任务提交流程(1)
3、Job工作机制源码解读 用之前wordcount案例进行源码阅读,debug断点打在Job任务提交时 提交任务前,建立客户单连接 如下图,可以看出,只有两个客户端提供者,一个是YarnClient,一个是LocalClient。 显然&a…...
Linux环境---在线安装MYSQL数据库
Linux环境—在线安装MYSQL数据库 一、使用步骤 1.安装环境 Mysql 驱动 8.0 需要 jdk1.8 才行。 JDK版本:1.8 参考文档 MYSQL版本:8.0.2 下载链接: https://pan.baidu.com/s/1MwXIilSL6EY3OuS7WtpySA?pwdg263 操作系统:CentOS 1.1 建立存…...

git本地配置及IDEA下Git合并部分文件
目录 1、IDEA 下 Git 合并部分文件 2、分支合并忽略特定文件步骤 3、git本地配置 1、IDEA 下 Git 合并部分文件 1.1Git 下存在两个分支,foo 和 bar 分支,想要把 bar 分支上的部分文件合并到 foo 分支: 首先切换到 foo 分支,点击右下角的 …...

安徽京准 NTP时钟同步服务器具体配置方法是什么?
安徽京准 NTP时钟同步服务器具体配置方法是什么? 安徽京准 NTP时钟同步服务器具体配置方法是什么? 可以使用特权终结点 (PEP) 来更新 Azure Stack Hub 中的时间服务器。 使用可解析为两个或更多个 NTP(网络时间协议)服务器 IP 地…...

微信小程序 画布canvas
属性说明 属性类型默认值必填说明最低版本typestring否指定 canvas 类型,支持 2d (2.9.0) 和 webgl (2.7.0)2.7.0canvas-idstring否canvas 组件的唯一标识符,若指定了 type 则无需再指定该属性1.0.0disable-scrollbooleanfalse否当在 canvas 中移动时且…...

leetcode-04-[24]两两交换链表中的节点[19]删除链表的倒数第N个节点[160]相交链表[142]环形链表II
一、[24]两两交换链表中的节点 重点:暂存节点 class Solution {public ListNode swapPairs(ListNode head) {ListNode dummyHeadnew ListNode(-1);dummyHead.nexthead;ListNode predummyHead;//重点:存节点while(pre.next!null&&pre.next.next…...

深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用
Java 18 作为 Java 的最新版本,引入了一系列的新特性和改进,这些变化不仅提升了语言的性能和安全性,也为开发者提供了更多的工具和选项,简化了开发过程,提高了代码的可读性和维护性。本文将深入探讨 Java 18 的主要新特性,分析其设计理念和实际应用,帮助读者理解这些新特…...
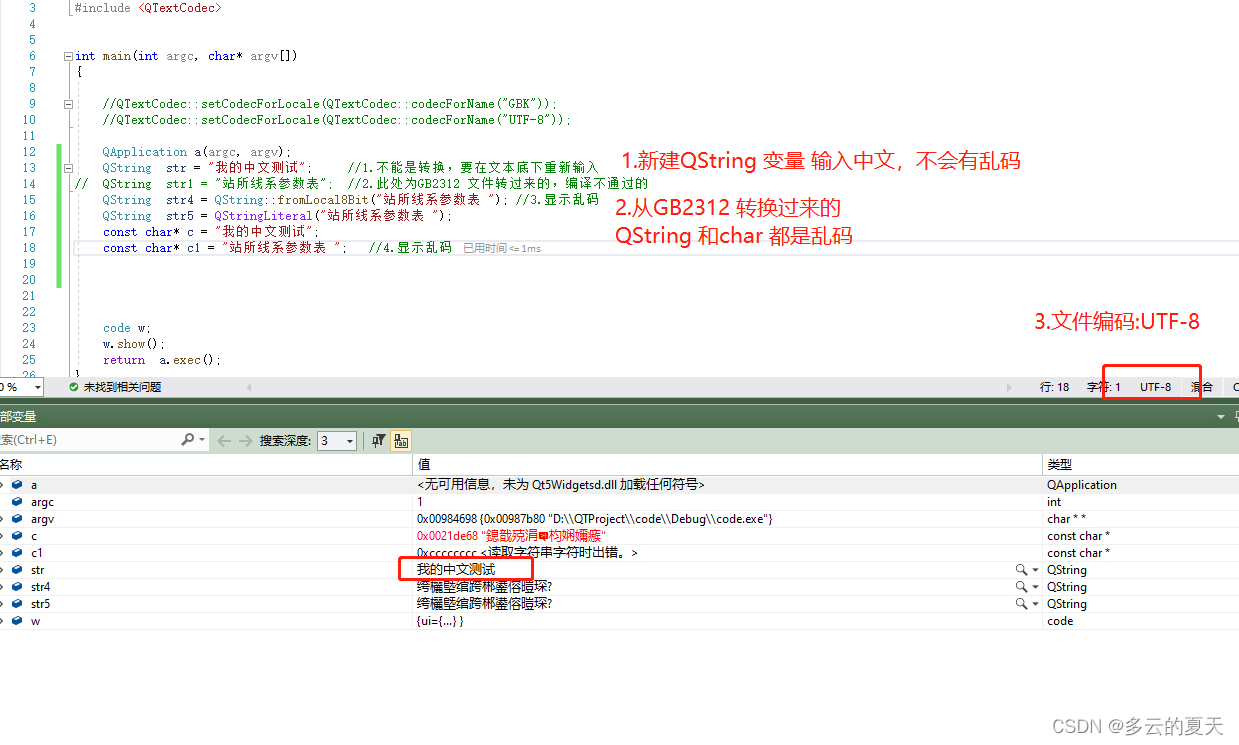
qt4-qt5 升级(2)-GUI-UTF-8-GBK-QTextCode-字符集乱码
MFC与QT的消息机制的区别_qt信号槽机制与mfc的消息映射机制的区别-CSDN博客 1.QT4-QT5差别 kits构建 控件,信号与槽 ui修改好后点击编译会自动生成 ui_XXX.h 聚合的关系,不是拥有的关系。 QWidget 和QWindow有什么差别? 2.VS2019-QT5 构建…...

Qt Designer 生成的 .ui 文件转为 .py 文件并运行
1. 使用使用 PyUIC将 .ui 转 .py (1)打开命令行终端(可以用cmd,或pycharm 下面的 Terminal)。 (2)导航到包含.ui文件的目录。 cd 你的ui文件路径 (3)运行以下命令来…...
Dubbo 3.x源码(20)—Dubbo服务引用源码(3)
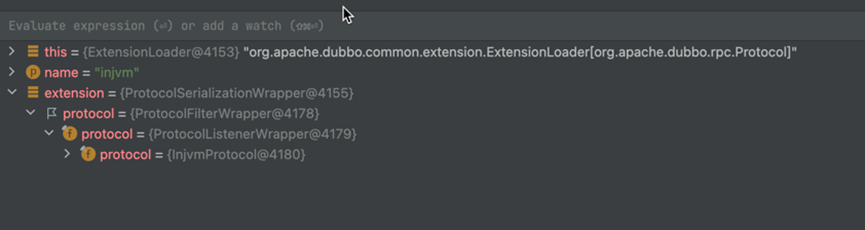
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了调用createProxy方法,根据服务引用参数map创建服务接口代理引用对象的整体流程,我们知道会调用createInvokerForRemote方法创建远程引用Invoker,这是Dubbo …...

开发一个Dapp需要多少?
区块链开发一个Dapp要多少钱? 开发一个去中心化应用(Dapp)的成本取决于多个因素,包括Dapp的复杂性、功能需求、区块链平台以及开发团队的经验水平。以下是一些主要的影响因素: 1. 区块链平台:不同区块链…...
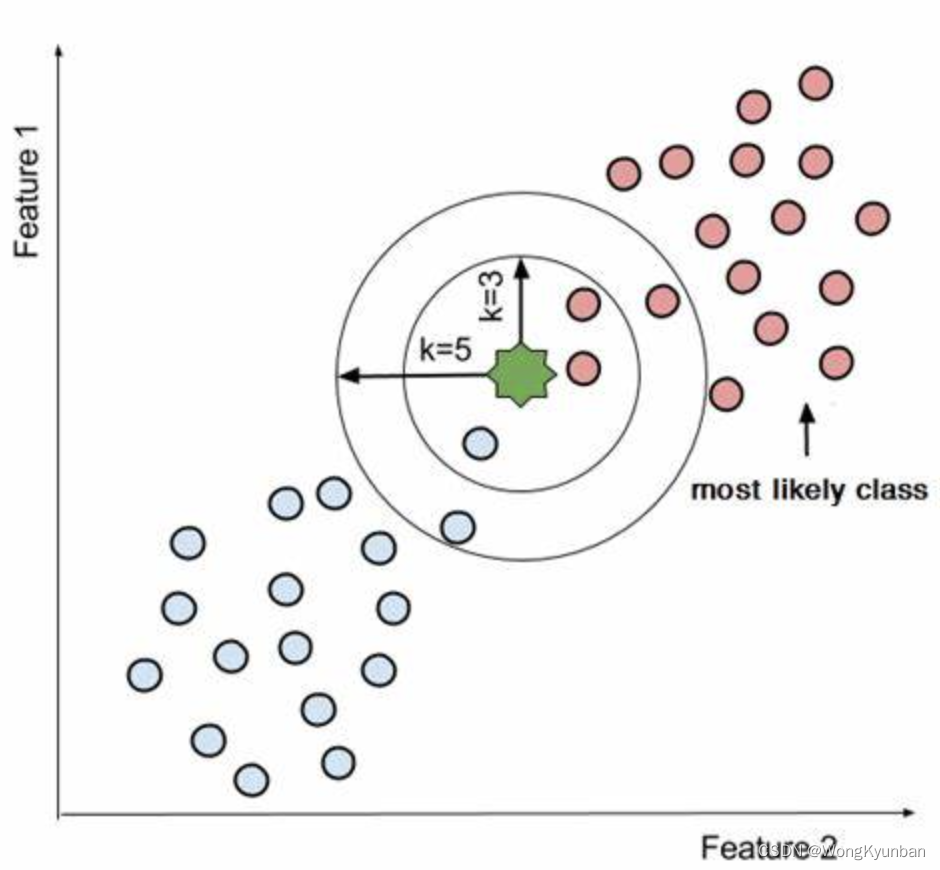
kNN算法-概述
所谓kNN算法就是K-nearest neigbor algorithm。这是似乎是最简单的监督机器学习算法。在训练阶段,kNN算法存储了标签训练样本数据。简单地说,就是调用训练方法时传递给它的标签训练样本会被它存储起来。 kNN算法也叫lazy learning algorithm懒惰学习算法…...

富格林:曝光纠正出金亏损陋习
富格林悉知,虽然现货黄金市场看似变化无常,在操作方向上依旧是有迹可循的,投资者需要了解曝光的专业经验纠正陋习阻止出金亏损。要获得优质的黄金投资出金效果,就需要在明确现货黄金操作技巧的前提下,只有规范遵循已曝…...
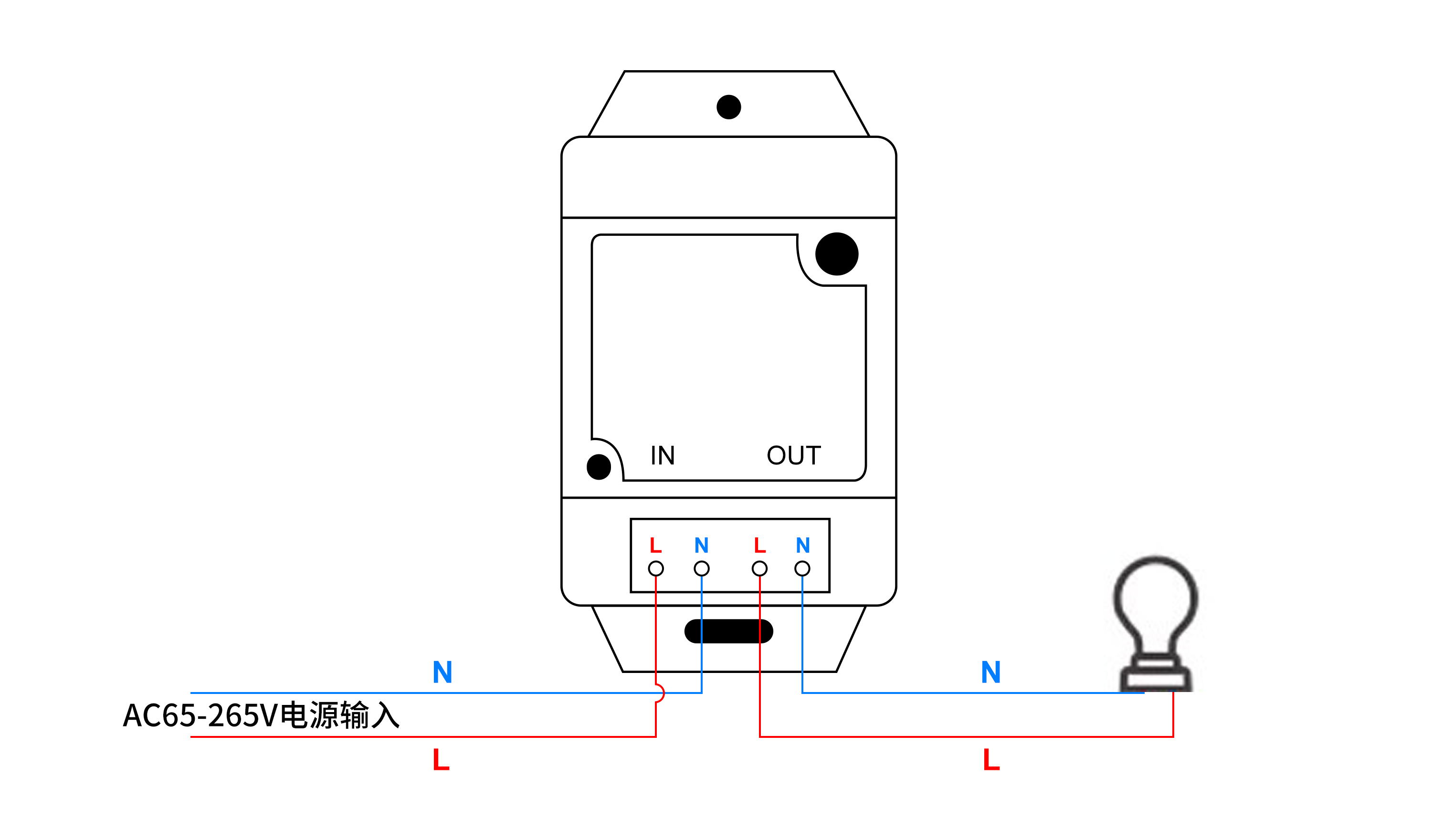
怎么用微信小程序实现远程控制空调
怎么用微信小程序实现远程控制空调呢? 本文描述了使用微信小程序调用HTTP接口,实现控制空调,通过不同规格的通断器,来控制不同功率的空调的电源。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备…...

ES5/ES6 的继承除了写法以外还有什么区别?
一、主要区别 ES5 的继承实质上是先创建子类的实例对象, 然后再将父类的方法添加 到 this 上(Parent.apply(this)) . ES6 的继承机制完全不同, 实质上是先创建父类的实例对象 this(所以必 须先调用父类的 super()方法…...

LeetCode 第401场周赛个人题解
100325. 找出 K 秒后拿着球的孩子 原题链接 100325. 找出 K 秒后拿着球的孩子 思路分析 数据很小,暴力或者数学方法都行 数学方法就是对 n - 1做带余除法,看跑了奇数还是偶数趟,余数如何,确定位置 时间复杂度:O(…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
