【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入
要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点:
- 根节点(Root):树的顶部节点,没有父节点。
- 子节点(Children):每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 叶子节点(Leaf):没有子节点的节点称为叶子节点。
- 父节点(Parent):每个节点都有一个父节点,除了根节点。
- 深度(Depth):从根节点到某个节点的唯一路径的长度,根节点的深度为0。
- 高度(Height):从某个节点到它的最远叶子节点的路径长度,叶子节点的高度为0。
- 遍历(Traversal):遍历二叉树是指按照一定顺序访问树中的每个节点,常见的遍历方式包括前序遍历、中序遍历和后序遍历。
二叉树的应用非常广泛,在后面我会详细介绍。
满二叉树:除了叶子结点外,每个结点都有两个子结点
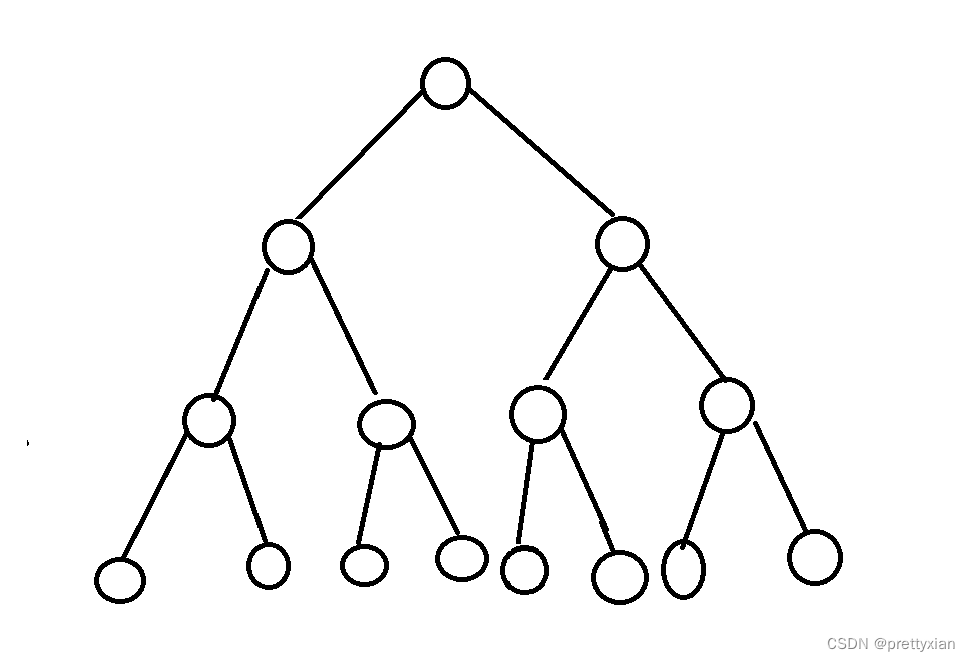
一个深度为k的满二叉树有2的k次方减一个节点。
完全二叉树:除了最底层可能不是满的外,其它每一层从左到右都是满的。
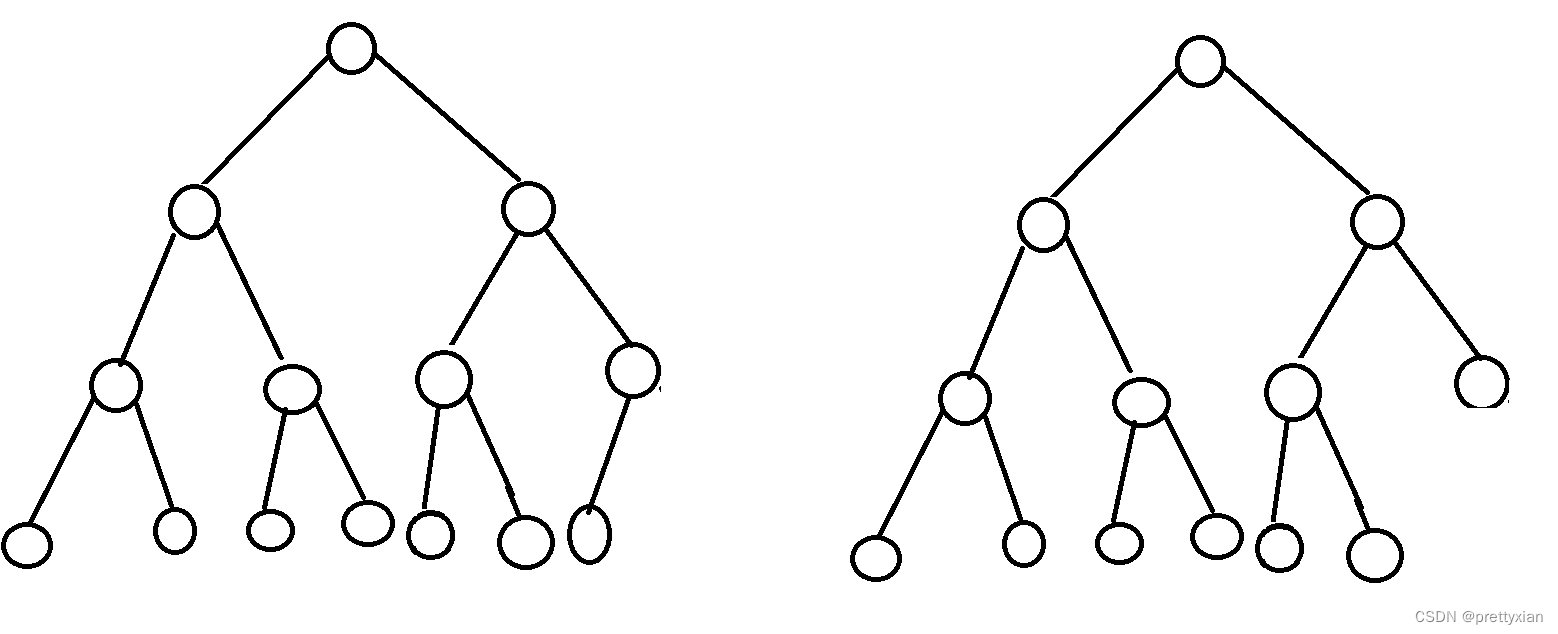
满二叉树是完全二叉树的子集,满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
堆就是一种完全二叉树。
二叉树的储存
逻辑结构和物理结构
逻辑结构和物理结构是计算机科学中两个重要的概念,它们描述了数据在计算机中的不同组织方式。
-
逻辑结构:
- 逻辑结构是指数据元素之间的相互关系和操作规则。它关注的是数据之间的逻辑关联,而不考虑数据在计算机内部的存储方式。
- 常见的逻辑结构包括线性结构、树形结构和图形结构。
- 线性结构中的数据元素之间是一对一的关系,例如线性表、栈、队列等。
- 树形结构中的数据元素之间存在一对多的关系,例如二叉树、B树等。
- 图形结构中的数据元素之间是多对多的关系,例如图、网络等。
-
物理结构:
- 物理结构描述了数据在计算机内部存储的方式和组织形式,也称为存储结构。
- 物理结构与计算机的存储器相关,它包括了数据元素在内存中的存储位置和存储方式。
- 常见的物理结构包括顺序存储结构和链式存储结构。
- 顺序存储结构是将数据元素连续地存储在内存中的一块连续的存储空间中,例如数组。
- 链式存储结构是通过指针将数据元素存储在内存中的不同位置,并通过指针将它们串联起来,例如链表。
逻辑结构关注数据之间的逻辑关系和操作规则,而物理结构关注数据在计算机内部的实际存储方式和组织形式。
二叉树的储存
二叉树有多种存储方式,常见的包括顺序存储和链式存储。
-
顺序存储: 顺序存储通常使用数组来表示二叉树。假设树的根节点存储在数组下标为0的位置,则对于任意一个下标为i的节点:
- 其左子节点的下标为2i + 1
- 其右子节点的下标为2i + 2 例如,如果要存储二叉树的节点值为[1, 2, 3, 4, 5, 6, 7]的完全二叉树,可以使用数组[1, 2, 3, 4, 5, 6, 7]进行存储。
-
链式存储: 链式存储则是通过节点之间的引用来表示二叉树的结构,每个节点包含数据域和左右子节点指针域。
链式储存我们放在后边更新,在这里我们先学习顺序储存。
顺序储存
顺序储存用数组来储存,顺序存储一般只适合用来存储完全二叉树(堆),用顺序储存再存储非完全的二叉树会存在空间浪费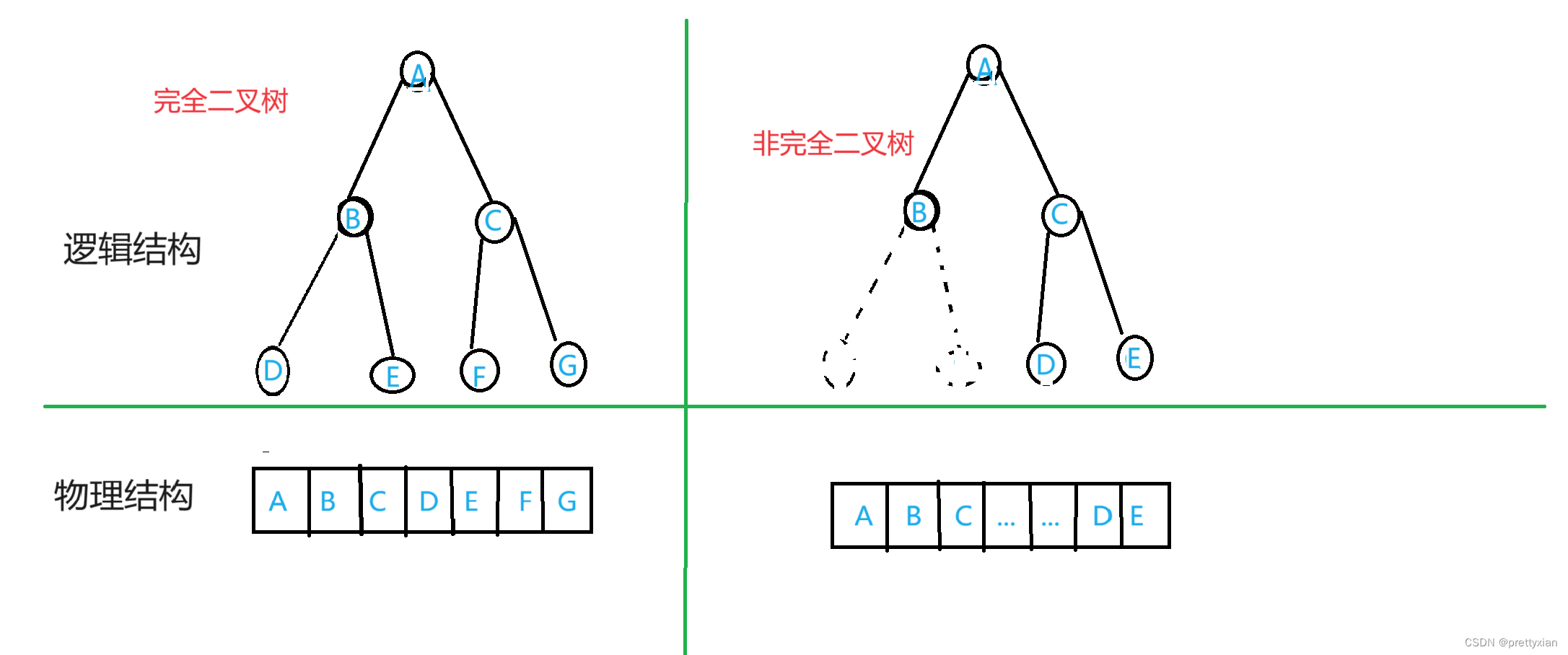
堆的实现
头文件:
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int HPDatatype;typedef struct Heap
{HPDatatype * a;int size;int capacity;}HP;//初始化
void HPInit(HP* php);//插入数据
void HPPush(HP* php, HPDatatype x);//交换
void Swap(HPDatatype* a,HPDatatype * b);//销毁
void HPDestroy(HP* php);//向上调整
void AdjustUp(HPDatatype* a, int child);//向下调整
void AdjustDown(HPDatatype* a,int n, int parent);//删除顶部数据
void HPPop(HP* php);//返回顶部数据
HPDatatype* HPTop(HP* php);//判空
bool HPEmpty(HP* php);实现文件:
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"// 初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;}//插入数据
void HPPush(HP* php, HPDatatype x)
{assert(php);//判断空间够不够if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDatatype* tmp = (HPDatatype* )realloc(php->a,newcapacity * sizeof(HPDatatype));if (tmp == NULL){perror("realloc fail");exit(-1);}php->capacity = newcapacity;php->a = tmp;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//交换
void Swap(HPDatatype* a, HPDatatype* b)
{HPDatatype cmp = *a;*a = *b;*b = cmp;
}//销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}//向上调整
void AdjustUp(HPDatatype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整
void AdjustDown(HPDatatype* a, int n, int parent)
{int child = 2 * parent + 1;//先假设左边的小while (child < n){if (child + 1 < n && a[child + 1] < a[child])//规避chlid + 1 越界的风险{child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}}//删除顶部数据
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--; AdjustDown(php->a, php->size,0);
}//返回顶部数据
HPDatatype* HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}TOP-K问题
一般来说,堆分为两类
-
大堆(Max Heap):在最大堆中,每个节点的值都大于或等于其子节点的值。换句话说,堆顶部的元素是整个堆中的最大值。最大堆常用于实现优先队列,其中具有最高优先级的元素始终位于堆顶。
-
小堆(Min Heap):在最小堆中,每个节点的值都小于或等于其子节点的值。因此,堆顶部的元素是整个堆中的最小值。最小堆也常用于优先队列,其中具有最低优先级的元素位于堆顶。
简单来说大堆中,同一个分支中大的在上;小堆中,同一分支小的在上。
在这里以小堆为例:
向上调整算法
往堆中插入一个数据时,先将插入的数据放到堆的最后一个节点,然后利用向上调整算法依次调整。
图示:
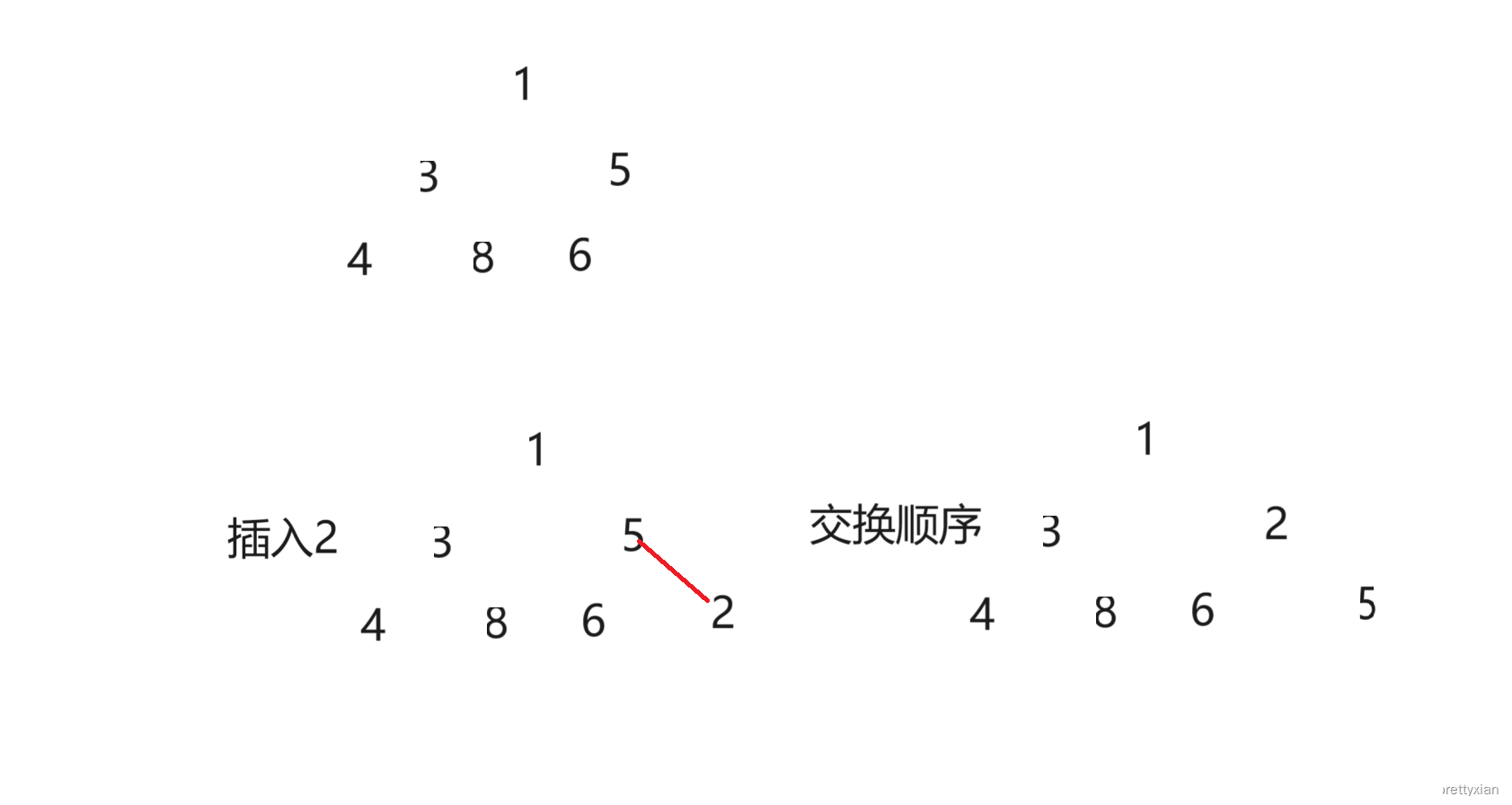
只要子节点不越界循环一直进行,当字节点不小于父节点时跳出if()语句进入else,跳出循环。
//向上调整
void AdjustUp(HPDatatype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
求一堆数据(储存在小堆中)中最最小的前几个数据:将数据插入堆中,小堆的堆顶中储存的就是堆中最小的数据,把堆顶的数据取下来,再将堆顶的数据释放;用向上调整算法调整堆,再依次取堆顶,重复。
//TOP-K
void HPtest02()
{int a[] = { 5,6,1,4,2,8 };HP s;HPInit(&s);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&s, a[i]);}int k = 0;scanf("%d", &k);while (k--){printf("%d ", HPTop(&s));HPPop(&s);}HPDestroy(&s);
}int main()
{HPtest02();return 0;
}演示:
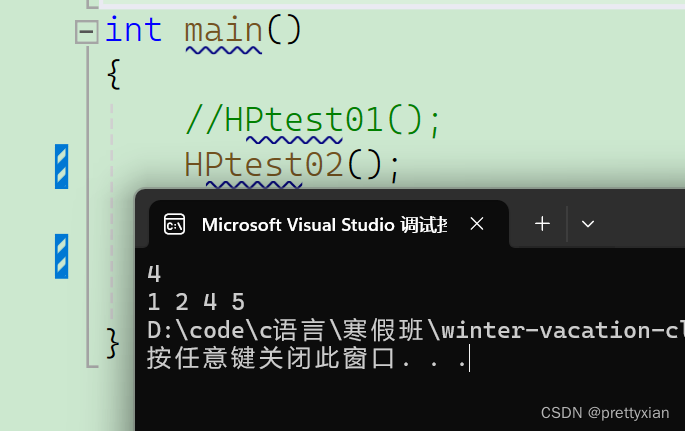
在TOP-K问题中,我们会发现,输出的数据是按顺序拍好的,那么我们可不可以在此基础上进行排序呢。 把数据储存到堆中之后,再依次拿出来。
//排序
void HPtest03()
{int a[] = { 5,6,1,4,2,8 };HP s;HPInit(&s);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&s, a[i]);}int i = 0;while (!HPEmpty(&s)){a[i++] = HPTop(&s);HPPop(&s);}HPDestroy(&s);
}
int main()
{HPtest03();return 0;
}这样我们就可以对数据进行排序。
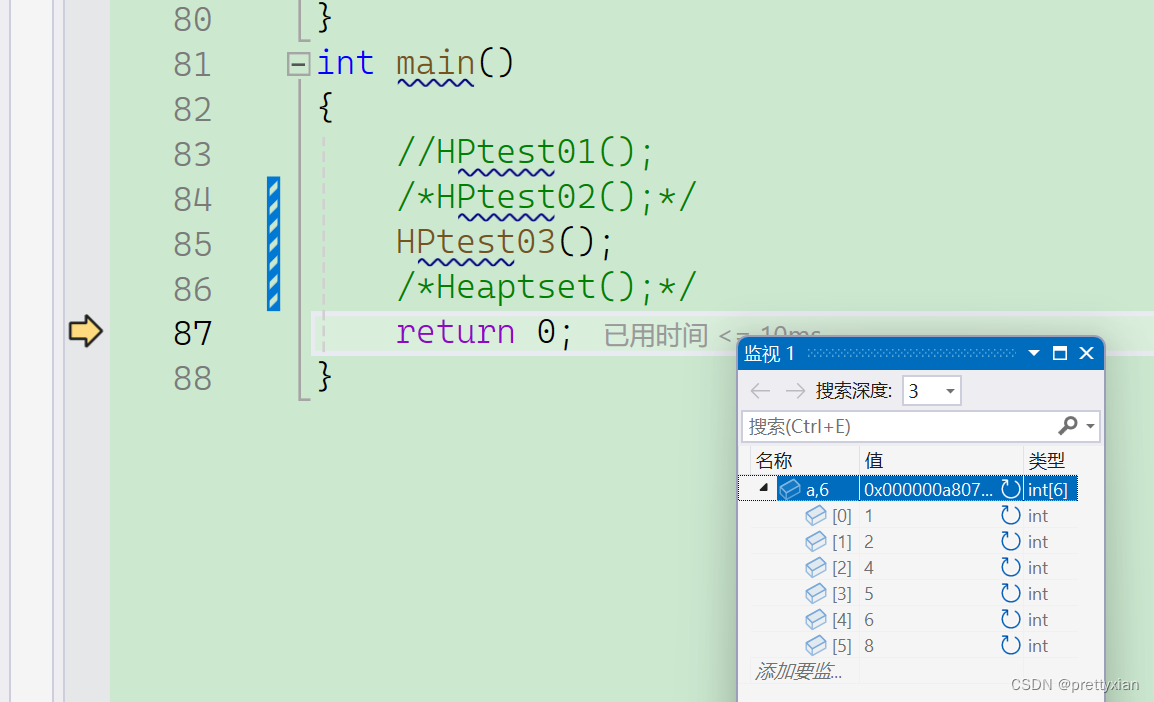
这个算法的时间复杂度非常低 。 一个有k个节点的对的深度为log(k),一条分支最多交换log (k) - 1次,所以
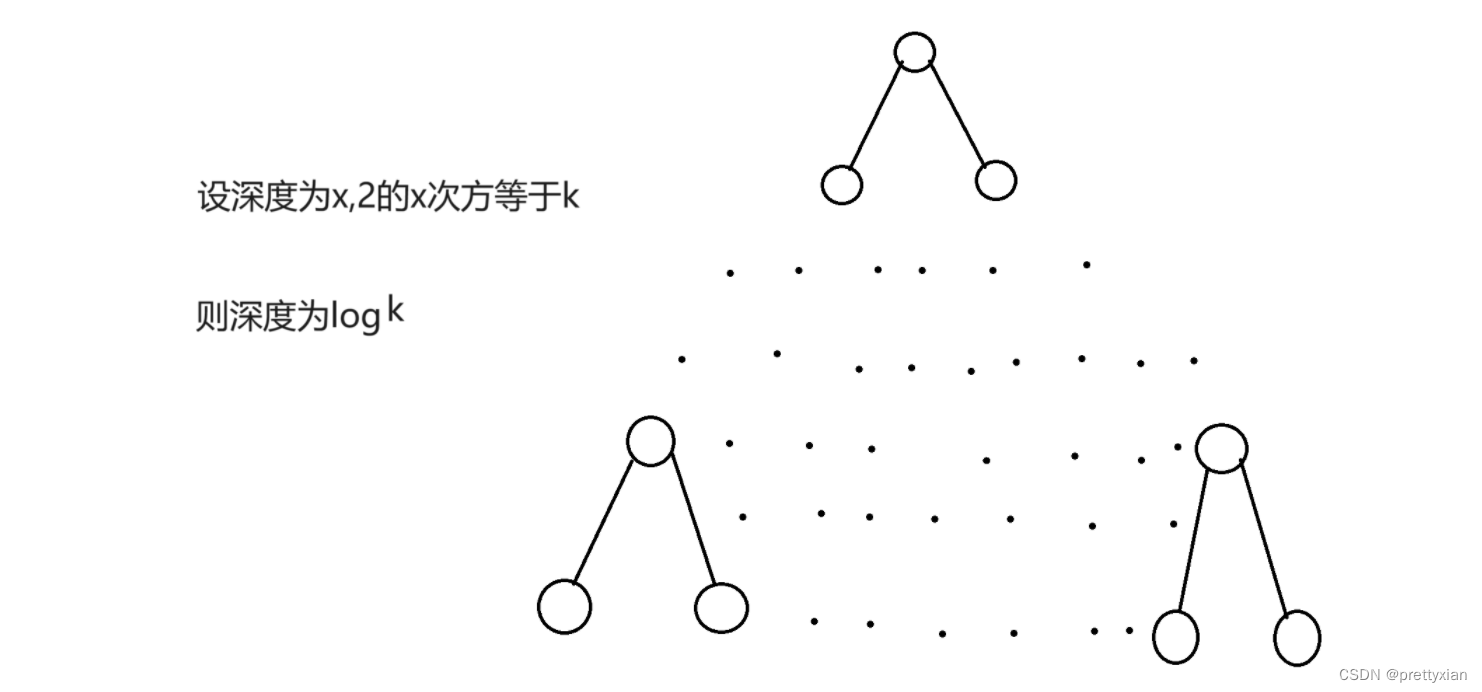
算法的时间复杂度为log N。 但是这并不能称作真正的排序,因为它在原数组的基础上开辟了新的空间。
堆排序
建堆算法
//堆排序
void HeapSort(int* a, int n)
{//建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}
}void Heaptset()
{int a[] = { 5,6,8,4,1,2,3 };HeapSort(a, 7);
}
int main()
{//HPtest01();/*HPtest02();*///HPtest03();Heaptset();return 0;
}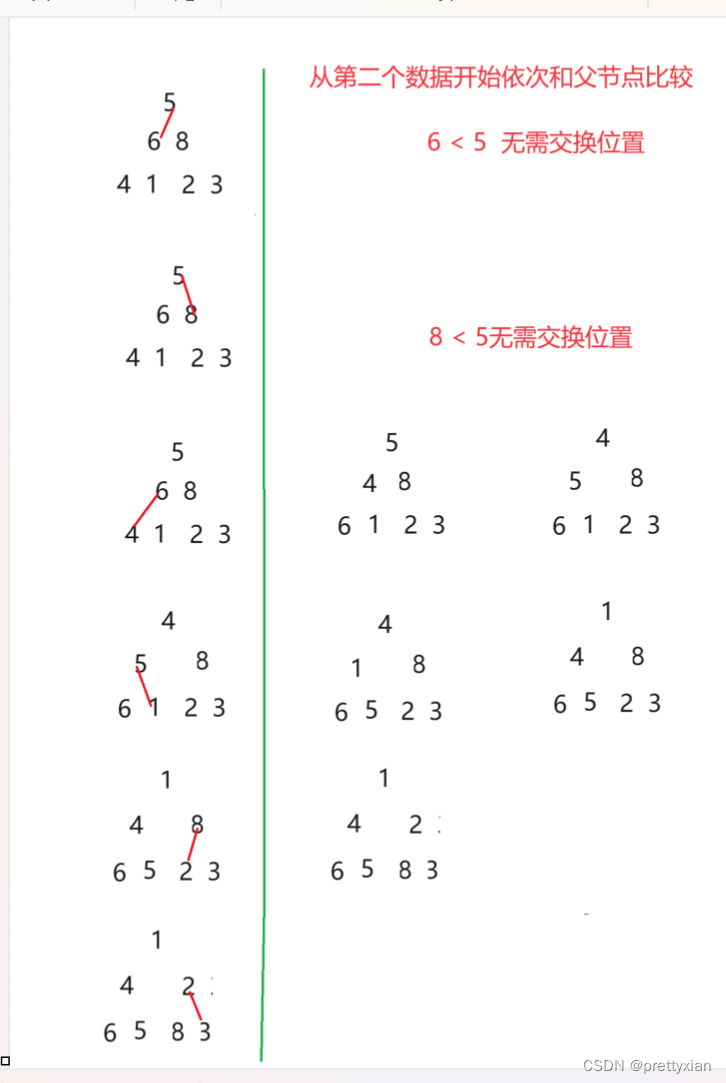
排序
在惯性思维中,要排降序应该会建大堆,排升序会建小堆。但这样会导致一个问题(以建排降序 为建小堆为例)

小堆的堆顶为这组数据中最小的数,我们将它取出,作为排序的第一个数
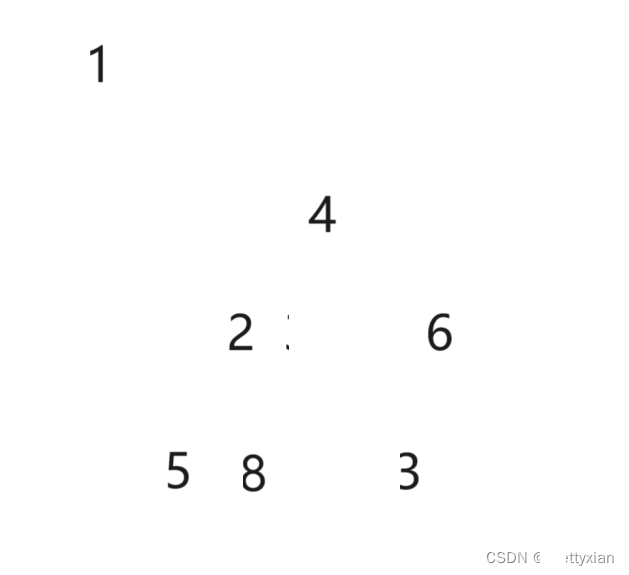
取出堆顶后,找出第二小的数据, 但是此时的堆各个节点已经不满足之前的大小关系了,4之前是6和5的父节点,比6和5大,但是与2为兄弟节点,兄弟节点之间的大小关系原来并不清楚,无法直接找出第二大的数据(可以重新把剩下的数据建堆,但是没必要,时间成本大)。在堆排序中不能让第一个数据直接拿出去,这样会改变节点之间的父子关系,不能确定大小关系,无法找出需要的节点。
接下来以排降序排降序为例演示过程。
//堆排序
void HeapSort(int* a, int n)
{//建堆for (int i = 1; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}void Heaptset()
{int a[] = { 5,6,8,4,1,2,3 };HeapSort(a, 7);
}
int main()
{//HPtest01();/*HPtest02();*///HPtest03();Heaptset();return 0;
}调试:
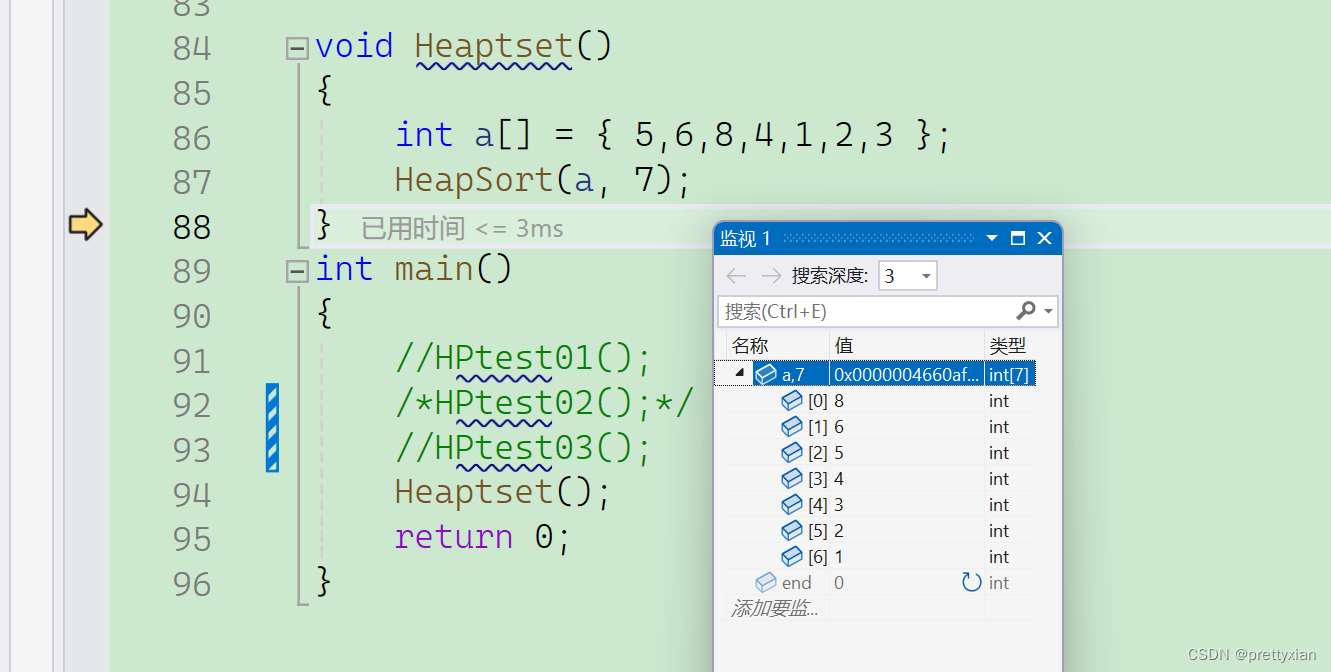
向下调整算法的时间复杂度为log N,堆排序在最坏的情况下N个数据要排N次,所以堆排序的时间复杂度为N log N。可以极大的提高程序的效率。
相关文章:

【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入 要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点: 根节点(Root):树的顶部节…...

C#面:XML与 HTML 的主要区别是什么
C# XML与HTML有以下几个主要区别: 用途不同:XML(eXtensible Markup Language)是一种用于存储和传输数据的标记语言,它的主要目的是描述数据的结构和内容。HTML(HyperText Markup Language)是一…...

java并发-如何保证线程按照顺序执行?
【readme】 使用只有单个线程的线程池(最简单)Thread.join() 可重入锁 ReentrantLock Condition 条件变量(多个) ; 原理如下: 任务1执行前在锁1上阻塞;执行完成后在锁2上唤醒;任务…...

PyCharm中 Fitten Code插件的使用说明一
一. 简介 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省您的时间,另外还可以对话聊天,解决您编程碰到的问题。 前一篇文章学习了 PyCharm…...
Polar Web【简单】PHP反序列化初试
Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境,显示下图中的PHP代码,于是展开分析: 首先发现Easy类中有魔术函数 __wakeup() ,实现的是对成员…...
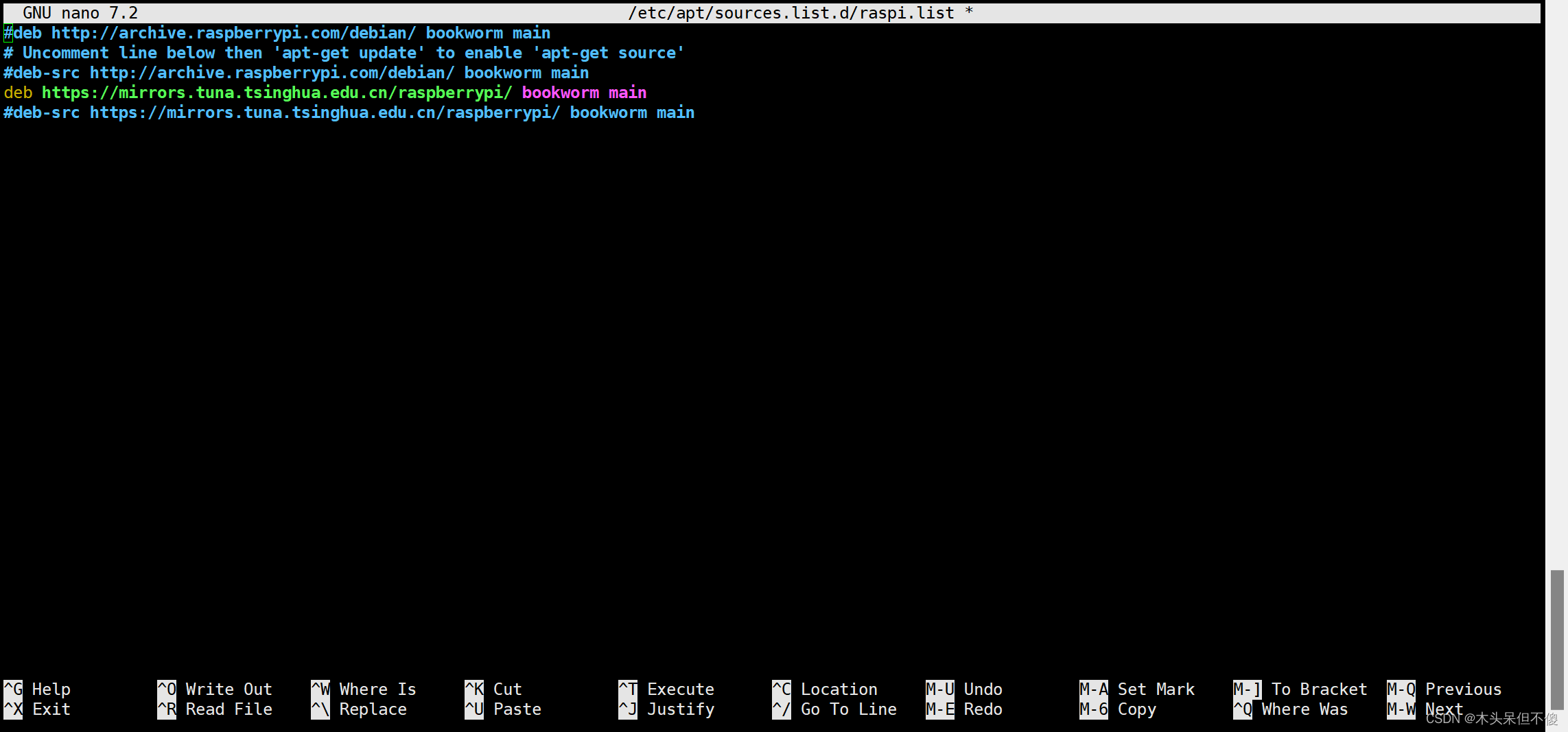
树莓派4B 零起点(二) 树莓派 更换软件源和软件仓库
目录 一、准备工作,查看自己的树莓派版本 二、安装HTTPS支持 三、更换为清华源 1、更换Debian软件源 2,更换Raspberrypi软件仓库 四、进行软件更新 接前章,我们的树莓派已经启动起来了,接下来要干的事那就是更换软件源和软件…...
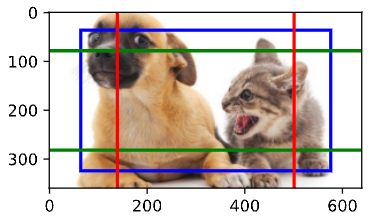
Pytorch 实现目标检测二(Pytorch 24)
一 实例操作目标检测 下面通过一个具体的例子来说明锚框标签。我们已经为加载图像中的狗和猫定义了真实边界框,其中第一个 元素是类别(0代表狗,1代表猫),其余四个元素是左上角和右下角的(x, y)轴坐标(范围…...
进行高效列表操作)
如何使用Python中的列表解析(list comprehension)进行高效列表操作
Python中的列表解析(list comprehension)是一种创建列表的简洁方法,它可以在单行代码中执行复杂的循环和条件逻辑。列表解析提供了一种快速且易于阅读的方式来生成新的列表。 以下是一些使用列表解析进行高效列表操作的示例: 1.…...

java使用websocket遇到的问题
java使用websocket的bug 1 websocket连接正常但是收不到服务端发出的消息java的websocket并发的时候导致连接断开(看着连接是正常的,但是实际上已经断开) 1 websocket连接正常但是收不到服务端发出的消息 java的websocket并发的时候导致连接断…...

[Cloud Networking] Layer 2
文章目录 1. 什么是Mac Address?2. 如何查找MAC地址?3. 二层数据交换4. [Layer 2 Protocol](https://blog.csdn.net/settingsun1225/article/details/139552315) 1. 什么是Mac Address? MAC 地址是计算机的唯一48位硬件编码,嵌入到网卡中。 MAC地址也…...
)
[240609] qwen2 发布,在 Ollama 已可用 | 采用语言模型构建通用 AGI(2020年8月)
目录 qwen2 发布,在 Ollama 已可用Qwen2 模型概览 (基于 Ollama 网站信息)一、模型介绍二、模型参数三、支持语言 (除英语和中文外)四、模型性能五、许可证六、数据支撑: 采用语言模型构建通用 AGI qwen2 发布,在 Ollama 已可用 Qwen2 模型概览 (基于 O…...
)
赶紧收藏!2024 年最常见 20道分布式、微服务面试题(五)
上一篇地址:赶紧收藏!2024 年最常见 20道分布式、微服务面试题(四)-CSDN博客 九、在分布式系统中,如何保证数据一致性? 在分布式系统中保证数据一致性是一个复杂的问题,因为分布式系统由多个独…...

为什么Kubernetes(K8S)弃用Docker:深度解析与未来展望
为什么Kubernetes弃用Docker:深度解析与未来展望 🚀 为什么Kubernetes弃用Docker:深度解析与未来展望摘要引言正文内容(详细介绍)什么是 Kubernetes?什么是 Docker?Kubernetes 和 Docker 的关系…...
软件游戏提示msvcp120.dll丢失的解决方法,总结多种靠谱的解决方法
在电脑使用过程中,我们可能会遇到一些错误提示,其中之一就是“找不到msvcp120.dll”。那么,msvcp120.dll是什么?它对电脑有什么影响?有哪些解决方法?本文将从以下几个方面进行探讨。 一,了解msv…...
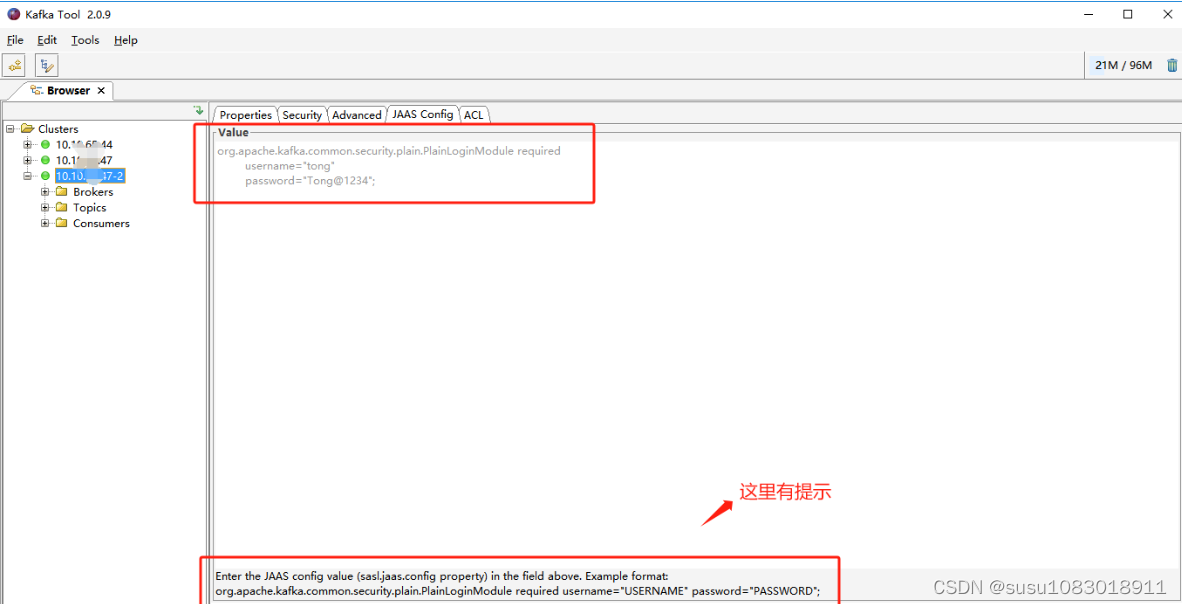
使用kafka tools工具连接带有用户名密码的kafka
使用kafka tools工具连接带有用户名密码的kafka 创建kafka连接,配置zookeeper 在Security选择Type类型为SASL Plaintext 在Advanced页面添加如下图红框框住的内容 在JAAS_Config加上如下配置 需要加的配置: org.apache.kafka.common.security.plain.Pla…...

[个人感悟] Java基础问题应该考察哪些问题?
前言 “一切代码无非是数据结构和算法流程的结合体.” 忘了最初是在何处看见这句话了, 这句话, 对于Java基础的考察也是一样. 正如这句话所说, 我们对于基础的考察主要考察, 数据结构, 集合类型结构, 异常类型, 已经代码的调用和语法关键字. 其中数据结构和集合类型结构是重点…...
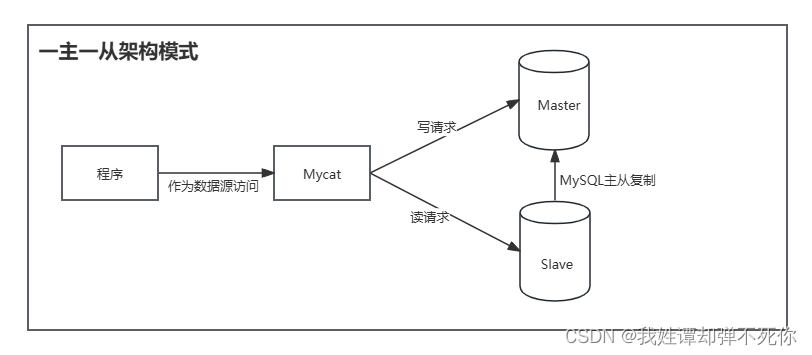
MySQL-主从复制
1、主从复制的理解 在工作用常见Redis作为缓存与MySQL一起使用。当有请求时,首先会从缓存中进行查找,如果存在就直接取出,否则访问数据库,这样 提升了读取的效率,也减少了对后台数据库的访问压力。Redis的缓存架构时高…...

开发没有尽头,尽力既是完美
最近遇到了一些难题,开发系统总有一些地方没有考虑周全,偏偏用户使用的时候“完美复现”了这个隐藏的Bug...... 讲道理创业一年之久为了生存,我一直都有在做复盘,复盘的核心就是:如何提升营收、把控开发质量࿰…...

【手推公式】如何求SDE的解(附录B)
【手推公式】如何求SDE的解(附录B) 核心思路:不直接求VE和VP的SDE的解xt,而是求xt的期望和方差,从而写出x0到xt的条件分布形式(附录B) 论文:Score-Based Generative Modeling throug…...
STM32F103单片机工程移植到航顺单片机HK32F103注意事项
一、简介 作为国内MCU厂商中前三阵营之一的航顺芯片,建立了世界首创超低功耗7nA物联网、万物互联核心处理器浩瀚天际10X系列平台,接受代理商/设计企业/方案商定制低于自主研发十倍以上成本,接近零风险自主品牌产品,芯片设计完成只…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
