DP:回文串模型
一、回文子串
. - 力扣(LeetCode)

该题有3种解法
(1)中心扩展算法(在字符串章节有介绍)时间复杂度O(N^2),空间复杂度O(1)
(2)马丁车算法(专门用来解决回文串问题,但是适用返回太窄)时间复杂度O(N),空间复杂度O(N)
(3)动态规划(可以将所有回文信息都保存在dp表中)时间复杂度O(N^2),空间复杂度O(N^2)
这边重点介绍动态规划的做法。
算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示s字符串[i,j]的子串是否是回文串(i<=j)只需处理右上区即可
2、状态转移方程
dp[i][j]:
(1)s[i]!=s[j]——>false
(2)s[i]==s[j]——>
i==j true
i+1==j true
dp[i+1][j-1]
3、初始化
无需初始化
4、填表顺序
dp[i][j]会用到dp[i+1][j-1],所以必须要从下往上填 , 左右顺序不重要
5、返回值
dp表中true的个数
class Solution {
public:int countSubstrings(string s) {//动态规划的做法int ret=0;//s[i]==s[j] 1、i==j 2、i+1==j 3、dp[i+1][j-1]?int n=s.size();vector<vector<bool>> dp(n,vector<bool>(n));//只要右上半区 for(int i=n-1;i>=0;--i) //要从下往上 左右无所谓,因为用不到for(int j=i;j<n;++j) //只要右上半区if(s[i]==s[j]) ret+=dp[i][j]=i+1<j?dp[i+1][j-1]:true;return ret;}
};二、最长回文子串
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示s字符串[i,j]的子串是否是回文串(i<=j)只需处理右上区即可
2、状态转移方程
dp[i][j]:
(1)s[i]!=s[j]——>false
(2)s[i]==s[j]——>
i==j true
i+1==j true
dp[i+1][j-1]
3、初始化
无需初始化
4、填表顺序
dp[i][j]会用到dp[i+1][j-1],所以必须要从下往上填 , 左右顺序不重要
5、返回值
dp表中为true以及长度最大的子串的起始位置和长度
class Solution {
public:string longestPalindrome(string s) {//动态规划的思想int begin=0,len=1;//帮助我们返回结果int n=s.size();vector<vector<bool>> dp(n,vector<bool>(n));for(int i=n-1;i>=0;--i)for(int j=i;j<n;++j) //右上角部分{if(s[i]==s[j]) {dp[i][j]=i+1<j?dp[i+1][j-1]:true;if(dp[i][j]&&len<j-i+1) {begin=i;len=j-i+1;}} }return s.substr(begin,len);}
};三、分割回文子串I
. - 力扣(LeetCode)

解法1:动归预处理+回溯
class Solution {
public://动归预处理+回溯vector<vector<bool>> dp;//dp预处理vector<vector<string>> ret;//记录返回的结果vector<string> path;//记录路径的结果int n;vector<vector<string>> partition(string s) {//dp预处理n=s.size();dp.resize(n,vector<bool>(n));for(int i=n-1;i>=0;--i)for(int j=i;j<n;++j)if(s[i]==s[j]) dp[i][j]=i+1<j?dp[i+1][j-1]:true;//将dp数组交给dfs去处理dfs(s,0);return ret;}void dfs(string&s,int i){if(i==n) {ret.push_back(path);return;}for(int j=i;j<n;++j)if(dp[i][j]){path.emplace_back(s.substr(i,j-i+1));dfs(s,j+1);path.pop_back();}}
};解法2:回溯+记忆化搜索
class Solution {
public:
//回溯+记忆化搜索vector<vector<int>> f;//记忆化数组 0表示未搜索,1表示回文,-1表示不回文vector<vector<string>> ret;//记录返回的结果vector<string> path;//记录路径的结果int n;vector<vector<string>> partition(string s) {n=s.size();f.resize(n,vector<int>(n));//交给dfs帮助我们解决dfs(s,0);return ret;}void dfs(const string&s,int i){if(i==n) {ret.emplace_back(path);return;}for(int j=i;j<n;++j)if(ispal(s,i,j)){path.emplace_back(s.substr(i,j-i+1));dfs(s,j+1);path.pop_back();}}bool ispal(const string&s,int i,int j) //判断i->j是否回文{//先看看备忘录if(f[i][j]) return f[i][j];if(s[i]!=s[j]) return f[i][j]=false;else return f[i][j]=i+1<j?ispal(s,i+1,j-1):true;}
};四、分割回文子串II
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i]表示s字符串[0,i]区间上的最长子串的最小分割次数
2、状态转移方程
dp[i]:
(1)0-i回文——>0
(2)0-i不是回文——>j-i是否回文——>min(dp[i],dp[j-1]+1)
3、初始化
都初始化为整型最大值,否则最后dp表里都是0会影响结果
4、填表顺序
dp[i][j]会用到dp[i+1][j-1],所以必须要从下往上填 , 左右顺序不重要
5、返回值
dp[n-1]
class Solution {
public:int minCut(string s) {int n=s.size();vector<vector<bool>> ispal(n,vector<bool>(n));for(int i=n-1;i>=0;--i)for(int j=i;j<n;++j) //右上角部分if(s[i]==s[j]) ispal[i][j]=i+1<j?ispal[i+1][j-1]:true;//第二次枚举 尝试去分割 vector<int> dp(n,INT_MAX);//初始化为无穷大 for(int i=0;i<n;++i)//先看看左边的部分if(ispal[0][i]) dp[i]=0;elsefor(int j=1;j<=i;++j)//去看看左边 要怎么切割 左开右闭if(ispal[j][i]) dp[i]=min(dp[i],dp[j-1]+1);//j代表最后一个回文串的起始位置return dp[n-1];}
};五、分割回文子串III(经典)
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示对于字符串的前i个字符,将他分割成j个子串,所需修改的最少字符数
2、状态转移方程
int cost(string&s,int l,int r) 表示从s的i-j位置,变成回文串所需要的最小修改次数
dp[i][j]:
(1)j==1(没有分割) cost(s,0,i-1)
(2)j>1——>min(dp[i][j],dp[m][j-1]+cost(s,m,i-1))
3、初始化
初始化成INT_MAX 确保不影响最终结果 dp[0][0]=0 确保不影响结果
4、填表顺序
上到下,左到右
5、返回值
dp[n][k]
class Solution {
public:int palindromePartition(string s, int k) {//dp[i][j]表示对于字符串的前i个字符,将他分割成j个子串,所需修改的最少字符数int n=s.size();vector<vector<int>> dp(n+1,vector<int>(k+1,INT_MAX));dp[0][0]=0;for(int i=1;i<=n;++i)for(int j=1;j<=min(k,i);++j)if(j==1) dp[i][j]=cost(s,0,i-1);else for(int m=j-1;m<i;++m) dp[i][j]=min(dp[i][j],dp[m][j-1]+cost(s,m,i-1));//找前面的状态 0->i 分成j个//dp0->m+ cost m->ireturn dp[n][k];//0->n k}int cost(string&s,int l,int r){int ret=0;for(int i=l,j=r;i<j;++i,--j)if(s[i]!=s[j]) ++ret;//需要修改一个才能成为回文return ret;}
};六、分割回文串IV
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示s字符串[i,j]的子串是否是回文串(i<=j)只需处理右上区即可
2、状态转移方程
dp[i][j]:
(1)s[i]!=s[j]——>false
(2)s[i]==s[j]——>
i==j true
i+1==j true
dp[i+1][j-1]
3、初始化
无需初始化
4、填表顺序
dp[i][j]会用到dp[i+1][j-1],所以必须要从下往上填 , 左右顺序不重要
5、返回值
第二次枚举,先固定第一个位置,然后固定第二个位置,看看由两个位置分割出来的三个区域是否都为true
class Solution {
public:bool checkPartitioning(string s) {//将结果存到dp表中int n=s.size();vector<vector<bool>> dp(n,vector<bool>(n));for(int i=n-1;i>=0;--i)for(int j=i;j<n;++j) //右上角部分if(s[i]==s[j]) dp[i][j]=i+1<j?dp[i+1][j-1]:true;//第二次枚举 先固定第一个,然后固定第二个,然后看看3个是不是都是true即可for(int i=1;i<n-1;++i)for(int j=i;j<n-1;++j)if(dp[0][i-1]&&dp[i][j]&&dp[j+1][n-1]) return true;return false;}
};七、不重叠回文子字符串的最大数目
. - 力扣(LeetCode)


class Solution {
public:int maxPalindromes(string s, int k) {//dp[i]表示0->i中的不重叠回文子字符串的最大数目int n=s.size();vector<int> dp(n+1);//如果s[i]不在回文串中 dp[i+1]=dp[i]//如果s[r]在回文串中,采用中心扩展,l->r是回文子串,且r-l+1>=k 有dp[i]=max(dp[i],dp[l-1]+1)for(int i=0;i<n*2-1;++i){//两边到中间不适合判断长度,应该从中间到两边int l=i/2,r=l+i%2; //中心扩展判断是否回文dp[l+1]=max(dp[l],dp[l+1]);for(;l>=0&&r<n&&s[l]==s[r];--l,++r)if(r-l+1>=k){dp[r+1]=max(dp[r+1],dp[l]+1);break;}}return dp[n];}
};八、最长回文子序列
. - 力扣(LeetCode)

class Solution {
public:int longestPalindromeSubseq(string s) {//子序列和子串的区别就是可以不连续int n=s.size();vector<vector<int>> dp(n,vector<int>(n));//只会用到右上半部分for(int i=n-1;i>=0;--i){//dp[i][j]表示i-j区间内所有子序列中,最长回文子序列的长度dp[i][i]=1;for(int j=i+1;j<n;++j)if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2; //i+1=j的情况可以不用考虑 //虽然会出现用不到的格子,但是里面是0所以不会影响计算结果else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);}return dp[0][n-1];}
};算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示s字符串[i,j]所有子序列中的最长子序列的长度
2、状态转移方程
dp[i][j]:
(1)s[i]!=s[j]——>max(dp[i,j-1],dp[i+1][j])
(2)s[i]==s[j]——>
i==j 1
i+1==j 2
dp[i+1][j-1]+2
3、初始化
初始化为0 dp[i][i]=1
4、填表顺序
上到下,左到右
5、返回值
dp[0][n-1]
九、让字符串成为回文串的最小插入次数
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示s字符串[i,j]子串,使他成为回文子串的最小插入次数
2、状态转移方程
dp[i][j]:
(1)s[i]!=s[j]——>min(dp[i,j-1],dp[i+1][j])+1
(2)s[i]==s[j]——>
i==j 0
i+1==j 0
dp[i+1][j-1]
3、初始化
初始化为0
4、填表顺序
下往上,左到右
5、返回值
dp[0][n-1]
class Solution {
public:int minInsertions(string s) {int n=s.size();vector<vector<int>> dp(n,vector<int>(n));for(int i=n-1;i>=0;--i)for(int j=i+1;j<n;++j)if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1];else dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;return dp[0][n-1];}
}; 
相关文章:

DP:回文串模型
一、回文子串 . - 力扣(LeetCode) 该题有3种解法 (1)中心扩展算法(在字符串章节有介绍)时间复杂度O(N^2),空间复杂度O(1) (2)马丁车…...

STM32CubeMX软件的安装以及配置
STM32CubeMX软件的配置过程可以详细分为以下几个步骤,以确保您能够顺利地使用该软件进行STM32微控制器的配置和代码生成: 1. 安装前准备 安装JAVA环境:由于STM32CubeMX软件是基于JAVA环境运行的,所以需要先安装Java Runtime Env…...

【适配鸿蒙next】Flutter 新一代混合栈管理框架
前言 据最新消息显示,华为今年下半年将全面转向其自主平台HarmonyOS,放弃Android系统。 报道中提到,下一版HarmonyOS预计将随华为即将推出的Mate 70旗舰系列一起发布。 据悉,HarmonyOS Next 已经扩展到4000个应用程序,…...

车载电子电气架构 --- 车载信息安全
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...
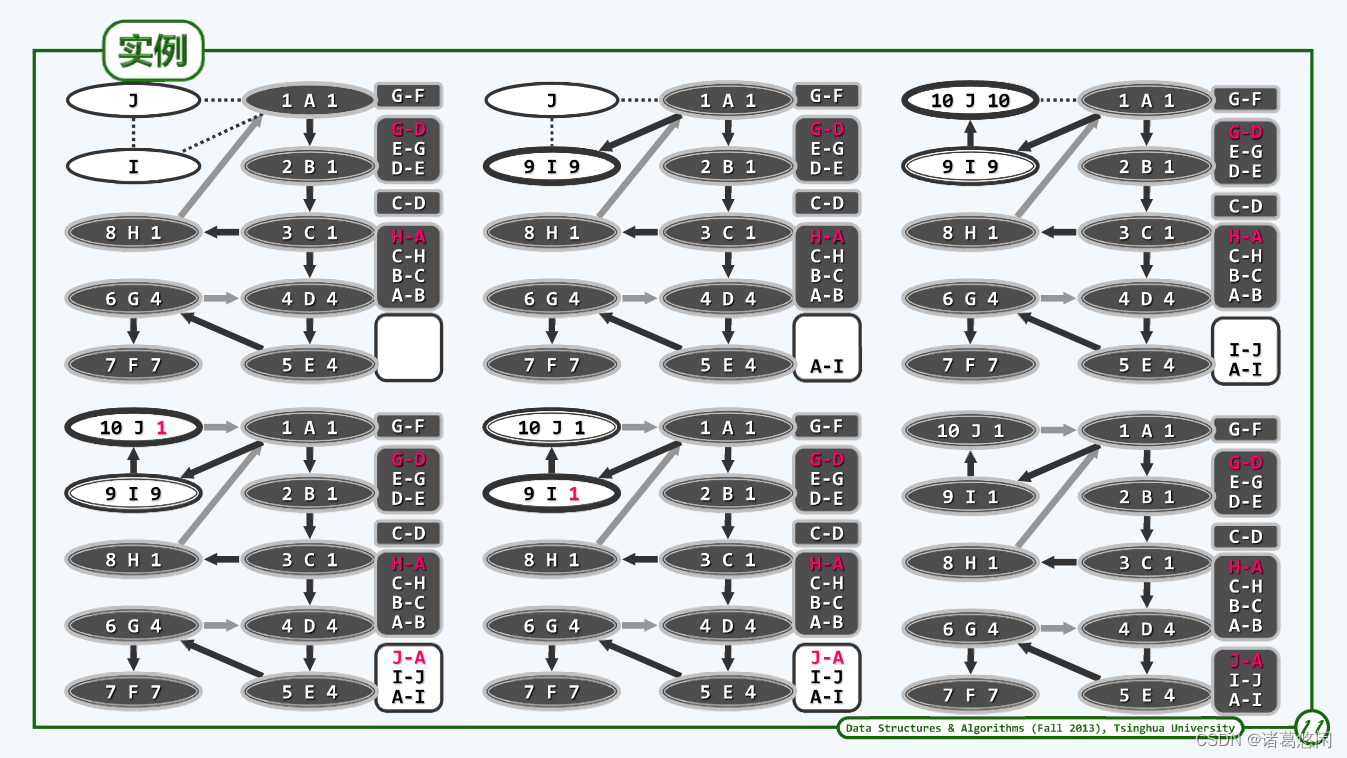
【数据结构(邓俊辉)学习笔记】图04——双连通域分解
文章目录 0. 概述1 关节点与双连通域2 蛮力算法3 可行算法4 实现5 示例6 复杂度 0. 概述 学习下双连通域分解,这里略微有一点点难,这个算是DFS算法的非常非常经典的应用,解决的问题也非常非常有用。 1 关节点与双连通域 连通性很好理解&am…...

UI学习(二)
UI学习(二) 文章目录 UI学习(二)布局子视图手动布局自动布局 导航控制器导航控制器基础导航控制器的切换导航栏工具栏 分栏控制器分栏控制器协议部分的内容UITableView基础部分相关的协议函数高级协议与单元格 多界面传值 布局子视…...

【嵌入式】波特率9600,发送8个字节需要多少时间,如何计算?
问题: 波特率9600,发送 01 03 00 00 00 04 44 09 (8字节) 需要多少时间,如何计算? 在计算发送数据的时间时,首先要考虑波特率以及每个字符的数据格式。对于波特率9600和标准的UART数据格式(1个起始位&…...
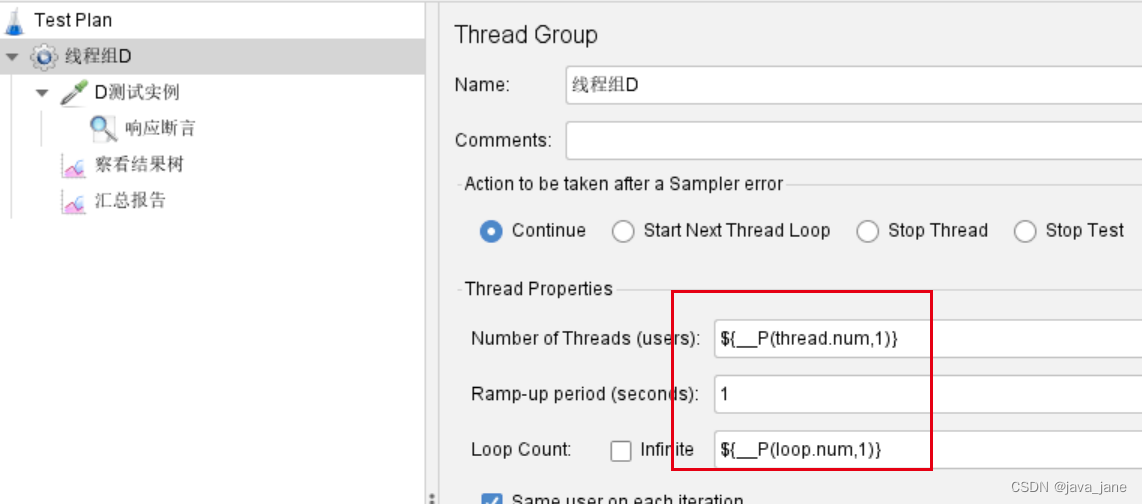
jmeter -n -t 使用非GUI模式运行脚本说明
命令模式下执行jmx文件 jmeter -n -t fatie.jmx -l results\t4.jtl -e -o results\h1 表示以命令行模式运行当前目录下的脚本fatie.jmx,将结果存入当前目录下的results\t1.jtl,并且生成html格式的报告,写入文件夹results\h1。 说明:生成结果的文件夹r…...

网络流媒体协议——HLS协议
HTTP 实时流媒体(HTTP Live Streaming,HLS)协议是苹果公司提出的主要用于直播的流媒体协议。一个完整的基于HLS协议的流媒体直播系统由四部分组成,即音视频采集器、媒体服务器、媒体分发器和播放客户端。 媒体服务器 媒体服务器的…...
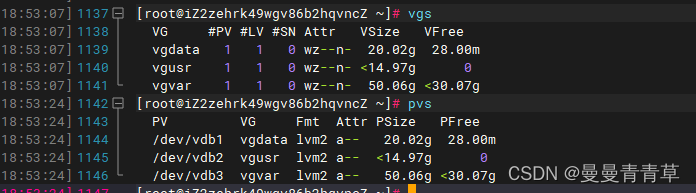
Linux服务器扩容及磁盘分区(LVM和非LVM)
Linux扩容及磁盘分区(LVM和非LVM) 本文主要介绍了阿里云服务器centos的扩容方法:非LVM分区扩容方法(系统盘),以及磁盘改LVM并分区(数据盘)。主要是ext4文件系统及xfs磁盘scsi MBR分…...

支持向量机
支持向量机(SVM) 支持向量机(Support Vector Machine, SVM)是一种用于分类和回归任务的监督学习算法。SVM 的核心思想是找到一个最优的决策边界(或称为超平面),以最大化不同类别之间的间隔。以…...

Kafka 架构
1 整体架构 1.1 Zookeeper Zookeeper 是一个分布式协调服务,用于管理 Kafka 的元数据。它负责维护 Kafka 集群的配置信息、Broker 列表和分区的 Leader 信息。 Zookeeper 确保了 Kafka 集群的高可用性和可靠性。 但 Zookeeper 已经成为 Kafka 性能瓶颈,…...

iOS 查看runtime源码的几种方法
目录 前言 查看runtime 源码方法 1.下载 Apple 官方提供的源代码 2.通过 GitHub 访问镜像 3.使用命令行工具查看 4.示例 前言 这篇博客主要介绍了查看iOS runtime源代码的方法。 查看runtime 源码方法 查看iOS runtime源码的方法包括以下几个步骤: 1.下载 A…...
底板外设倒灌到处理器分析
在嵌入式系统中,底板外设通常与处理器通过各种接口(如UART、SPI、I2C、GPIO等)进行连接。这些外设可能包括传感器、执行器、存储器、通信模块等。倒灌是指当外设向处理器提供的信号电平超出了处理器能够接受的范围,导致处理器无法…...
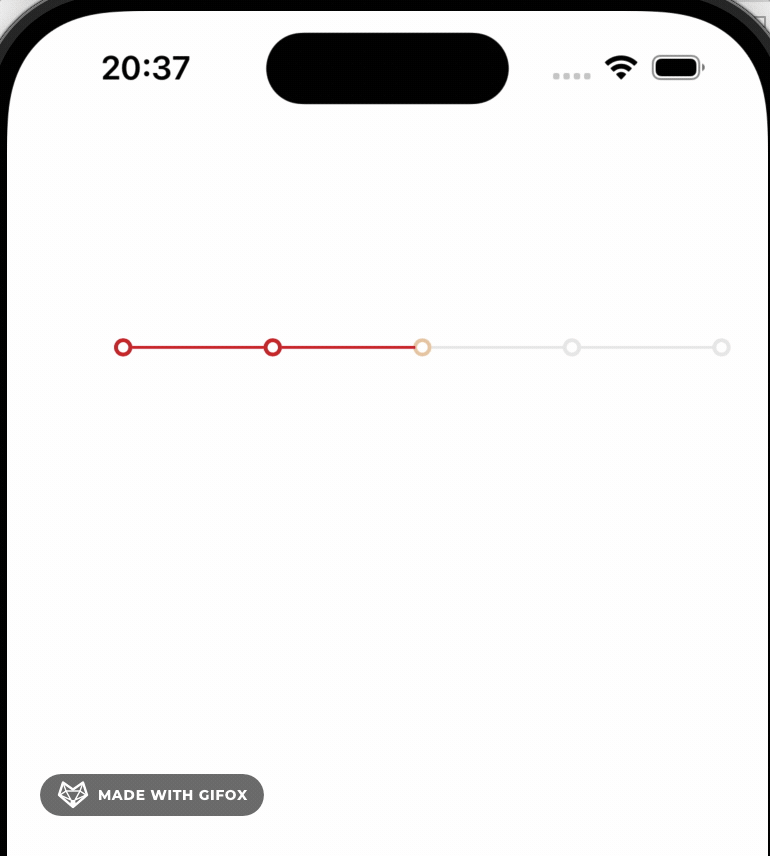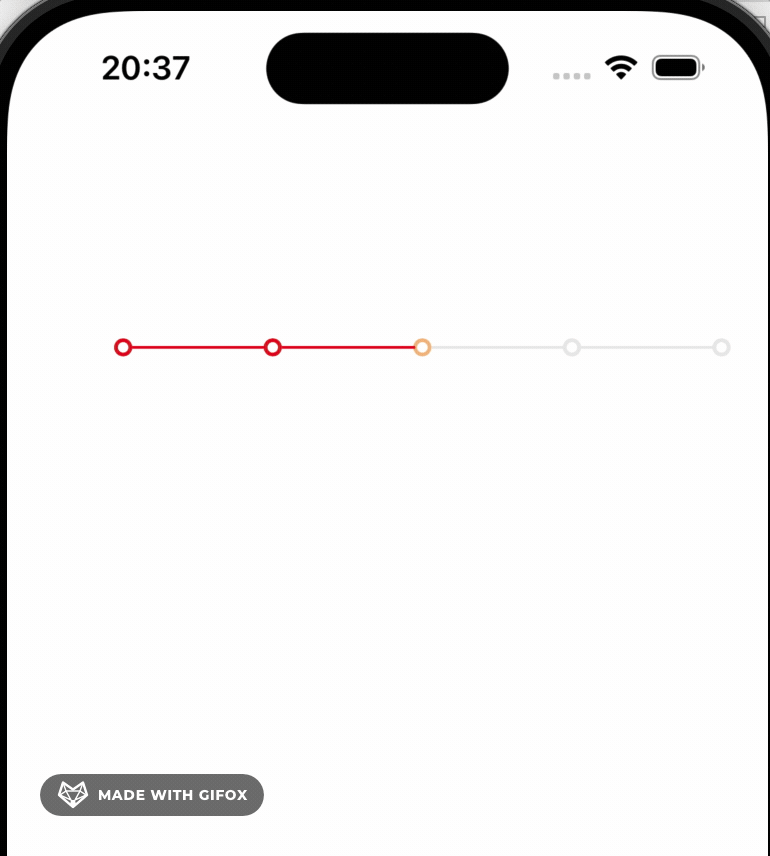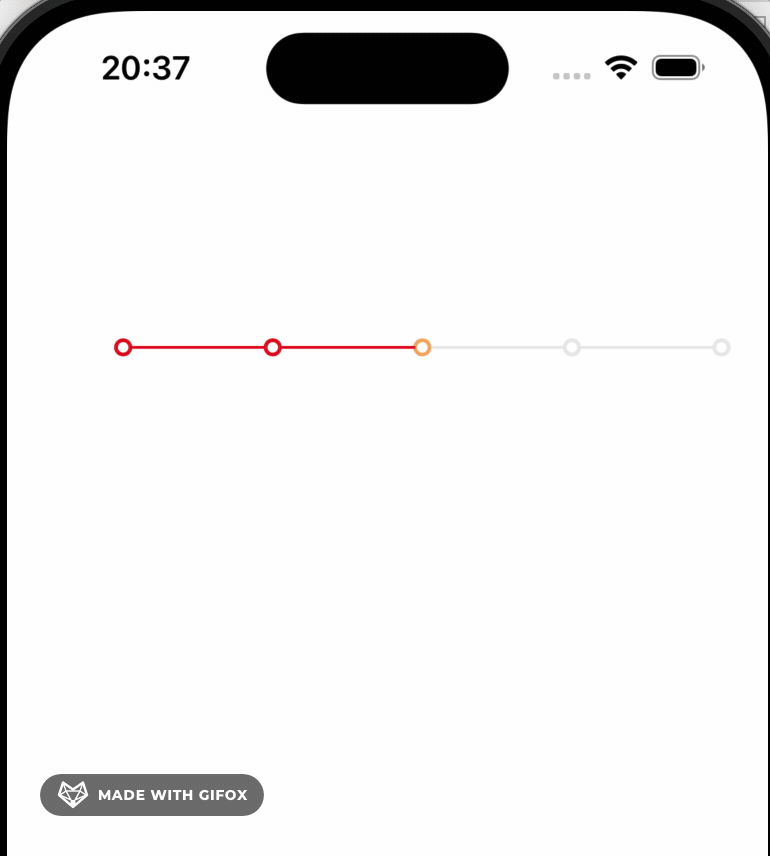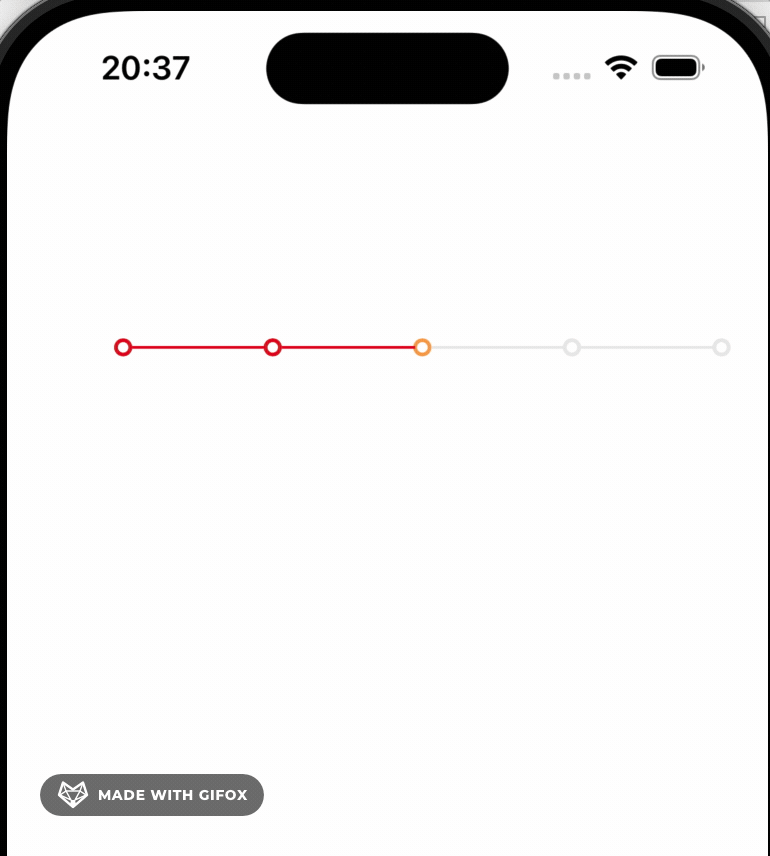
使用贝塞尔曲线实现一个iOS时间轴
UI效果 实现的思路 就是通过贝塞尔曲线画出时间轴的圆环的路径,然后 使用CAShaper来渲染UI,再通过 animation.beginTime [cilrclLayer convertTime:CACurrentMediaTime() fromLayer:nil] circleTimeOffset 来设置每个圆环的动画开始时间, …...
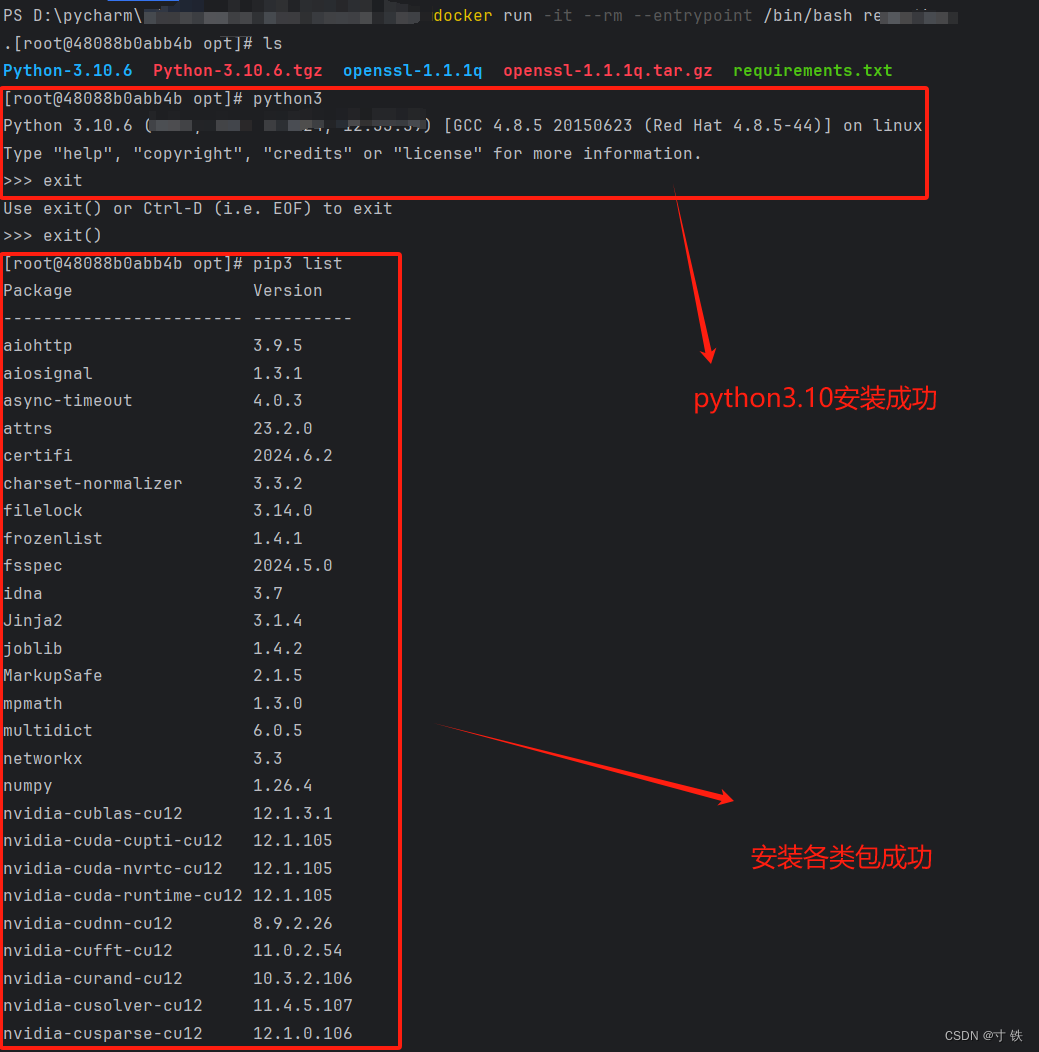
【深度学习】深度学习之巅:在 CentOS 7 上打造完美Python 3.10 与 PyTorch 2.3.0 环境
【深度学习】深度学习之巅:在 CentOS 7 上打造完美Python 3.10 与 PyTorch 2.3.0 环境 大家好 我是寸铁👊 总结了一篇【深度学习】深度学习之巅:在 CentOS 7 上打造完美Python 3.10 与 PyTorch 2.3.0 环境✨ 喜欢的小伙伴可以点点关注 &#…...

在docker容器中使用gdb调试python3.11的进程
gdb调试python进程的前提条件 安装python及python调试信息安装gdb工具安装python-gdb.py扩展 安装过程 我们使用docker来安装以上内容,Dockerfile文件内容如下: FROM docker.io/centos:7.4.1708# 安装依赖 RUN yum install -y -q epel-release &…...

堆排序要点和难点以及具体案例应用
堆排序(Heap Sort)是一种基于堆数据结构的排序算法。下面我将以分点表示和归纳的方式,结合相关数字和信息,详细描述堆排序的PTA(Programming and Testing Approach,编程与测试方法)。 1. 堆排序原理 堆排序是一种树形选择排序,利用了完全二叉树的性质,通过构建最大堆…...
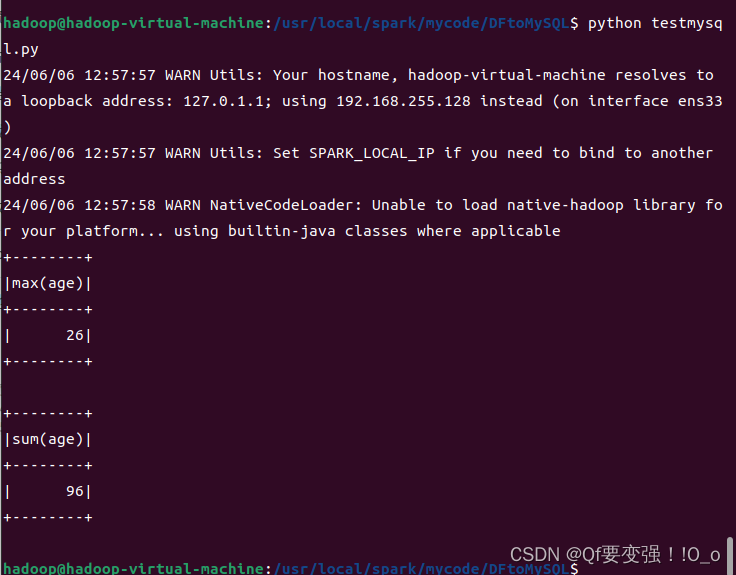
pyspark中使用mysql jdbc报错java.lang.ClassNotFoundException: com.mysql.jdbc.Driver解决
报错信息: py4j.protocol.Py4JJavaError: An error occurred while calling o33.load. : java.lang.ClassNotFoundException: com.mysql.jdbc.Driver 我的解决方法: 这个报错就是提示你找不到jar包,所以你需要去下载一个和你mysql版本匹配的j…...
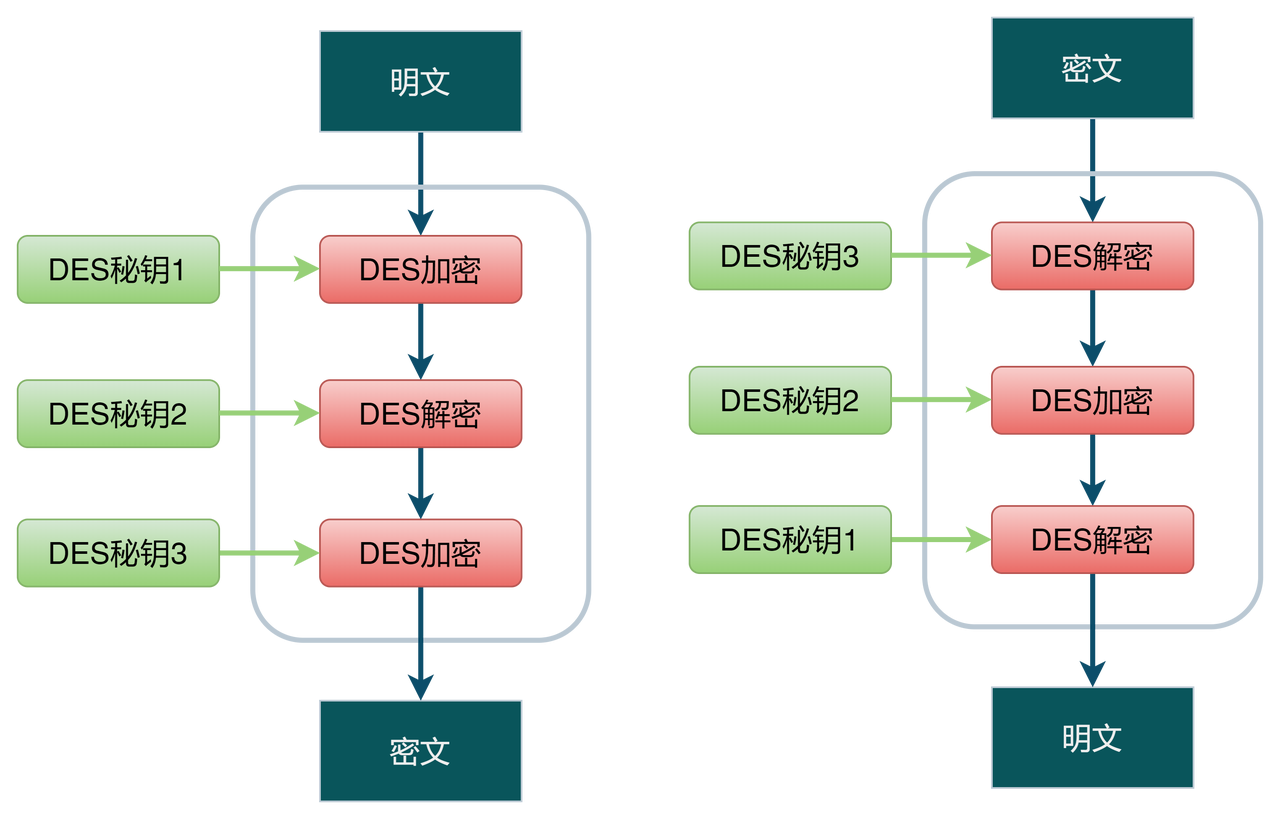
对称加密系统解析
目录 1.概述 2. 对称密码类型 3. 对称加密优缺点 4. 对称加密算法 4.1 DES 4.2 3DES 4.3 AES 4.4 SM1 4.5 SM4 1.概述 对称加密,是指在加密和解密时使用同一秘钥的方式。秘钥的传送和保存的保护非常重要,务必不要让秘…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

