【算法】常用排序算法(插入排序、希尔排序、堆排序、选择排序、冒泡排序、快速排序、归并排序、计数排序)超详细
排序算法是数据结构相关知识中非常重要的一节,相信很多小伙伴对这部分知识一知半解。那么接下来,小编就要带领大家一起来进行对排序算法的深入剖析学习,希望本篇文章能够使你有所收获!
一.常见的排序算法
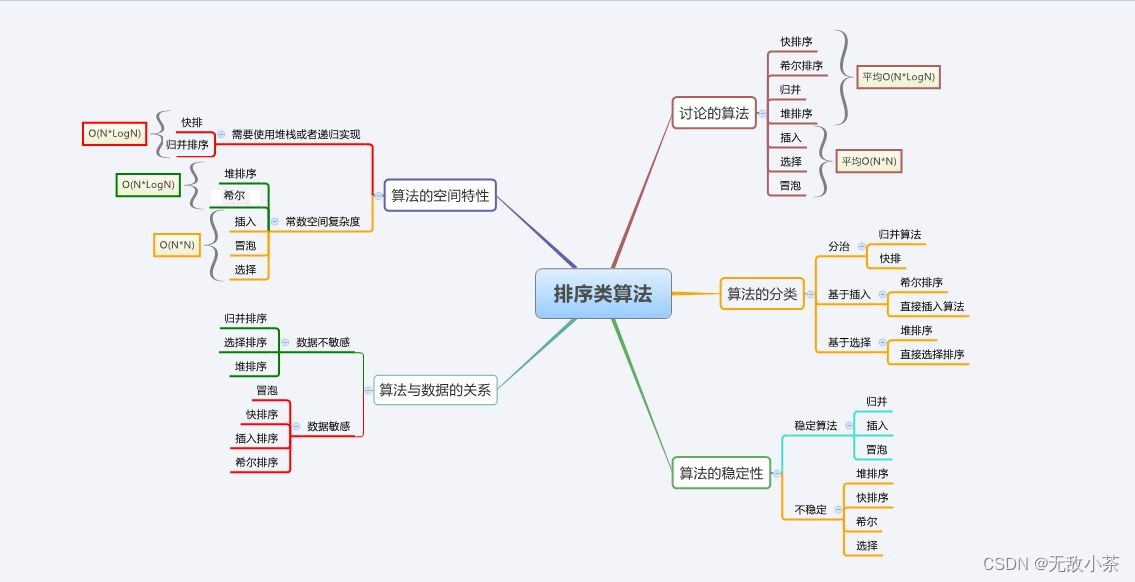
排序算法有很多种,为了使同学们有一个比较系统的了解,小编找了一张图片,用以加深同学们的理解:
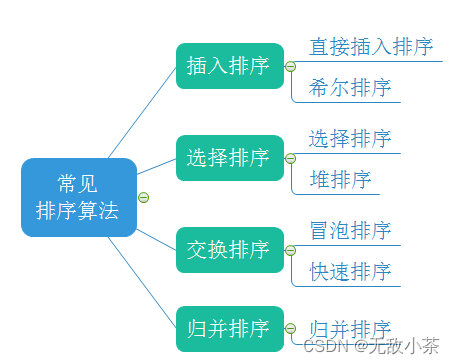
那么接下来,我们就对上图所提到的排序算法进行一一细致的学习吧!
二..插入排序
插入排序,就是把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。
我们平时玩扑克牌,就是运用到了插入排序的思想。
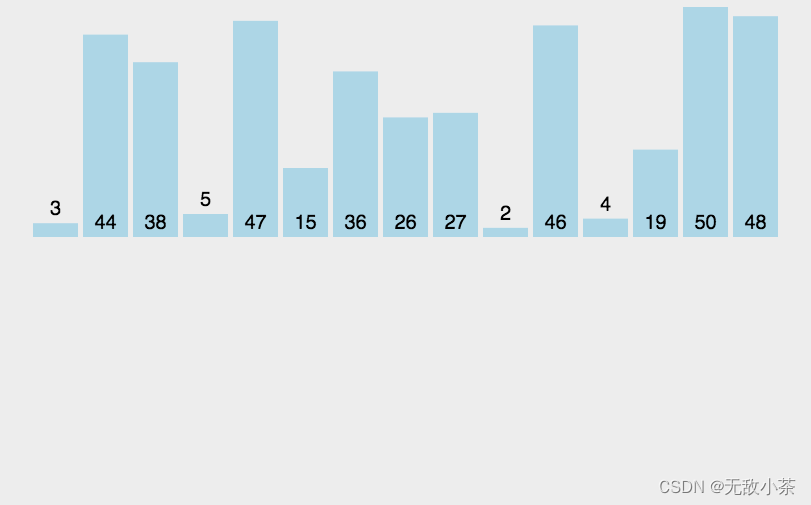
代码展示:
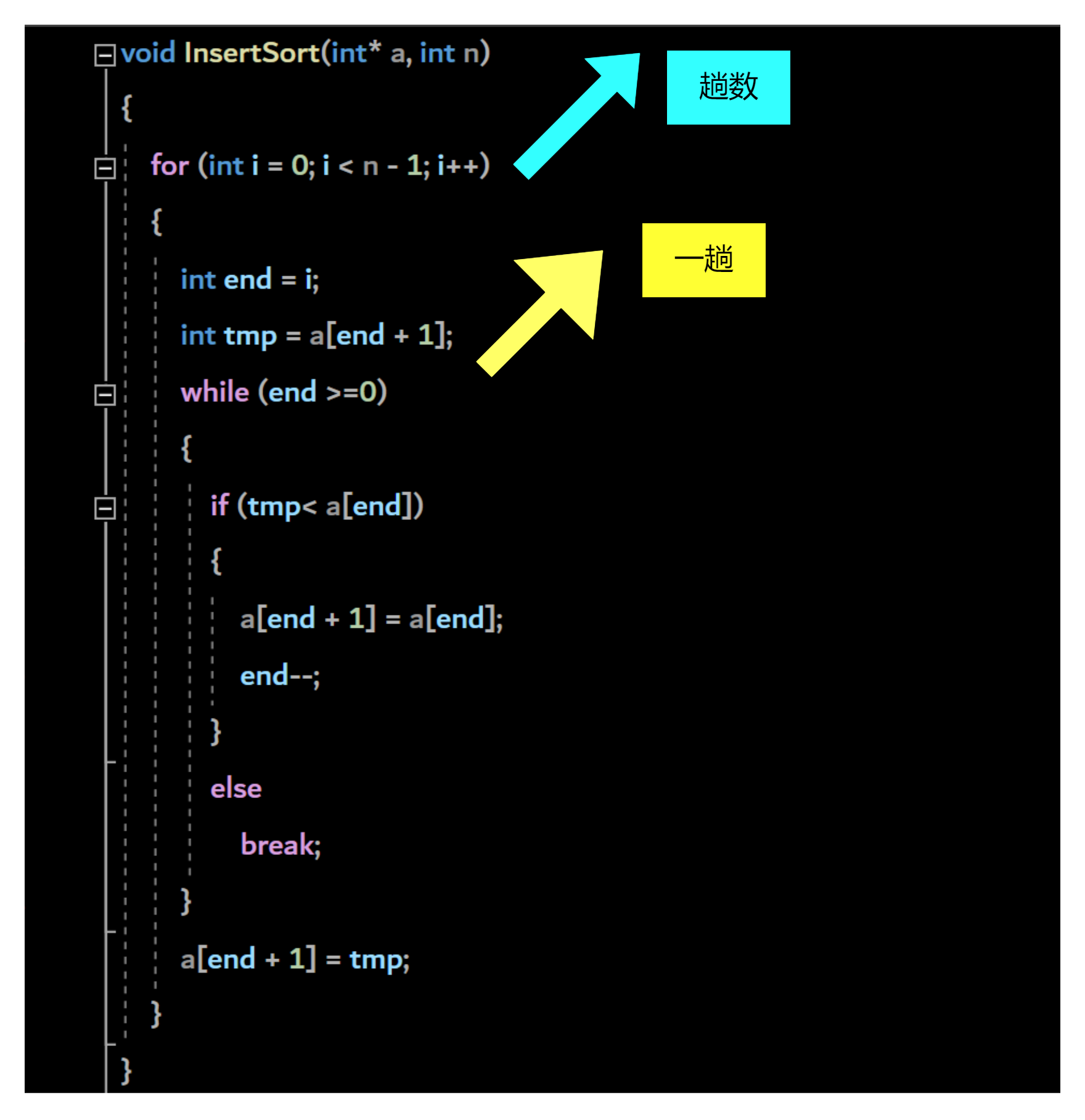
时间复杂度问题:
插入排序最好的时间复杂度是O(N) (当数组元素顺序时)
最坏时间复杂度是是O(N^2) (当数组元素逆序时)
三.希尔排序
只有掌握好插入排序,才会有可能掌握希尔排序。希尔排序是建立在插入排序的基础之上。
希尔排序分为两步:1.预排序(让数组接近有序 注意预排序是多次)
2.插入排序
其中,预排序是将数组分为gap组,每一组中的数是原数组间隔了gap个数而划分的,间隔为gap,亦将数组划分为gap组。
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就 会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
代码展示:

为了方便同学们理解代码,老师做了详细的批注:
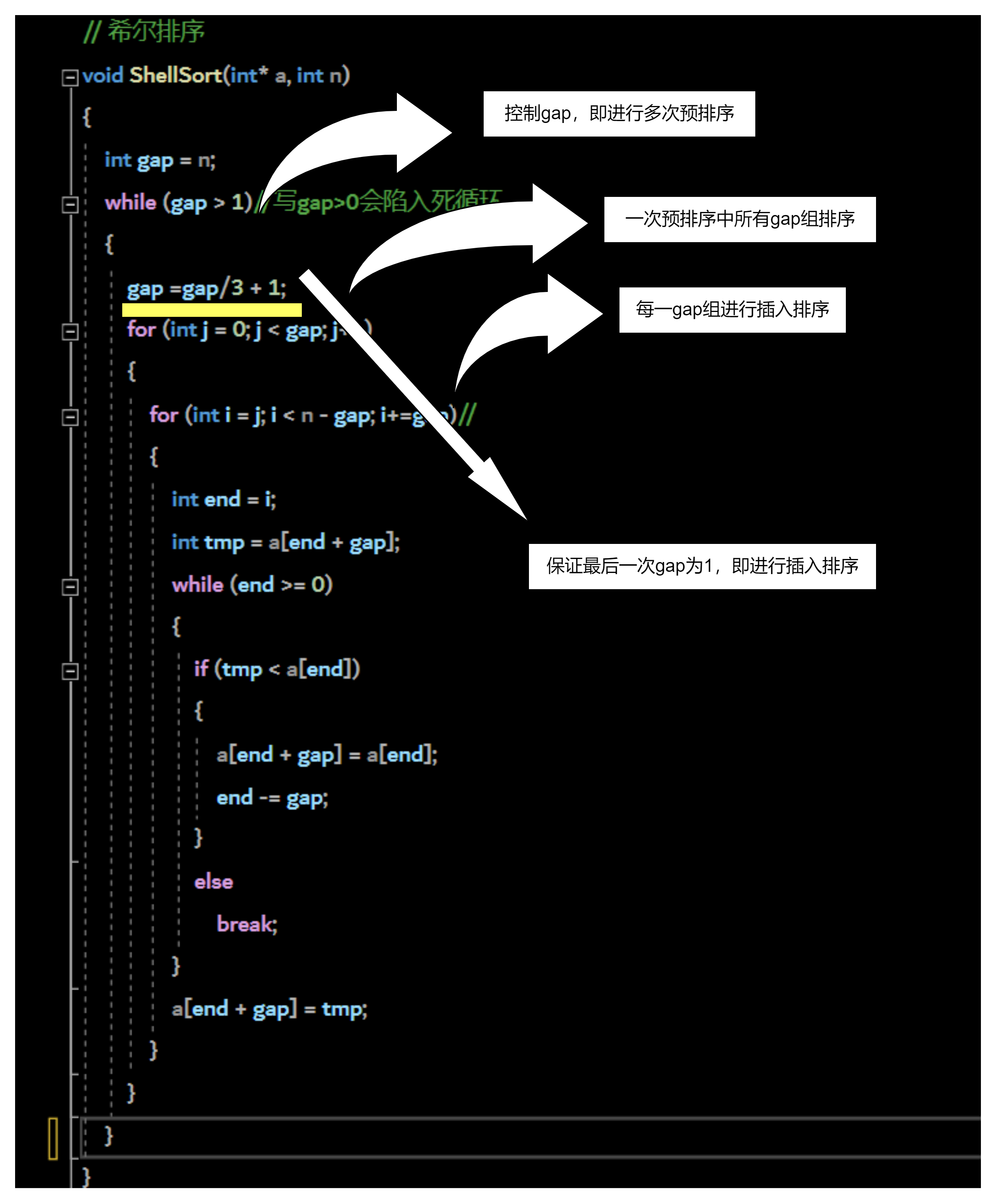
时间复杂度问题分析:
希尔排序的复杂度问题分析非常复杂,我们不做过多研究,我们只告诉大家希尔排序的平均时间复杂度:
O(N^1.3)
四.堆排序
堆排序相信大家都不陌生,早在堆的实现中,我们就已经涉及到了堆的相关知识,那么我们就一起来温习一下吧!
堆排序包括两步:
1.向下调整建堆
2.堆排序
代码展示: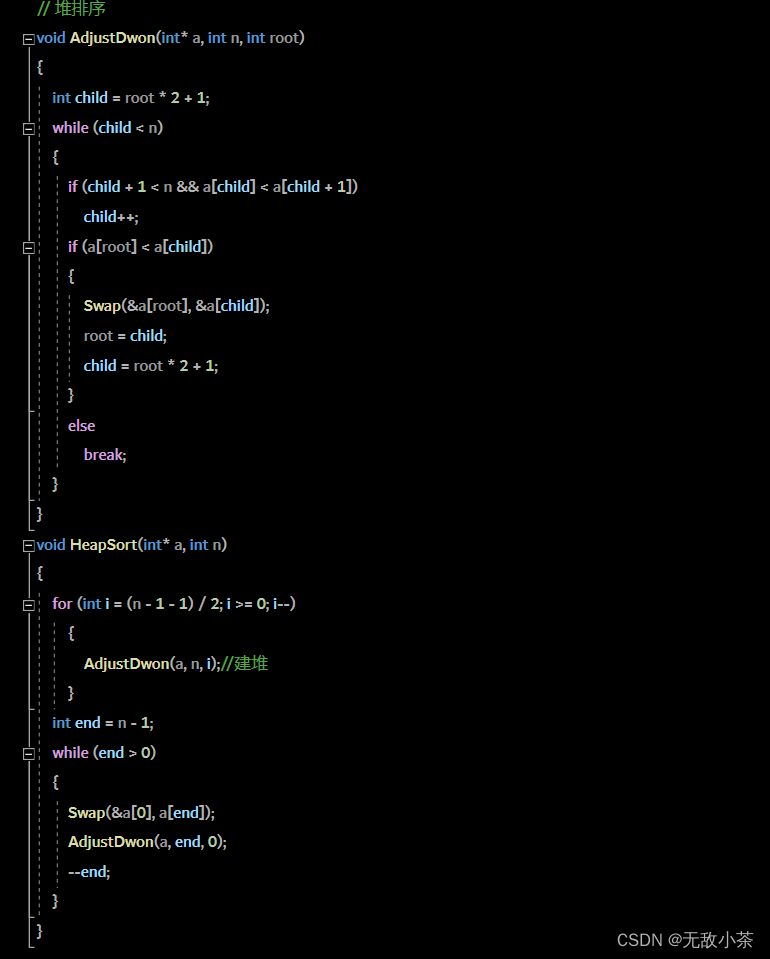
堆排序示意图:
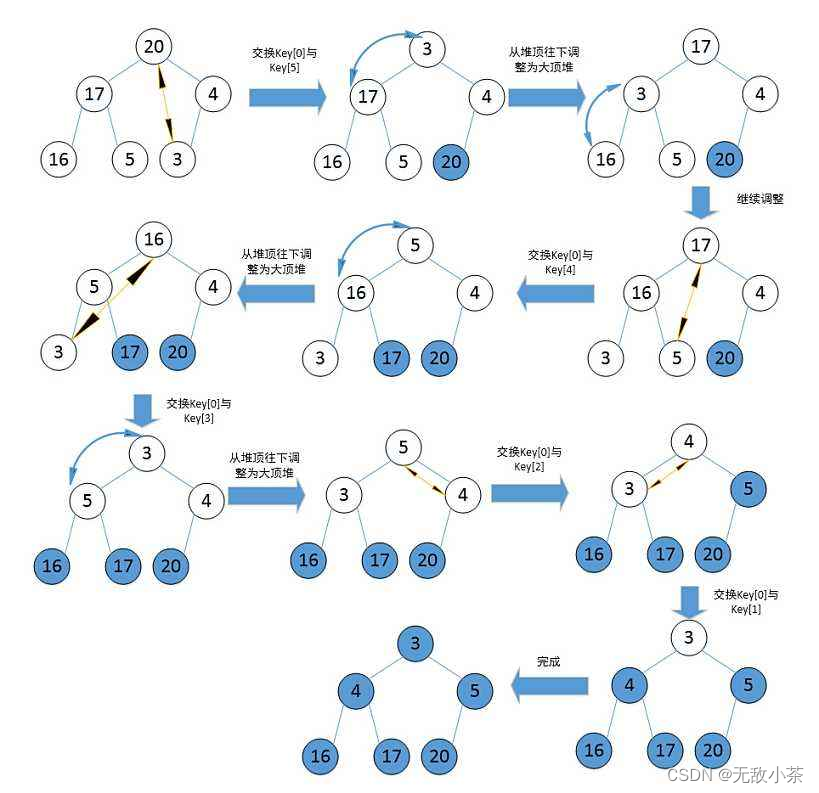
(注意:升序建大堆 降序建小堆 本代码建的是大堆 堆排序具有实践意义,堆排序使用堆来选数,效率就高了很多。)
堆排序时间复杂度:
O(N*logN)
五.选择排序
每一次从待排序的数据元素中选出最小(或/和 最大)的一个元素,存放在序列的起始位置,直到全部待排序的 数据元素排完 。
代码展示:
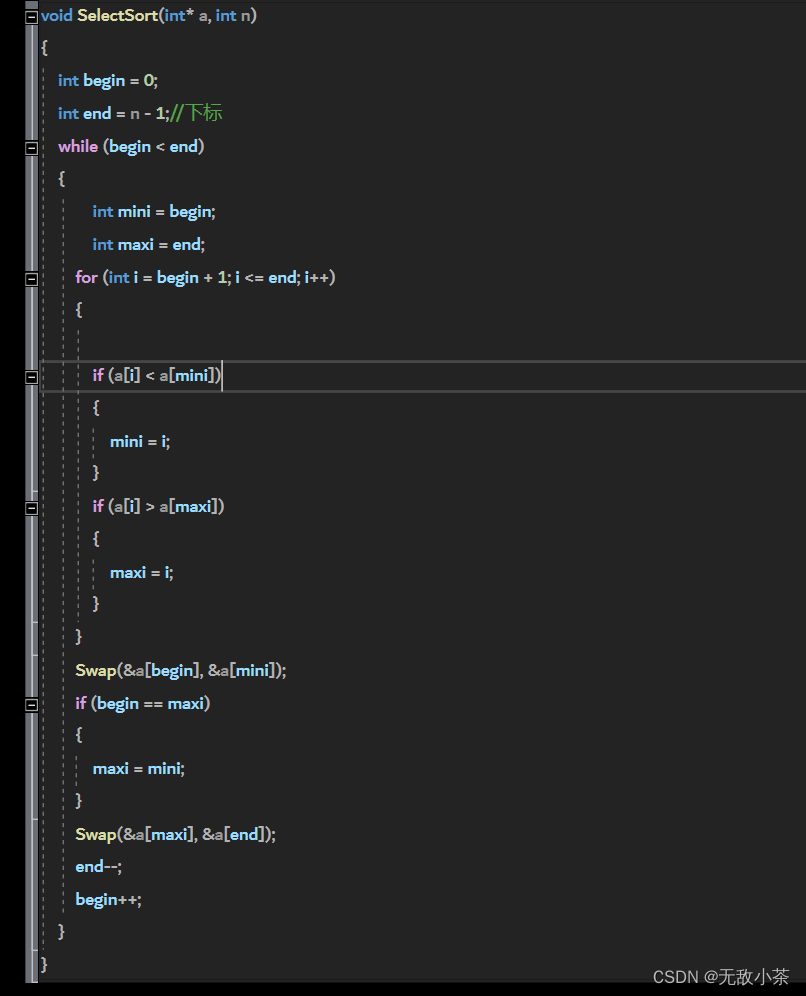
时间复杂度:
O(N^2)
本代码是优化后的选择排序的代码,我们直接同时寻找最小和最大的两个元素,分别放在序列的最左边和最右边。
六.冒泡排序
冒泡排序相信大家都不陌生,那么话不多说,我们直接上代码来展示一下:
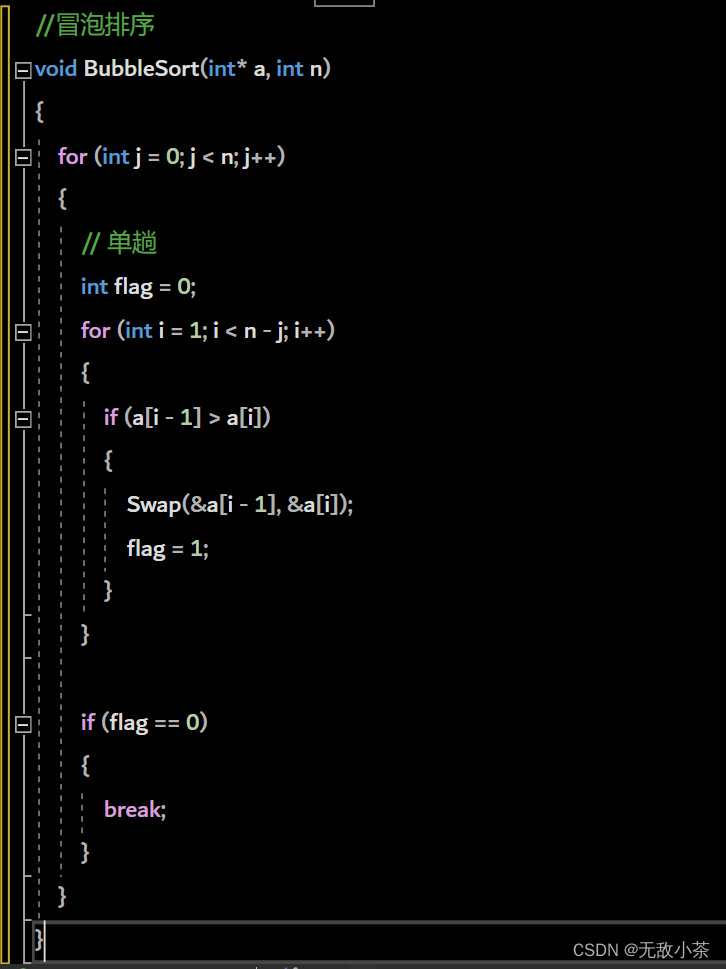
这里我们展示的代码是优化版本的冒牌排序(设立了flag 放置有序情况下效率降低)
冒泡排序的时间复杂度:
最坏情况下时间复杂度:O(N^2)
最好情况下时间复杂度:O(N) (数组顺序)
七.快速排序
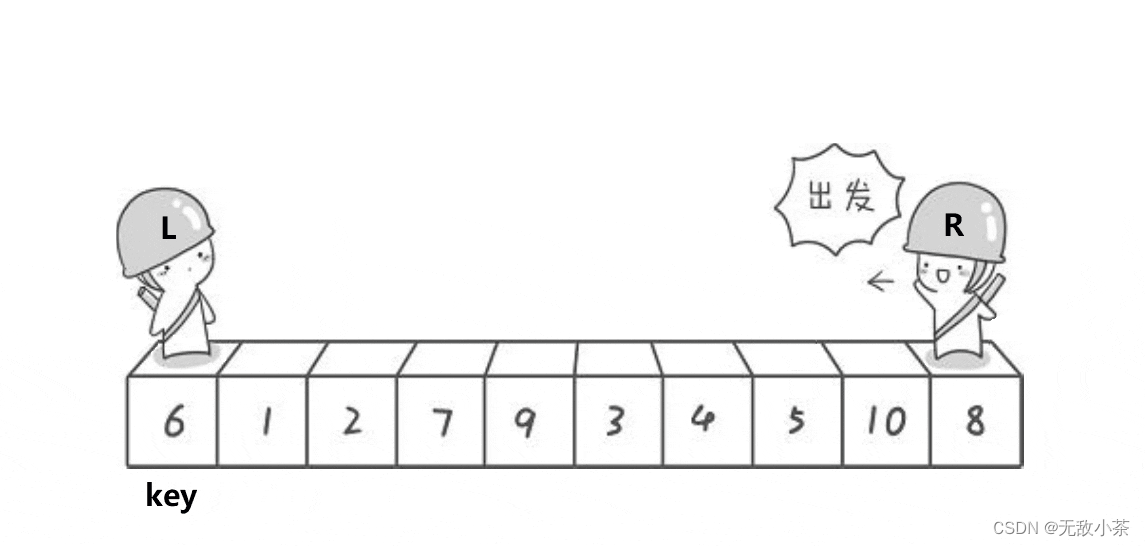
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:
任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
(一)递归算法
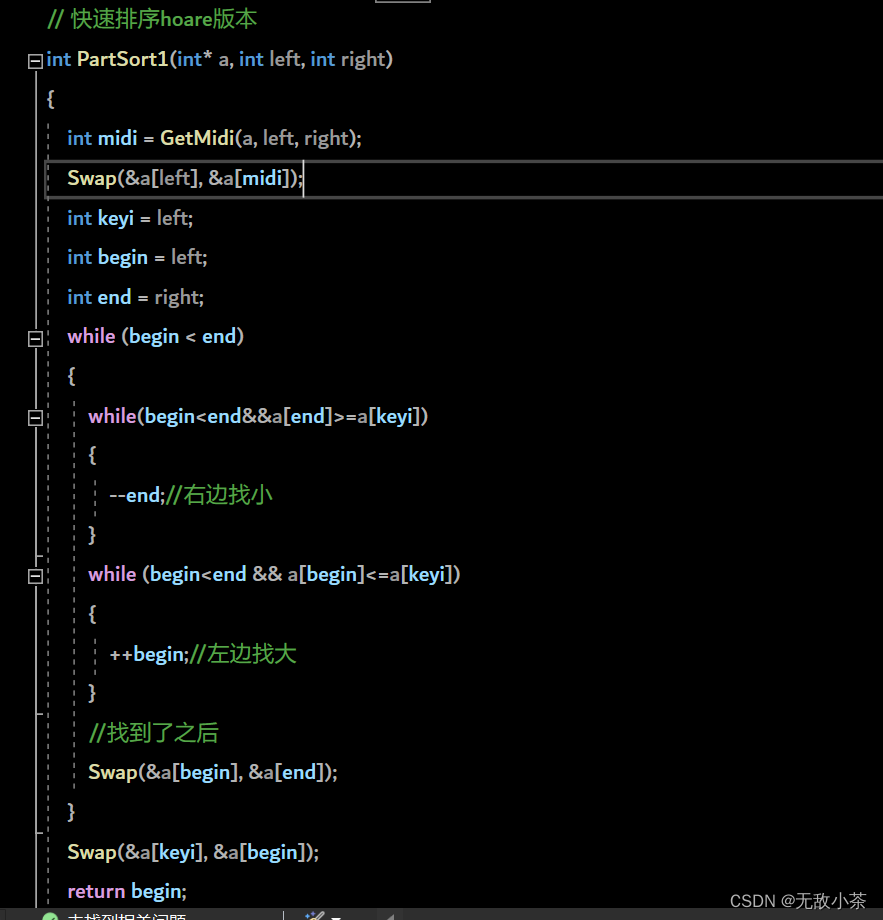
(1).霍尔版本
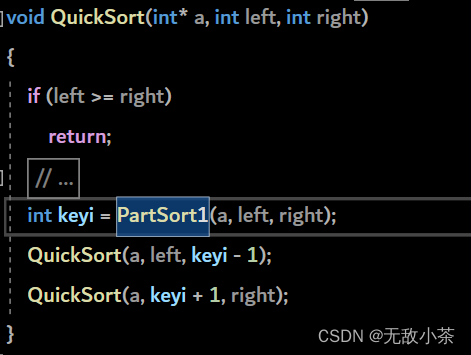
代码展示:
(2).挖坑法
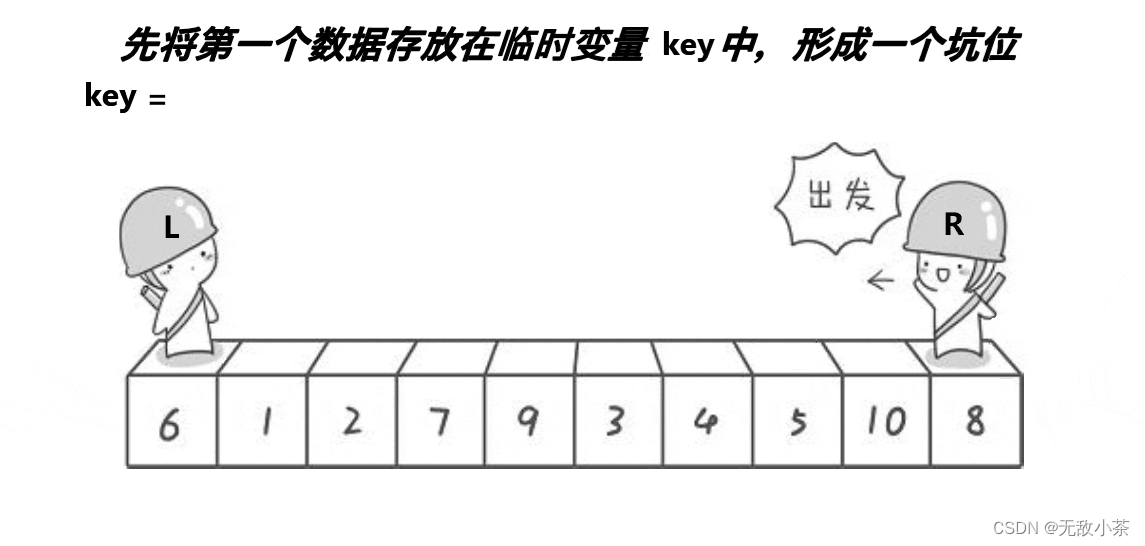
代码展示:
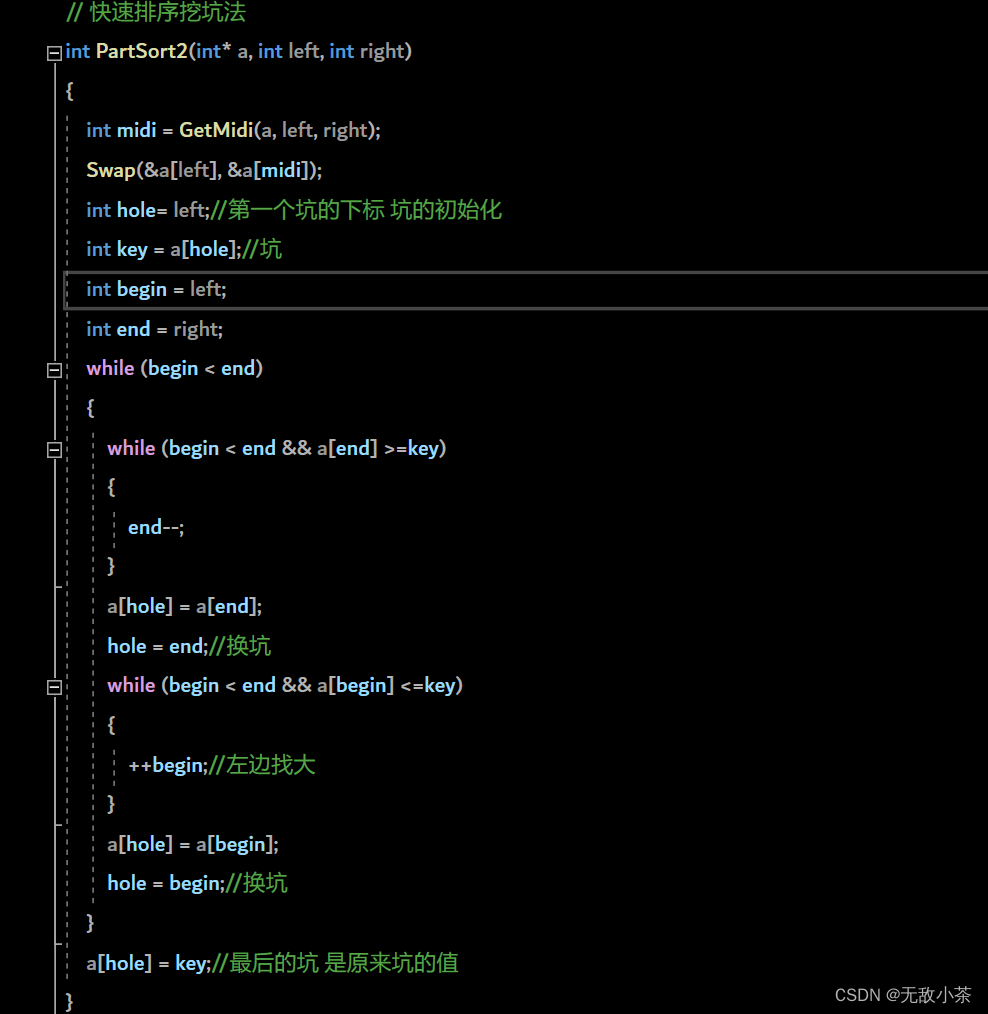
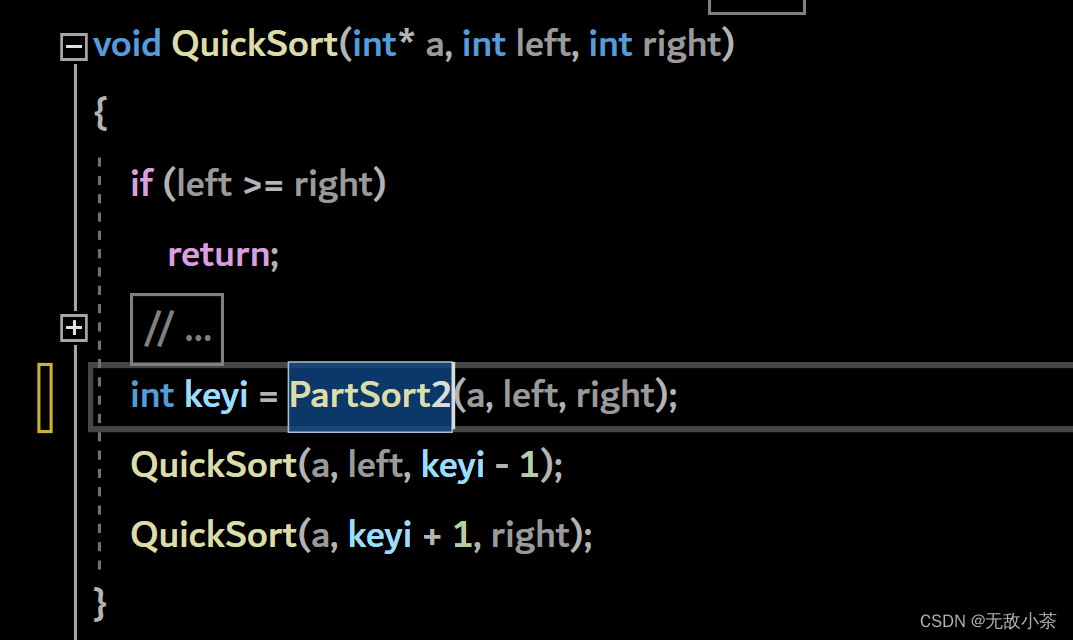
(3).前后指针法

代码展示:
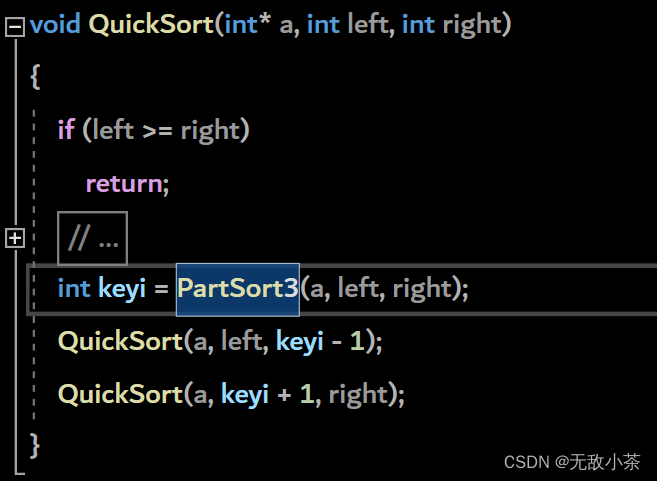
快速排序的时间复杂度:
O(NlogN) (每一层的次数N*层数logN)
注意:
以上代码均是优化后的快速排序算法。快速排序算法的优化:
1.三数取中选择keyi值(避免有序情况下效率退化)(O(N*N)
2.小区间递归优化(当要排序个数小于10时,我们可以采用插入排序。其目的是不再进行递归分割,减小递归深度,防止溢出。)
(二)非递归算法
光是掌握快速排序的递归算法是远远不够的,我们还需要掌握它的非递归算法: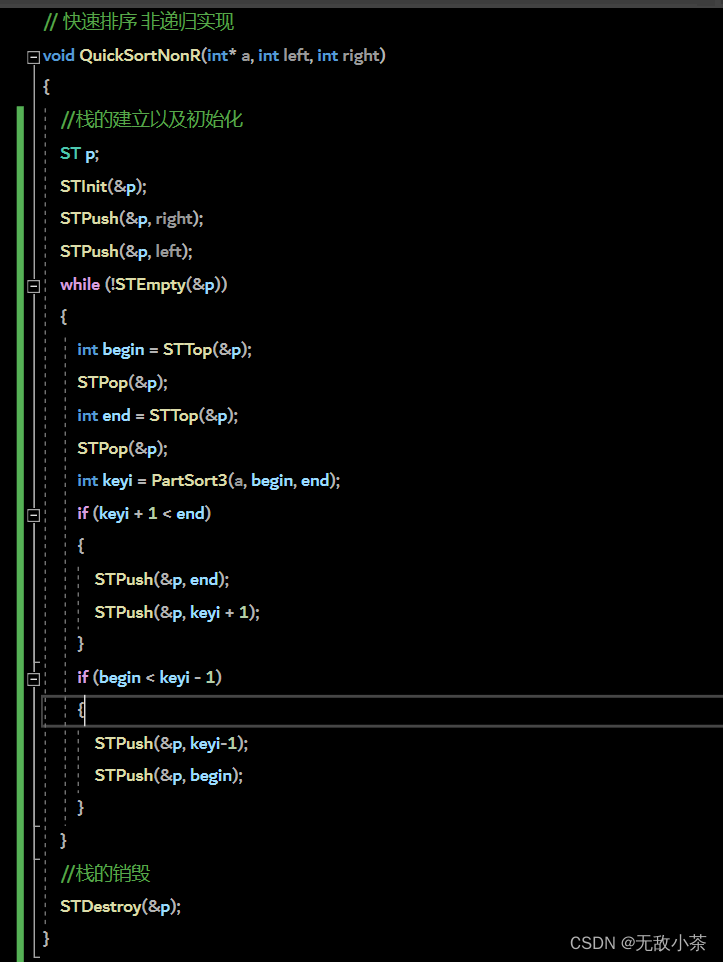
我们借助栈实现了快速排序的非递归算法。
八.归并排序
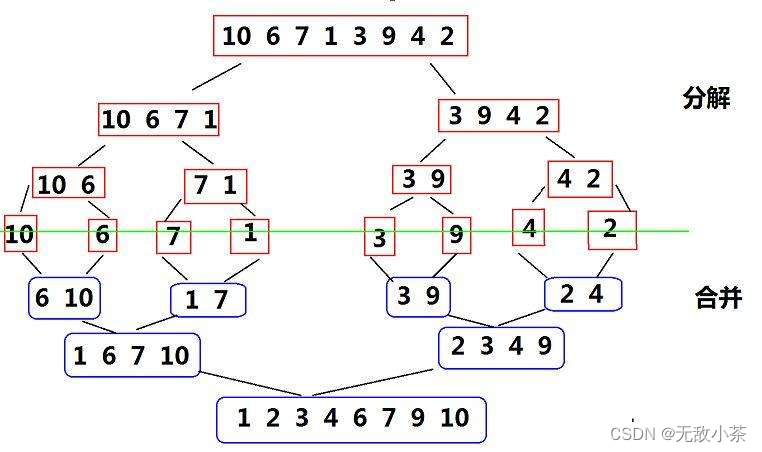
归并排序,简而言之,我们将其总结为“分而治之”。分,即将待排数组分成一个个有序的序列,治,即排序,将这些有序的序列合并,得到完全有序的数组。
(一)递归算法
相信借助下图你可以对归并排序有一个更深入的理解:
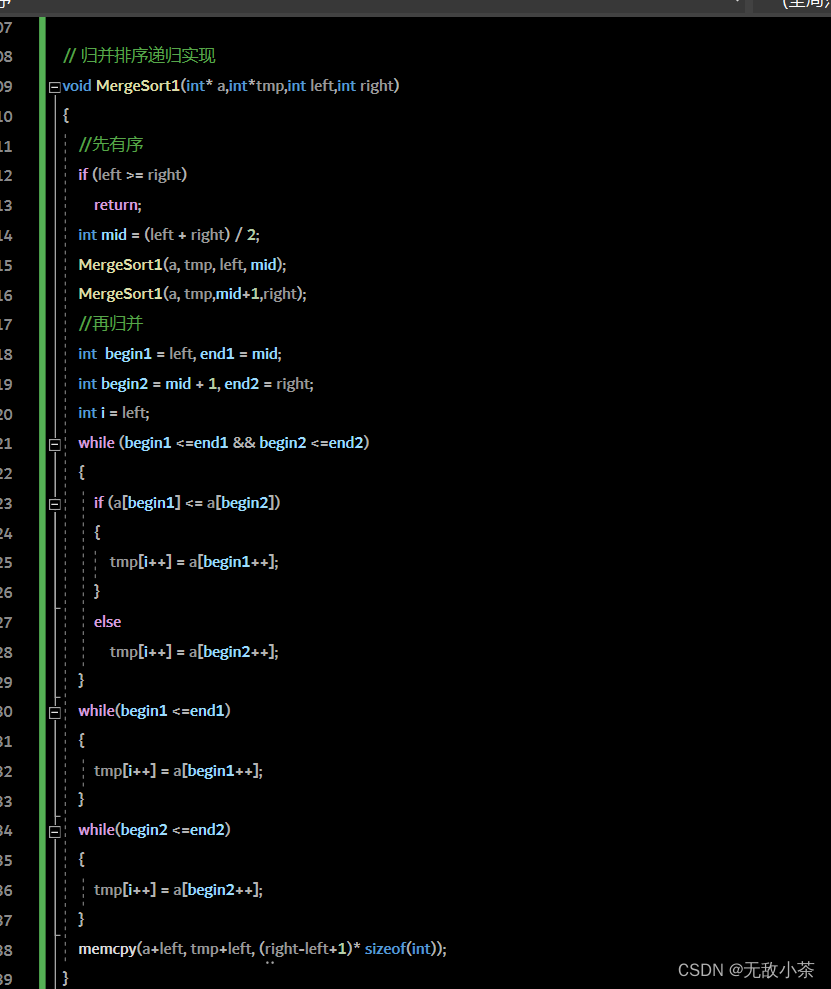
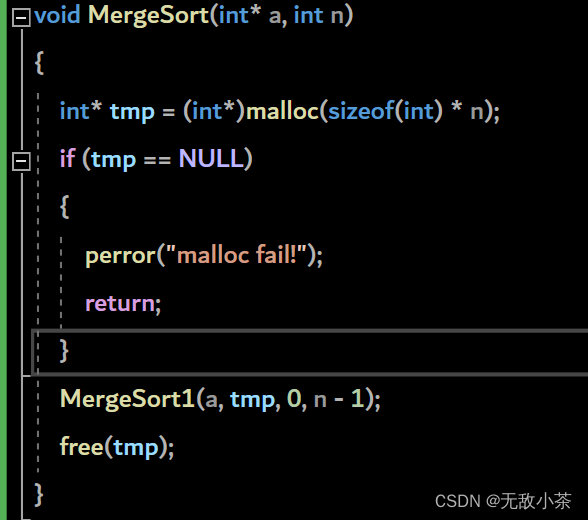
代码展示:
归并排序的时间复杂度分析:
O(N*logN) (每一层的次数N*层数logN)
归并排序的空间复杂度:
O(N) (开辟了一个tmp数组)
(二)非递归算法
我们可以借助栈来实现归并排序的非递归算法: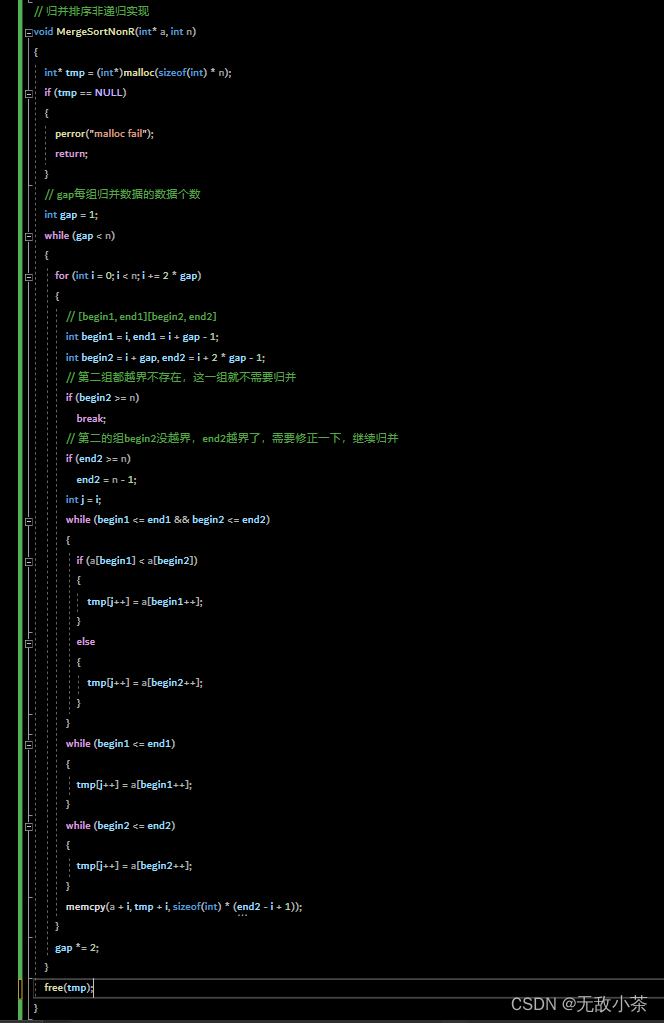
注意:这里要谨防数组边界越界问题。
九.计数排序
计数排序是非比较排序的一种,它的实现原理非常的巧妙。
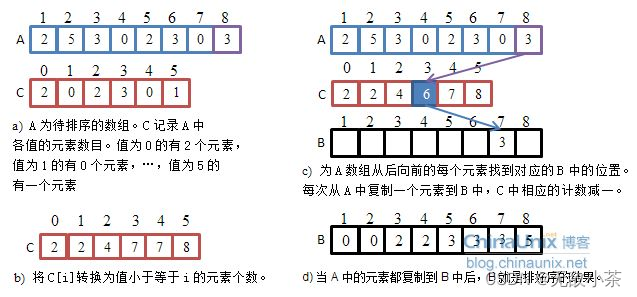
1.建立count数组,统计元素出现的次数
2.根据元素出现的次数回馈到原数组(排序)
代码展示:
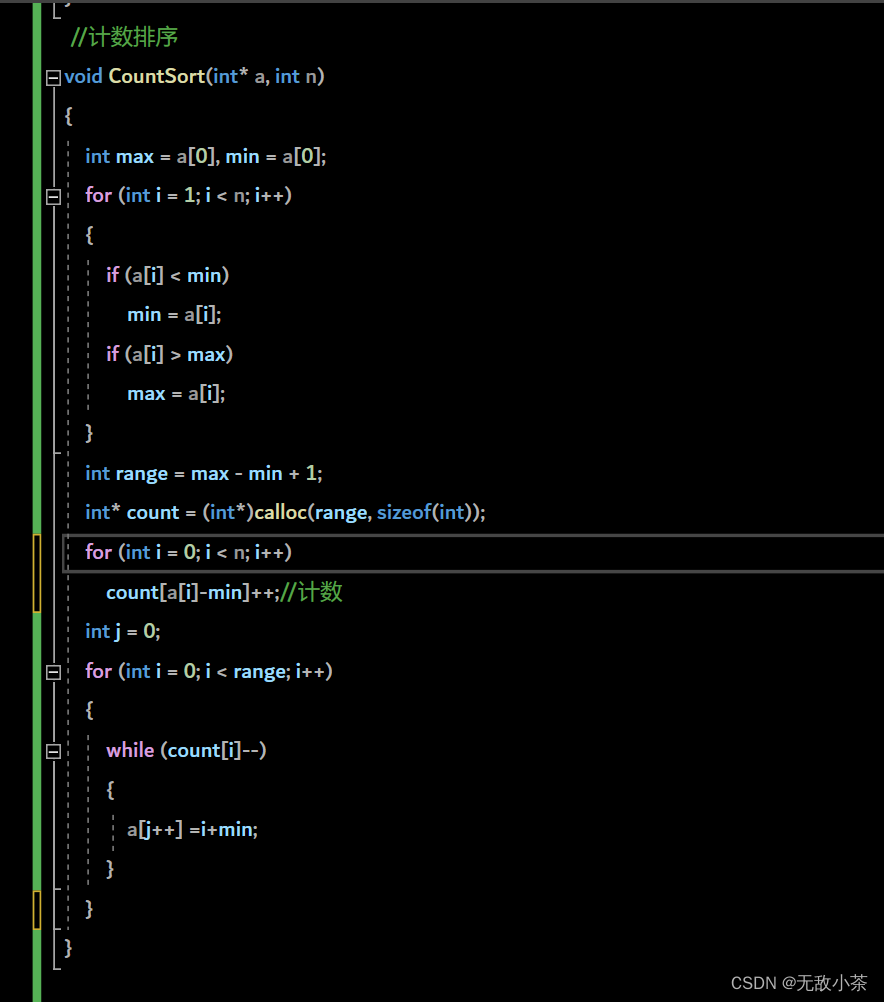
本着减少空间浪费的原则,本代码采用了相对映射的方法。即设立一个range变量。在计数的时候,count的下标写为a[i]-min,在排序的时候,a[j]的值赋值为i+mi。count的下标存储的就是数值。
计数排序适用于数据较为集中且数据为整数的情况。
计数排序的时间复杂度:
O(MAX(range,N))
计数排序的空间复杂度:
Q(N) (开辟了一个数组用以计数)
十.排序算法的稳定性分析
稳定性:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
那么下面这个表格可以帮你快速梳理一下排序算法的相关性质:
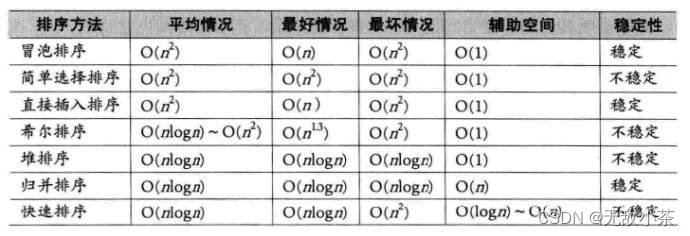
今天关于排序算法的讲解就到这里,相信坚持学习到这里的小伙伴一定收获满满!如果有相关问题,欢迎大家私信留言!小编一定竭尽所能为大家指点迷津!我们下次再会!
相关文章:

【算法】常用排序算法(插入排序、希尔排序、堆排序、选择排序、冒泡排序、快速排序、归并排序、计数排序)超详细
排序算法是数据结构相关知识中非常重要的一节,相信很多小伙伴对这部分知识一知半解。那么接下来,小编就要带领大家一起来进行对排序算法的深入剖析学习,希望本篇文章能够使你有所收获! 一.常见的排序算法 排序算法有很多种&#…...
力扣 240.搜素矩阵II
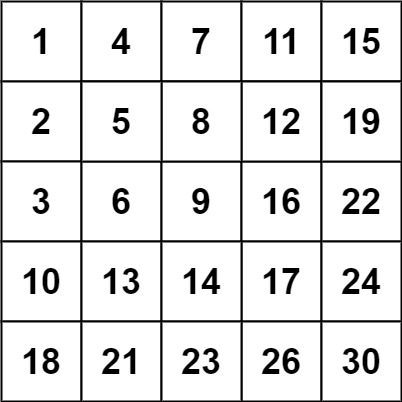
题目描述: 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。每列的元素从上到下升序排列。 示例 1: 输入:matrix [[1,4,7,11,15],[2,5,8,12,19],[3,6,9…...
ASUS华硕ROG幻14Air笔记本GA403UI(UI UV UU UJ)工厂模式原厂Windows11系统安装包,带MyASUS in WinRE重置还原
适用型号:GA403UI、GA403UV、GA403UU、GA403UJ 链接:https://pan.baidu.com/s/1tz8PZbYKakfvUoXafQPLIg?pwd1mtc 提取码:1mtc 华硕原装WIN11系统工厂包带有ASUS RECOVERY恢复功能、自带面部识别,声卡,显卡,网卡,蓝牙等所有驱动、出厂主题…...

Spring Boot通过自定义注解和Redis+Lua脚本实现接口限流
😄 19年之后由于某些原因断更了三年,23年重新扬帆起航,推出更多优质博文,希望大家多多支持~ 🌷 古之立大事者,不惟有超世之才,亦必有坚忍不拔之志 🎐 个人CSND主页——Mi…...

硬件工程师的蜗牛成长路
一名合格的硬件工程师,需要掌握的知识有很多,知识点积累不是一蹴而就,而是细水长流,螺旋提升,不急,慢慢来,想掌握的都能掌握,就让时间来见证个人的成长路径。 ---大青山 2024/6/10 …...
简单记录玩4399游戏flash插件问题
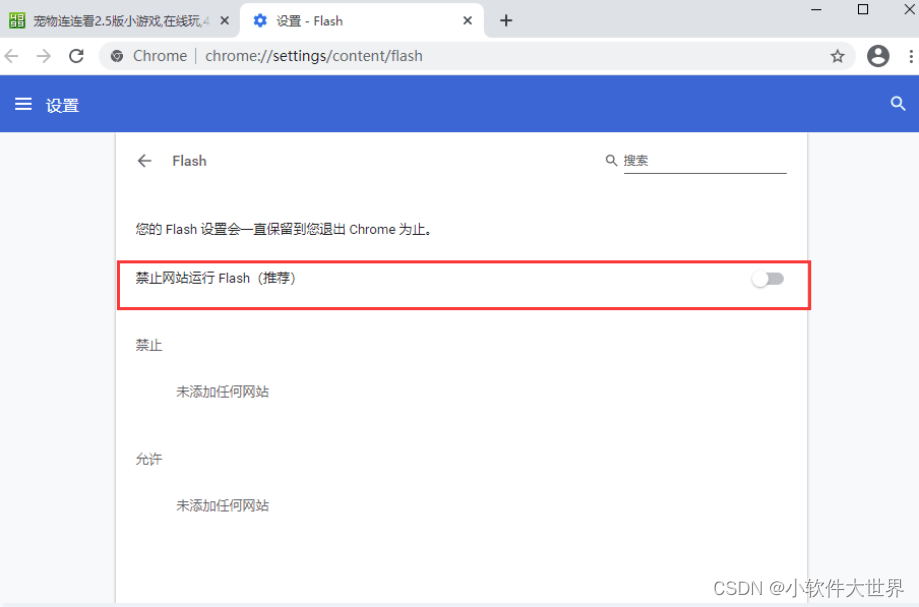
一、因谷歌浏览器默认禁止flash插件自动运行,所以玩家在使用谷歌浏览器,访问www.4399.com平台页面或者4399小游戏(flash资源)时,可能会出现加载异常的情况。今天教大家如何开启flash插件 二、下载falsh官方插件 地址:Flash Player官方下载中心-Flash中国官网 三、如果您…...

GNU/Linux - 使用字符设备来操作GPIO
从 4.8 版开始,Linux 内核引入了基于字符设备的新用户空间 API,用于管理和控制 GPIO(通用输入/输出)。这篇文章介绍了新接口的基本原理,并通过一个简单的教程/示例演示了如何使用新 API 控制 GPIO。 教程中使用的硬件是…...

Android13 Settings 左上角箭头图标点击无效
最近在修改A311D2方案固件,系统Settings发现很多bug 最明显的是左上角有个箭头样子的图标,通常认为是返回键,点击之后没有任何效果,目测这个是ActionBar的按键。 SettingsBaseActivity里面有一段这样的代码: // Th…...
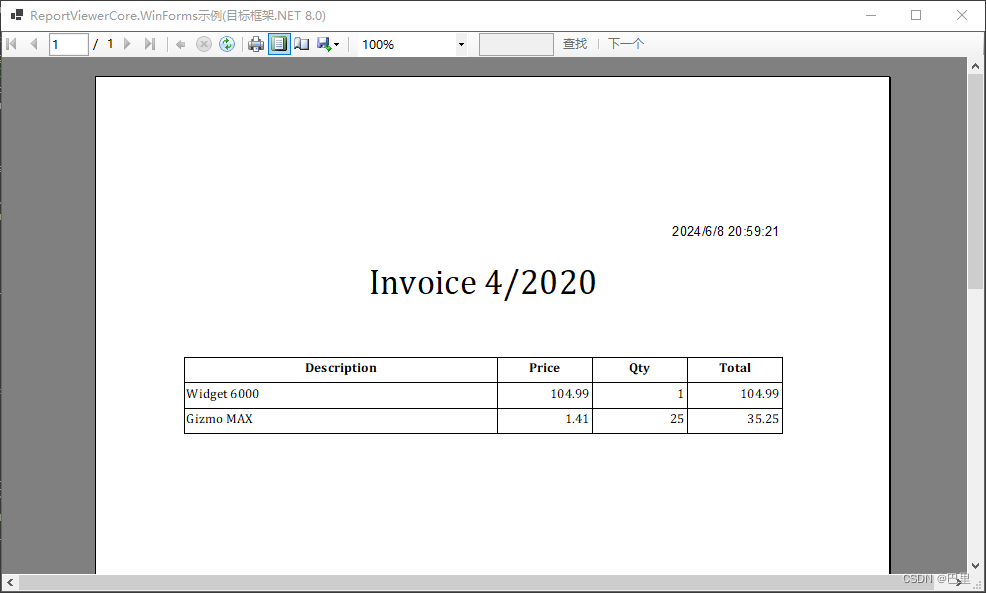
WinForms 应用(.NET 8.0)使用ReportViewerCore.WinForms显示打印RDLC报表
在要WinForms 应用(.NET 8.0)中,显示RDLC报表,就要使用ReportViewerCore.WinForms。原来的ReportViewer只能在.NET Framework框架下运行。 1.ReportViewerCore.WinForms 程序包说明 SQL Server Reporting Services ReportViewer…...
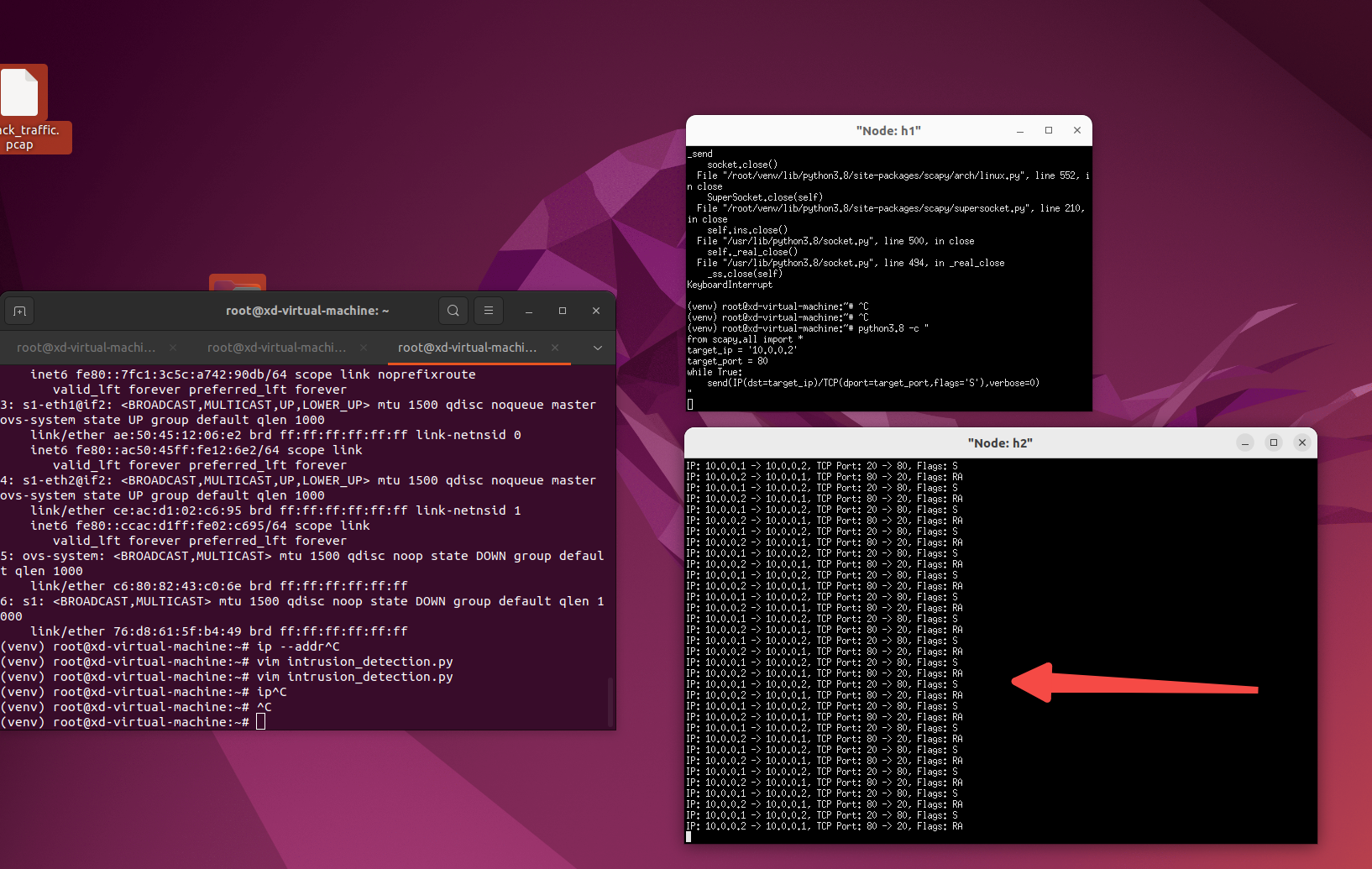
【网络安全】【深度学习】【入侵检测】SDN模拟网络入侵攻击并检测,实时检测,深度学习
文章目录 1. 前言2. Mininet 和 Ryu 的区别2.1 Mininet2.2 Ryu2.3 总结 3. 模拟攻击3.1 环境准备3.2 创建 Mininet 网络拓扑3.2 启动 Ryu 控制器3.3 模拟网络攻击3.4 捕获流量 4. 实时异常检测4.1 在 Ryu 控制器中4.2 在 h2 机器上的实验结果4.3 深度学习模型部署上h2机器 帮助…...

【CentOS】手动编译安装make、cmake、gcc、git
摘要 Centos7升级make和gcc版本到最新——CSDN make make 各个版本下载地址 http://ftp.gnu.org/pub/gnu/make 以4.4为例安装: # 下载 wget https://ftp.gnu.org/pub/gnu/make/make-4.4.tar.gz # 解压配置 tar zxf make-4.4.tar.gz cd make-4.4 ./configure --p…...

45.django - 开始建立第一个项目
1.django是什么? Django是一个高级的、免费的、开源的Web应用框架,它由Python编程语言编写而成。Django遵循模型-视图-控制器(MVC)的设计模式,但通常将其称为模型-视图-模板(MVT)架构。它的主要…...
# 梯影传媒T6投影仪刷机方法及一些刷机工具链接
梯影传媒T6投影仪刷机方法及一些刷机工具链接 文章目录 梯影传媒T6投影仪刷机方法及一些刷机工具链接1、安装驱动程序2、备份设备rom【boot、system】3、还原我要刷进设备的rom【system】4、打开开发者模式以便于安装apk5、root设备6、更多好链接: 梯影传媒T6使用的…...

【代码随想录算法训练营第37期 第三十二天 | LeetCode122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II】
代码随想录算法训练营第37期 第三十二天 | LeetCode122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II 一、122.买卖股票的最佳时机II 解题代码C: class Solution { public:int maxProfit(vector<int>& prices) {int result 0;for(int i 1; i &…...
DP:回文串模型
一、回文子串 . - 力扣(LeetCode) 该题有3种解法 (1)中心扩展算法(在字符串章节有介绍)时间复杂度O(N^2),空间复杂度O(1) (2)马丁车…...

STM32CubeMX软件的安装以及配置
STM32CubeMX软件的配置过程可以详细分为以下几个步骤,以确保您能够顺利地使用该软件进行STM32微控制器的配置和代码生成: 1. 安装前准备 安装JAVA环境:由于STM32CubeMX软件是基于JAVA环境运行的,所以需要先安装Java Runtime Env…...

【适配鸿蒙next】Flutter 新一代混合栈管理框架
前言 据最新消息显示,华为今年下半年将全面转向其自主平台HarmonyOS,放弃Android系统。 报道中提到,下一版HarmonyOS预计将随华为即将推出的Mate 70旗舰系列一起发布。 据悉,HarmonyOS Next 已经扩展到4000个应用程序,…...

车载电子电气架构 --- 车载信息安全
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...
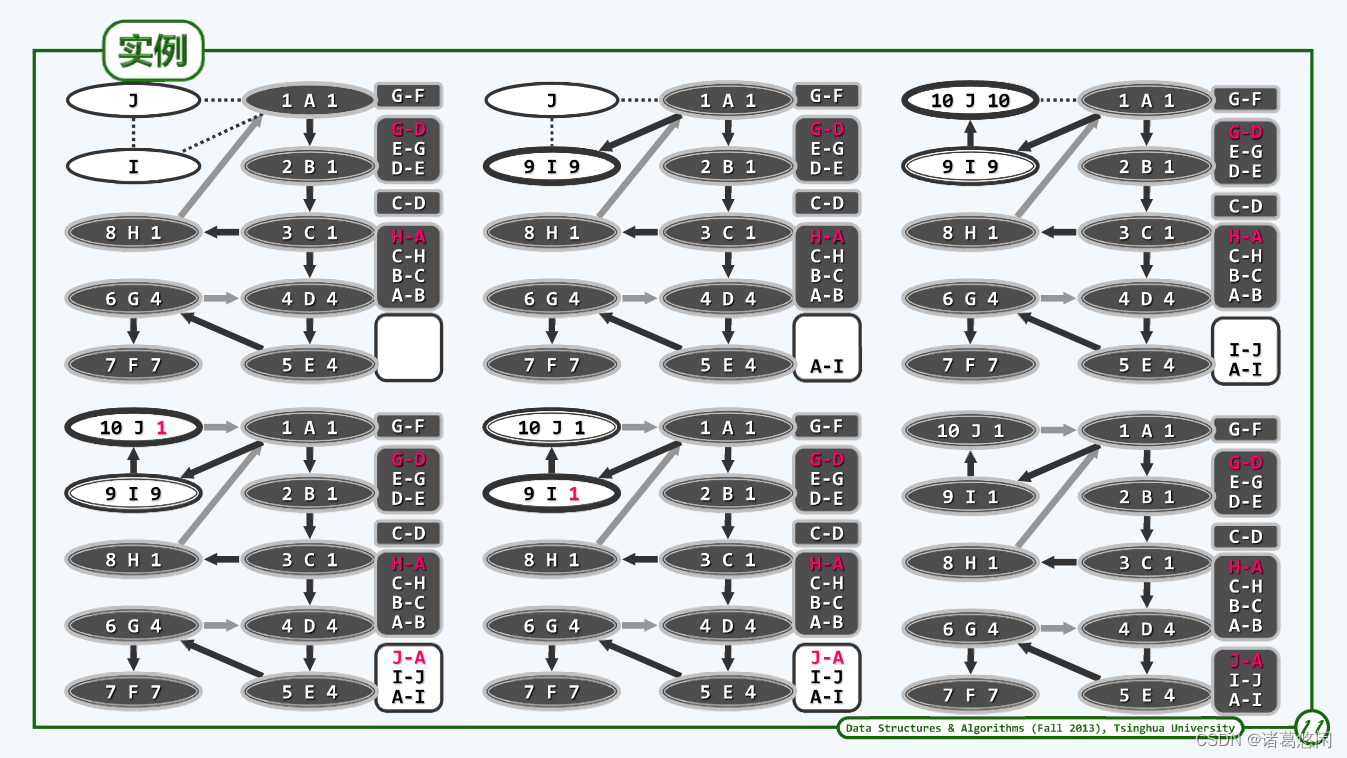
【数据结构(邓俊辉)学习笔记】图04——双连通域分解
文章目录 0. 概述1 关节点与双连通域2 蛮力算法3 可行算法4 实现5 示例6 复杂度 0. 概述 学习下双连通域分解,这里略微有一点点难,这个算是DFS算法的非常非常经典的应用,解决的问题也非常非常有用。 1 关节点与双连通域 连通性很好理解&am…...

UI学习(二)
UI学习(二) 文章目录 UI学习(二)布局子视图手动布局自动布局 导航控制器导航控制器基础导航控制器的切换导航栏工具栏 分栏控制器分栏控制器协议部分的内容UITableView基础部分相关的协议函数高级协议与单元格 多界面传值 布局子视…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...
