数据结构：二叉树的实现

目录

二叉树的遍历方式

  前序遍历：

  中序遍历：

  后序遍历：

二叉树的基本结构和功能

  基本结构：

  基本功能：

二叉树功能的实现思路

二叉树功能的实现

   1、构建一个二叉树

   2、二叉树的销毁

   3、计算二叉树里的节点个数

   4、得到二叉树的子叶节点个数

    5、得到二叉树第K层节点个数

     6、查找二叉树值为X的节点

   7、二叉树的前/中/后序遍历

        前序遍历

        中序遍历

        后序遍历

   8、层序遍历

   9、判断二叉树是否为完全二叉树

---

二叉树的遍历方式

        二叉树有三种遍历方式，不同的遍历方式有不同的效果和作用。（实现二叉树的代码）

  前序遍历：

        根->左子树->右子树。

        (如上图所示)用前序遍历这个二叉树的结果是： 1 2 4 8 5 3 6 9 7

        如果加上空的子树，结果是：1 2 4 N 8 N N 5 N N 3 6 9 N N N 7 N N(为了方便理解，同一种颜色的是根的子树)

---

  中序遍历：

        左子树->根->右子树。

        (如上图所示)用前序遍历这个二叉树的结果是： 4 8 2 5 1 9 6 3 7

        如果加上空的子树，结果是：N 4 N 8 N 2 N 5 N 1 N 9 N 6 N 3 N 7 N(为了方便理解，同一种颜色的是根的子树) 

---

  后序遍历：

        左子树->右子树->根。

        (如上图所示)用前序遍历这个二叉树的结果是： 8 4 5 2 9 6 7 3 1

        如果加上空的子树，结果是：N N N 8 4 N N 5 2 N N 9 6 N N 7 3 1(为了方便理解，同一种颜色的是根的子树) 

---

二叉树的基本结构和功能

  基本结构：

        我们知道二叉树里有一个值和指向两个子树的指针构成，所以我们可以用下面的结构体来作为一个节点。

typedef char BTDataType;//为了便于以后因不同需求而更改。
//节点
typedef struct BinaryTreeNode
{BTDataType _data;//存放值struct BinaryTreeNode* _left;//一个指向左子树的指针struct BinaryTreeNode* _right;//一个指向右子树的指针
}BTNode;

---

  基本功能：

1. 通过一个关于二叉树遍历的字符串来构建出一个二叉树
2. 二叉树的销毁
3. 得到二叉树的节点个数
4. 得到二叉树的子叶节点个数
5. 得到二叉树第K层节点个数
6. 查找二叉树值为X的节点
7. 二叉树的前序遍历
8. 二叉树的中序遍历
9. 二叉树的后序遍历
10. 层序遍历
11. 判断二叉树是否为完全二叉树

---

二叉树功能的实现思路

        （二叉树的大部分功能的实现都需要用到递归，所以我们要对递归一定熟练度）当我们要构建一个二叉树的时候，可以用递归的方式来连接一个一个的节点。其他的功能最主要的也是用递归

实现的。

---

二叉树功能的实现

   1、构建一个二叉树

        当我们要构建一个二叉树，我们首先要确定它的构建方式——前序、中序还是后序。（这里以前序遍历为例）

        前序遍历的方式是根->左子树->右子树。

        若我们要通过前序遍历的数组" A B D # # E # H # # C F # # G # # "构建二叉树，我们首先可以先画出构建好的二叉树的图形(如下图所示)，这回让你对你要创建的二叉树有更深的理解。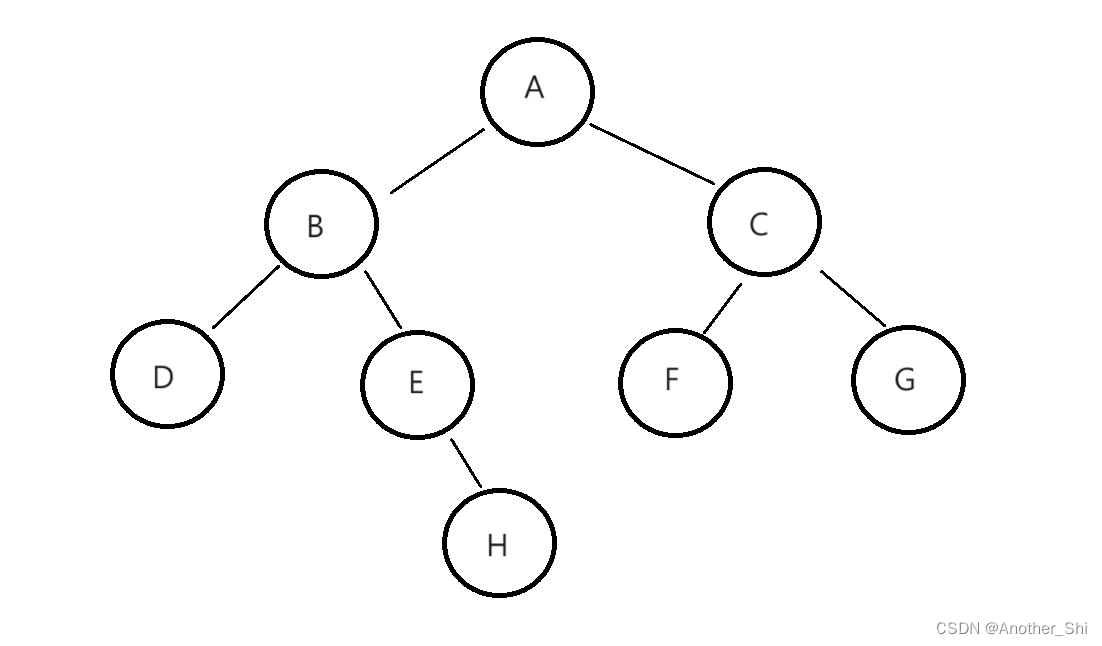

         利用递归的性质，我们只要遇到 ' # '就返回，反之，就创建节点，然后使其链接左子树和右子树。

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{//当遇到' # '就返回if (a[*pi] == '#'){(*pi)++;return NULL;}//创建一个节点BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");return NULL;}root->_data = a[*pi];(*pi)++;root->_left = BinaryTreeCreate(a, pi);//链接左子树root->_right = BinaryTreeCreate(a, pi);//链接右子树//最后返回根return root;
}

        如果我们想要用其他的遍历方式来构建二叉树可以调整一下链接左子树的时机。(记得字符串里的内容要是对应的遍历方式)

---

   2、二叉树的销毁

        要销毁一个二叉树，我们首先要确定销毁方式，因二叉树的结构只能用后序遍历(左子树->右子树->根)的方式来销毁二叉树。

        假如我们用前序(左子树->根->右子)或中序(左子树->根->右子树)的方式销毁二叉树，我们都会先销毁根，导致我们找不到后续的子树，所以我们只能用后序的方式来销毁二叉树。

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}//先遍历到子叶再开始销毁BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*root);*root = NULL;
}

---

   3、计算二叉树里的节点个数

        计算节点个数，我们只需要遇到空指针就返回，反之就加左子树和右子树之和再加1（本身）即可。

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

---

   4、得到二叉树的子叶节点个数

        遇到空就返回0，如果本身非空且有左子树则加1，如果本身非空且有右子树则加1，这样我们就可以得到二叉树的子叶节点个数了。

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root && root->_left == NULL)return 1;if (root && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

---

    5、得到二叉树第K层节点个数

        我们先设根节点为第一层，则第二层就为k-1层，然后推导，当k == 1的时候就是我们需要计算节点个数的层数。若该二叉树没有第k层呢？我们只需当k == 0时就返回0即可。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;//当k == 1时就返回1if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

---

     6、查找二叉树值为X的节点

        在二叉树里查找一个值的时候，我们首先要确定查找方式，(这里以前序为例)，我们用前序查找，如果左子树有这个值就返回该节点，没有就返回NULL，然后再查找右子树，若也没有就返回NULL。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* left = BinaryTreeFind(root->_left, x);return left != NULL ? left : BinaryTreeFind(root->_right, x);
}

        如果不在左子树，那就只有两种可能，一个是在右子树，一个是没有这个值。这里的left都为空的话，那只能去右子树里去找了。

---

   7、二叉树的前/中/后序遍历

        这三种遍历方式在二叉树的实现都差不多，只是要区分先后顺序。

        前序遍历

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){	printf("# ");return;}printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

        中序遍历

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}BinaryTreePrevOrder(root->_left);printf("%c ", root->_data);BinaryTreePrevOrder(root->_right);
}

        后序遍历

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%c ", root->_data);
}

---

   8、层序遍历

        层序遍历就与上面的遍历有所不同，这里我们要利用队列来存储节点的指针来达到层序遍历。

        这里的层序遍历的结构是：A B C D E F G H 

        首先，我们要清楚队列的性质，队列是由链表构成，先进先出的方式来进出队列。开始先入一个根节点，每当出一个二叉树的节点就得要入它的左子树节点和右子树节点。遇到不是空节点就入队列。这样我们就可以实现二叉树的层序遍历。(这里避免过于臃肿就不写队列的过程了，如果想了解一下队列可以看看这篇文章详解栈和队列的实现以及它们的相互实现)

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if(root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%c", front->_data);if(front->_left)QueuePush(&q, front->_left);if (front->_right)QueuePush(&q, front->_right);QueuePop(&q);}printf("\n");
}

---

   9、判断二叉树是否为完全二叉树

        判断二叉树是否为完全二叉树的实现，跟上面基本同理，当与到空的时候就直接break去判断后面还有没有其他的数，无，则是完全二叉树，反之，不是完全二叉树。

        原理：(将空指针视为 N )如果一个二叉树是完全二叉树，将像上面入队列的时候，队列中存储的数据到N的时候后面就只有N了。但如果还有其他的数，那就不可能是完全二叉树。

// 判断二叉树是否是完全二叉树
bool BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if(root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if( front == NULL)break;if(front->_left)QueuePush(&q, front->_left);if (front->_right)QueuePush(&q, front->_right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if( front){QueueDistory(&q);return false;}}   return true;
}

(完)