33、matlab矩阵分解汇总:LU矩阵分解、Cholesky分解和QR分解
1、LU矩阵分解
语法
语法1:[L,U] = lu(A) 将满矩阵或稀疏矩阵 A 分解为一个上三角矩阵 U 和一个经过置换的下三角矩阵 L,使得 A = L*U。
语法2:[L,U,P] = lu(A) 还返回一个置换矩阵 P,并满足 A = P'*L*U。
语法3:[L,U,P] = lu(A,outputForm) 以 outputForm 指定的格式返回 P。
1)矩阵的 LU 分解
代码及运算
A = [8 -7 0-4 0 65 -1 9];
[L,U] = lu(A)
L*UL =1.0000 0 0-0.5000 1.0000 00.6250 -0.9643 1.0000U =8.0000 -7.0000 00 -3.5000 6.00000 0 14.7857ans =8 -7 0-4 0 65 -1 9代码及运算
[L,U,P] = lu(A)
P'*L*UL =1.0000 0 0-0.5000 1.0000 00.6250 -0.9643 1.0000U =8.0000 -7.0000 00 -3.5000 6.00000 0 14.7857P =1 0 00 1 00 0 1ans =8 -7 0-4 0 65 -1 92)用 LU 分解对线性系统求解
A = magic(5);
b = 65*ones(5,1);
x = A\b
[L,U,P] = lu(A)
y = L\(P*b);
x = U\y
dA = decomposition(A,'lu');
x = dA\bx =1.00001.00001.00001.00001.0000L =1.0000 0 0 0 00.7391 1.0000 0 0 00.4783 0.7687 1.0000 0 00.1739 0.2527 0.5164 1.0000 00.4348 0.4839 0.7231 0.9231 1.0000U =23.0000 5.0000 7.0000 14.0000 16.00000 20.3043 -4.1739 -2.3478 3.17390 0 24.8608 -2.8908 -1.09210 0 0 19.6512 18.97930 0 0 0 -22.2222P =0 1 0 0 01 0 0 0 00 0 0 0 10 0 1 0 00 0 0 1 0x =1.00001.00001.00001.00001.0000x =1.00001.00001.00001.00001.00002、Cholesky 分解:chol Cholesky 分解
语法
语法1:R = chol(A) 将对称正定矩阵 A 分解成满足 A = R'*R 的上三角 R。
语法2:R = chol(A,triangle) 指定在计算分解时使用 A 的哪个三角因子。
语法3:[R,flag] = chol(___) 还返回输出 flag,指示 A 是否为对称正定矩阵。
1)矩阵的 Cholesky 分解
代码及运算
A = gallery('lehmer',6);
R = chol(A)
norm(R'*R - A)
L = chol(A,'lower')
norm(L*L' - A)R =1.0000 0.5000 0.3333 0.2500 0.2000 0.16670 0.8660 0.5774 0.4330 0.3464 0.28870 0 0.7454 0.5590 0.4472 0.37270 0 0 0.6614 0.5292 0.44100 0 0 0 0.6000 0.50000 0 0 0 0 0.5528ans =2.3587e-16L =1.0000 0 0 0 0 00.5000 0.8660 0 0 0 00.3333 0.5774 0.7454 0 0 00.2500 0.4330 0.5590 0.6614 0 00.2000 0.3464 0.4472 0.5292 0.6000 00.1667 0.2887 0.3727 0.4410 0.5000 0.5528ans =2.3682e-162)用对称正定矩阵求解线性系统
代码及运算
A = [1 0 1; 0 2 0; 1 0 3]
R = chol(A)%计算矩阵的 Cholesky 因子
b = sum(A,2);
x = R\(R'\b)A =1 0 10 2 01 0 3R =1.0000 0 1.00000 1.4142 00 0 1.4142x =1.00001.00001.00003、QR分解: qr QR 分解
语法
语法1:R = qr(A) 返回 QR 分解 A = Q*R 的上三角 R 因子。
语法2:[Q,R] = qr(A) 对 m×n 矩阵 A 执行 QR 分解,满足 A = Q*R。
语法3:[Q,R,P] = qr(A) 还返回一个置换矩阵 P,满足 A*P = Q*R。
1)Q-Less QR 分解
代码及运算
A = magic(5);%5*5幻方矩阵
R = qr(A)R =-32.4808 -26.6311 -21.3973 -23.7063 -25.86150.4648 19.8943 12.3234 1.9439 4.08560.0808 -0.0496 -24.3985 -11.6316 -3.74150.2021 -0.0460 0.3950 -20.0982 -9.97390.2223 -0.1755 0.4959 -0.8587 -16.00052)矩阵的完整 QR 分解
代码及运算
A = magic(5);
[Q,R] = qr(A)
norm(A-Q*R)Q =-0.5234 0.5058 0.6735 -0.1215 -0.0441-0.7081 -0.6966 -0.0177 0.0815 -0.0800-0.1231 0.1367 -0.3558 -0.6307 -0.6646-0.3079 0.1911 -0.4122 -0.4247 0.7200-0.3387 0.4514 -0.4996 0.6328 -0.1774R =-32.4808 -26.6311 -21.3973 -23.7063 -25.86150 19.8943 12.3234 1.9439 4.08560 0 -24.3985 -11.6316 -3.74150 0 0 -20.0982 -9.97390 0 0 0 -16.0005ans =9.6765e-15相关文章:

33、matlab矩阵分解汇总:LU矩阵分解、Cholesky分解和QR分解
1、LU矩阵分解 语法 语法1:[L,U] lu(A) 将满矩阵或稀疏矩阵 A 分解为一个上三角矩阵 U 和一个经过置换的下三角矩阵 L,使得 A L*U。 语法2:[L,U,P] lu(A) 还返回一个置换矩阵 P,并满足 A P*L*U。 语法3:[L,U,P] …...

C语言——使用函数创建动态内存
一、堆和栈的区别 1)栈(Stack): 栈是一种自动分配和释放内存的数据结构,存储函数的参数值、局部变量的值等。栈的特点是后进先出,即最后进入的数据最先出来,类似于我们堆盘子一样。栈的大小和生命周期是由系统自动管理的,不需要程序员手动释放。2)堆(Heap): 堆是由…...

【PL理论】(16) 形式化语义:语义树 | <Φ, S> ⇒ M | 形式化语义 | 为什么需要形式化语义 | 事实:部分编程语言的设计者并不会形式化语义
💭 写在前面:本章我们将继续探讨形式化语义,讲解语义树,然后我们将讨论“为什么需要形式化语义”,以及讲述一个比较有趣的事实(大部分编程语言设计者其实并不会形式化语义的定义)。 目录 0x00…...

前端杂谈-警惕仅引入一行代码言论
插入一行 JavaScript 代码似乎是一种无受害者犯罪。这只是一个小脚本,对吧?但 JavaScript 可以导入更多 JavaScript。-杰里米基思 “这只是一行代码”是我们经常听到的宣传语。这也可能是我们对自己和他人说的最大的谎言。 “仅用一行添加样式”&#x…...

有关cookie配置的一点记录
Domain:可以用在什么域名下,按最小化原则设Path:可以用在什么路径下,按最小化原则Max-Age和Expires:过期时间,只保留必要时间Http-Only:设置为true,这个浏览器上的JS代码将无法使用这…...

Oracle如何定位硬解析高的语句?
查询subpool 情况 select KSMDSIDX supool,round(sum(KSMSSLEN)/1024/1024,2) SQLA_size_mb from x$ksmss where KSMDSIDX<>0 and KSMSSNAMSQLA group by KSMDSIDX;查询subpool top5 SELECT *FROM (SELECT KSMDSIDX subpool,KSMSSNAM name,ROUND(KSMSSLEN / 102…...
Linux卸载残留MySQL【带图文命令巨详细】
Linux卸载残留MySQL 1、检查残留mysql2、检查并删除残留mysql依赖3、检查是否自带mariadb库 1、检查残留mysql 如果残留mysql组件,使用命令 rpm -e --nodeps 残留组件名 按顺序进行移除操作 #检查系统是否残留过mysql rpm -qa | grep mysql2、检查并删除残留mysql…...

4句话学习-k8s节点是如何注册到k8s集群并且kubelet拿到k8s证书的
一、kubelet拿着CSR(签名请求)使用的是Bootstrap token 二、ControllerManager有一个组件叫CSRAppprovingController,专门来Watch有没有人来使用我这个api. 三、看到有人拿着Bootstrap token的CSR来签名请求了,CSRAppprovingContr…...

2024全国大学生数学建模竞赛优秀参考资料分享
0、竞赛资料 优秀的资料必不可少,优秀论文是学习的关键,视频学习也非常重要,如有需要请点击下方名片获取。 一、赛事介绍 全国大学生数学建模竞赛(以下简称竞赛)是中国工业与应用数学学会主办的面向全国大学生的群众性科技活动,旨…...

QPS,平均时延和并发数
我们当前有两个服务A和B,想要知道哪个服务的性能更好,该用什么指标来衡量呢? 1. 单次请求时延 一种最简单的方法就是使用同一请求体同时请求两个服务,性能越好的服务时延越短,即 R T 返回结果的时刻 − 发送请求的…...
【Python核心数据结构探秘】:元组与字典的完美协奏曲
文章目录 🚀一、元组⭐1. 元组查询的相关方法❤️2. 坑点🎬3. 修改元组 🌈二、集合⭐1. 集合踩坑❤️2. 集合特点💥无序性💥唯一性 ☔3. 集合(交,并,补)🎬4. …...

Golang | Leetcode Golang题解之第137题只出现一次的数字II
题目: 题解: func singleNumber(nums []int) int {a, b : 0, 0for _, num : range nums {b (b ^ num) &^ aa (a ^ num) &^ b}return b }...

Spring和SpringBoot的特点
1.Spring的特点 1.IOC和AOP是Spring的两大核心特性,即控制反转和依赖注入。 2.松耦合:IOC和AOP两大特性可以尽可能地将对象之间的关系解耦 3.可配置:提供外部化配置的方式,可以灵活地配置容器及容器中的Bean 4.一站式:…...

怎么使用join将数组转为逗号分隔的字符串
在JavaScript中,你可以使用Array.prototype.join()方法将一个数组转换为逗号分隔的字符串。join()方法接受一个可选的参数,该参数指定了数组元素之间的分隔符。如果不提供参数,则默认使用逗号(,)作为分隔符。 下面是一…...

Web前端博客论坛:构建、运营与用户体验的深度解析
Web前端博客论坛:构建、运营与用户体验的深度解析 在数字化浪潮的推动下,Web前端博客论坛成为了广大开发者交流技术、分享经验的重要平台。如何构建一个功能齐全、运营有序的博客论坛,以及如何提升用户体验,是摆在每一位前端开发…...

Java从入门到放弃
线程池的主要作用 线程池的设计主要是为了管理线程,为了让用户不需要再关系线程的创建和销毁,只需要使用线程池中的线程即可。 同时线程池的出现也为性能的提升做出了很多贡献: 降低了资源的消耗:不会频繁的创建、销毁线程&…...
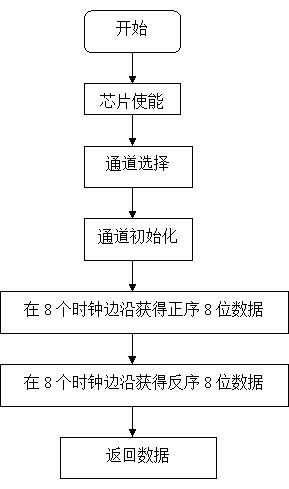
基于51单片机的车辆动态称重系统设计
一 动态称重 所谓动态称重是指通过分析和测量车胎运动中的力,来计算该运动车辆的总重量、轴重、轮重和部分重量数据的过程。动态称重系统按经过车辆行驶的速度划分,可分为低速动态称重系统与高速动态称重系统。因为我国高速公路的限速最高是120,所以高速动态称重系统在理论…...
C语言之常用字符串函数总结、使用和模拟实现
文章目录 目录 一、strlen 的使用和模拟实现 二、strcpy 的使用及模拟实现 三、strcat 的使用和模拟实现 四、strcmp 的使用和模拟实现 五、strncpy 的使用和模拟实现 六、strncat 的使用和模拟实现 七、strncmp 的使用和模拟实现 八、strstr 的使用和模拟实现 九、st…...
【JMeter接口测试工具】第二节.JMeter项目实战(上)【实战篇】
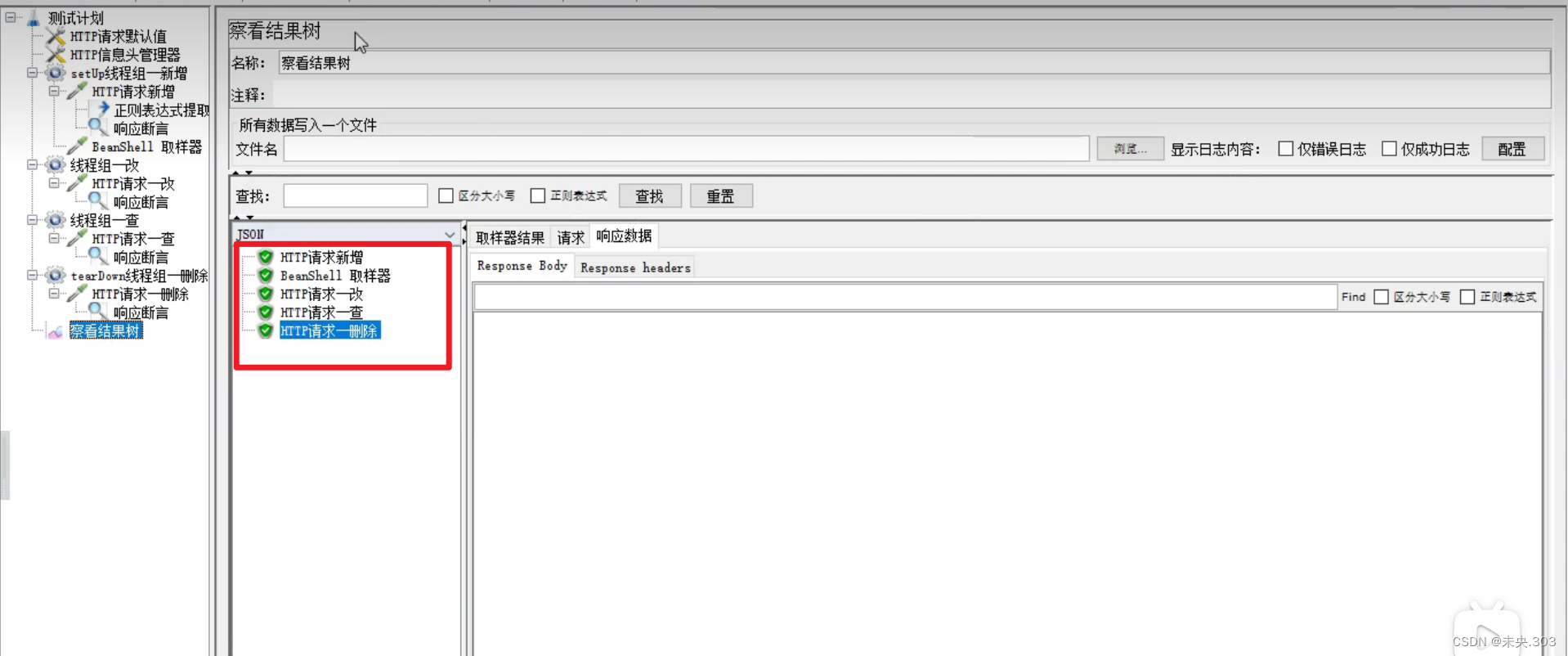
文章目录 前言项目实战零、接口测试流程一、测试数据准备二、接口功能测试三、掌握测试用例编写四、自动化脚本架构搭建总结 前言 零、接口测试流程 1、制定测试计划,分配任务 2、从 API 文档中提取接口清单:对 API 文档简化,提高测试效率,接口清单就是对 API 文档…...

Ansible——fetch模块
目录 参数 示例1:最基本的用法 示例2:指定目标目录和主机名子目录 示例3:flat 参数设置为 yes 示例4:处理源文件不存在的情况 示例5:验证文件校验和 示例 Playbook 1. 拉取远程主机上的 syslog 文件 2. 直接…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
