day28回溯算法part04| 93.复原IP地址 78.子集 90.子集II
**93.复原IP地址 **
本期本来是很有难度的,不过 大家做完 分割回文串 之后,本题就容易很多了
题目链接/文章讲解 | 视频讲解
class Solution {
public:vector<string> result;// pointNum记录加入的点的数量,其等于3的时候停止void backtracking(string& s, int startindex, int pointNum) {// 终止条件,逗号为3说明已经切割完了if (pointNum == 3) {// 只要分了三次,也就是有三个点之后// 直接判断最后一段,如果是的话就加入if (isvalid(s, startindex, s.size() - 1)) {result.push_back(s);}return;}for (int i = startindex; i < s.size(); i++) {// 判断[startindex, i]这个区间的子串是否合法if (isvalid(s, startindex, i)) {s.insert(s.begin() + i + 1, '.');pointNum++;backtracking(s, i + 2, pointNum);pointNum--;s.erase(s.begin() + i + 1);} else {// 不合法直接结束本层循环break;}}}bool isvalid(string& s, int start, int end) {// 1.段位以0开头的数字不合法// 2.段位里有非正整数字符不合法// 3.段位如果大于255不合法if (start > end)return false;// 0.0.0.0是合法的,start != end指的是01 0123这种情况if (s[start] == '0' && start != end) {return false;}int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;}vector<string> restoreIpAddresses(string s) {backtracking(s, 0, 0);return result;}
};
**78.子集 **
子集问题,就是收集树形结构中,每一个节点的结果。 整体代码其实和 回溯模板都是差不多的。
题目链接/文章讲解 | 视频讲解
class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums, int startindex) {result.push_back(path);// 确定结束条件if (startindex >= nums.size()) {return;}// 单层的处理逻辑for (int i = startindex; i < nums.size(); i++) {path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);return result;}
};
还是要熟悉这个回溯解题模板
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
**90.子集II **
大家之前做了 40.组合总和II 和 78.子集 ,本题就是这两道题目的结合,建议自己独立做一做,本题涉及的知识,之前都讲过,没有新内容。
题目链接/文章讲解 | 视频讲解
这题就是使用了之前的去重策略,在树层上进行去重,如果前一个数已经使用过了,就跳过一个树枝。
去重的时候要对数组进行排序,别忘记了
class Solution {
public:vector<int> path;vector<vector<int>> result;vector<bool> used;void backtracking(vector<int>& nums, int startindex) {result.push_back(path);if (startindex >= nums.size()) {return ;}for (int i = startindex; i < nums.size(); i++) {// 树层上去重,树层上进行跳过重复的if (i > 0 && nums[i - 1] == nums[i] && used[i - 1] == false) {continue;}used[i] = true;path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();used[i] = false;}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {// 初始化used = vector<bool>(nums.size(), false);// 去重需要排序sort(nums.begin(), nums.end());backtracking(nums, 0);return result;}
};
相关文章:

day28回溯算法part04| 93.复原IP地址 78.子集 90.子集II
**93.复原IP地址 ** 本期本来是很有难度的,不过 大家做完 分割回文串 之后,本题就容易很多了 题目链接/文章讲解 | 视频讲解 class Solution { public:vector<string> result;// pointNum记录加入的点的数量,其等于3的时候停止void b…...

SpringBoot项目启动时“jar中没有主清单属性”异常
资料参考 Spring Boot 启动时 “jar中没有主清单属性” 异常 - spring 中文网 (springdoc.cn) 实际解决 更详细的参考以上,我这边的话只需要在 pom文件 中加上 spring-boot-maven-plugin 插件就能解决该异常,具体如下: <build><p…...

vAttention:用于在没有Paged Attention的情况下Serving LLM
文章目录 0x0. 前言(太长不看版)0x1. 摘要0x2. 介绍&背景0x3. 使用PagedAttention模型的问题0x3.1 需要重写注意力kernel0x3.2 在服务框架中增加冗余0x3.3 性能开销0x3.3.1 GPU上的运行时开销0x3.3.2 CPU上的运行时开销 0x4. 对LLM服务系统的洞察0x5…...

Python实现Stack
你好,我是悦创。 Python 中的栈结构是一种后进先出(LIFO, Last In, First Out)的数据结构,这意味着最后添加到栈中的元素将是第一个被移除的。栈通常用于解决涉及到反转、历史记录和撤销操作等问题。在 Python 中,你可…...
分布式存储)
Helm在线部署Longhorn(1.6.0版本)分布式存储
环境依赖: k8s (版本大于等于v1.21版本)、helm工具 安装前准备 k8s worker 节点都需要执行 yum -y --setopttsflagsnoscripts install iscsi-initiator-utils echo "InitiatorName$(/sbin/iscsi-iname)" > /etc/iscsi/initiatorname.iscsi systemctl …...
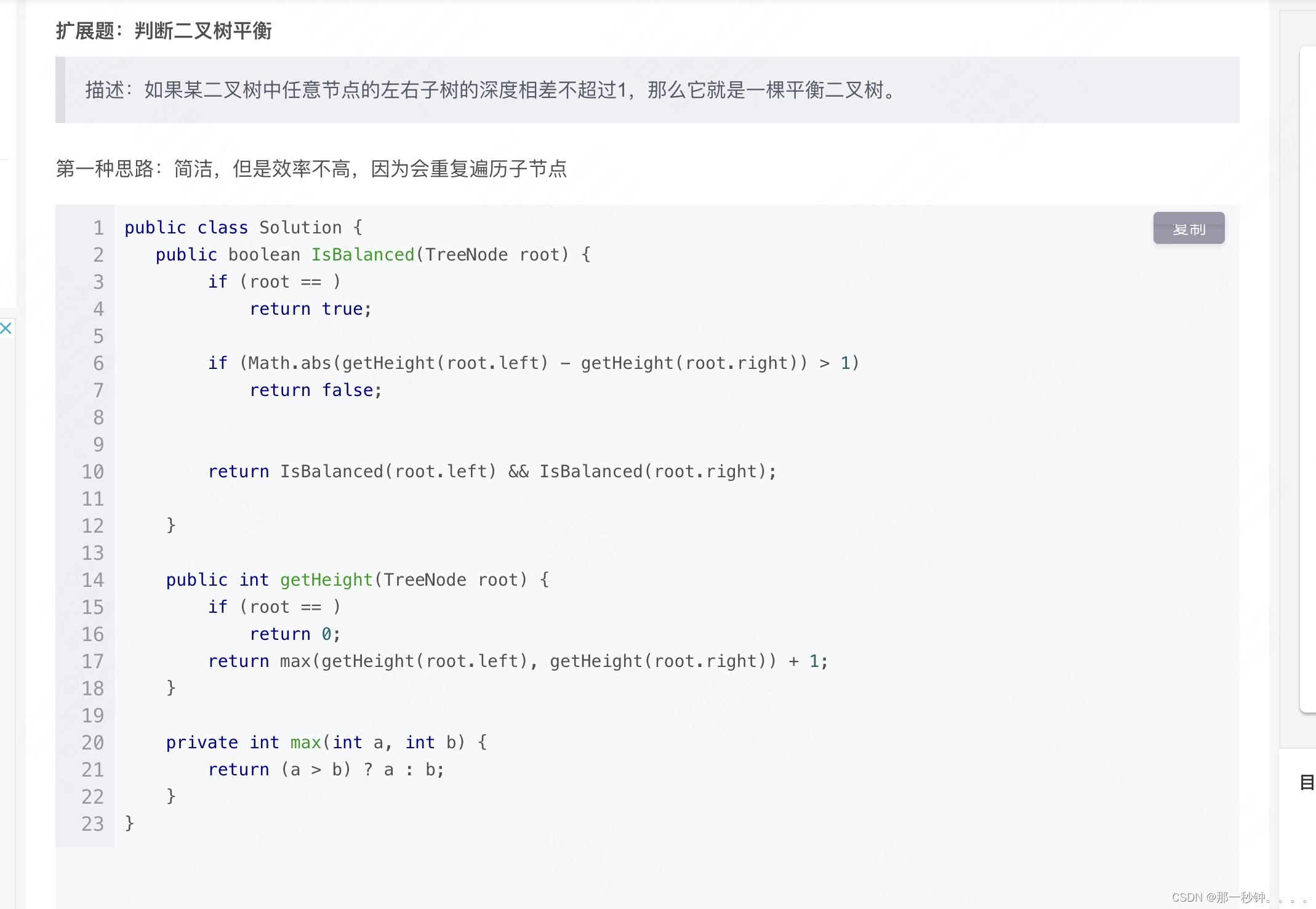
算法题目学习汇总
1、二叉树前中后序遍历:https://blog.csdn.net/cm15835106905/article/details/124699173 2、输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。 public class Solution {private Tr…...
DockerCompose中部署Jenkins(Docker Desktop在windows上数据卷映射)
场景 DockerJenkinsGiteeMaven项目配置jdk、maven、gitee等拉取代码并自动构建以及遇到的那些坑: DockerJenkinsGiteeMaven项目配置jdk、maven、gitee等拉取代码并自动构建以及遇到的那些坑_jenkins的安装以及集成jdkgitmaven 提示警告-CSDN博客 Windows10(家庭版…...

吊车报警的工作原理和使用场景_鼎跃安全
在现代建筑施工过程中,经常使用大型机械设备,如挖掘机、吊车、打桩机等,这些设备在施工过程中发挥着越来越重要的作用;同时,这些设备的作业频繁进行作业,对于接触到高压电线的风险也随之增加。大型机械设备…...

Spring5
文章目录 1. Spring 是什么?2. IoC3. Spring Demo4. IoC 创建对象的方式 / DI 方式注入的默认参数在哪里设定? 5. Spring 配置tx:annotation-driven 用于启用基于注解的事务管理 6. Bean的作用域7. 在Spring中有三种自动装配的方式1. 在xml中显式的配置2. 在java中…...

vue面试题二
一、请解释Vue中的双向数据绑定是什么? Vue中的双向数据绑定是一种机制,它使得数据的变化能够自动反映在用户界面上,同时用户界面中的输入也能够自动更新数据。这种机制实现了数据层(Model)和视图层(View&…...

软件设计师笔记-程序语言基础知识
编程语言之间的翻译形式 编程语言之间的翻译形式主要有三种:汇编、解释和编译。这三种方式在将源代码转换为机器可执行的代码时,有着各自的特点和流程。 汇编: 定义:汇编是低级语言(如汇编语言)到机器语言的一种翻译方式。汇编语言是为特定计算机或计算机系列设计的一种…...

在Windows上安装VMWare Pro 16.2(虚拟机)并从零安装CentOS 7.6镜像过程记录
本文详细记录了在Windows的VMWare Workstation Pro 16.2中安装CentOS 7.6 的过程,非常适合新手从零开始一步步安装。 文章目录 一、安装VMWare Workstation Pro 16.2并激活二、安装CentOS 7.62.1 下载CentOS7.6镜像文件2.2 创建新的虚拟机2.3 安装CentOS镜像一、安装VMWare Wo…...

NGINX之location和rewrite
一.NGINX常用的正则表达式 二.Location location作用:对访问的路径做访问控制或者代理转发 1.location 常用的匹配规则: 进行普通字符精确匹配,也就是完全匹配^~ / 表示普通字符匹配。使用前缀匹配。如果匹配成功,则不再匹配其它 …...
 -- merge函数)
Python数据框的合并(一) -- merge函数
目录 1 merge 函数详解 1.1 左连接(Left Join): 1.2 右连接(Right Join): 1.3 全连接(Full Join 或 Outer Join): 2 代码示例 2.1 加载模块并创建示例数据框 2.2 左连接 2.3 右连接 2.4 全连接 1 m…...
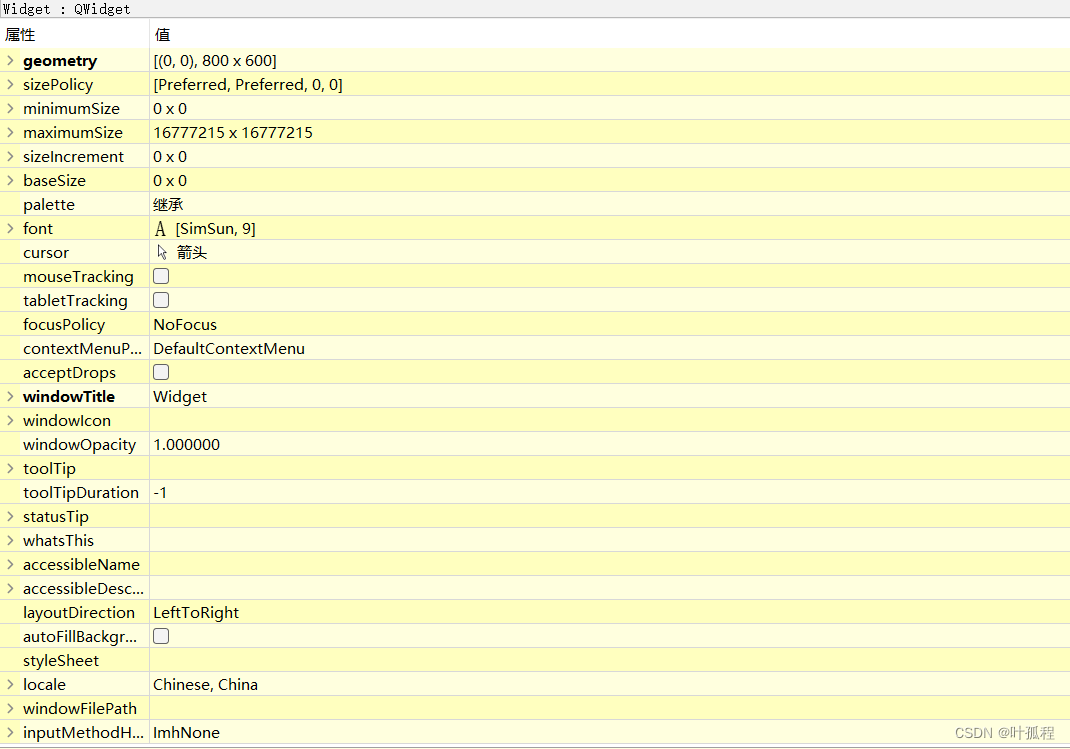
【Qt秘籍】[010]-Qt常用控件
一、控件概述 在GUI(图形用户界面)开发领域,Qt无疑是众多开发者心中的首选框架之一。它不仅跨平台、功能强大,而且拥有丰富且灵活的控件库,使得开发者能够快速构建美观、高效的用户界面。对于初学者而言࿰…...

TypeScript基础教程学习
菜鸟教程 TypeScript基础类型 数字类型 number 双精度 64 位浮点值。它可以用来表示整数和分数。 let binaryLiteral: number 0b1010; // 二进制 let octalLiteral: number 0o744; // 八进制 let decLiteral: number 6; // 十进制 let hexLiteral: number 0xf00d…...

JavaSE面试
①.简述面向对象的三大特征 封装、继承、多态 1.封装: 概念: 是将类的某些信息隐藏在类的内部,不允许外部程序直接访问,而是通过该类提供的方法来实现对隐藏信息的操作和访问。 好处 : ①便于修改,增强了代…...

安全漏洞扫描工具
常用的安全漏洞扫描工具涵盖了网络扫描、Web应用扫描、系统漏洞检测等多个方面,以下是一些业界广泛认可和常用的工具: Nmap - 网络映射和安全审计工具,用于发现网络上的主机和服务,识别操作系统,枚举开放端口ÿ…...
前端开发部署:Visual Studio Code + vue
〇 说明 本教程全部采用默认安装路径,因为在进行自定义路径安装的时候,需要配置各种环境变量,在这个配置过程中,可能出现各种很混乱的问题。 一 安装Node.js 1 下载https://nodejs.org/en 2 按照默认NEXT执行 C:\Program Files…...
基于Sentry+OpenTelemetry实现微服务前后端全链路监控
文章目录 前⾔背景技术⽅案Sentry私有化部署部署环境准备 项目集成前端后端agent探针集成sentry sdk集成增强探针为⽇志注⼊TraceID异常处理SDK⾃定义开发sentry sdk⾃定义开发⾃定义SentryEvent注⼊otel追踪信息⾃定义全局异常上报issue事件新增动态过滤功能 Java Agent Exten…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
