【数据结构】图论入门
引入
数据的逻辑结构:
- 集合:数据元素间除“同属于一个集合”外,无其他关系
- 线性结构:一个对一个,例如:线性表、栈、队列
- 树形结构:一个对多个,例如:树
- 图形结构:多个对多个,例如:图
图的基本概念及术语
图:G = ( V, E )
V:顶点(数据元素)的有穷非空集合
E:边的有穷集合
图的类型定义
无向图:每条边都是无方向的

有向图:每条弧都是有方向的

完全图:任意两个点都有一条边相连
- 无向完全图:n个结点就有n * (n - 1) / 2 条边
- 有向完全图:n个结点就有n * (n - 1) 条边
稀疏图:有很少的边或者弧的图(通常 m 远小于nlog(n))
稠密图:有较多的边或者弧的图(通常 m 大于nlog(n))
连通图:在无(有)向图G = (V,{E})中,若对任意两个顶点v、u,都存在v到u的路径,则称G是连通图(强连通图)
图的基本术语
-
网:边或者弧带权(有值)的图
-
邻接:有边 / 弧相连的两个顶点之间的关系
- 存在(Vi,Vj),则称 Vi 和 Vj 互为邻接点(无向图)
- 存在 <Vi,Vj>,则称 Vi 邻接到Vj,Vj 邻接于 Vi(有向图)
-
关联(依附):边 / 弧与顶点之间的关系
存在(Vi,Vj)/ <Vi,Vj>,则称该边/弧关联与Vi和Vj
-
顶点的度:与该顶点相关联的边的数目,记为TD(V)
在有向图当中,顶点的度等于该顶点的入度与出度之和
顶点V的入度是以V为终点的有向边的条数
以上图为例:
对于上面的有向图来说,每个结点的度都为2
对于上面的无向图来说,每个结点的度都为3,但是不同结点的入度、出度不一样(V3入度为1,出度为2)
-
路径:连接的边构成的顶点序列
-
路径长度:路径上边/弧的数目/权值之和
-
回路(环):第一个顶点和最后一个顶点相同的路径
-
简单路径:除路径起点和终点可以相同之外,其余顶点均不相同的路径
-
简单回路(简单环):除路径起点和终点相同之外,其余顶点均不相同的路径
-
子图:设有两个图G = (V,{E}),G1 = (V1,{E1}),若V1属于V并且E1属于E,则称G1是G的子图
-
连通分量(强连通分量):无(有)向图的极大连通子图称为G的连通分量(强连通分量)
- 极大连通子图:该子图是G连通子图,将G的任何不在该子图的顶点加入,此图不再连续
- 极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,此子图不再连续
图的存储结构
数组(邻接矩阵)表示法
概述
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间的关系)
-
设图A = (V,E)有n个顶点,则顶点表Vext[n]表示为
i 0 1 … n-1 Vext[i] V1 V2 … Vn -
图的邻接矩阵是一个二维数组A.arcs[n][n],定义为:
当存在<i,j>或者( i,j )属于图中的边或者弧,我们就将A.arcs[i][j]赋值为1,否则为0
举例
无向图

具体形况根据顶点的值去建立顶点表
邻接矩阵:
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| V1 | 0 | 1 | 0 | 1 | 0 |
| V2 | 1 | 0 | 1 | 0 | 1 |
| V3 | 0 | 1 | 0 | 1 | 1 |
| V4 | 1 | 0 | 1 | 0 | 0 |
| V5 | 0 | 1 | 1 | 0 | 0 |
特点:
- 无向图的邻接矩阵是对称的
- 顶点i的度 = 第i行(列)中1的个数
- 完全图的邻接矩阵中,对角元素为0,其余为1
代码演示见下面遍历部分
有向图

邻接矩阵:
| v1 | v2 | v3 | v4 | |
|---|---|---|---|---|
| v1 | 0 | 1 | 1 | 0 |
| v2 | 0 | 0 | 0 | 0 |
| v3 | 0 | 0 | 0 | 1 |
| v4 | 1 | 0 | 0 | 0 |
特点:
-
有向图的邻接矩阵可能是不对称的
-
顶点的出度 = 第i行元素之和
顶点的入度 = 第i列元素之和
顶点的度 = 出度 + 入度
网的邻接矩阵就是将1用权值替换
代码演示见下面遍历部分
优缺点
优点:
- 直观,简单,好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任意顶点的所有邻接点
- 方便计算出任意顶点的度
缺点:
- 不利于增加和删除顶点
- 浪费空间:存稀疏图,有大量无效元素
- 浪费时间:统计稀疏图中共有多少条边
邻接表
顶点:按编号顺序将顶点数据存储在一维数组中
关联同一顶点的边(以顶点为尾的弧):用线性链表存储
举例
仍以上图为例
无向图:

特点:
- 邻接表不唯一
- 若无向图中有n个顶点e条边,则其邻接表需n个头结点和2e个表结点,适宜存储稀疏图
- 无向图中顶点vi的度为第i个单链表中的结点数
代码演示见下面遍历部分
有向图:

特点:
- 顶点vi的出度为第i个单链表中的结点个数
- 顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数
代码演示见下面遍历部分
邻接矩阵与邻接表的关系:
1.联系:邻接表中每个链表对应于邻接矩阵中的每一行,链表中结点个数等于一行中非零元素的个数
2.区别:
a.对于任意确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(连接次序与顶点编号无关)
b.邻接矩阵的空间复杂度为O(n^2),而连接表的空间复杂度为O(n+e)
图的遍历
定义:从已给的连通图中某一顶点出发,沿着一些边访问图中所有的顶点,且每个顶点仅被访问一次,就叫做图的遍历,它是图的基本运算
实质:找每个顶点的邻接点的过程
问题:由图的特点,图中可能出现回路,且图的任一顶点都可能与其他结点相遇,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点,怎么避免重复访问?
解决思路:设置辅助数组a[n],用来标记每个被访问过的顶点,初始状态都为0,当顶点i被访问,改a[i]为1,防止被多次访问
深度优先搜索(DFS)
方法:
- 在访问图中某一起始顶点v后,由v出发,访问它的任一邻接顶点w1
- 再由w1出发访问与w1邻接,但还未被访问过的顶点w2
- 然后再从w2出发进行类似的访问…
- 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止
- 接着退回一步退到前一次刚访问过的顶点,看是否还有其他没有被访问的邻接顶点
- 如果有则访问此顶点,之后再从此顶点出发,进行与之前类似的访问
- 如果没有就再退回一步进行搜索,重复上述过程,直到连通图中所有顶点都被访问过为止
注意:
- 稠密图适于在邻接矩阵上进行深度遍历
- 稀疏图适于在连接表上进行深度遍历
对于邻接矩阵的代码演示:
public class GraphAdjacencyMatrix {private int V; // 顶点的数量private int[][] matrix; // 邻接矩阵private boolean[] visited;// 构造函数public GraphAdjacencyMatrix(int v) {V = v;matrix = new int[v][v];visited = new boolean[v];for (int i = 0; i < v; i++) {visited[i] = false;}}// 添加边public void addEdge(int v, int w, int weight) {matrix[v][w] = weight; // 因为是无向图,所以需要添加两个方向的边matrix[w][v] = weight;}//深度优先遍历private void DFS(int v) {visited[v] = true;System.out.print(v + " ");for (int i = 0; i < V; i++) {if (matrix[v][i] == 1 && !visited[i]) {DFS(i);}}}// 遍历所有顶点(如果顶点未访问,则进行DFS)public void DFSTraversal() {for (int i = 0; i < V; i++) {if (!visited[i]) {DFS(i); // 从顶点i开始DFS}}}// 打印图public void printGraph() {for (int i = 0; i < V; i++) {for (int j = 0; j < V; j++) {if (matrix[i][j] == 0) {System.out.print("0 ");} else {System.out.print(matrix[i][j] + " ");}}System.out.println();}}
}
public class linjiejuzhen {public static void main(String[] args) {GraphAdjacencyMatrix graph = new GraphAdjacencyMatrix(4);graph.addEdge(0, 1, 10); // 添加边 0-1 权重为 10graph.addEdge(0, 2, 6);graph.addEdge(1, 2, 4);graph.addEdge(2, 3, 1);System.out.println("Adjacency Matrix:");graph.printGraph();System.out.println("Depth First Traversal starting from vertex 0: ");graph.DFSTraversal(); //0 1 2 3}
}
Adjacency Matrix:
0 10 6 0
10 0 4 0
6 4 0 1
0 0 1 0
Depth First Traversal starting from vertex 0:
0 1 2 3
对于邻接表代码演示:
import java.util.Iterator;
import java.util.LinkedList;public class DirectedGraphAdjacencyList {private int V; // 顶点的数量private LinkedList<Integer> adj[];private boolean visited[]; // 邻接表// 构造函数public DirectedGraphAdjacencyList(int v) {V = v;adj = new LinkedList[v];visited = new boolean[v];for (int i = 0; i < v; i++) {adj[i] = new LinkedList<>();visited[i] = false;}}// 添加边public void addEdge(int v, int w) {adj[v].add(w); // 添加从顶点v到顶点w的有向边}// 打印图public void printGraph() {for (int i = 0; i < V; i++) {System.out.print("Vertex " + i + ":");Iterator<Integer> it = adj[i].iterator();while (it.hasNext()) {System.out.print(" -> " + it.next());}System.out.println();}}private void DFS(int v) {visited[v] = true;System.out.print(v + " ");Iterator<Integer> i = adj[v].listIterator();while (i.hasNext()) {int n = i.next();if (!visited[n]) {DFS(n); // 递归访问未访问的邻接顶点}}}// 遍历所有顶点执行DFSpublic void DFSTraversal() {for (int i = 0; i < V; i++) {if (!visited[i]) {DFS(i); // 从顶点i开始DFS}}}
}
public class DirectedGraphAdjacency {public static void main(String[] args) {DirectedGraphAdjacencyList graph = new DirectedGraphAdjacencyList(6);// 添加有向边graph.addEdge(5, 0);graph.addEdge(5, 3);graph.addEdge(4, 0);graph.addEdge(4, 1);graph.addEdge(2, 3);graph.addEdge(3, 1);graph.addEdge(1, 3);System.out.println("Adjacency List Representation of Directed Graph:");graph.printGraph();System.out.println("Depth First Traversal starting from vertex 0: ");graph.DFSTraversal(); //0 1 3 2 4 5}
}
Adjacency List Representation of Directed Graph:
Vertex 0:
Vertex 1: -> 3
Vertex 2: -> 3
Vertex 3: -> 1
Vertex 4: -> 0 -> 1
Vertex 5: -> 0 -> 3
Depth First Traversal starting from vertex 0:
0 1 3 2 4 5
广度优先搜索(BFS)
方法:
从图的某一结点出发,首先依次访问该结点的所有邻接结点 Vi1、Vi2……Vin,再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问的顶点。重复此过程,直至所有顶点均被访问为止
对于邻接矩阵的代码演示
import java.util.LinkedList;
import java.util.Queue;public class DirectedGraphAdjacencyMatrix {private int V; // 顶点的数量private int[][] matrix; // 邻接矩阵private boolean[] visited;// 构造函数public DirectedGraphAdjacencyMatrix(int v) {V = v;matrix = new int[v][v];visited = new boolean[v];// 初始化矩阵,所有元素都设置为0,表示没有边for (int i = 0; i < v; i++) {for (int j = 0; j < v; j++) {matrix[i][j] = 0;}visited[i] = false;}}// 添加边public void addEdge(int v, int w, int weight) {matrix[v][w] = weight; // 只在矩阵的对应位置添加边的权重}// 打印图public void printGraph() {for (int i = 0; i < V; i++) {for (int j = 0; j < V; j++) {if (matrix[i][j] == 0) {System.out.print(" 0 ");} else {System.out.print(" " + matrix[i][j] + " ");}}System.out.println();}}//广度优先搜索public void BFS(int start) {Queue<Integer> queue = new LinkedList<>();visited[start] = true; // 标记起始顶点为已访问queue.add(start); // 将起始顶点添加到队列中while (!queue.isEmpty()) {int v = queue.poll(); // 从队列中取出一个顶点System.out.print(v + " ");for (int i = 0; i < V; i++) {if (matrix[v][i] != 0 && !visited[i]) {visited[i] = true; // 标记邻接顶点为已访问queue.add(i); // 将邻接顶点添加到队列中}}}}
}
public class linjiejuzhenYou {public static void main(String[] args) {DirectedGraphAdjacencyMatrix graph = new DirectedGraphAdjacencyMatrix(4);graph.addEdge(0, 1, 10); // 添加有向边 0->1 权重为 10graph.addEdge(0, 2, 6);graph.addEdge(1, 2, 4);graph.addEdge(1, 3, 1);graph.addEdge(2, 3, 7);System.out.println("Directed Adjacency Matrix:");graph.printGraph();System.out.println("Breadth First Traversal starting from vertex 0: ");graph.BFS(0); //0 1 2 3}
}
Directed Adjacency Matrix:0 10 6 0 0 0 4 1 0 0 0 7 0 0 0 0
Breadth First Traversal starting from vertex 0:
0 1 2 3
对于邻接表的代码演示
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Queue;public class UndirectedGraphAdjacencyList {private int V; // 顶点的数量private LinkedList<Integer> adj[]; // 邻接表private boolean[] visited;// 构造函数public UndirectedGraphAdjacencyList(int v) {V = v;visited = new boolean[V];adj = new LinkedList[v];for (int i = 0; i < v; i++) {adj[i] = new LinkedList<>();visited[i] = false;}}// 添加边public void addEdge(int v, int w) {adj[v].add(w); // 添加从v到w的边adj[w].add(v); // 因为是无向图,所以需要添加从w到v的边}// 打印图public void printGraph() {for (int i = 0; i < V; i++) {System.out.print("Vertex " + i + ":");Iterator<Integer> it = adj[i].iterator();while (it.hasNext()) {System.out.print(" -> " + it.next());}System.out.println();}}public void BFS(int start) {Queue<Integer> queue = new LinkedList<>();visited[start] = true; // 标记起始顶点为已访问queue.add(start); // 将起始顶点添加到队列中while (!queue.isEmpty()) {int v = queue.poll(); // 从队列中取出一个顶点System.out.print(v + " ");Iterator<Integer> i = adj[v].listIterator();while (i.hasNext()) {int n = i.next();if (!visited[n]) {visited[n] = true; // 标记邻接顶点为已访问queue.add(n); // 将邻接顶点添加到队列中}}}}
}
public class UndirectedGraphAdjacency {public static void main(String[] args) {UndirectedGraphAdjacencyList graph = new UndirectedGraphAdjacencyList(4);graph.addEdge(0, 1); // 添加边 0-1graph.addEdge(0, 2);graph.addEdge(1, 2);graph.addEdge(2, 3);System.out.println("Adjacency List Representation of Undirected Graph:");graph.printGraph();System.out.println("Breadth First Traversal starting from vertex 0: ");graph.BFS(0); //0 1 2 3}
}
Adjacency List Representation of Undirected Graph:
Vertex 0: -> 1 -> 2
Vertex 1: -> 0 -> 2
Vertex 2: -> 0 -> 1 -> 3
Vertex 3: -> 2
Breadth First Traversal starting from vertex 0:
0 1 2 3
二者搜索的算法分析
时间复杂度:
邻接矩阵:
对于邻接矩阵表示的图,时间复杂度主要受两个因素影响:
-
矩阵大小:邻接矩阵的大小为 𝑉×𝑉,其中 V 是顶点的数量。
-
遍历矩阵:你需要遍历整个邻接矩阵来检查每个顶点的所有邻接点。
因此,对于邻接矩阵表示的图,时间复杂度为 𝑂(𝑉^2),这是因为你需要检查 V 个顶点,每个顶点可能与其他 V 个顶点相连。
邻接表:
对于邻接表表示的图,时间复杂度分析如下:
-
顶点数量:图有 V 个顶点。
-
边的数量:图有 E 条边。
-
访问邻接表:你访问每个顶点的邻接表,每个邻接表包含与该顶点直接相连的顶点。
-
队列操作:使用队列(栈)来存储待访问的顶点,每次从队列(栈)中取出一个顶点,并将其所有未访问的邻接顶点加入队列(栈)。
因此,对于邻接表表示的图,时间复杂度为 O(V+E)。这是因为你访问了所有 V 个顶点,并且每个顶点的邻接表(即所有边)也被访问了一次。
空间复杂度:空间复杂度相同,都是O(n)
相关文章:

【数据结构】图论入门
引入 数据的逻辑结构: 集合:数据元素间除“同属于一个集合”外,无其他关系线性结构:一个对一个,例如:线性表、栈、队列树形结构:一个对多个,例如:树图形结构࿱…...

11_1 Linux NFS服务与触发挂载autofs
11_1 Linux NFS服务与触发挂载服务 文章目录 11_1 Linux NFS服务与触发挂载服务[toc]1. NFS服务基础1.1 示例 2. 触发挂载autofs2.1 触发挂载基础2.2 触发挂载进阶autofs与NFS 文件共享服务:scp、FTP、web(httpd)、NFS 1. NFS服务基础 Netwo…...
开发uniapp 小程序时遇到的问题
1、【微信开发者工具报错】routeDone with a webviewId XXX that is not the current page 解决方案: 在app.json 中添加 “lazyCodeLoading”: “requiredComponents” uniapp的话加到manifest.json下的mp-weixin 外部链接文章:解决方案文章1 解决方案文章2 &qu…...
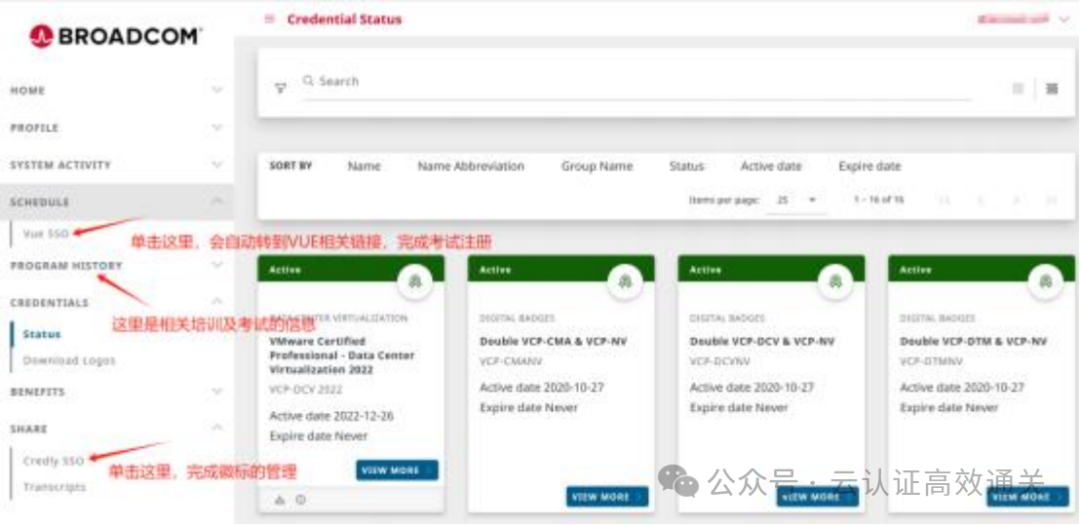
怎样快速获取Vmware VCP 证书,线上考试,voucher报名优惠
之前考一个VCP证书,要花大一万的费用,可贵了,考试费不贵,贵就贵在培训费,要拿到证书,必须交培训费,即使vmware你玩的很溜,不需要再培训了,但是一笔贵到肉疼的培训费你得拿…...

LeetCode 1141, 134, 142
目录 1141. 查询近30天活跃用户数题目链接表要求知识点思路代码 134. 加油站题目链接标签普通版思路代码 简化版思路代码 142. 环形链表 II题目链接标签思路代码 1141. 查询近30天活跃用户数 题目链接 1141. 查询近30天活跃用户数 表 表Activity的字段为user_id,…...

华为FPGA工程师面试题
FPGA工程师面试会涉及多个方面,包括基础知识、项目经验、编程能力、硬件调试和分析等。以下是一些必问的面试题: 基础知识题: 请解释FPGA的基本组成和工作原理。描述FPGA中的可编程互联资源以及它们在构建复杂数字电路中的作用。请解释嵌入式多用途块(如BRAM、DSP slices、…...
Windows11上安装docker(WSL2后端)和使用docker安装MySQL和达梦数据库
Windows11上安装docker(WSL2后端)和使用docker安装MySQL和达梦数据库 1. 操作系统环境2. 首先安装wsl2.1 关于wsl2.2 安装wsl2.3 查看可用的wsl2.4 安装ubuntu-22.042.5 查看、启动ubuntu-22.04应用2.6 上面安装开了daili2.7 wsl的更多参考 3. 下载Docke…...
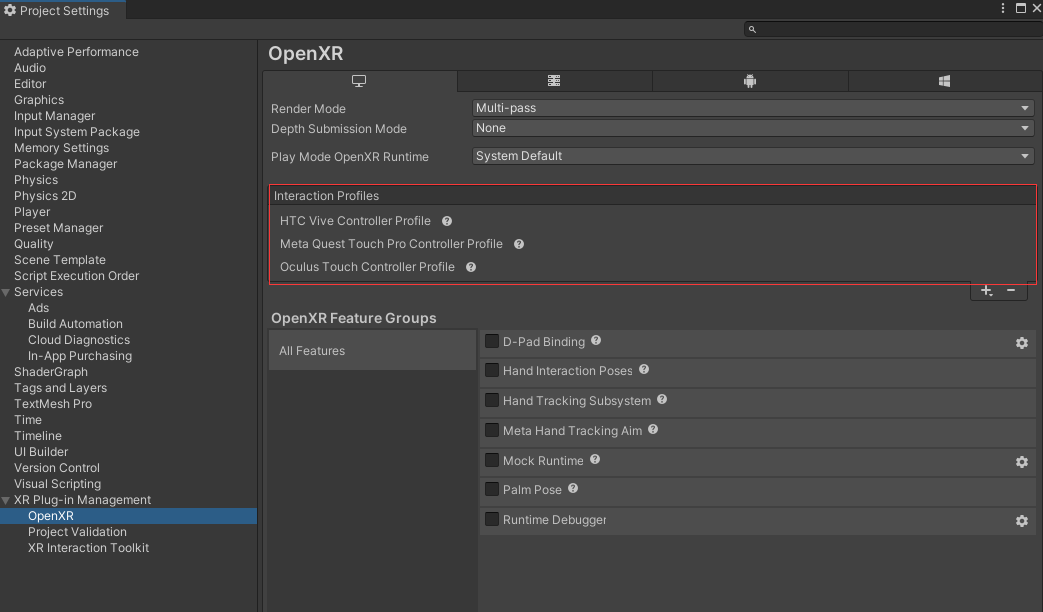
UnityXR Interactable Toolkit如何实现Climb爬梯子
前言 在VR中,通常会有一些交互需要我们做爬梯子,爬墙的操作,之前用VRTK3时,里面是还有这个Demo的,最近看XRI,发现也除了一个爬的示例,今天我们就来讲解一下 如何在Unity中使用XR Interaction Toolkit实现爬行(Climb)操作 环境配置 步骤 1:设置XR环境 确保你的Uni…...
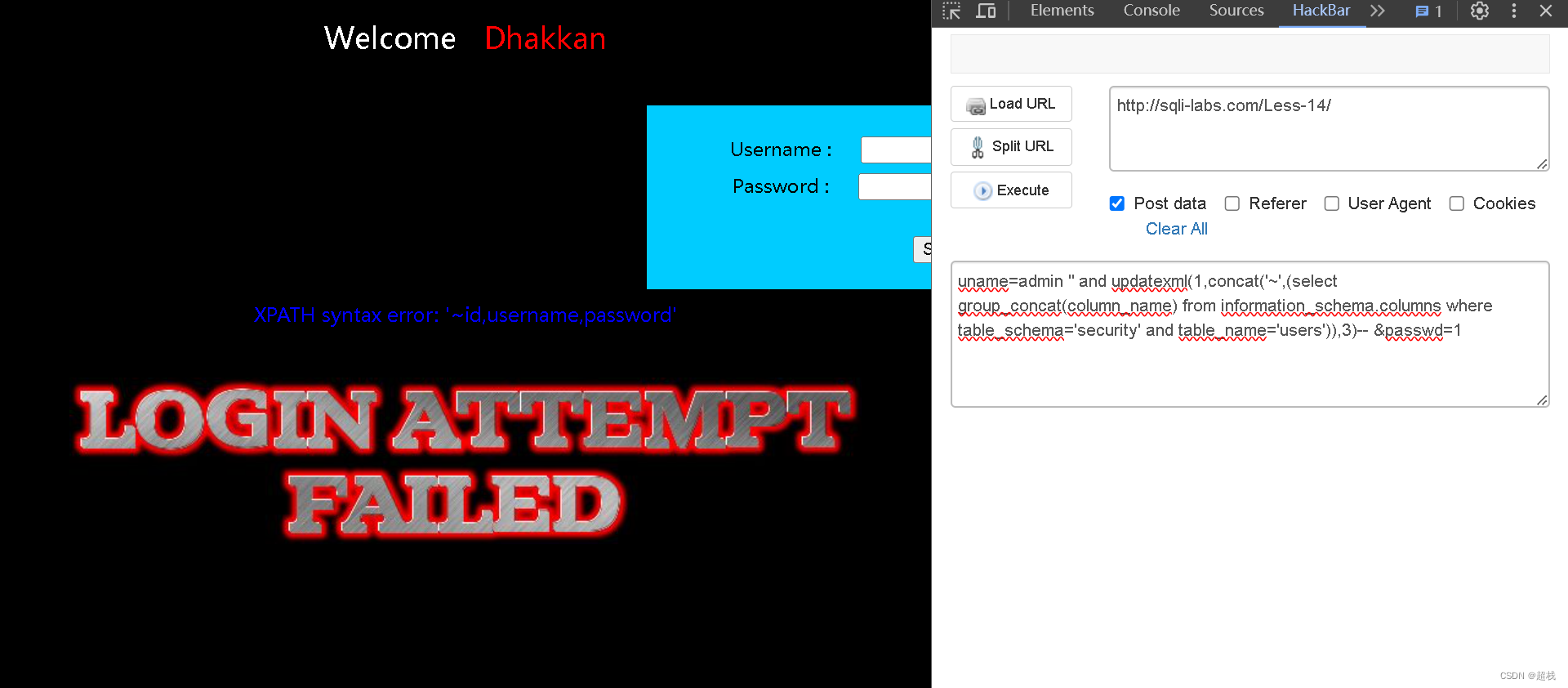
sqli-labs 靶场 less-11~14 第十一关、第十二关、第十三关、第十四关详解:联合注入、错误注入
SQLi-Labs是一个用于学习和练习SQL注入漏洞的开源应用程序。通过它,我们可以学习如何识别和利用不同类型的SQL注入漏洞,并了解如何修复和防范这些漏洞。Less 11 SQLI DUMB SERIES-11判断注入点 尝试在用户名这个字段实施注入,且试出SQL语句闭合方式为单…...

国内外网络安全现状分析
一、国内网络安全现状 1.1 国内网络安全威胁 国内的网络安全威胁主要表现在以下几个方面: 恶意软件:包括计算机病毒、蠕虫、木马和间谍软件等,它们能感染计算机系统、窃取敏感信息或破坏系统功能。网络钓鱼:通过伪装成可信任的…...

vscode copilot git commit 生成效果太差,用其他模型替换
问题 众所周知,copilot git commit 就像在随机生成 git commit 这种较为复杂的内容还是交给大模型做比较合适 方法 刚好,gitlens 最近开发了 AI commit的功能,其提供配置url api可以实现自定义模型 gitlens 只有3种模型可用:…...

计算机毕业设计hadoop+spark+hive舆情分析系统 微博数据分析可视化大屏 微博情感分析 微博爬虫 微博大数据 微博推荐系统 微博预测系统
本 科 毕 业 论 文 论文题目:基于Hadoop的热点舆情数据分析与可视化 姓名: 金泓羽 学号: 20200804050115 导师: 关英 职称&…...
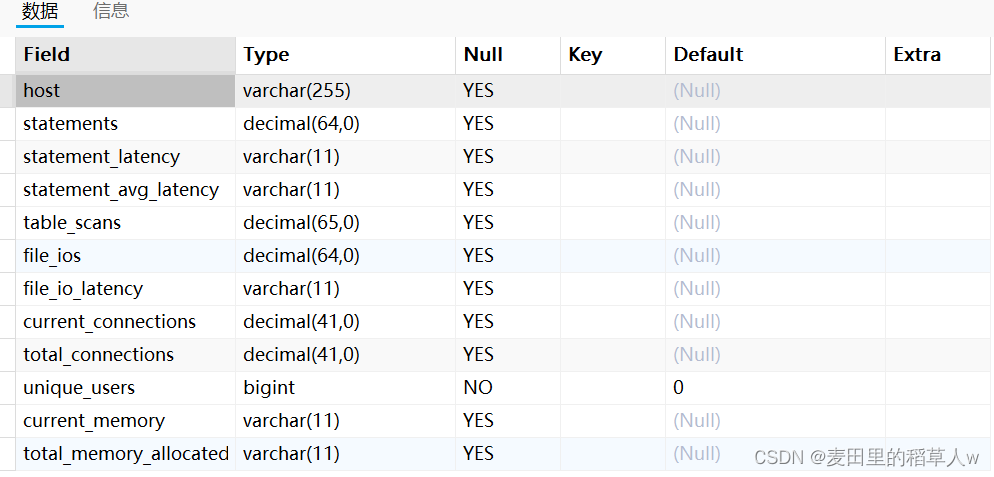
【MySQL】(基础篇二) —— MySQL初始用
MySQL初始用 目录 MySQL初始用基本语法约定选择数据库查看数据库和表其它的SHOW 在Navicat中,大部分数据库管理相关的操作都可以通过图形界面完成,这个很简单,大家可以自行探索。虽然Navicat等图形化数据库管理工具为操作和管理数据库提供了非…...
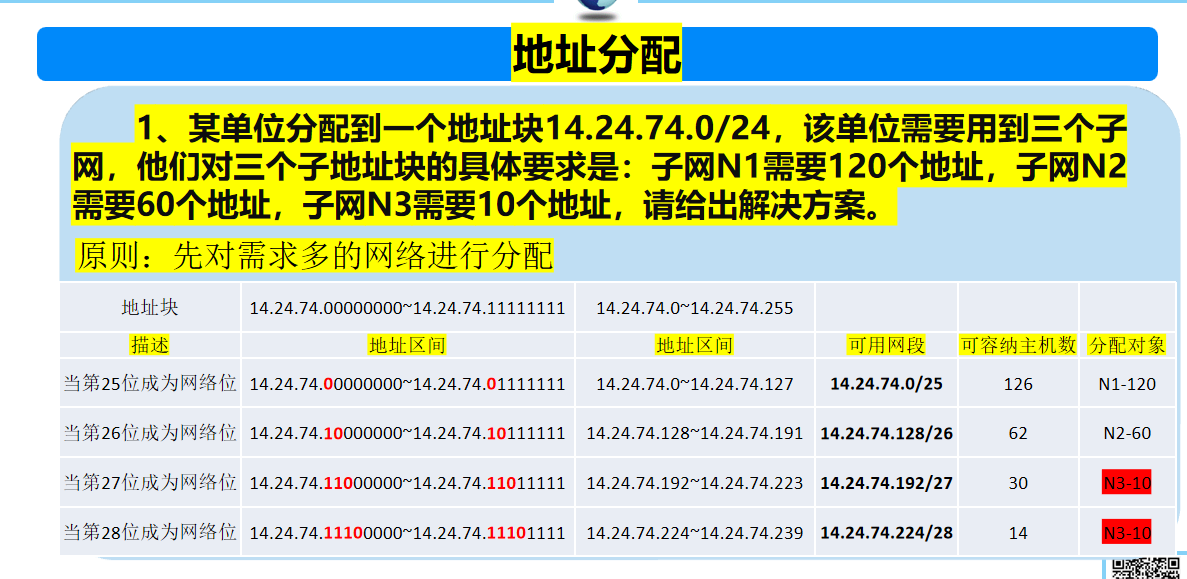
计算机网络 期末复习(谢希仁版本)第4章
路由器:查找转发表,转发分组。 IP网的意义:当互联网上的主机进行通信时,就好像在一个网络上通信一样,看不见互连的各具体的网络异构细节。如果在这种覆盖全球的 IP 网的上层使用 TCP 协议,那么就…...

如何使用Pandas处理数据?
一、技术难点 Pandas是Python中一个强大的数据处理和分析库,它提供了高效、灵活且易于使用的数据结构,主要用于数据清洗、转换、聚合和可视化等任务。然而,在使用Pandas处理数据时,也会遇到一些技术难点。 数据导入与导出&#…...

Error: spawn xdg-open ENOENT
报错:The CJS build of Vite’s Node API is deprecated. See https://vitejs.dev/guide/troubleshooting.html#vite-cjs-node-api-deprecated for more details. VITE v5.1.4 ready in 2298 ms ➜ Local: http://localhost:80/ ➜ Network: http://10.0.4.13:80/ ➜…...

写给大数据开发,如何去掌握数据分析
这篇文章源于自己一个大数据开发,天天要做分析的事情,发现数据分析实在高大上很多,写代码和做汇报可真比不了。。。。 文章目录 1. 引言2. 数据分析的重要性2.1 技能对比2.2 业务理解的差距 3. 提升数据分析能力的方向4. 数据分析的系统过程4…...

大数据湖一体化运营管理建设方案(49页PPT)
方案介绍: 本大数据湖一体化运营管理建设方案通过构建统一存储、高效处理、智能分析和安全管控的大数据湖平台,实现了企业数据的集中管理、快速处理和智能分析。该方案具有可扩展性、高性能、智能化、安全性和易用性等特点,能够为企业数字化…...
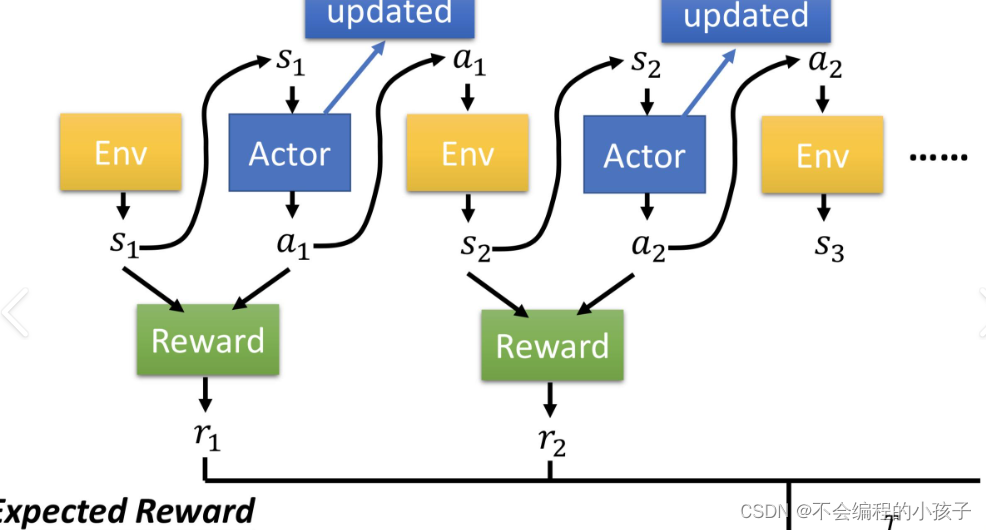
大模型训练的艺术:从预训练到增强学习的四阶段之旅
文章目录 大模型训练的艺术:从预训练到增强学习的四阶段之旅1. 预训练阶段(Pretraining)2. 监督微调阶段(Supervised Finetuning, SFT)3. 奖励模型训练阶段(Reward Modeling)4. 增强学习微调阶段…...
Linux 网络设置
Linux 网络设置 查看及测试网络查看网络配置测试网络连接 设置网络地址参数使用网络配置命令修改网络配置文件 查看及测试网络 查看及测试网络配置是管理 Linux 网络服务的第一步,本节将学习 Linux 操作系统中的网络查看及测试命令。其中讲解的大多数命令以普通用户权限就可以…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
