Dijkstra算法(迪杰斯特拉算法)
迪杰斯特拉算法通常用在图的最短路径问题上
而迷宫的最短路径可以用BFS来做,虽然BFS不能用于带权值的迷宫,但是可以对BFS稍微改进,只需要把判断是否走过的数组改为最短路径的数组,在判断是否可走时判断是否比最短的小即可
Dijkstra步骤如下:
1,初始化一个graph二维数组来存储图的邻接表,一个dis一维数组来存储最短路径,一个check来存储是否走过
2,从起点开始,将起点的路径设置为0,也就是disp[起点] = 0
3,进入循环,每次寻找dis中最小的节点,然后遍历邻接表,如果邻接表的距离+该点的dis < dis[循环到的点],那么就迭代循环到的点,最后将最小的那个点check设置为true
while(!end()){//寻找最小的点int min = max_num,min_num = max_num;for(int i = 1;i <= ::max;++i){if(dis[i] < min_num && !check[i]){min = i;min_num = dis[i];}}//从邻接表中寻找这个点可到达的点,并迭代可到达的点的距离for(int i = 1;i <= ::max;++i){if(graph[min][i] != max_num){if(dis[i] > dis[min] + graph[min][i]){dis[i] = dis[min] + graph[min][i];//经过最小的那个点到达这个点的距离为dis[min] + graph[min][i]}}}//将最小的那个点标记check[min] = true;}4,循环直到所有check都为true即可
也可以直接写一个函数判断
//这里写了一个函数判断是否都被标记
bool end()
{for(int i = 1;i <= ::max;++i){if(!check[i]){return false;}}return true;
}c++代码如下
#include <bits/stdc++.h>#define max_num 9999
using namespace std;int graph[max_num][max_num];//邻接表,存储图
int dis[max_num];//存储最短路径
bool check[max_num];//存储是否被标记
int max;//存储最大节点//这里写了一个函数判断是否都被标记
bool end()
{for(int i = 1;i <= ::max;++i){if(!check[i]){return false;}}return true;
}void dijkstra(int e)
{while(!end()){//寻找最小的点int min = max_num,min_num = max_num;for(int i = 1;i <= ::max;++i){if(dis[i] < min_num && !check[i]){min = i;min_num = dis[i];}}//从邻接表中寻找这个点可到达的点,并迭代可到达的点的距离for(int i = 1;i <= ::max;++i){if(graph[min][i] != max_num){if(dis[i] > dis[min] + graph[min][i]){dis[i] = dis[min] + graph[min][i];//经过最小的那个点到达这个点的距离为dis[min] + graph[min][i]}}}//将最小的那个点标记check[min] = true;}
}int main()
{//初始化,memset不可以用INT_MAX赋值,因为INT_MAX为无符号数最大值为1111111111111111,而memset会将其转换为有符号数的补码也就是-1memset(dis,max_num,sizeof(dis));memset(check, false,sizeof(check));memset(graph,max_num,sizeof(graph));int n;cin >> n >> ::max;int times = n;while(times--){int x,y,z;cin >> x >> y >> z;graph[x][y] = z;graph[y][x] = z;}#if 0//输出邻接表for(int i = 0;i <= ::max;++i){for(int j = 0;j <= ::max;++j){printf("%5d ",graph[i][j]);}cout << endl;}
#endif//起点启动int start;cin >> start;dis[start] = 0;dijkstra(start);//输出每个点到起点的最短路径for(int i = 1;i <= ::max;++i){cout << i << " : " << dis[i] << endl;}
}
/*
10 7
1 3 2
1 2 5
2 4 9
3 4 3
3 6 2
4 6 4
4 5 8
5 6 9
5 7 3
6 2 7
1
*/相关文章:
)
Dijkstra算法(迪杰斯特拉算法)
迪杰斯特拉算法通常用在图的最短路径问题上 而迷宫的最短路径可以用BFS来做,虽然BFS不能用于带权值的迷宫,但是可以对BFS稍微改进,只需要把判断是否走过的数组改为最短路径的数组,在判断是否可走时判断是否比最短的小即可 Dijks…...
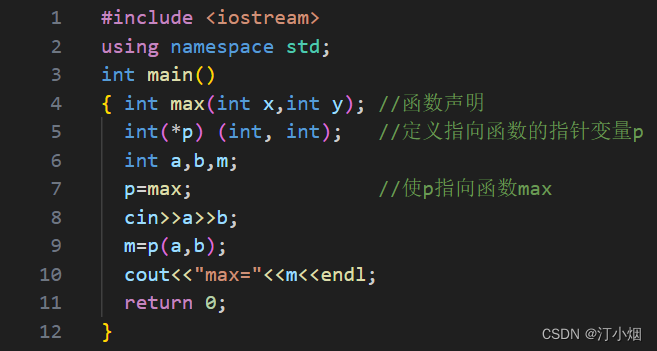
用函数指针求a和b中的大者
指针变量也可以指向一个函数。一个函数在编译时被分配给一个入口地址。这个函数入口地址就称为函数的指针。可以用一个指针变量指向函数,然后通过该指针变量调用此函数。 先按一般方法编写程序: 可以用一个指针变量指向max函数,然后通过该指…...

鸿蒙轻内核M核源码分析系列六 任务及任务调度(2)任务模块
任务是操作系统一个重要的概念,是竞争系统资源的最小运行单元。任务可以使用或等待CPU、使用内存空间等系统资源,并独立于其它任务运行。鸿蒙轻内核的任务模块可以给用户提供多个任务,实现任务间的切换,帮助用户管理业务程序流程。…...

解决找不到MSVCR120.dll,无法执行代码
msvcr120.dll是Microsoft Visual C 2013 Redistributable Package的一部分,它提供了运行使用Microsoft Visual C 2013编译器编译的程序所需的运行时环境。这个DLL文件包含了在运行使用Visual C编译器(特别是2013版)编译的应用程序时所必需的一…...
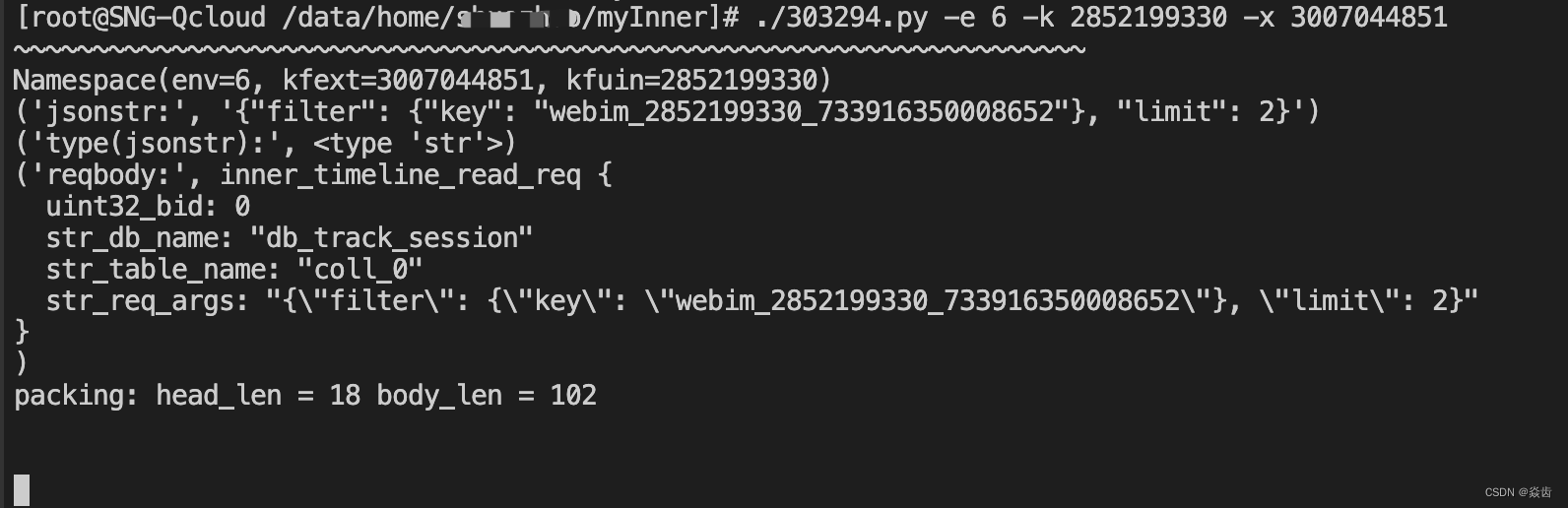
Linux iptables详解
前言:事情是这样的。最近部门在进行故障演练,攻方同学利用iptables制造了一个故障。演练最终肯定是取得了理想的效果,即业务同学在规定时间内定位了问题并恢复了业务(ps:你懂得)。 对我个人来讲一直知道iptables的存在࿰…...

Mac电脑arm64芯片Cocoapods 的 ffi 兼容问题
转载请标明出处:https://blog.csdn.net/donkor_/article/details/139505395 文章目录 前言问题分析解决方案总结 前言 今天在改Flutter项目的时候,构建IOS项目时,Cocoapods报错 Error: To set up CocoaPods for ARM macOS, run: arch -x86_6…...
如何提高逻辑性?(小妙招)
在现代社会中,逻辑性是一种至关重要的思维能力。不论是在工作、学习还是生活中,逻辑清晰的人总能更好地解决问题和做出决策。然而,如何提高逻辑性却是许多人头疼的问题。本文将从六个方面详细探讨如何提升逻辑性,包括细心态度、逼…...
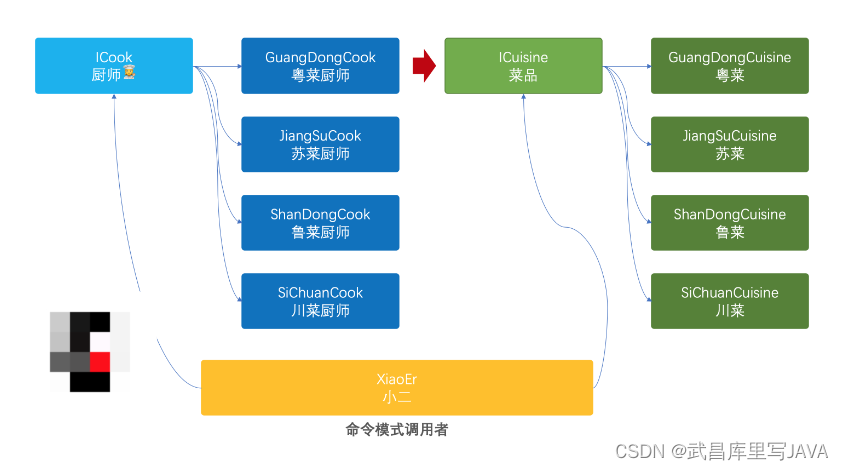
2024050501-重学 Java 设计模式《实战命令模式》
重学 Java 设计模式:实战命令模式「模拟高档餐厅八大菜系,小二点单厨师烹饪场景」 一、前言 持之以恒的重要性 初学编程往往都很懵,几乎在学习的过程中会遇到各种各样的问题,哪怕别人那运行好好的代码,但你照着写完…...

0104__Linux 中 nm 命令简介
Linux 中 nm 命令简介_linux nm-CSDN博客...

Linux网络服务
01 Linux网络设置 02 DHCP原理与配置 03 DNS域名解析服务 04 远程访问及控制 05 部署YUM仓库及NFS共享服务 06 PXE高效批量网络装机...

Vue18-列表渲染
一、v-for渲染列表 1-1、遍历数组(用的多) 1-2、key属性 让每一个<li>都有一个唯一的标识! 1、写法一 只有用了遍历的方式(v-for)来生成多个同样结构的数据,必须给每个结构取一个唯一的标识。 2、写法二 或者:…...

【三维重建】增量SFM系统
在学习完鲁鹏老师的三维重建基础后,打算用C代码复现一下增量SFM系统(https://github.com/ldx-star/SFM)。 本项目的最终目标就是通过相机拍摄的多视角视图获取三维点云。由于资金有效,博主使用的是相机是小米12。 先来看一下最终…...
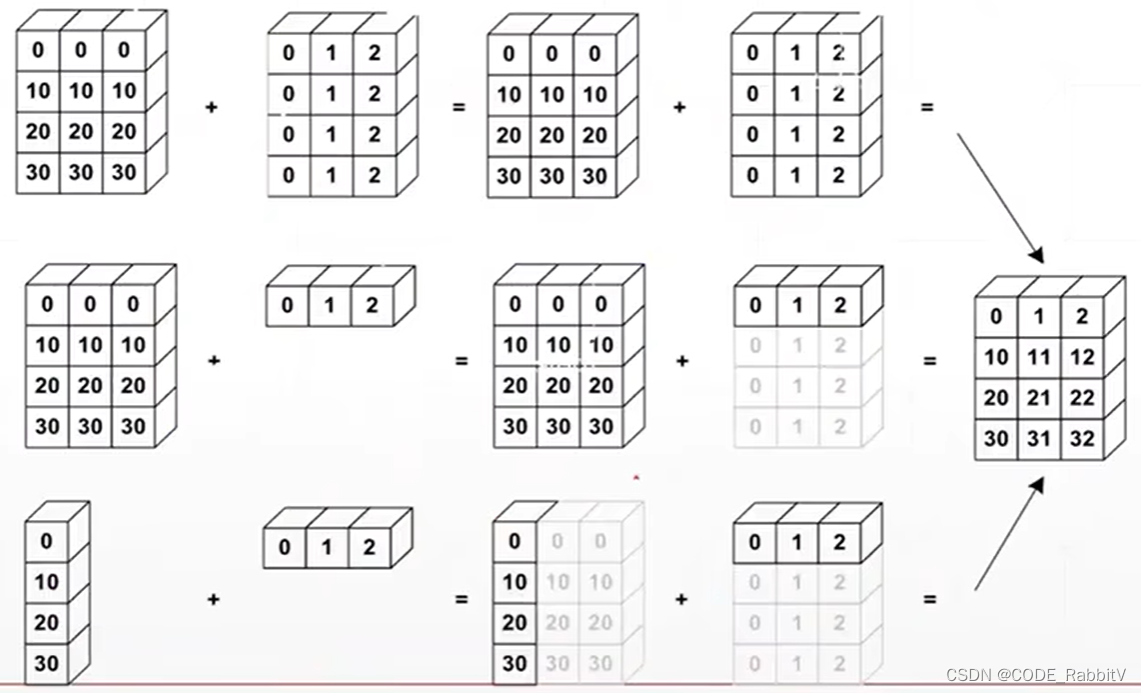
PyTorch 维度变换-Tensor基本操作
以如下 tensor a 为例,展示常用的维度变换操作 >>> a torch.rand(4,3,28,28) >>> a.shape torch.Size([4, 3, 28, 28])view / reshape 两者功能完全相同: a.view(shape) >>> a.view(4,3,28*28) ## a.view(4,3,28,28) 可恢复squeeze…...

spring 事务失效的几种场景
一、背景 在 springBoot 开发过程中,我们一般都是在业务方法上添加 Transactional 注解来让 spring 替我们管理事务,但在某些特定的场景下,添加完注解之后,事务是不生效的,接下来详细介绍下。 二、方法不是 public 2…...
45岁程序员独白:中年打工人出路在哪里?
作为一名也是JAVA方向的互联网从业者,我发现周围超过40岁以上的同事,基本都是部门负责人或者高层,真正还在一线做开发或者当个小领导的,已经是凤毛麟角了。 同事A今年刚满40,育有一儿一女,从进入公司到现在…...

深度探讨:为何训练精度不高却在测试中表现优异?
深度探讨:为何训练精度不高却在测试中表现优异? 在深度学习领域,我们经常遇到这样一个看似矛盾的现象:模型在训练集上的精度不是特别高,但在测试集上却能达到出色的表现。这种情况虽然不是常规,但其背后的…...

动态内存管理<C语言>
导言 在C语言学习阶段,指针、结构体和动态内存管理,是后期学习数据结构的最重要的三大知识模块,也是C语言比较难的知识模块,但是“天下无难事”,只要认真踏实的学习,也能解决,所以下文将介绍动态…...

第一百零二节 Java面向对象设计 - Java静态内部类
Java面向对象设计 - Java静态内部类 静态成员类不是内部类 在另一个类的主体中定义的成员类可以声明为静态。 例子 以下代码声明了顶级类A和静态成员类B: class A {// Static member classpublic static class B {// Body for class B goes here} }注意 静态成…...

给自己Linux搞个『回收站』,防止文件误删除
linux没有像windows里一样的回收站,工作时候删除文件容易不小心删错,造成麻烦的后果。所以给自己整了个回收站: 文件删除,新建~/opts/move_to_trash.sh,然后在里面新增,将${your_name}改成你的用户名。同时…...

Springboot接收参数的21种方式
前言 最近一直在忙着开发项目(ps:其实有些摆烂),好久没有更新博客了,打开csdn一看好多网友留言私信,继上篇博客(我是如何实现HttpGet请求传body参数的!),网友议论纷纷,各抒起见。今天正好抽出时间总结一下Springboot接受参数的21种方式(Post、Get、Delete),一并…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
