基于蚁群算法的二维路径规划算法(matlab)
微♥关注“电击小子程高兴的MATLAB小屋”获得资料
一、理论基础
1、路径规划算法
路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径。路径规划算法较多,大体上可分为全局路径规划算法和局部路径规划算法两大类。其中,全局路径规划算法包括位形空间法、广义锥方法、顶点图像法、栅格划归法;局部路径规划算法主要有人工势场法等。
2、MAKLINK图论理论
MAKLINK图论可以建立二维路径规划的空间模型,其通过生成大量的MAKLINK线构造二维路径规划可行空间。MAKLINK线定义为两个障碍物之间不与障碍物相交的顶点之间的连线,以及障碍物顶点与边界相交的连线。典型MAKLINK图形如图1所示。
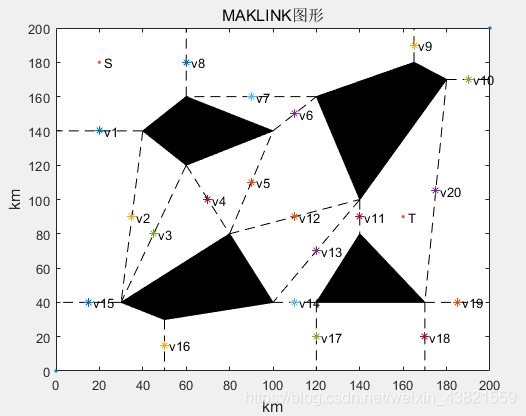
图1 MAKLINK图形
在MAKLINK图上存在I条自由连接线,连接线的中点依次为1,V2,连接所有MAKLINK线的中点加上始点S和终点工构成用于初始路径规划的无向网络图,如图2所示。
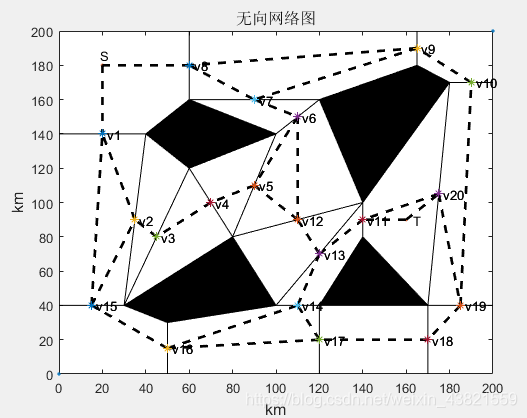
图2 无向网络图
3、蚁群算法
请参考这里
4、dijkstra算法
dijkstra算法是典型的单源最短路径算法,用于计算非负权值图中一个节点到其他所有节点的最短路径,其基本思想是把带权图中所有节点分为两组,第1组包括已确定最短路径的节点,第2组为未确定最短路径的节点。按最短路径长度递增的顺序逐个把第2组的节点加入第1组中,直到从源点出发可达的所有节点都包含在第1组中。
dijkstra算法流程如下:
(1)初始化存放未确定最短路径的节点集合V VV和已确定最短路径的节点集合S SS,利用带权图的邻接矩阵arcs初始化源点到其他节点最短路径长度D DD,如果源点到其他节点有连接弧,对应的值为连接弧的权值,否则对应的值取为极大值。
(2)选择D DD中的最小值D DD[i ii],D DD[i ii]是源点到点i ii的最短路径长度,把点i ii从集合V VV中取出并放入集合S SS中。
(3)根据节点i ii修改更新数组D DD中源点到集合V VV中所有节点k kk对应的路径长度值。
(4)重复步骤(2)和步骤(3)的操作,直至找出源点到所有节点的最短路径为止。
二、案例背景
1、问题描述
采用蚁群算法在200×200的二维空间中寻找一条从起点S SS到终点T TT的最优路径,该二维空间中存在4个障碍物,障碍物1的4个顶点的坐标分别为(40 140;60 160;100 140;60 120),障碍物2的4个顶点分别为(50 30;30 40;80 80;100 40),障碍物3的4个顶点分别为(120 160;140 100;180 170;165 180),障碍物4的3个顶点分别为(120 40;170 40;140 80),其中点S SS为起点,起点坐标为(20,180);点T TT为终点,终点坐标为(160,90)。二维规划空间如图3所示。
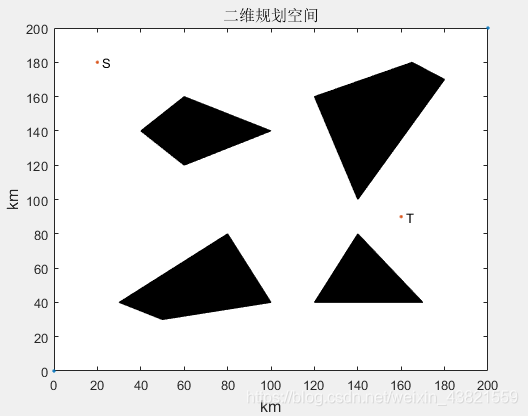
2、算法流程
算法流程如图4所示。其中,空间模型建立采用MAKLINK图论算法建立路径规划的二维空间,初始路径规划利用dijkstra算法规划出一条从起点到终点的初始路径,初始化算法参数,信息素更新采用根据蚂蚁搜索到的路径的长短优劣更新节点的信息素。
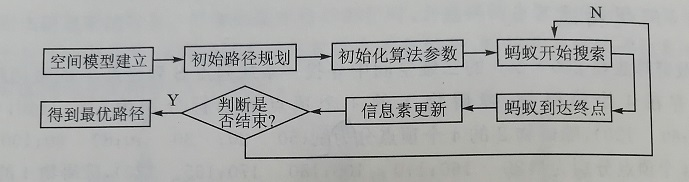
三、MATLAB程序
根据蚁群算法原理,在MATLAB软件中编程实现基于蚁群算法的二维路径规划算法,算法分为两步:第一步使用dijkstra算法生成初始次优路径;第二步在初始路径的基础上,使用蚁群算法生成全局最优路径。
1、dijkstra算法
采用dijkstra算法规划初始路径,其算法思想是先计算点点之间的距离,然后依次计算各点到出发点的最短距离,程序如下:
function path = DijkstraPlan(position,sign) %% 基于Dijkstra算法的路径规划算法 % position input 节点位置 % sign input 节点间是否可达 % path output 规划路径 %% 计算路径距离 cost = ones(size(sign))*10000; [n, m] = size(sign); for i = 1:nfor j = 1:mif sign(i, j) == 1cost(i, j) = sqrt(sum((position(i, :)-position(j, :)).^2));endend end%% 路径开始点 dist = cost(1, :); % 节点间路径长度 s = zeros(size(dist)); % 节点经过标志 s(1) = 1; dist(1) = 0; path = zeros(size(dist)); % 依次经过的节点 path(1, :) = 1;%% 循环寻找路径点 for num = 2:n% 选择路径长度最小点mindist = 10000;for i = 1:length(dist)if s(i) == 0if dist(i)< mindistmindist = dist(i);u = i;endendend% 更新点点间路径s(u) = 1;for w = 1:length(dist)if s(i) == 0if dist(u)+cost(u,w) < dist(w)dist(w) = dist(u)+cost(u,w);path(w) = u;endendend end
2、蚁群算法搜索
在初始路径的基础上,采用蚁群算法搜索最优路径,程序如下:
%% 蚁群算法参数初始化 pathCount = length(path)-2; % 经过线段数量 pheCacuPara = 2; % 启发值重要程度因子 pheThres = 0.8; % 信息素选择阈值 pheUpPara = [0.1 0.0003]; % 信息素更新参数 qfz = zeros(pathCount, 10); % 启发值 phePara = ones(pathCount, 10)*pheUpPara(2); % 信息素 qfzPara1 = ones(10,1)*0.5; % 启发信息参数1 qfzPara2 = 1.1; % 启发信息参数2 m=10; % 蚂蚁数量 NC=500; % 循环次数 pathk = zeros(pathCount, m); % 搜索结果记录 shortestpath = zeros(1,NC); % 进化过程记录 shortestroute = zeros(NC, 2*pathCount); % 每一代的最短路径 %% 初始最短路径 dijpathlen = 0; vv = zeros(22, 2); vv(1, :) = S; vv(22, :) = T; vv(2:21, :) = v; for i=1:pathCount-1dijpathlen = dijpathlen +sqrt(sum((vv(path(i), :)-vv(path(i+1), :)).^2)); % dijpathlen = dijpathlen + sqrt((vv(path(i),1)-vv(path(i+1),1))^2+(vv(path(i),2)-vv(path(i+1),2))^2); end LL = dijpathlen;%% 经过的链接线 lines = zeros(pathCount, 4); for i = 1:pathCountlines(i, 1:2) = B(L(path(i+1)-1, 1), :);lines(i, 3:4) = B(L(path(i+1)-1, 2), :); end%% 循环搜索 for num = 1:NC %% 蚂蚁迭代寻优一次for i = 1:pathCountfor k = 1:mq = rand();qfz(i, :) = (qfzPara2-abs((1:10)'/10-qfzPara1))/qfzPara2; % 启发信息if q <= pheThres % 选择信息素最大值arg = phePara(i, :).*(qfz(i, :).^pheCacuPara);j = find(arg == max(arg));pathk(i, k) = j(1);else % 轮盘赌选择arg = phePara(i, :).*(qfz(i, :).^pheCacuPara);sumarg = sum(arg);qq = (q-pheThres)/(1-pheThres);qtemp = 0;j = 1;while qtemp < qqqtemp = qtemp + (phePara(i, j)*(qfz(i, j)^pheCacuPara))/sumarg;j = j+1;endj = j-1;pathk(i, k) = j(1);end% 实时信息素更新phePara(i, j) = (1-pheUpPara(1))*phePara(i, j)+pheUpPara(1)*pheUpPara(2);endend%% 计算路径长度len = zeros(1, k);for k = 1:mPstart = S;Pend = lines(1, 1:2) + (lines(1, 3:4)-lines(1, 1:2))*pathk(1, k)/10;for l = 1:pathCountlen(1, k) = len(1, k)+sqrt(sum((Pend-Pstart).^2));Pstart = Pend;ant_route(k, 2*l-1:2*l)=Pstart;if l < pathCountPend = lines(l+1, 1:2) + (lines(l+1, 3:4)-lines(l+1, 1:2))*pathk(l+1, k)/10;endendPend = T;len(1, k) = len(1, k)+sqrt(sum((Pend-Pstart).^2));end%% 更新信息素% 寻找最短路径minlen = min(len);minant = find(len == minlen);minant = minant(1);shortestroute(num, :) = ant_route(minant, :);% 更新全局最短路径if minlen < LLLL = minlen;LL_route = shortestroute(num, :);end% 路径信息素更新for i = 1:pathCountphePara(i, pathk(i, minant)) = (1-pheUpPara(1))* phePara(i, pathk(i, minant))+pheUpPara(1)*(1/minlen);endshortestpath(num) = LL; end
3、结果分析
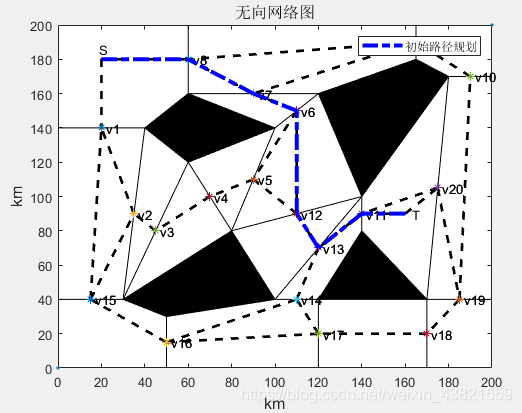
在无向网络图的基础上采用dijkstra算法规划初始路径,初始路径规划结果如图5所示。
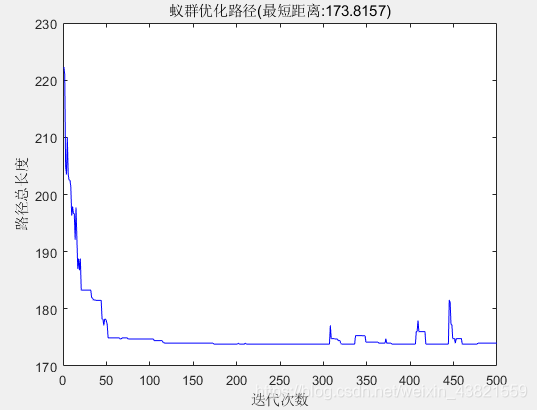
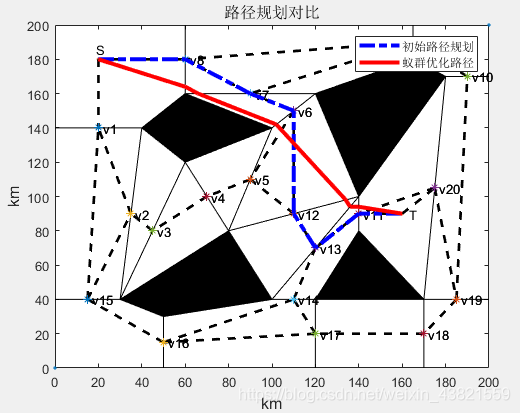
在初始路径规划的基础上采用蚁群算法进行详细路径规划。根据初始路径规划结果判断路径经过的链路为v8→v7→v6→v12→v13→v11,每条链路均离散化为10个小路段,蚂蚁个数为10,个体长度为6,算法进化次数共500次,迭代过程中路径总长度变化及规划出的路径如图6和图7所示。
Command Window中结果显示为:
初始路径:S->v8->v7->v6->v12->v13->v11->T 路径距离:229.0611 最短路径坐标:S->(60,164)->(66,160)->(102,142)->(134,98)->(136,94)->(140,94)->T 最短距离:173.8157
相关文章:

基于蚁群算法的二维路径规划算法(matlab)
微♥关注“电击小子程高兴的MATLAB小屋”获得资料 一、理论基础 1、路径规划算法 路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径。路径规划算法较多,大体上可分为全局路径规划算法和局部路径规划算法两大类。其…...
政务云参考技术架构
行业优势 总体架构 政务云平台技术框架图,由机房环境、基础设施层、支撑软件层及业务应用层组成,在运维、安全和运营体系的保障下,为政务云使用单位提供统一服务支撑。 功能架构 标准双区隔离 参照国家电子政务规范,打造符合标准的…...

android 13 aosp 预置so库
展讯对应的main.mk配置 device/sprd/qogirn**/ums***/product/***_native/main.mk $(call inherit-product-if-exists, vendor/***/build.mk)vendor/***/build.mk PRODUCT_PACKAGES \libtestvendor///Android.bp cc_prebuilt_library_shared{name:"libtest",srcs:…...

mongo篇---mongoDB Compass连接数据库
mongo篇—mongoDB Compass连接数据库 mongoDB笔记 – 第一条 一、mongoDB Compass连接远程数据库,配置URL。 URL: mongodb://username:passwordhost:port点击connect即可。 注意:host最好使用名称,防止出错连接超时。...

基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真,输出收敛曲线以及三维曲面最高点搜索结果。 2.测试软件版本以及运行结果展示 MATLAB2022A版本…...

前端js解析websocket推送的gzip压缩json的Blob数据
主要依赖插件pako https://www.npmjs.com/package/pako 1、安装 npm install pako 2、使用, pako.inflate(reader.result, {to: "string"}) 解压后的string 对象,需要JSON.parse转成json this.ws.onmessage (evt) > {console.log("…...
【wiki知识库】06.文档管理接口的实现--SpringBoot后端部分
目录 一、🔥今日目标 二、🎈SpringBoot部分类的添加 1.调用MybatisGenerator 2.添加DocSaveParam 3.添加DocQueryVo 三、🚆后端新增接口 3.1添加DocController 3.1.1 /all/{ebokId} 3.1.2 /doc/save 3.1.3 /doc/delete/{idStr} …...

c,c++,go语言字符串的演进
#include <stdio.h> #include <string.h> int main() {char str[] {a,b,c,\0,d,d,d};printf("string:[%s], len:%d \n", str, strlen(str) );return 0; } string:[abc], len:3 c语言只有数组的概念,数组本身没有长度的概念,需…...
vue-cli 快速入门
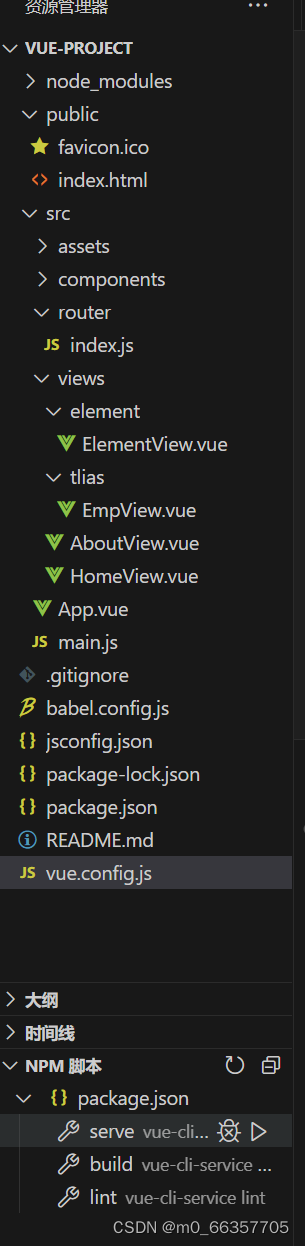
vue-cli (目前向Vite发展) 介绍:Vue-cli 是Vue官方提供一个脚手架,用于快速生成一个Vue的项目模板。 Vue-cli提供了如下功能: 统一的目录结构 本地调试 热部署 单元测试 集成打包上线 依赖环境:NodeJ…...

机器人--矩阵运算
两个矩阵相乘的含义 P点在坐标系B中的坐标系PB,需要乘以B到A到变换矩阵TAB。 M点在B坐标系中的位姿MB,怎么计算M在A中的坐标系? 两个矩阵相乘 一个矩阵*另一个矩阵的逆矩阵...

期末复习【汇总】
期末复习【汇总】 前言版权推荐期末复习【汇总】最后 前言 2024-5-12 20:52:17 截止到今天,所有期末复习的汇总 以下内容源自《【创作模板】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此话 本文首次发布于CSDN平台 作者是CSDN日星月云 博客主页是ht…...
- CONNACK Packet)
【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet
【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet 文章目录 【IM即时通讯】MQTT协议的详解(3)- CONNACK Packet前言说明一、固定同步详解、可变头部详解总结 前言 关于所有的类型的数据示例已经在上面一篇博客说完: …...

Linux - 深入理解/proc虚拟文件系统:从基础到高级
文章目录 Linux /proc虚拟文件系统/proc/self使用 /proc/self 的优势/proc/self 的使用案例案例1:获取当前进程的状态信息案例2:获取当前进程的命令行参数案例3:获取当前进程的内存映射案例4:获取当前进程的文件描述符 /proc中进程…...
Django DeleteView视图
Django 的 DeleteView 是一个基于类的视图,用于处理对象的删除操作。 1,添加视图函数 Test/app3/views.py from django.shortcuts import render# Create your views here. from .models import Bookfrom django.views.generic import ListView class B…...

代码杂谈 之 pyspark如何做相似度计算
在 PySpark 中,计算 DataFrame 两列向量的差可以通过使用 UDF(用户自定义函数)和 Vector 类型完成。这里有一个示例,展示了如何使用 PySpark 的 pyspark.ml.linalg.Vectorspyspark.sql.functions.udf 来实现这一功能:…...
混剪素材哪里找?分享8个热门素材网站
今天我们来深入探讨如何获取高质量的混剪素材,为您的短视频和自媒体制作提供最佳资源。在这篇指南中,我将介绍几个热门的素材网站,让您轻松掌握素材获取的技巧,并根据百度SEO排名规则,优化关键词的使用,确保…...

临床应用的深度学习在视网膜疾病的诊断和转诊中的应用| 文献速递-视觉通用模型与疾病诊断
Title 题目 Clinically applicable deep learning for diagnosis and referral in retinal disease 临床应用的深度学习在视网膜疾病的诊断和转诊中的应用 01 文献速递介绍 诊断成像的数量和复杂性正在以比人类专家可用性更快的速度增加。人工智能在分类一些常见疾病的二…...

中继器简介
一、网络信号衰减问题 现在的网路信号有两种,一种是电信号,另一种的光信号,电信号在网线、电话线或者电视闭路线中传输,光信号在光缆中传输,但是不管是以那种信号进行传输,随着传输距离的增加,电…...

websocket 前端项目js示例
websocket前端 和服务端websocket通信示例, 前端直接使用h5的内置对象 WebSocket 来创建和管理 WebSocket 连接,以及可以通过该连接发送和接收数据。 这个对象都是是事件方式来处理和与后端交互数据, 他们分别是 onopen打开, onclose关闭, o…...
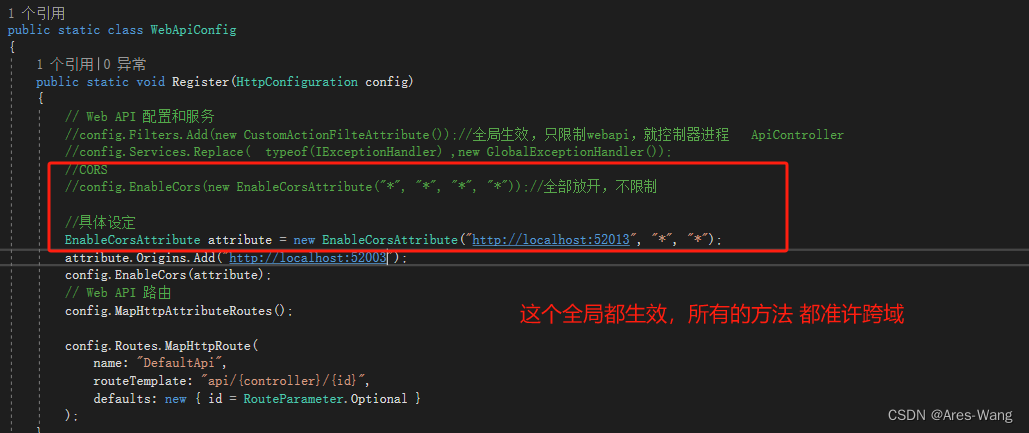
webapi跨越问题
由于浏览器存在同源策略,为了防止 钓鱼问题,浏览器直接请求才不会有跨越的问题 浏览器要求JavaScript或Cookie只能访问同域下的内容 浏览器也是一个应用程序,有很多限制,不能访问和使用电脑信息(获取cpu、硬盘等&#…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
