C/C++ 进阶(6)红黑树
个人主页:仍有未知等待探索-CSDN博客
专题分栏:C++
目录
一、概念
性质
二、操作
插入
情况一:cur为红、p为红、g为黑,如果u存在且为红
步骤:
情况二:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
情况a步骤:
情况b步骤:
情况三:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
步骤:
三、总代码
一、概念
红黑树是一颗特殊的二叉搜索树。红黑树虽然不要求是平衡的,但是该树的最长路径不超过最短路径的二倍。
红黑树避免了过多的旋转问题。
性质
1、每个节点的颜色不是红色就是黑色。
2、根节点的颜色是黑色。
3、如果一个节点的颜色是红色,则该节点的左右孩子节点都是黑色。
4、对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点。
5、每个叶子节点(这里的叶子节点指的是null节点)的颜色都是黑色的。
二、操作
插入
插入一个新节点之后,会遇到几种情况,需要我们自己对红黑树进行调整,来保证其性质的正确。
新插入节点的颜色为红色。如果为黑色的话,性质4可能会不满足,相较于性质3来说,调整起来会比较麻烦。
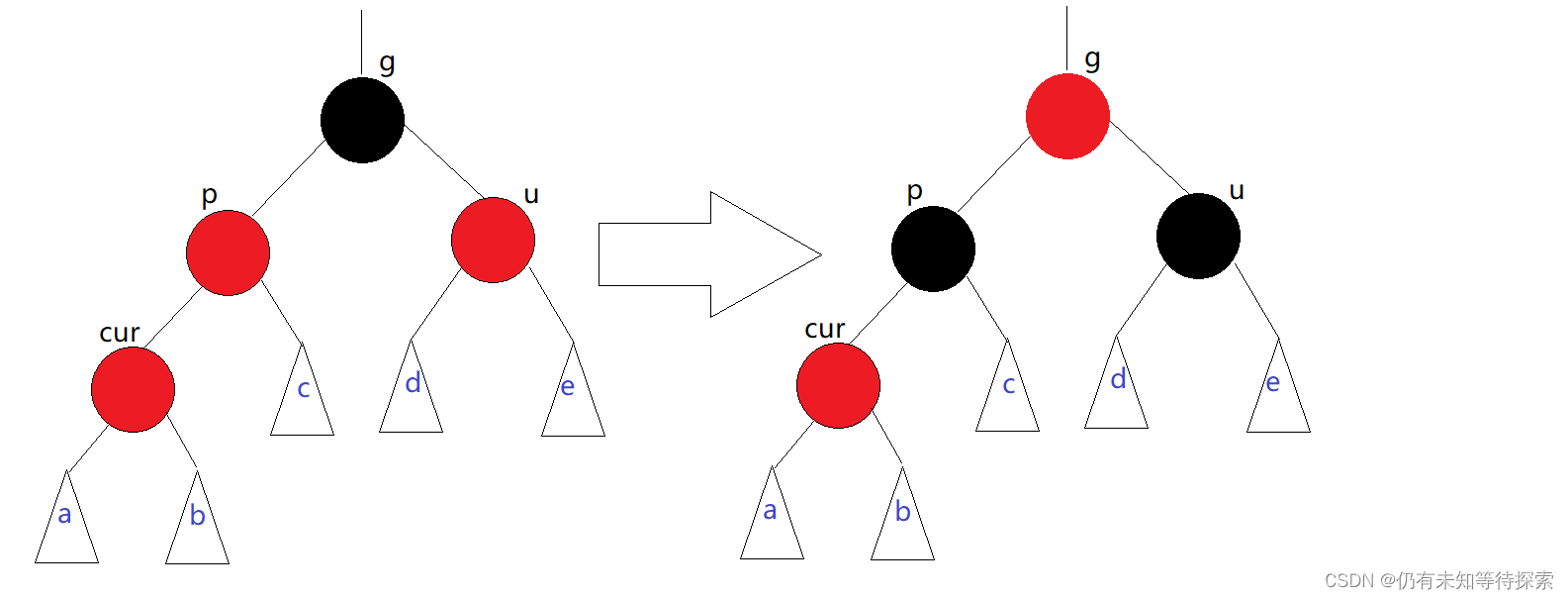
情况一:cur为红、p为红、g为黑,如果u存在且为红
步骤:
- 将 p、u 变成黑色,g 变成红色。
- 如果 g 为整个树的根节点,则将 g 变成黑色。
- 如果 g 不是根节点,且双亲结点为红色的话,继续向上进行变换。
- 如果 g 不是根节点,且双亲结点为黑色的话,则结束。
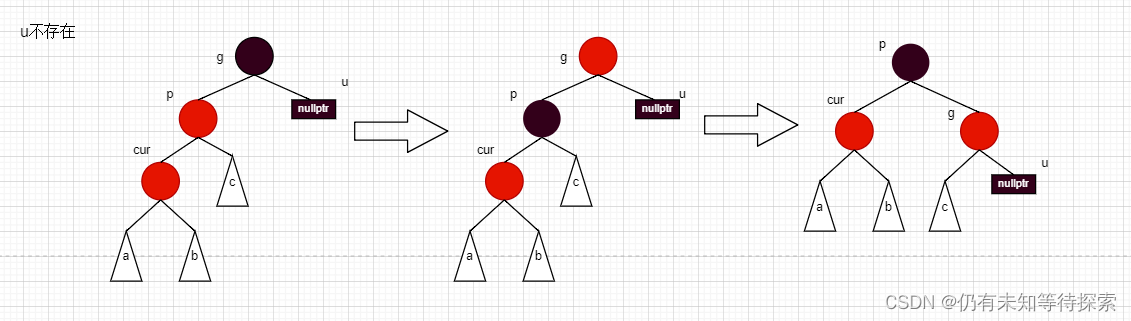
情况二:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
对于这个情况二,还有两种不同的情况。注:p 节点一定是 cur 节点的双亲结点。
情况a:cur 为 p 的左孩子,p 为 g 的左孩子。
情况b:cur 为 p 的右孩子、p 为 g 的右孩子。
情况a步骤:
- 将 p 变成黑色,g 变成红色。
- 以 g 为旋转点,进行右单旋。
情况b步骤:
- 将 p 变成黑色,g 变成红色。
- 然后以 g 为旋转点,进行左单旋。
另外一种情况,u 不存在,就需要自己去琢磨咯。
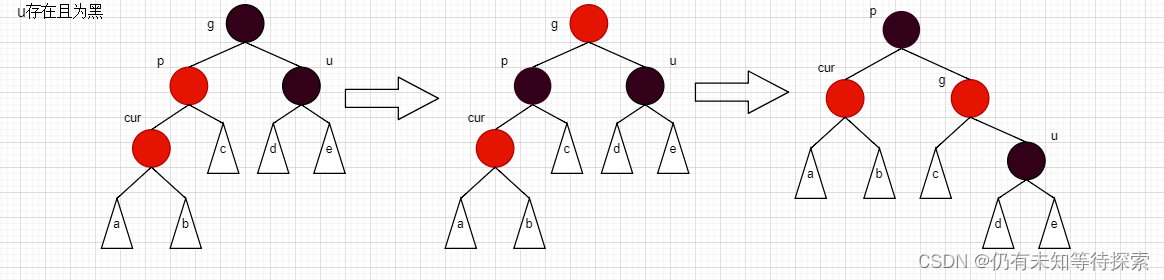
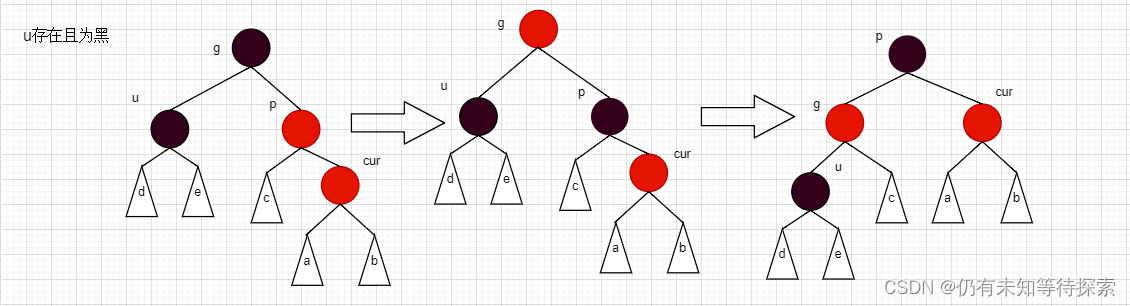
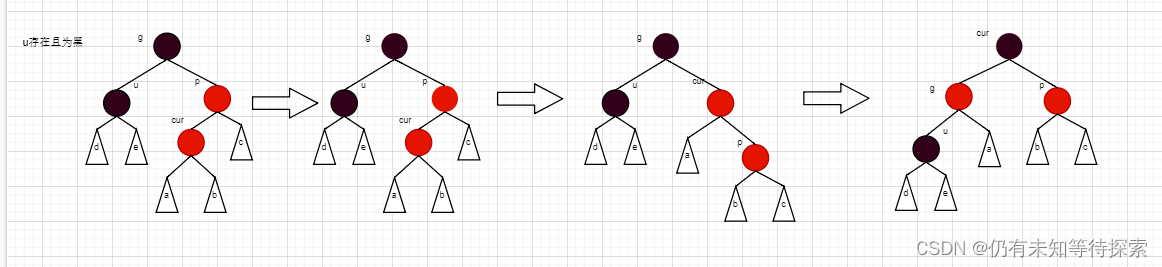
情况三:cur为红、p为红、g为黑,如果u不存在或者u存在且为黑
情况三是情况二的补充。对于情况二,我们只讲了上述的两种情况。剩余的情况则在这里进行解释。
情况a:cur 为 p 的左孩子,p 为 g 的右孩子。
情况b:cur 为 p 的右孩子、p 为 g 的左孩子。
对于上述情况,想必大概也能猜测出来,这种情况要对红黑树进行双旋处理了。这里仅对情况a 且 u 存在进行画图分析。
步骤:
- 先以 p 为旋转点进行右单旋,然后再以 g 为旋转点进行左单旋。
- 然后将 cur 变成黑色,g 变成红色。
三、总代码
#include <iostream>
#include <assert.h>
#include <vector>
using namespace std;enum color
{Red,Black
};
template <class K, class V>
struct RBTreeNode
{typedef pair<K, V> PKV;RBTreeNode(const PKV& e = PKV()):_left(nullptr),_right(nullptr),_parent(nullptr),_col(Red),_val(e){}struct RBTreeNode<K, V>* _left;struct RBTreeNode<K, V>* _right;struct RBTreeNode<K, V>* _parent;int _col;PKV _val;
};template<class K, class V>
class RBTree
{
public:typedef RBTreeNode<K, V> node;typedef pair<K, V> PKV;RBTree():_root(nullptr){}void insert(const PKV& e){// 根据二叉搜索树插入的方式进行插入node* cur = _root;node* parent = cur;while (cur){parent = cur;if (cur->_val.first > e.first){cur = cur->_left;}else{cur = cur->_right;}}cur = new node(e);if (parent == nullptr){_root = cur;}else{if (parent->_val.first > cur->_val.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;}// 更新,对于不同的情况,进行不同的调整// parent 为黑、不存在,结束node* p = parent;while (p && p->_col == Red){node* g = p->_parent;if (g->_left == p){node* u = g->_right;// 叔叔存在且为红if (u && u->_col == Red){p->_col = u->_col = Black;g->_col = Red;// 继续往上处理cur = g;p = cur->_parent;}// 叔叔不存在且为黑else {// g// p u// cif (cur == p->_left){// 右单旋RotateR(g);// 变色g->_col = Red;p->_col = Black;}// g// p u// celse {// 左右双旋RotateL(p);RotateR(g);// 变色cur->_col = Black;g->_col = Red;}// 叔叔不存在或者存在且为黑调整完,就不需要继续进行调整了break;}}else{node* u = g->_left;if (u && u->_col == Red){p->_col = u->_col = Black;g->_col = Red;// 继续往上处理cur = g;p = cur->_parent;}else {// g// u p// cif (cur == p->_right){// 左单旋RotateL(g);// 变色g->_col = Red;p->_col = Black;}// g// u p// celse {// 左右双旋RotateR(p);RotateL(g);// 变色cur->_col = Black;g->_col = Red;}// 叔叔不存在或者存在且为黑调整完,就不需要继续进行调整了break;}}}_root->_col = Black;}void inorder(){_inorder(_root);}
private:void _inorder(node* root){if (root == nullptr) return;_inorder(root->_left);cout << root->_val.first << " ";_inorder(root->_right);}void RotateR(node* parent){node* subl = parent->_left;node* sublr = subl->_right;node* grandfather = parent->_parent;parent->_left = sublr;if (sublr){sublr->_parent = parent;}subl->_right = parent;parent->_parent = subl;subl ->_parent = grandfather;if (_root == parent){if (grandfather->_left == parent){grandfather->_left = subl;}else{grandfather->_right = subl;}}else{_root = subl;}}void RotateL(node* parent){node* subr = parent->_right;node* subrl = subr->_left;node* grandfather = parent->_parent;parent->_right = subrl;if (subrl){subrl->_parent = parent;}subr->_left = parent;parent->_parent = subr;subr ->_parent = grandfather;if (_root != parent){if (grandfather->_left == parent){grandfather->_left = subr;}else{grandfather->_right = subr;}}else{_root = subr;}}protected:node* _root;
};相关文章:
C/C++ 进阶(6)红黑树
个人主页:仍有未知等待探索-CSDN博客 专题分栏:C 目录 一、概念 性质 二、操作 插入 情况一:cur为红、p为红、g为黑,如果u存在且为红 步骤: 情况二:cur为红、p为红、g为黑,如果u不存在或…...

【Vue】构建vuex-cart模块
说明:既然明确数据要存 vuex,建议分模块存,购物车数据存 cart 模块,将来还会有 user 模块,article 模块… 新建 store/modules/cart.js 挂载到 vuex 仓库上 store/cart.js import Vue from vue import Vuex from vu…...

如何成为嵌入式系统工程师?
各位朋友,如果你们有意向投身于嵌入式开发领域,那么强烈建议你们在软件和硬件两个方面均展开深入且全面的学习。 嵌入式计算机作为嵌入式系统的核心技术支撑,其是直接面向用户、产品以及应用的,无论是软件还是硬件方面都能发挥重要…...

【AI大模型】Transformers大模型库(七):单机多卡推理之device_map
目录 一、引言 二、单机多卡推理之device_map 2.1 概述 2.2 自动配置,如device_map"auto" 2.3 手动配置,如device_map"cuda:1" 三、总结 一、引言 这里的Transformers指的是huggingface开发的大模型库&#x…...

驱动代码编写(一)
驱动程序的作用 驱动程序是指与硬件设备和操作系统进行通信的软件。它的主要功能有以下几个方面: 提供硬件支持:驱动程序允许操作系统与硬件设备进行通信,以便正确地操作和控制硬件设备。它可以向操作系统提供有关硬件设备的各种信息&#x…...

Prompt-to-Prompt Image Editing with Cross Attention Control
Prompt-to-Prompt Image Editing with Cross Attention Control (P2P) Amir Hertz, Tel Aviv University, ICLR23, Paper, Code 1. 前言 编辑对这些生成模型来说是具有挑战性的,因为编辑技术的一个固有特性是保留大部分原始图像,而在基于文本的模型中…...

实验11 OSPF协议配置
实验11 OSPF协议配置 一、OSPF单区域配置(一)原理描述(二)实验目的(三)实验内容(四)实验配置(五)实验步骤 二、OSPF多区域配置(一)原理…...
ChatGPT-4o, 腾讯元宝,通义千问对比测试中文文化
国内的大模型应用我选择了国内综合实力最强的两个,一个是腾讯元宝,一个是通义千问。其它的豆包,Kimi,文心一言等在某些领域也有强于竞品的表现。 问一个中文文化比较基础的问题,我满以为中文文化chatGPT不如国内的大模型。可事实…...

node.js学习
node.js学习实操及笔记 温故node.js,node.js学习实操过程及笔记~ node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记 为什么学node.js 可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vue react angular离不开node.js …...

python将一个图片雕刻镂空成二维码
本文使用创作助手。 要将一个图片雕刻镂空成二维码,你可以使用Python中的Pillow库来处理图像,并使用qrcode库来生成二维码。以下是一个示例代码,用于将图片雕刻镂空成二维码: import qrcode from PIL import Image# 打开待处理的…...
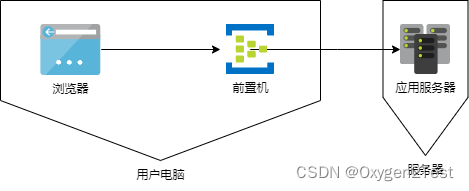
OS进程取样器OS Process Sampler执行CMD/Shell命令
Apache JMeter - Users Manual: Component Reference 1.背景 项目上最近需要测试一种很少用到的DICOM协议,但是网上资料很少,基本上可以总结为三种方案: 直接发送TCP 16进制数据包,但是参数化数据准备难度大通过开发封装jar包发送,需要开发组提供通过发送cmd命令给前置机…...

excel两个数据表格,怎样实现筛选的联动?
如图,想要通过处理器或者像素条件进行筛选,形成一个右边图2的对比表,如何实现实现联动显示呢? 这个在excel里可以借用数据透视表切片器来完成。步骤如下: 1.添加表 选中数据区域中任意一个单元格,点击 插…...

python,django好的get和post请求
获得get请求 df request.GET.get("dades")获得post请求 文件settings.py关闭csrf MIDDLEWARE [ ‘django.middleware.security.SecurityMiddleware’, ‘django.contrib.sessions.middleware.SessionMiddleware’, ‘django.middleware.common.CommonMiddleware’…...

volatile的用法
目录 前言 使用volatile的注意事项: 示例: 总结: 前言 在嵌入式C编程中,volatile是一个关键字,它用于告知编译器被修饰的变量可能会在程序的任何地方、任何时候被不可预见的、非程序本身控制的因素所改变。这通常…...

MySQL 与 PostgreSQL 关键对比二(SQL语法)
目录 1 详细示例 1.1自动增量列 1.2 字符串连接 1.3 JSON 支持 2 总结 MySQL 和 PostgreSQL 是两种流行的开源关系数据库管理系统(RDBMS)。尽管它们在许多方面相似,但在 SQL 语法和功能上存在一些显著差异。 以下SQL语句的执行如果需要开…...

徐州服务器租用该如何维护?
服务器能够帮助企业处理网络上大部分的数据和信息,在互联网行业中起着十分重要的作用,服务器的存在能够保障网站稳定的运行,主要是由内存、硬盘和处理器等组成,服务器除了进行正常的工作运行,还需要定期维护和管理&…...
—— 栈)
C++习题精选(4)—— 栈
目录 1. 最小栈2. 栈的压入弹出序列3. 逆波兰表达式求值 1. 最小栈 题目描述:设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。实现 MinStack 类: MinStack() 初始化堆栈对象。 void push(int val) 将元素…...
)
Web前端ES6-ES13笔记合集(下)
#### 五.ES10新特性 ##### 1. Object.fromEntries > Object.fromEntries()方法允许你轻松地将键值对列表转换为对象 js const arr [["name", "kerwin"], ["age", 100]]; console.log(Object.fromEntries(arr))//{name: kerwin, age: 100} …...

我要成为算法高手-双指针篇
目录 什么是双指针?问题1:移动零问题2:复写零问题3:快乐数问题4:盛最多水的容器问题5:有效三角形个数问题6:查找总价格和为目标值的两个商品(两数之和)问题7:三数之和问题8:四数之和…...
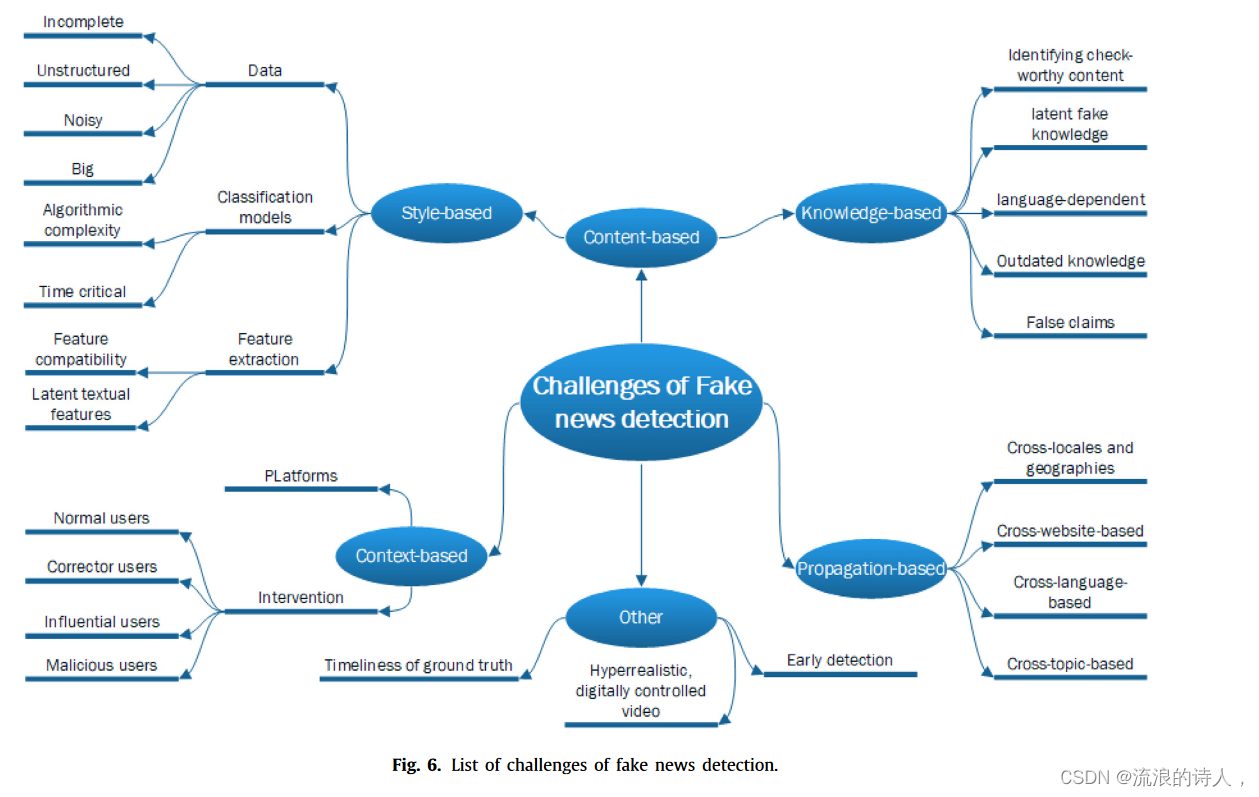
Fake news detection: A survey of graph neural network methods
abstract 各种社交网络的出现产生了大量的数据。捕获、区分和过滤真假新闻的有效方法变得越来越重要,特别是在 COVID-19 大流行爆发之后。本研究对假新闻检测系统的图神经网络 (GNN) 的现状和挑战进行了多方面、系统的回顾,并概述了使用 GNN 实现假新闻…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果