DeepSORT(目标跟踪算法)中自由度决定卡方分布的形状
DeepSORT(目标跟踪算法)中自由度决定卡方分布的形状
flyfish
重要的两个点
自由度决定卡方分布的形状(本文)
马氏距离的平方在多维正态分布下服从自由度为 k 的卡方分布
独立的信息
在统计学中,独立的信息是指数据中的独立变量或值的数量。当我们计算样本统计量(如平均值或方差)时,某些数据点的值可以从其他数据点和统计量中推导出来,因此这些点不再提供独立的信息。
卡方分布是一种统计学上的概率分布,通常用于假设检验,比如检验数据的独立性或适合度。卡方分布描述的是一个变量的值如何分布,特别是当这些变量表示方差或者是两个变量之间的独立性时。它的形状取决于自由度(degree of freedom, df),自由度越高,分布越接近正态分布。
绘制几个不同自由度下的卡方分布
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats# 定义自由度
dfs = [1, 2, 3, 5, 10]# 设置x轴范围
x = np.linspace(0, 20, 1000)# 创建图形
plt.figure(figsize=(10, 6))# 绘制不同自由度的卡方分布曲线
for df in dfs:plt.plot(x, stats.chi2.pdf(x, df), label=f'df={df}')# 添加图例和标签
plt.legend()
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Chi-Square Distribution')
plt.grid(True)# 显示图形
plt.show()

卡方分布图:
- df=1:分布最偏,右侧有长尾。
- df=2:开始向左侧移动,但仍有右侧长尾。
- df=3:分布更集中,右侧长尾减弱。
- df=5:分布更靠近正态分布,右侧尾巴更短。
- df=10:非常接近正态分布,右侧尾巴很短。
这种图形有助于理解自由度对卡方分布形状的影响。随着自由度增加,卡方分布逐渐向正态分布靠拢。
卡方分布的公式
可以用以下数学表达式来表示:
f ( x ; k ) = 1 2 k / 2 Γ ( k / 2 ) x k / 2 − 1 e − x / 2 f(x; k) = \frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2-1} e^{-x/2} f(x;k)=2k/2Γ(k/2)1xk/2−1e−x/2
其中:
- x x x 是卡方变量(取非负值)。
- k k k 是自由度(degrees of freedom)。
- Γ \Gamma Γ 是伽玛函数(Gamma function),它是阶乘函数的一种扩展,满足 Γ ( n ) = ( n − 1 ) ! \Gamma(n) = (n-1)! Γ(n)=(n−1)! 对于正整数 n n n。
伽玛函数 (Gamma function)
伽玛函数是一种特殊函数,它是阶乘函数在非整数值上的扩展。对于一个正整数 n n n,伽玛函数 Γ ( n ) \Gamma(n) Γ(n) 等于 ( n − 1 ) ! (n-1)! (n−1)!。伽玛函数的定义是:
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt Γ(z)=∫0∞tz−1e−tdt
当 z z z 是正整数时,伽玛函数满足 Γ ( n ) = ( n − 1 ) ! \Gamma(n) = (n-1)! Γ(n)=(n−1)!。
通常自由度等于数据点的数量减去你计算中所涉及的参数数量。
例如:
- 样本的平均值计算:
- 你有 n n n 个数据点。
- 计算平均值需要一个参数(就是这个平均值)。
- 因此,自由度是 n − 1 n-1 n−1。
- 线性回归:
- 假设你有 n n n 个数据点和两个参数(斜率和截距)。
- 自由度是 n − 2 n-2 n−2。
假设我们有5个数据点 x 1 , x 2 , x 3 , x 4 , x 5 x_1, x_2, x_3, x_4, x_5 x1,x2,x3,x4,x5:
- 计算平均值:
x ˉ = x 1 + x 2 + x 3 + x 4 + x 5 5 \bar{x} = \frac{x_1 + x_2 + x_3 + x_4 + x_5}{5} xˉ=5x1+x2+x3+x4+x5 - 计算每个数据点的偏差(数据点与平均值的差):
d 1 = x 1 − x ˉ d_1 = x_1 - \bar{x} d1=x1−xˉ
d 2 = x 2 − x ˉ d_2 = x_2 - \bar{x} d2=x2−xˉ
d 3 = x 3 − x ˉ d_3 = x_3 - \bar{x} d3=x3−xˉ
d 4 = x 4 − x ˉ d_4 = x_4 - \bar{x} d4=x4−xˉ
d 5 = x 5 − x ˉ d_5 = x_5 - \bar{x} d5=x5−xˉ
偏差的和为零:
d 1 + d 2 + d 3 + d 4 + d 5 = 0 d_1 + d_2 + d_3 + d_4 + d_5 = 0 d1+d2+d3+d4+d5=0
这表明,知道了前4个偏差 d 1 , d 2 , d 3 , d 4 d_1, d_2, d_3, d_4 d1,d2,d3,d4 后,第5个偏差 d 5 d_5 d5 是可以通过前4个偏差计算出来的,因为偏差的总和必须为零:
d 5 = − ( d 1 + d 2 + d 3 + d 4 ) d_5 = - (d_1 + d_2 + d_3 + d_4) d5=−(d1+d2+d3+d4)
这说明第5个偏差并不是独立的,它依赖于前4个偏差。
自由度的减少
当我们计算平均值时,我们使用了所有数据点的信息,这个平均值本身是由这些数据点计算出来的,因此在计算方差时,有一个数据点的信息量不再是独立的(因为它可以从其他数据点和平均值推导出来)。这就是为什么在计算方差时,自由度是 n − 1 n-1 n−1。
无论最后一个数据点是大是小,这个推理过程都成立。因为平均值 x ˉ \bar{x} xˉ 是所有数据点的一个函数,在计算方差时,所有数据点与平均值的偏差和为零:
∑ i = 1 n ( x i − x ˉ ) = 0 \sum_{i=1}^{n} (x_i - \bar{x}) = 0 i=1∑n(xi−xˉ)=0
这表明,如果你知道 n − 1 n-1 n−1 个偏差,那么最后一个偏差是可以通过前面 n − 1 n-1 n−1 个偏差计算出来的。因此,总共有 n − 1 n-1 n−1 个独立的信息,这就是我们在计算样本方差时为什么使用 n − 1 n-1 n−1 作为分母。
自由度的作用
-
调整估计偏差:
使用自由度调整计算可以消除估计过程中的偏差,使得估计结果更加准确。例如,样本方差的计算使用 n − 1 n-1 n−1 作为分母,使其成为总体方差的无偏估计。 -
反映数据独立性:
自由度表示数据集中独立信息的数量。在统计计算中,自由度反映了可以自由变动的数据点数量,而不受其他数据点或估计参数的约束。 -
决定分布形状:
在假设检验中,自由度决定了统计量的分布形状,如卡方分布。不同的自由度会导致分布形状不同,从而影响显著性水平和置信区间的计算。
要深入理解样本方差、总体方差以及无偏估计的概念,首先需要了解一些基础定义和背景知识。让我们逐一解释这些概念。
样本方差、总体方差、无偏估计
总体方差(Population Variance):
总体方差是描述总体数据的离散程度的度量,表示总体数据点与总体均值之间的平均平方偏差。假设总体中有 N N N 个数据点 X 1 , X 2 , … , X N X_1, X_2, \ldots, X_N X1,X2,…,XN,总体方差的计算公式为:
σ 2 = 1 N ∑ i = 1 N ( X i − μ ) 2 \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (X_i - \mu)^2 σ2=N1∑i=1N(Xi−μ)2
其中, μ \mu μ 是总体的平均值。
样本方差(Sample Variance):
样本方差是从样本数据中估计总体方差的度量,表示样本数据点与样本均值之间的平均平方偏差。假设样本中有 n n n 个数据点 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn,样本方差的计算公式为:
s 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 s2=n−11∑i=1n(xi−xˉ)2
其中, x ˉ \bar{x} xˉ 是样本的平均值。
无偏估计(Unbiased Estimator)
一个估计量是无偏的,如果其期望值等于所要估计的总体参数。即,对于样本方差 s 2 s^2 s2 来说,当它作为总体方差 σ 2 \sigma^2 σ2 的估计时,满足以下条件:
E [ s 2 ] = σ 2 \mathbb{E}[s^2] = \sigma^2 E[s2]=σ2
其中, E \mathbb{E} E 表示期望值。
举例子
使用总体数据 2 , 4 , 6 , 8 , 10 2, 4, 6, 8, 10 2,4,6,8,10 来计算总体方差和样本方差。
总体方差
- 计算总体平均值:
μ = 2 + 4 + 6 + 8 + 10 5 = 6 \mu = \frac{2 + 4 + 6 + 8 + 10}{5} = 6 μ=52+4+6+8+10=6 - 计算每个数据点的平方偏差:
( 2 − 6 ) 2 = 16 (2 - 6)^2 = 16 (2−6)2=16
( 4 − 6 ) 2 = 4 (4 - 6)^2 = 4 (4−6)2=4
( 6 − 6 ) 2 = 0 (6 - 6)^2 = 0 (6−6)2=0
( 8 − 6 ) 2 = 4 (8 - 6)^2 = 4 (8−6)2=4
( 10 − 6 ) 2 = 16 (10 - 6)^2 = 16 (10−6)2=16 - 计算总体方差:
σ 2 = 1 5 ( 16 + 4 + 0 + 4 + 16 ) = 40 5 = 8 \sigma^2 = \frac{1}{5} (16 + 4 + 0 + 4 + 16) = \frac{40}{5} = 8 σ2=51(16+4+0+4+16)=540=8
样本方差的无偏估计
假设我们抽取多个样本,每个样本包含3个数据点:
样本 1: 2 , 4 , 6 2, 4, 6 2,4,6
-
样本平均值:
x ˉ 1 = 2 + 4 + 6 3 = 4 \bar{x}_1 = \frac{2 + 4 + 6}{3} = 4 xˉ1=32+4+6=4 -
平方偏差:
( 2 − 4 ) 2 = 4 (2 - 4)^2 = 4 (2−4)2=4
( 4 − 4 ) 2 = 0 (4 - 4)^2 = 0 (4−4)2=0
( 6 − 4 ) 2 = 4 (6 - 4)^2 = 4 (6−4)2=4 -
样本方差(无偏估计):
s 1 2 = 1 3 − 1 ( 4 + 0 + 4 ) = 8 2 = 4 s^2_1 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4 s12=3−11(4+0+4)=28=4
样本 2: 4 , 6 , 8 4, 6, 8 4,6,8 -
样本平均值:
x ˉ 2 = 4 + 6 + 8 3 = 6 \bar{x}_2 = \frac{4 + 6 + 8}{3} = 6 xˉ2=34+6+8=6 -
平方偏差:
( 4 − 6 ) 2 = 4 (4 - 6)^2 = 4 (4−6)2=4
( 6 − 6 ) 2 = 0 (6 - 6)^2 = 0 (6−6)2=0
( 8 − 6 ) 2 = 4 (8 - 6)^2 = 4 (8−6)2=4 -
样本方差(无偏估计):
s 2 2 = 1 3 − 1 ( 4 + 0 + 4 ) = 8 2 = 4 s^2_2 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4 s22=3−11(4+0+4)=28=4
样本 3: 6 , 8 , 10 6, 8, 10 6,8,10 -
样本平均值:
x ˉ 3 = 6 + 8 + 10 3 = 8 \bar{x}_3 = \frac{6 + 8 + 10}{3} = 8 xˉ3=36+8+10=8 -
平方偏差:
( 6 − 8 ) 2 = 4 (6 - 8)^2 = 4 (6−8)2=4
( 8 − 8 ) 2 = 0 (8 - 8)^2 = 0 (8−8)2=0
( 10 − 8 ) 2 = 4 (10 - 8)^2 = 4 (10−8)2=4 -
样本方差(无偏估计):
s 3 2 = 1 3 − 1 ( 4 + 0 + 4 ) = 8 2 = 4 s^2_3 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4 s32=3−11(4+0+4)=28=4
我们看到,不同的样本有不同的方差,但这些样本方差的平均值趋向于总体方差。这是无偏估计的意义:期望值(平均值)等于总体方差。
结论
10. 总体方差:总体所有数据点的平均平方偏差。在例子中,计算得到总体方差为 8。
11. 样本方差(无偏估计):为了估计总体方差,样本方差用 n − 1 n-1 n−1 作为分母,使其期望值等于总体方差。对于样本方差来说,使用 n − 1 n-1 n−1 作为分母确保其期望值等于总体方差。这并不意味着每一个具体的样本方差都等于总体方差,而是多个样本方差的平均值会接近于总体方差。
12. 无偏估计的意义:单个样本方差不一定等于总体方差,但多个样本方差的平均值会接近于总体方差,从而实现无偏估计的目标。无偏估计的概念是基于期望值的。当我们从总体中抽取一个样本并计算样本方差时,我们使用 n − 1 n-1 n−1 作为分母而不是 n n n。这是因为样本均值 x ˉ \bar{x} xˉ 是用所有 n n n 个数据点计算出来的,这使得样本中的偏差和为零,消耗了一个自由度。使用 n − 1 n-1 n−1 可以使样本方差成为总体方差的无偏估计。
通过无偏估计,确保在长远来看,估计值不会系统性地偏离真实值。
相关文章:

DeepSORT(目标跟踪算法)中自由度决定卡方分布的形状
DeepSORT(目标跟踪算法)中自由度决定卡方分布的形状 flyfish 重要的两个点 自由度决定卡方分布的形状(本文) 马氏距离的平方在多维正态分布下服从自由度为 k 的卡方分布 独立的信息 在统计学中,独立的信息是指数据…...
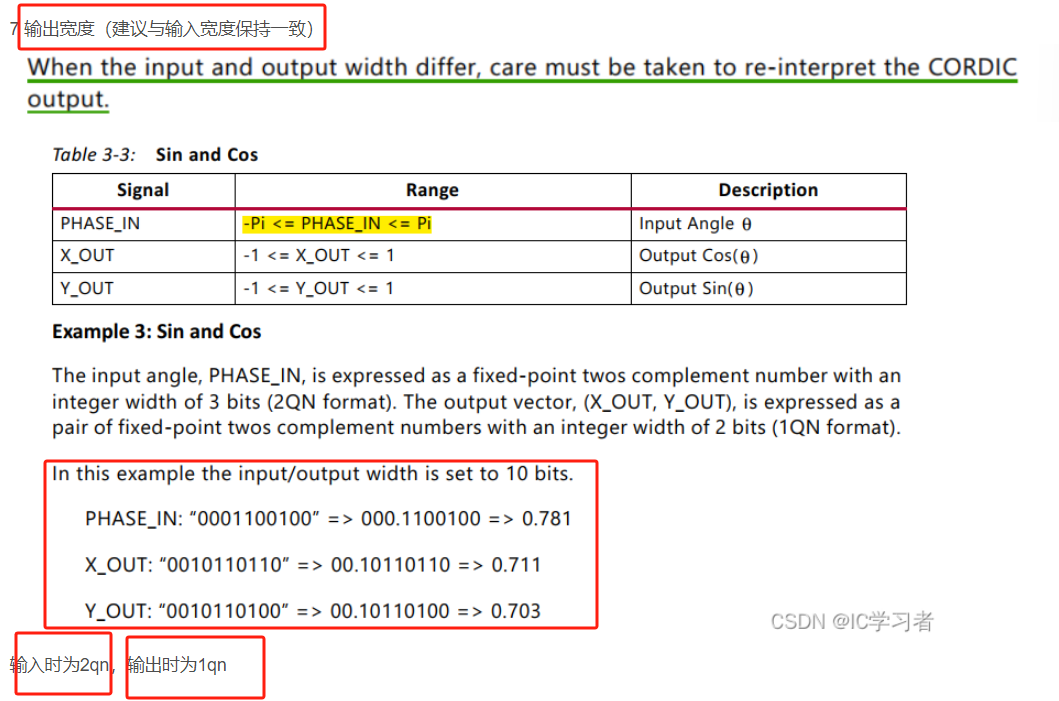
cordic IP核中,sin and cos的使用
参考视频:FPGA IP之CORDIC_哔哩哔哩_bilibili FPGA IP之CORDIC使用与仿真_哔哩哔哩_bilibili 一、参数说明 functional selection rotate是旋转,sin and cos是计算这两个三角函数,sinh和cosh是计算双曲正弦和双曲余弦 phase format 对于…...
SpringSecurity入门(三)
12、密码加密 12.1、不指定具体加密方式,通过DelegatingPasswordEncoder,根据前缀自动选择 PasswordEncoder passwordEncoder PasswordEncoderFactories.createDelegatingPasswordEncoder();12.2、指定具体加密方式 // Create an encoder with streng…...

luogu-P10570 [JRKSJ R8] 网球
题目传送门: [JRKSJ R8] 网球 - 洛谷https://www.luogu.com.cn/problem/P10570 解题思路 数学问题,暴力这个范围会超时。 首先,找出这两个数的最大公因数,将这两个数分别除以最大公因数,则这两个数互质,判…...

ASP.NET的WebService跨域CORS问题解决方案
ASP.NET WebService 跨域(CORS, Cross-Origin Resource Sharing)问题通常发生在当您尝试从不同的源(域名、协议或端口)调用 WebService 时。浏览器由于安全原因,默认会阻止此类跨域请求。为了解决这个问题,您需要在 WebService 服务器端配置 CORS。 以下是在 ASP.NET We…...

大众点评全国爱车店铺POI采集177万家-2024年5月底
大众点评全国爱车店铺POI采集177万家-2024年5月底 店铺POI点位示例: 店铺id H69Y6l1Ixs2jLGg2 店铺名称 HEEJOO豪爵足道(伍家店) 十分制服务评分 7.7 十分制环境评分 7.7 十分制划算评分 7.7 人均价格 134 评价数量 2982 店铺地址 桔城路2号盛景商业广场1-3…...

【文献阅读】LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS
目录 1. motivation2. overall3. model3.1 low rank parametrized update matrices3.2 applying lora to transformer 4. limitation5. experiment6. 代码7. 补充参考文献 1. motivation 常规的adaptation需要的微调成本过大现有方法的不足: Adapter Layers Introd…...
Rust学习06:使用CSDN的AI工具“C知道”分析代码错误
朋友们,我最近真的是在绝望的边缘了! Rust咋这么蓝涅! 资料咋这们少涅! 记得学Python的时候,基本上你遇到的所有问题都可以在书上或者网上找到答案,中文世界找不到那么在英文世界一定能找到答案。 我猜&…...
MeiliSearch-轻量级且美丽的搜索引擎
MeiliSearch-轻量级且美丽的搜索引擎 MeiliSearch 是一个功能强大、快速、开源、易于使用和部署的搜索引擎。它具有以下特点: 支持中文搜索:MeiliSearch 对中文有良好的支持,不需要额外的配置。高度可定制:搜索和索引都可以高度…...

python使用wkhtmltopdf将html字符串保存pdf,解决出现方框的问题
出现的问题: 解决办法: <html> <head><meta charset"UTF-8"/> </head> <style> * {font-family: Arial,SimSun !important; } </style> </html>在html字符串前面加上上面代码,意思是设…...
Java练习题
题目: 1. 定义长方体类Cuboid,要求如下:(1)私有成员变量包括长length、宽width和高height;(2)构造方法包括一个公共的空构造方法,一个能够初始化所有成员变量的构造方法…...

【Python/Pytorch - 网络模型】-- 手把手搭建U-Net模型
文章目录 文章目录 00 写在前面01 基于Pytorch版本的UNet代码02 论文下载 00 写在前面 通过U-Net代码学习,可以学习基于Pytorch的网络结构模块化编程,对于后续学习其他更复杂网络模型,有很大的帮助作用。 在01中,可以根据U-Net…...

Ansible-doc 命令
目录 常用参数 基本用法 查看指定模块的文档 列出所有可用模块 搜索模块 显示模块参数的简单列表 显示详细的说明和示例 详细示例 查看 file 模块的文档 简略查看 copy 模块的参数 ansible-doc 是 Ansible 中的一个非常有用的命令行工具,它可以帮助你查找…...
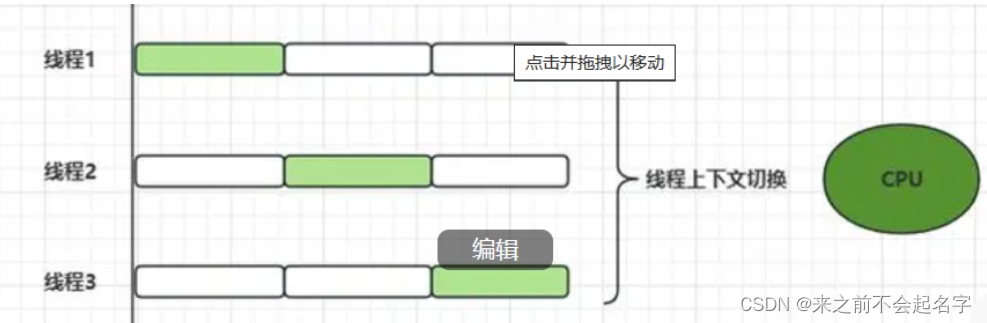
面试题:什么是线程的上下文切换?
线程的上下文切换是指在操作系统中,CPU从执行一个线程的任务切换到执行另一个线程任务的过程。在现代操作系统中,为了实现多任务处理和充分利用CPU资源,会同时管理多个线程的执行。由于CPU在任意时刻只能执行一个线程,因此需要在这…...

【简单讲解Perl语言】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

专硕初试科目一样,但各专业的复试线差距不小!江南大学计算机考研考情分析!
江南大学物联网工程学院,是由江南大学信息工程学院和江南大学通信与控制工程学院,于2009年合并组建成立“物联网工程学院”,也是全国第一个物联网工程学院。 江南大学数字媒体学院是以江南大学设计学院动画系和信息工程学院数字媒体技术系为…...

“华为Ascend 910B AI芯片挑战NVIDIA A100:效能比肩,市场角逐加剧“
华为自主研发的人工智能芯片——Ascend 910B,近期在世界半导体大会及南京国际半导体博览会上由华为ICT基础设施管理委员会执行董事、主任王涛发表声明称,该芯片在训练大规模语言模型时的效率高达80%,与NVIDIA的A100相比毫不逊色,且…...
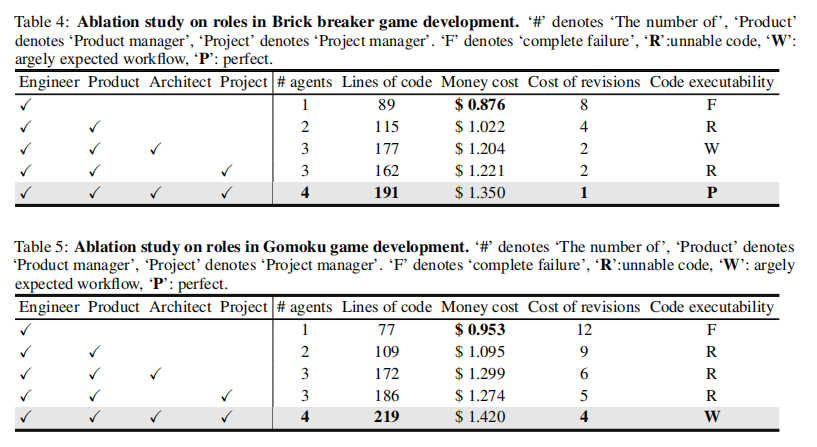
针对多智能体协作框架的元编程——METAGPT
M ETA GPT: M ETA P ROGRAMMING FOR M ULTI -A GENT COLLABORATIVE F RAMEWORK 1.概述 现有的多智能体系统主要面临以下问题: 复杂性处理不足:传统的多智能体系统主要关注简单任务,对于复杂任务的处理能力有限,缺乏深入探索和…...

Django自定义CSS
创建一个CSS文件(例如admin_custom.css),并在其中添加针对你希望修改的字段的CSS规则。在你的Django项目的settings.py文件中,添加自定义CSS文件的路径到STATICFILES_DIRS。 # settings.py STATICFILES_DIRS [ os.path.join(BA…...
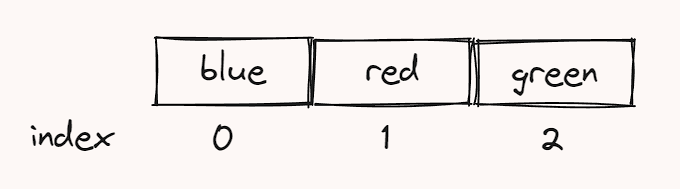
Rust基础学习-标准库
栈和堆是我们Rust代码在运行时可以使用的内存部分。Rust是一种内存安全的编程语言。为了确保Rust是内存安全的,它引入了所有权、引用和借用等概念。要理解这些概念,我们必须首先了解如何在栈和堆中分配和释放内存。 栈 栈可以被看作一堆书。当我们添加更…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
