关于Lambert W函数
来源:R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey, and D. E. Knuth, “On Lambert’s W function,” Adv. Comput. Math., vol. 5, pp. 329–359, May 1996, doi: 10.1007/BF02124750.
摘要
Lambert W函数被定义为函数 w ↦ w e w w \mapsto we^w w↦wew的多值逆函数。它在纯数学和应用数学中有许多应用,其中一些在此被简要描述。我们提供了一个关于W函数复数分支的新讨论,一个对所有分支都有效的渐近展开式,一个用于任意精度计算该函数的有效数值程序,以及一种用于包含W的表达式符号积分的方法。
文章的研究内容
文章主要研究了Lambert W函数,这是一个定义为函数 w ↦ w e w w \mapsto we^w w↦wew的多值逆函数,在纯数学和应用数学中有广泛的应用。研究内容包括以下几个方面:
-
历史背景与引言:文章追溯了Lambert W函数的历史,起源于Johann Heinrich Lambert在18世纪解决三元方程的工作。通过Euler的变换,原方程被简化为对数形式,从而引出Lambert W函数的概念。
-
复分支分析:文中详细探讨了Lambert W函数的复数域特性,给出了所有分支的解析描述,并基于de Bruijn的工作扩展了复无穷远处的渐近展开。
-
渐近展开:文章提出了一种适用于所有分支的有效渐近展开方法,适用于任意分支的W函数值计算,这一成果对于理解和逼近W函数在不同区域的行为至关重要。
-
数值计算:介绍了一种高效且精确的数值方法,用于任意精度下W函数的计算,特别是在Maple V Release 2中实现了任意精度复浮点形式的所有分支的W(z)的计算。
-
符号积分:基于K.B. Ranger的工作,文章重新发现了一种古老的积分反函数方法,使得包含W函数的一类广义函数能够进行符号积分,这是计算理论和算法设计中的一个重要进展。
-
应用实例:文章列举了W函数的多种应用案例,比如在树的计数问题、水波高度计算、随机网络连通性分析、流行病模型和算法分析中的应用等。例如,W函数在分析具有延迟项的线性常系数微分方程的解时起关键作用,以及在动态模型和计算机算法行为分析中与T函数一起出现。
-
符号约定与命名:文章提议将此函数命名为Lambert W函数,既反映了其与Lambert系列的联系,也考虑了E.M. Wright在该函数多个方面的开创性工作。在Maple系统中,W函数已实现多年,并在后续版本中提供了所有分支的任意精度实现。
整体而言,这篇文章旨在整合关于Lambert W函数的现有研究成果,并提出了新的理论进展,包括复分析、数值方法和符号计算等方面,同时也强调了其在多个学科中的实际应用价值。
文章的研究方法
文章采用的研究方法主要包括理论分析、数值计算和符号计算三个方面,以深入探讨Lambert W函数的性质及其应用。具体来说:
-
理论分析:通过对Lambert W函数的复数分支进行深入分析,研究者提出了一套新的讨论框架,这有助于理解W函数在复平面上的结构和行为。他们还推导出了一个普遍适用的渐近展开式,该展开式对所有分支都有效,为精确近似W函数提供了理论基础。
-
数值计算:为了高效准确地计算Lambert W函数,研究者比较了三种迭代法——牛顿法、Halley法(一种三阶方法)和一种四阶方法(在原始文献[30]中仅针对实数主分支进行了描述,但可以容易地推广到所有分支和复数域)。通过在Maple V Release 3平台上实现这些算法,并在DEC Alpha 3000/800S计算机上进行测试,他们发现Halley法通常是最优的,四阶方法次之,而牛顿法最慢。这些发现基于不同精度、分支和复数参数的广泛测试,证明了在实际计算环境下的有效性。
-
符号积分:文章还介绍了一种用于包含Lambert W函数的表达式的符号积分方法。这种方法基于对W函数的深入理解,允许直接处理包含W的复杂表达式的积分问题,而不必依赖数值近似,这对于理论分析尤其重要。
研究不仅加深了对Lambert W函数内在性质的理解,而且开发了实用的计算工具,使研究人员和工程师能够在各自领域中有效地利用这一多功能函数。研究过程中考虑了算法效率、精度要求以及在不同计算平台上的通用性,体现了理论与实践的紧密结合。
文章的创新点
-
复数分支的新讨论:作者对Lambert W函数的复数分支进行了新的探讨,这是前人研究中可能未充分覆盖的一个领域。这种新讨论增进了对W函数在复平面上的结构和性质的理解。
-
通用渐近展开:提出了一种适用于所有Lambert W函数分支的渐近展开式,这意味着无论在实数域还是复数域,都可以用这个展开式来近似W函数的值,提高了在不同应用场景中的实用性。
-
高效数值计算方法:开发了一种高效的数值计算程序,能够以任意精度计算Lambert W函数。这对于需要高精度计算的科学和工程应用尤为重要,如在模拟、优化问题和物理学等领域。
-
符号积分方法:引入了一种用于含有Lambert W函数的表达式的符号积分方法,这在理论分析中非常有用,因为它允许直接处理表达式而不是通过数值近似,从而保持了结果的精确性和可解析性。
-
历史与现代应用结合:通过回顾Lambert和Euler的工作,文章将历史上的数学成就与现代计算技术相结合,展示了Lambert W函数从古典问题到现代科学计算中的广泛应用,体现了数学理论与实际问题解决之间的桥梁作用。
文章的创新不仅在于理论上的深化,还包括了实用计算技术的推进,为研究者和工程师提供了一套全面的工具,以探索和利用Lambert W函数在纯数学和应用数学中的潜力。
文章的结论
-
Lambert W函数的综合研究:文章汇总了Lambert W函数的众多已知结果,为读者提供了方便的参考。通过历史回顾、应用实例以及新发现的展示,增强了对W函数在数学和科学领域重要性的认识。
-
复杂分支的深入理解:对Lambert W函数的复数分支进行了新的讨论,确定了其在复平面的渐近展开,这对于理解和计算W函数在复域中的行为至关重要。
-
高效数值计算方案:提出了一种高效且准确的数值方法,能够在Maple软件中实现任意精度的复数浮点形式的W(z)的所有分支计算。这表明,无论是理论研究还是实际应用,都能获得高精度的W函数值。
-
符号积分技术:介绍了基于K.B. Ranger的工作,重新发现了古老的积分反函数方法,该方法使得包含W函数的大类表达式能够进行符号积分。这一发现拓展了W函数在理论计算和分析中的应用范围。
-
标准符号提议:提议采用统一的标准符号表示Lambert W函数在复平面上的所有分支,以及相关的tree函数T(x),以提高该函数在各领域使用的标准化程度和认知度。同时,文章指出,由于早期使用混乱的记号和缺乏标准名称,Lambert W函数的知名度与其广泛应用不相匹配,但该文发表后,情况有所改善。
-
实践反馈与改进:文章的初次发布吸引了大量反馈,使得研究得到了实质性的改进,特别是Heck和Robinson指出了W函数与延迟微分方程的关联,增加了其应用维度。
文章不仅总结了Lambert W函数的现有知识,还推动了对其更深入的理解和应用,为该领域的研究者提供了一系列实用工具和理论支持。此外,文章还强调了标准化命名和符号表述的重要性,为促进跨学科交流和W函数的广泛认知奠定了基础。
相关文章:

关于Lambert W函数
来源:R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey, and D. E. Knuth, “On Lambert’s W function,” Adv. Comput. Math., vol. 5, pp. 329–359, May 1996, doi: 10.1007/BF02124750. 摘要 Lambert W函数被定义为函数 w ↦ w e w w \mapsto we^…...
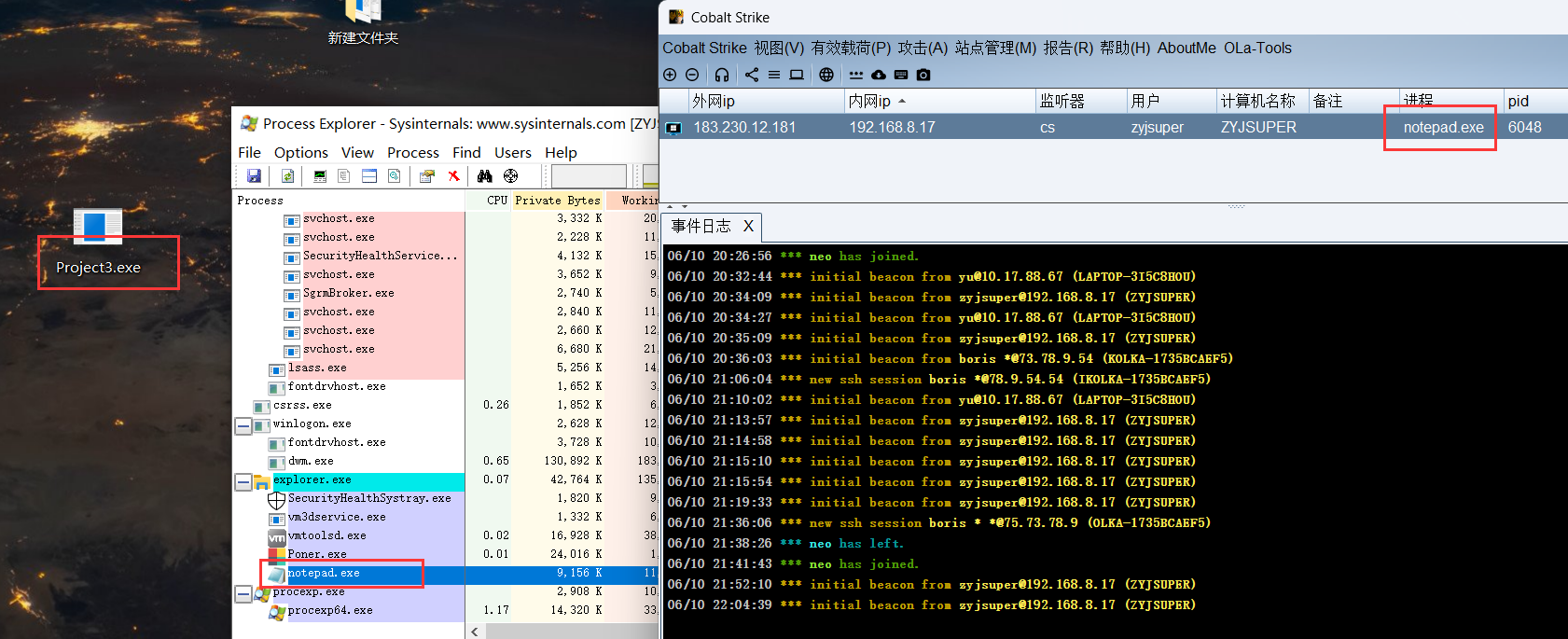
【免杀】C2远控-APC注入-进程镂空
目录 进程镂空&傀儡进程(主要过内存扫描)代码 傀儡进程演示如何上线上线演示 APC注入&进程欺骗(主要过内存扫描)同步调用与异步调用代码演示 进程镂空&傀儡进程(主要过内存扫描) 进程镂空(Pro…...
面试)
20240611 讯飞JAVA工程师(研发经理岗)面试
1.线程安全的集合类 在Java中,一些线程安全的集合类有Stack、Vector、Properties、Hashtable等 2.线程池中execute和submit的区别 1)参数及返回值不同 excute只能提交Runnable,无返回值 submit既可以提交Runnable,返回值为null&am…...

【研发日记】Matlab/Simulink软件优化(三)——利用NaNFlag为数据处理算法降阶
文章目录 前言 背景介绍 初始算法 优化算法 分析和应用 总结 前言 见《【研发日记】Matlab/Simulink软件优化(一)——动态内存负荷压缩》 见《【研发日记】Matlab/Simulink软件优化(二)——通信负载柔性均衡算法》 背景介绍 在一个嵌入式软件开发项目中,需要开…...

go语言接口之http.Handler接口
package httptype Handler interface {ServeHTTP(w ResponseWriter, r *Request) }func ListenAndServe(address string, h Handler) error ListenAndServe函数需要一个例如“localhost:8000”的服务器地址,和一个所有请求都可以分 派的Handler接口实例。它会一直运…...
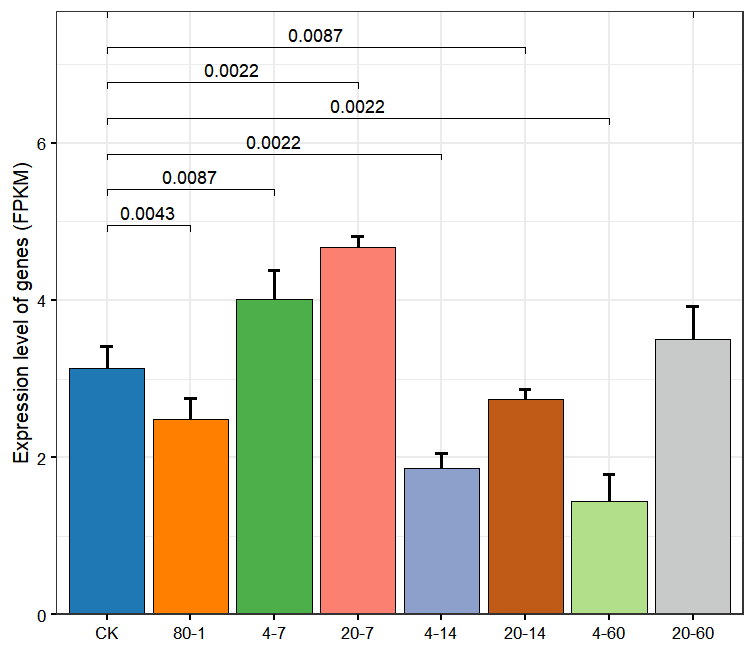
R语言 | 使用最简单方法添加显著性ggpubr包
本期教程原文:使用最简单方法添加显著性ggsignif包 本期教程 获得本期教程代码和数据,在后台回复关键词:20240605 小杜的生信笔记,自2021年11月开始做的知识分享,主要内容是R语言绘图教程、转录组上游分析、转录组下游…...

【Linux】shell脚本变量——系统变量、环境变量和用户自定义变量
系统变量 系统变量是由系统预设的,它们通常在系统启动时被加载,并对所有用户和所有shell实例都有效。这些变量通常控制着系统的行为和配置,例如PATH(命令搜索路径)、HOME(用户主目录)等。系统变…...
QWidget 属性——windowTitle·windowIcon·qrc
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 一、windowTitle二、windowIcon三、qrc 一、windowTitle windowTitle 是一个通常用于表示窗口标题…...
深入理解rtmp(一)之开发环境搭建
深入理解rtmp(一)之开发环境搭建 手机直播在15年的时候突然火起来,随着花椒,映客等出现,直播一下就出现在了风口,各个公司针对直播的战斗迅速打响,战斗过程比较短暂,随着许多公司的退出和死去,手机直播行业趋于稳定,直播服务时长也被传统的CDN厂商牢牢占据,后面大家又把精力投…...

java常用面试基础题
&与&&区别? &和&&都是逻辑运算符,都是判断两边同时真则为真,否则为假;但是&&当第一个条件不成之后,后面的条件都不执行了,而&则还是继续执行,直到整个条件…...
)
互联网摸鱼日报(2024-06-11)
互联网摸鱼日报(2024-06-11) 36氪新闻 雅诗兰黛,胆子也太大了 苹果WWDC终极前瞻:5大看点20大AI新功能,库克不能输的一战 瑞士清洁科技公司Enerdrape开发预制地热板,回收城市地下空间的浅层地热能和废热用于建筑物制热或制冷 | …...

中介子方程十二
X$XFX$XEXyXαXiX$XαXiXrXkXtXyX$XpXVX$XVXpX$XyXtXkXrXiXαX$XiXαXyXEX$XFX$XEXyXαXiX$XαXiXrXkXtXyX$XpXVX$XVXpX$XyXtXkXrXiXαX$XiXαXyXEX$XαXηXtXαX$XWXyX$XyXWX$XpXαXqXηX$XeXαXhX$XdX$XpX$XdX$XyXeXαX$XEXyXαXiX$XαXiXrXkXtXyX$XpXVX$XVXpX$XyXtXkXrXiXα…...

SLT简介【简单介绍SLT】
SLT简介 在c的学习当中STL的学习是一个很重要的一环,但是STL又是一个庞大的章节,因此这里我们先简单介绍一下STL,有助于后面我们对STL的学习,这里就是做一个简单的介绍,并无干货。 1.什么是STL STL(standard templa…...

vue实现pdf下载——html2canvas
html2canvas 官方文档https://html2canvas.hertzen.com/getting-started html2canvas 的原理是通过遍历DOM树,将每一个HTML元素转化为Canvas对象,并叠加到一起形成一张完整的图片或者PDF文件。 1. 安装插件 npm install html2canvas jspdf --save 2.使用(页面已经…...

安装docker+mysql的一些坑
yum -y install docker 提示missing signature 参考这里 https://www.8a.hk/news/content/8235.html 卸载旧的docker sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-engine 安装…...

React Native采集数据离线存储、网络状态监控、加密上传、鉴权
在无网络环境下进行数据采集并在有网络时上传至服务器,同时确保数据的鉴权和加密,这一需求需要考虑多方面的实现细节。无论您选择原生开发还是使用React Native(甚至Expo),以下是如何实现这一需求的具体步骤和建议。 …...
网络数据库后端相关面试题(其三)
18, 传输控制协议tcp和用户数据报协议udp有哪些区别 第一,tcp是面向字节流的,基本的传输单位是tcp报文段;而udp是面向报文的,基本传输单位是用户数据报。 第二, tcp注重安全可靠性,连接双方在…...

Hadoop之HDFS分布式文件系统
HDFS简介 Hadoop Distributed File System (HDFS): HDFS 是 Hadoop 的分布式文件系统,它设计用于存储大量数据,并提供 高吞吐率的数据访问,通过将数据分块存储在多个节点上,实现数据的冗余存储和容错。 HDFS重要概念 HDFS 通过统一的命名空间目录树来定位文件; 另外,它…...
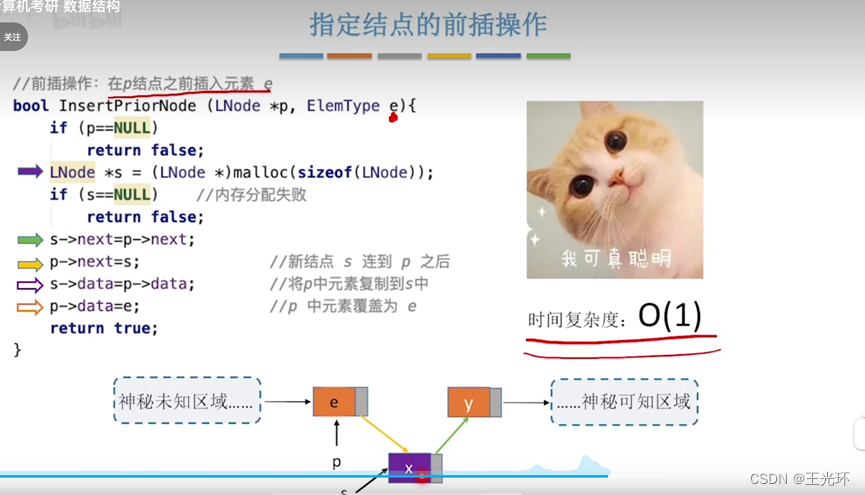
插入删除单链表指定结点-偷天换日法
王道说下面的代码有BUG,比如当删除的结点p在最后一个元素时,p->nextNULL; So *q NULL; q->data就是错误的,我认为加个判断就行 加个判断即可 /*看着是删除q了,从结果上看就是把p删除了 偷天换日法*/ bool DeleteNode(LNod…...

MybatisPlus代码生成器使用案例
针对数据库中的实体类表,自动生成相关的pojo类,mapper,service等 1. Get-Started 基于mybatisplus,idea下载mybatisplus插件 sql文件 /*!40101 SET OLD_CHARACTER_SET_CLIENTCHARACTER_SET_CLIENT */; /*!40101 SET NAMES utf8 …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
