在CSS中,可以使用 float 属性来设置元素浮动
在CSS中,可以使用float属性来设置元素浮动。float属性有三个值:left、right和none。
float: left;:将元素浮动到左侧。float: right;:将元素浮动到右侧。float: none;:取消元素的浮动(默认值)。
以下是一个简单的示例,演示如何设置元素浮动:
HTML:
<div class="float-left">左侧浮动元素</div>
<div class="float-right">右侧浮动元素</div>
CSS:
.float-left {float: left;
}.float-right {float: right;
}
在这个示例中,我们为.float-left类设置了float: left;,使其浮动到左侧,为.float-right类设置了float: right;,使其浮动到右侧。
相关文章:

在CSS中,可以使用 float 属性来设置元素浮动
在CSS中,可以使用float属性来设置元素浮动。float属性有三个值:left、right和none。 float: left;:将元素浮动到左侧。float: right;:将元素浮动到右侧。float: none;:取消元素的浮动(默认值)。…...
wordpress主题开发
科普一:wordpress 是一套用 php 这个语言写的CMS后台管理系统,即我们大家的 wordpress 网站后台是一样的,能体现我们网站外观不同的地方就在于wordpress主题(即皮肤),而这个主题的基本构成是 htmlcssjavasc…...
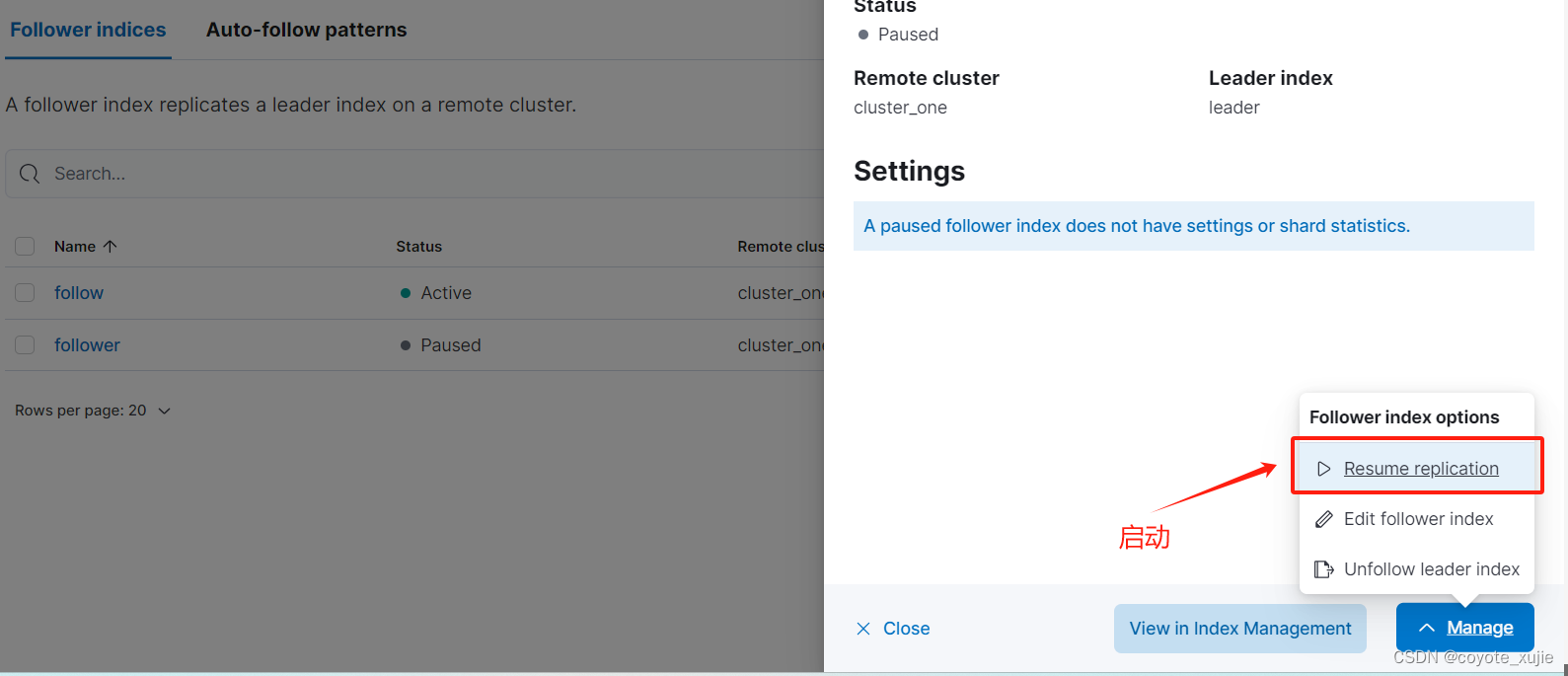
Elasticsearch 认证模拟题 - 17
这两道题目非常具有代表性,分别是跨集群复制和跨集群检索,需要相应的 许可 这里在虚拟机上搭建集群完成这两道题目,这里补充一下 elasticsearch 和 kibana 的配置文件 # elasticsearch.yml cluster.name: cluster2 node.name: cluster2-node…...

Swift 中更现代化的调试日志系统趣谈(一)
概述 昨天凌晨苹果刚刚发布了 WWDC2024 一系列新视频,这标志着苹果开发的一只脚已迈入人工智能(Apple Intelligence)的崭新时代。即便如此,我相信不少秃头码农们还在使用一些“远古简陋”的调试方法来剖析 2142 年的代码。 不过别担心,这一切将在小伙伴们学完本系列博文后…...

深入理解Java中的SPI机制
1. 简介 SPI(Service Provider Interface) 是Java提供的一种为服务框架提供服务实现的机制。它允许框架在运行时动态地发现服务的实现,从而实现模块化设计。在Java中,SPI机制主要用于解耦API和实现,使得应用程序可以在…...

2、python 基础学习总结
文章目录 一、python 标识符和变量命名规则1、python 标识符2 python 变量和变量命名规则 二、数据类型2.1 Numbers(数字类型)2.2 String(字符串类型)2.2.1 单引号、双引号、三引号字符串之间的区别2.2.2 转义字符 在这里插入图片…...

线程的状态!!!
NEW:(初始状态) 线程对象已经创建,但尚未启动。此时,线程还没有开始执行。 RUNNABLE:(运行状态) 线程已经启动并且正在运行,或者准备好运行,但可能由于其他线…...
是什么?如何解决?)
Hsah碰撞(冲突)是什么?如何解决?
Hash冲突:两个不同的对象经过hash计算后得到的hash值相同,导致冲突。 解决方法: 1、开放地址法:在哈希表中寻找其他的空闲位置来存储冲突的元素。 2、拉链法:拉链法的基本思路是在每个哈希槽中存储一个链表。当发生…...

doc 和 docx 文件的区别
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...
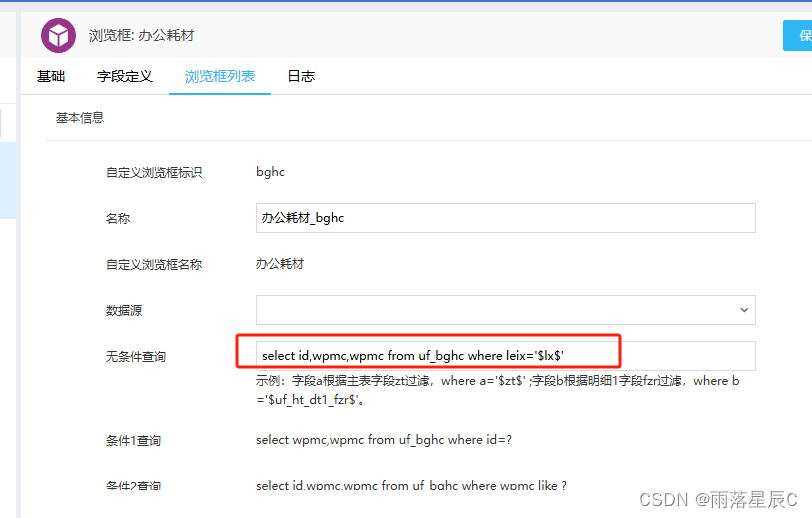
泛微OA E9 浏览框显示的数据根据表单字段过滤
一、实现效果:如图所示,字段“物品名称”浏览框显示的数据根据“类型”字段进行过滤。 二、实现方法: 1、建模引擎-应用建模-浏览框-浏览框列表中单击“办公耗材”-“浏览框列表”-“操作”-“编辑” 2、sql语句中根据OA自带是示例增加where…...
)
AIGC涉及到的算法(一)
目录 1. 生成对抗网络(GAN) 2. 变分自编码器(VAE) 3. 扩散模型(Diffusion Model) 4. Transformer 模型 5. 自然语言处理算法(NLP) 6. 计算机视觉算法(CV) 7. 神经网络算法 8. 决策树算法 9. 遗传算法 10. 聚类算法 1. 生成对抗网络(GAN) 原理与应用:生成对…...

一种基于单片机的智能饮水机设计
随着人们生活水平的提高,对美好生活质量的追求也越来越高。饮 水机是人们日常生活不可或缺的,实现饮水机的智能化控制不但方便, 而且更加安全。本文提出一种基于单片机的智能饮水控制系统,通过传 感器实现对水温的监测,…...
)
竞争性谈判和竞争性磋商的区别(电子化招采系统)
竞争性谈判和竞争性磋商在政府采购和项目采购中都是常用的方式,但它们在多个方面存在显著的区别,郑州信源数智化招采系统可满足各种招标和采购方式,结合多年招采系统研发和实施经验,对竞争性谈判和竞争性磋商的区别总结如下: 1、…...
STM32F413 STM32F423数据手册 中文版 STM32F413 STM32F423勘误手册英文版等文档
链接: https://pan.baidu.com/s/1AeYaoFb5Wurii6OM2ZlY2Q 提取码: a3tj 本文分享关于STM32F413 和STM32F423芯片的相关资料,主要资源如下图所示: 包含的文档有: STM32F40xxx and STM32F41xxx单片机编程手册 中文版 英文版 STM32F413xG 423…...
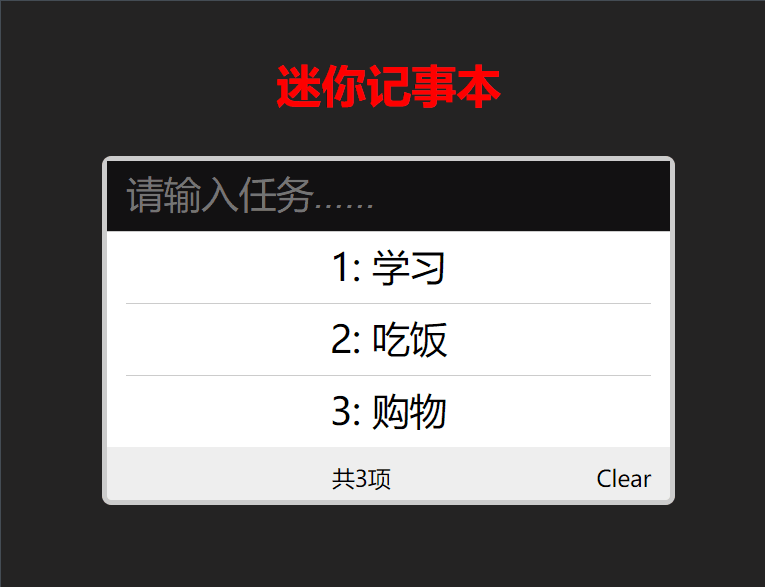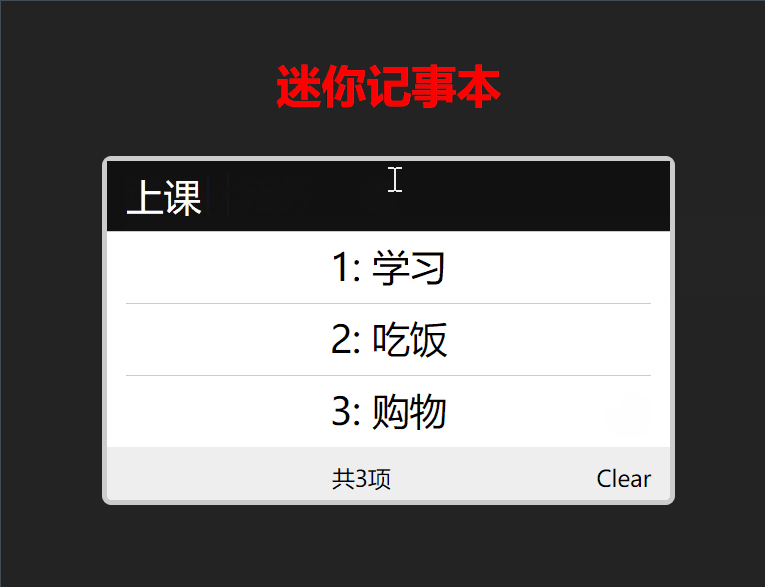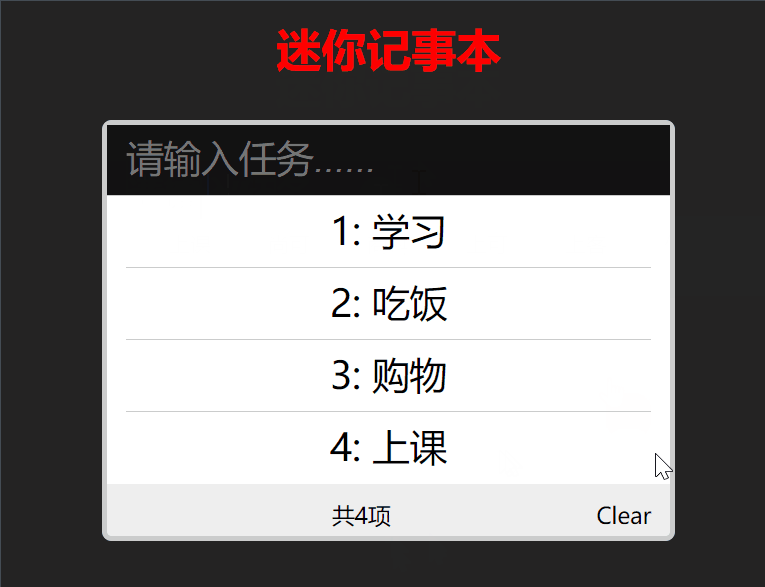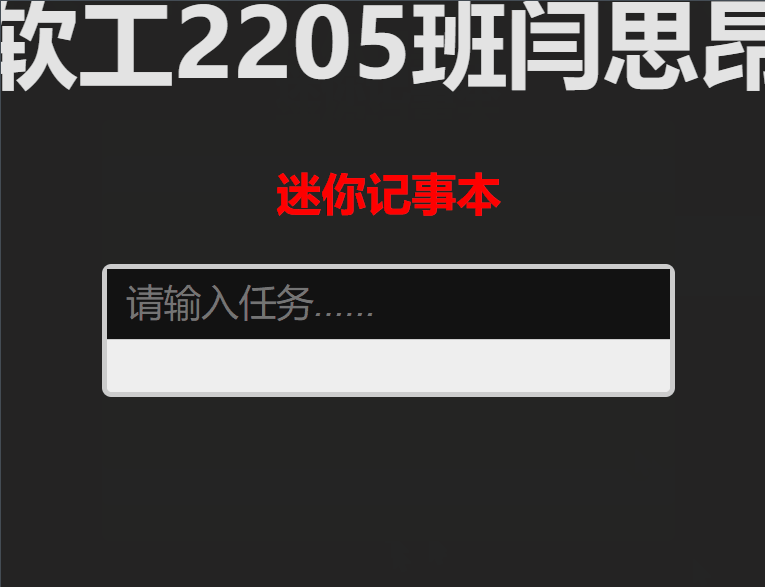
【Vue】——前端框架的基本使用
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

tmux-以脚本中的tmux命令为例解释常用tmux命令
SESSIONenv_monitor_hr_parking ----- 将会话名称env_monitor_hr_parking赋值给变量SESSION tmux new-session -s $SESSION -n runner -d ----- new-session 用于创建新的会话。-s $SESSION 是一个选项,其中 $SESSION 是你想要给你的新会话命名的名称。-n runner 是…...

计算机网络 —— 数据链路层(以太网)
计算机网络 —— 数据链路层(以太网) 什么是以太网以太网传输介质和拓扑结构的发展传输介质的发展:拓扑结构的发展: 10BASE-T 以太网适配器和MAC地址适配器(Adapter)MAC地址适配器与MAC地址的关系 MAC帧以太…...

记录 unplugin-vue-components不生效
之前用 vite VUE3 TS 开发了几个项目,最近因为一个新项目,想着升级这些版本,就重新起了一个项目,结果遇到了然自己爆炸的问题。 element-plus 官方推荐的按需引入,配置也给的明明白白: npm install -D …...
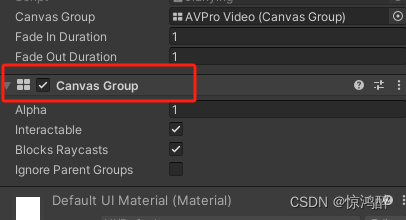
⭐Unity 控制任意UI的渐隐渐显
使用脚本之前先给要控制的UI加上CanvasGroup组件 解释: 这个脚本使用协程来逐渐改变CanvasGroup的alpha值,从而实现渐隐和渐显的效果。 Mathf.Lerp函数用于在指定的时间内平滑地从当前透明度过渡到目标透明度。 通过调用FadeIn和FadeOut方法,你可以在任…...

web移动前端网页:深度剖析与未来展望
web移动前端网页:深度剖析与未来展望 在数字化浪潮席卷全球的今天,web移动前端网页作为连接用户与数字世界的桥梁,其重要性不言而喻。本文将从四个方面、五个方面、六个方面和七个方面,对web移动前端网页进行深入的剖析和展望&am…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
