36、matlab矩阵特征值、特征向量和奇异值
1、名词说明
1)特征值
特征值(Eigenvalues)是矩阵的一个重要概念,在线性代数中起着非常重要的作用。给定一个n×n的方阵A,如果存在一个非零向量v,使得矩阵A作用于向量v后,得到的结果与向量v成比例(即Av=λv,其中λ为标量),那么λ就是矩阵A的特征值,v就是对应于特征值λ的特征向量。
特征值和特征向量的概念与矩阵的对角化有密切的关系。通过特征值和特征向量的求解,可以将矩阵对角化为对角矩阵,简化矩阵的计算和分析。特征值和特征向量还在矩阵的谱理论和矩阵的性质研究中扮演着重要的角色。
一些常见的特征值相关的问题包括:求解特征值和特征向量、特征值的性质(如重数、特征多项式等)、特征值的影响(如对角化、矩阵的稳定性分析等)等。
2)广义特征值
在线性代数中,矩阵的广义特征值(Generalized Eigenvalues)是指两个矩阵的特征值。给定两个n×n的矩阵A 和 B,广义特征值λ是一个非零的标量λ,使得存在一个非零的n 维向量x,使得如下广义特征方程成立:
Ax = λBx
其中A 和 B 是给定的矩阵,x 是非零向量。广义特征值问题是通过求解上述方程来获取特征值λ和相应的特征向量x 的过程。
3)特征向量
特征向量(Eigenvectors)是与特征值(Eigenvalues)相关联的一组向量。对于一个给定的方阵A,如果存在一个非零向量v,使得矩阵A作用于向量v后,得到的结果与向量v成比例(即Av=λv,其中λ为标量),那么v就是矩阵A的特征向量,对应的标量λ为特征值。
特征向量在许多领域中都有着广泛的应用。在线性代数中,特征向量可以帮助我们理解矩阵的性质和对角化。通过求解特征值和特征向量,我们可以将矩阵对角化,简化矩阵的计算和分析过程。
4)奇异值
奇异值(Singular Values)是线性代数中一个非常重要的概念,特别在矩阵分解和降维技术中扮演着关键的角色。对于一个任意的矩阵A(不一定是方阵),其奇异值分解(Singular Value Decomposition,SVD)可以表示为:
A = UΣV^T
其中,U和V都是正交矩阵,Σ是一个对角矩阵,对角线上的元素称为矩阵A的奇异值。通常情况下,奇异值按照非增的次序排列。奇异值分解不仅能够将矩阵A分解为一系列特征较强的奇异向量,还为矩阵的低秩近似提供了有效的方式。
5)正交矩阵
正交矩阵是指在实数域或复数域上的一个方阵,满足其转置矩阵与逆矩阵相等的性质。换句话说,一个正交矩阵A满足以下条件:A^T * A = A * A^T = I,其中I为单位矩阵。
2、eig ():特征值和特征向量求解
1)语法
语法:e = eig(A) 返回一个列向量,其中包含方阵 A 的特征值。
语法:[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V,其列是对应的右特征向量,使得 A*V = V*D。
语法:[V,D,W] = eig(A) 还返回满矩阵 W,其列是对应的左特征向量,使得 W'*A = D*W'。
语法:e = eig(A,B) 返回一个列向量,其中包含方阵 A 和 B 的广义特征值。
语法:[V,D,W] = eig(A,B) 还返回满矩阵 W,其列是对应的左特征向量,使得 W'*A = D*W'*B。
[___] = eig(___,outputForm) 支持上述语法中的任何输入或输出参量,并以 outputForm 指定
的形式返回特征值。将 outputForm 指定为 "vector" 可返回列向量中的特征值,指定为 "matrix"
可返回对角矩阵中的特征值。
2)参数
A — 输入矩阵 B — 广义特征值问题输入矩阵 outputForm — 特征值的输出格式
e — 特征值(以向量的形式返回) V — 右特征向量 D — 特征值(以矩阵的形式返回)
W — 左特征向量
3)矩阵特征值
代码及运算
A = gallery("lehmer",4)%创建对称正定矩阵
e = eig(A)%特征值计算
D = eig(A,"matrix")%对角矩阵显示特征值A =1.0000 0.5000 0.3333 0.25000.5000 1.0000 0.6667 0.50000.3333 0.6667 1.0000 0.75000.2500 0.5000 0.7500 1.0000e =0.20780.40780.84822.5362D =0.2078 0 0 00 0.4078 0 00 0 0.8482 00 0 0 2.53624) 矩阵的特征值和特征向量
代码及运算
A = gallery("lehmer",4)%创建对称正定矩阵
[V,D] = eig(A)%D为特征值的对角矩阵
A*V - V*D%验证A =1.0000 0.5000 0.3333 0.25000.5000 1.0000 0.6667 0.50000.3333 0.6667 1.0000 0.75000.2500 0.5000 0.7500 1.0000V =0.0693 -0.4422 -0.8105 0.3778-0.3618 0.7420 -0.1877 0.53220.7694 0.0486 0.3010 0.5614-0.5219 -0.5014 0.4662 0.5088D =0.2078 0 0 00 0.4078 0 00 0 0.8482 00 0 0 2.5362ans =1.0e-14 *-0.0309 0.0028 0.0222 -0.0222-0.0319 0.0111 -0.0083 -0.0444-0.0833 -0.0208 0.0278 -0.1332-0.0056 0 0 0.04445) 左特征向量
代码及运算
A = gallery("lehmer",4)%创建对称正定矩阵
[V,D,W] = eig(A)
W'*A - D*W'%验证A =1.0000 0.5000 0.3333 0.25000.5000 1.0000 0.6667 0.50000.3333 0.6667 1.0000 0.75000.2500 0.5000 0.7500 1.0000V =0.0693 -0.4422 -0.8105 0.3778-0.3618 0.7420 -0.1877 0.53220.7694 0.0486 0.3010 0.5614-0.5219 -0.5014 0.4662 0.5088D =0.2078 0 0 00 0.4078 0 00 0 0.8482 00 0 0 2.5362W =0.0693 -0.4422 -0.8105 0.3778-0.3618 0.7420 -0.1877 0.53220.7694 0.0486 0.3010 0.5614-0.5219 -0.5014 0.4662 0.5088ans =1.0e-14 *-0.0309 -0.0319 -0.0833 -0.00560.0028 0.0111 -0.0208 00.0222 -0.0083 0.0278 0-0.0222 -0.0444 -0.1332 0.04446) 广义特征值
代码及运算
A = [1/sqrt(2) 0; 0 1]
B = [0 1; -1/sqrt(2) 0]
[V,D]=eig(A,B)
A*V - B*V*D%验证A =0.7071 00 1.0000B =0 1.0000-0.7071 0V =1.0000 + 0.0000i 1.0000 + 0.0000i0.0000 - 0.7071i 0.0000 + 0.7071iD =0.0000 + 1.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 - 1.0000ians =0 00 03、svd()奇异值分解
1)语法
语法:S = svd(A) 以降序顺序返回矩阵 A 的奇异值。
语法:[U,S,V] = svd(A) 执行矩阵 A 的奇异值分解,因此 A = U*S*V'。
[___] = svd(___,outputForm) 还可以指定奇异值的输出格式。您可以将此选项与上述任一输入或输出参量组合一起使用。指定 "vector" 以列向量形式返回奇异值,或指定 "matrix" 以对角矩阵形式返回奇异值。
2)参数
A :输入矩阵 outputForm :奇异值的输出格式
U :左奇异向量 S :奇异值 V :右奇异向量
3)矩阵的奇异值
代码及运算
A = [1 0 1; -1 -2 0; 0 1 -1]%满秩矩阵
s = svd(A)A =1 0 1-1 -2 00 1 -1s =2.46051.69960.23914) 奇异值分解
代码及运算
A = [1 2; 3 4; 5 6; 7 8]
[U,S,V] = svd(A)
U*S*V'A =1 23 45 67 8U =-0.1525 -0.8226 -0.3945 -0.3800-0.3499 -0.4214 0.2428 0.8007-0.5474 -0.0201 0.6979 -0.4614-0.7448 0.3812 -0.5462 0.0407S =14.2691 00 0.62680 00 0V =-0.6414 0.7672-0.7672 -0.6414ans =1.0000 2.00003.0000 4.00005.0000 6.00007.0000 8.0000相关文章:

36、matlab矩阵特征值、特征向量和奇异值
1、名词说明 1)特征值 特征值(Eigenvalues)是矩阵的一个重要概念,在线性代数中起着非常重要的作用。给定一个nn的方阵A,如果存在一个非零向量v,使得矩阵A作用于向量v后,得到的结果与向量v成比例ÿ…...
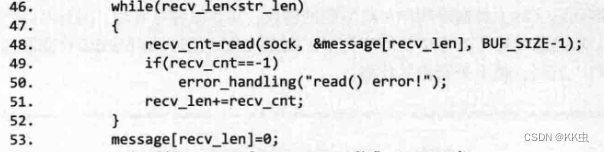
【网络编程】基于TCP的服务器端/客户端
TCP是Transmission Control Protocol(传输控制协议)简写。因为TCP套接字是面向连接的,因此又称为基于流的套接字。 把协议分为多个层次,设计更容易,通过标准化操作设计开放式系统 网络层介绍 链路层 链路层是物理连接领域标准化的结果&…...

企业中的绩效管理
背景 企业中为何需要绩效管理,企业绩效管理为何比较难,这在企业管理中是非常难,同样也是非常有价值的命题,那么首先应该对这个命题有清晰的认知,特别是要想明白为何企业需要绩效管理,应该先明白企业。 企…...
C++面试八股文:static和const的关键字有哪些用法?
100编程书屋_孔夫子旧书网 某日二师兄参加XXX科技公司的C工程师开发岗位第7面: 面试官:C中,static和const的关键字有哪些用法? 二师兄:satic关键字主要用在以下三个方面:1.用在全局作用域,修饰的变量或者…...

Qt飞机大战小游戏
Gitee地址 :plane-game: 基于Qt的飞机大战小游戏 GitHub地址: https://github.com/a-mo-xi-wei/plane-game...

Flarum 安装和使用教程
随着开源社区的日益繁荣,人们对社区品质的要求也越来越高。传统的 BBS 论坛模式已经难以满足现代用户对美观、便捷、互动性的需求。搭建一个现代化的高品质社区,成为许多网站管理者的迫切需求和共同挑战。 今天就给大家安利一款现代化的、优雅的开源论坛…...

Java老人护理上门服务类型系统小程序APP源码
🌸 老人上门护理服务系统:温暖与专业并存 🌸 一、🏠 走进老人上门护理服务系统 随着社会的快速发展,我们越来越关注老年人的生活质量。老人上门护理服务系统应运而生,它结合了现代科技与人性化服务&#…...

Spring Boot整合Knife4j-3.0.3
文章目录 Spring Boot整合Knife4j-3.0.31. 引言2. 快捷的解决方案2.1 修改knife4j的依赖2.2 application.yml增加配置3.3 SwaggerConfig配置如下 Spring Boot整合Knife4j-3.0.3 1. 引言 前面我写过一篇关于整合knife4j的文档 Spring Boot整合Knife4j-2.0.7 最近我引入redissi…...

使用R语言生成CDISC SDTM.AE domain
写在前面 - 使用的是Rstudio - 其实R已经有生成sdtm相关的package,以下代码仅作为练习R语言的语法,不是高效生成sdtm的方法 - 代码中没有解决的问题包括:EPOCH相关的逻辑没有考虑partial date的情况;在使用arrange() function做…...

怎么防止源代码泄露?9种方法教会你!
怎么防止源代码泄露?首先要了解员工可以通过哪些方式将源代码传输出去! 物理方法: — 网线直连,即把网线从墙上插头拔下来,然后和一个非受控电脑直连; — winPE启动,通过光盘或U盘的winPE启动,甚…...

原生JS如何实现可配置DM码
原生JS如何实现可配置DM码 一、 DM码简介 1、 Data Matrix码 Data Matrix码是一种二维条形码,简称DM码,由美国公司International Data Matrix, Inc.(I.D. Matrix)在1994年发明,Data Matrix码中的行数和列数随二维码中存储的信息量而增加,信息限值是2335个字母数字字符…...

【Python】Python开发面试题库:综合考察面试者能力
文章目录 Python开发面试题库:综合考察面试者能力1. 基础语法与数据类型问题1:变量与数据类型问题2:列表与字典操作问题3:字符串操作问题4:元组解包问题5:集合操作问题6:基本运算问题7ÿ…...
大语言模型的sft
https://zhuanlan.zhihu.com/p/692892489https://zhuanlan.zhihu.com/p/692892489https://zhuanlan.zhihu.com/p/679450872https://zhuanlan.zhihu.com/p/6794508721.常...
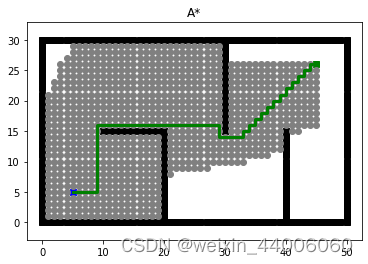
Astar路径规划算法复现-python实现
# -*- coding: utf-8 -*- """ Created on Fri May 24 09:04:23 2024"""import os import sys import math import heapq import matplotlib.pyplot as plt import time 传统A*算法 class Astar:AStar set the cost heuristics as the priorityA…...

低-零功率技术在军事中的应用
“低-零功率”概念最先由美国国防部提出,主要是针对诸如俄罗斯等大国的远程传感器,帮助美军破除“灰色地带挑衅”的威胁。由于“灰色地带”冲突仅依托小规模军事力量,其强度维持在不足以引发美国及其盟国进行直接干预的程度,因此&…...

【培训】企业档案管理专题(私货)
导读:通过该专题培训,可以系统了解企业档案管理是什么、为什么、怎么做。尤其是对档案的价值认知,如何构建与新质生产力发展相适应的企业档案工作体系将有力支撑企业新质生产力的发展,为企业高质量发展贡献档案力量,提…...
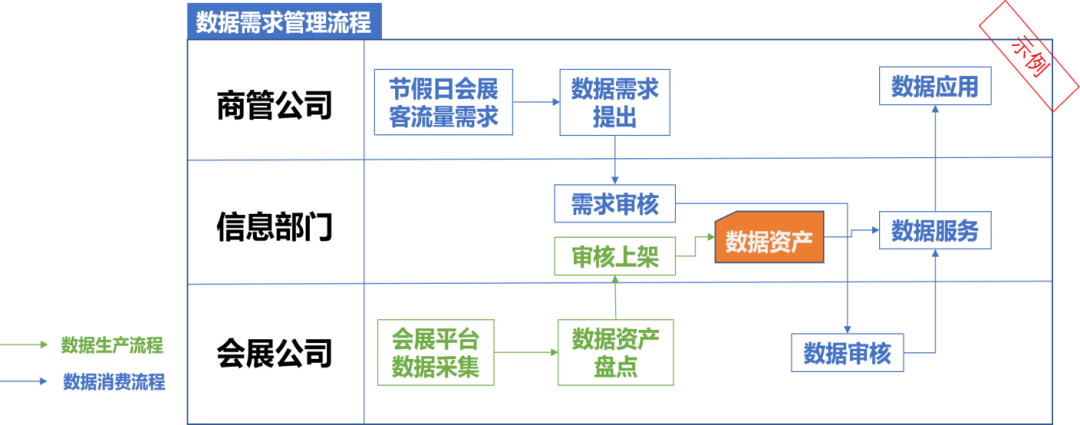
某国资集团数据治理落地,点燃高质量发展“数字引擎”
某国有资产经营控股集团为快速提升集团的内控管理能力和业务经营能力,以数字化促进企业转型的信息化建设势在必行。集团携手亿信华辰开启数据治理项目,在数据方面成功解决“哪里来、怎么盘、怎么管、怎么用”的问题,不断推动企业数字化转型…...
【AI测试版】)
2024.06.12【读书笔记】丨生物信息学与功能基因组学(第十四章 细菌和古细菌基因组 第二部分)【AI测试版】
读书笔记:《生物信息学与功能基因组学》第十四章 - 第二部分 摘要 第二部分深入讨论了基于不同标准的细菌和古细菌的分类方法,包括形态学、基因组大小和排列、生活方式以及与人类疾病的关系。此外,还探讨了基于核糖体RNA序列的分类方法&…...

企业数据API接口大全
一、工商信息 (1)精确获取企业唯一标识 根据企业名称、注册号或统一社会信用代码,获取企业唯一标识 (2)企业模糊查询 关键字名称模糊搜索匹配企业 (3)企业详情 根据企业唯一标识、企业名称…...

【HTML】格式化文本 pre 标签
文章目录 <pre> 元素中的文本以等宽字体显示,文本保留空格和换行符。 <pre> 元素支持 HTML 中的全局属性和事件属性。 示例: <pre> pre 元素中的文本 以等宽字体显示, 并且同时保留 空格 和 换行符。 </pre&…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
