【数据结构(邓俊辉)学习笔记】图06——最小支撑树
文章目录
- 0. 概述
- 1. 支撑树
- 2. 最小支撑树
- 3. 歧义性
- 4. 蛮力算法
- 5. Prim算法
- 5.1 割与极短跨越边
- 5.2 贪心迭代
- 5.3 实例
- 5.4 实现
- 5.5 复杂度
0. 概述
学习下最小支撑树和prim算法。
1. 支撑树
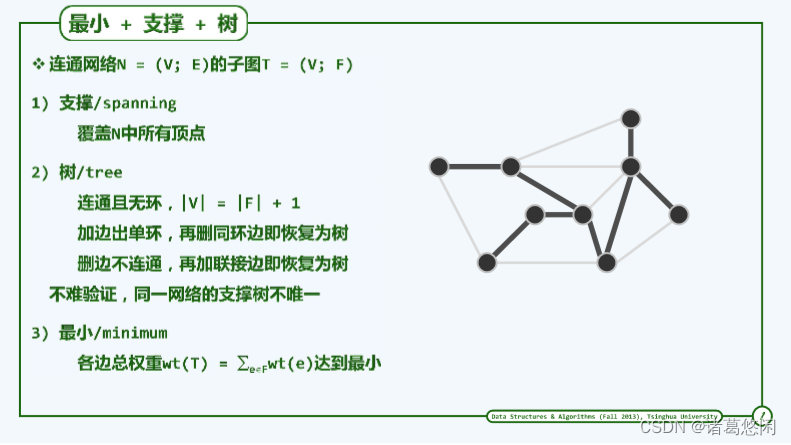
最小的连通图是树。
连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称作G的一棵支撑树或生成树(spanning tree)。
就保留原图中边的数目而言,支撑树既是“禁止环路”前提下的极大子图,也是“保持连通”前提下的最小子图。
确切地,尽管同一幅图可能有多棵支撑树,但由于其中的顶点总数均为n,故其采用的边数也均为n - 1。
2. 最小支撑树
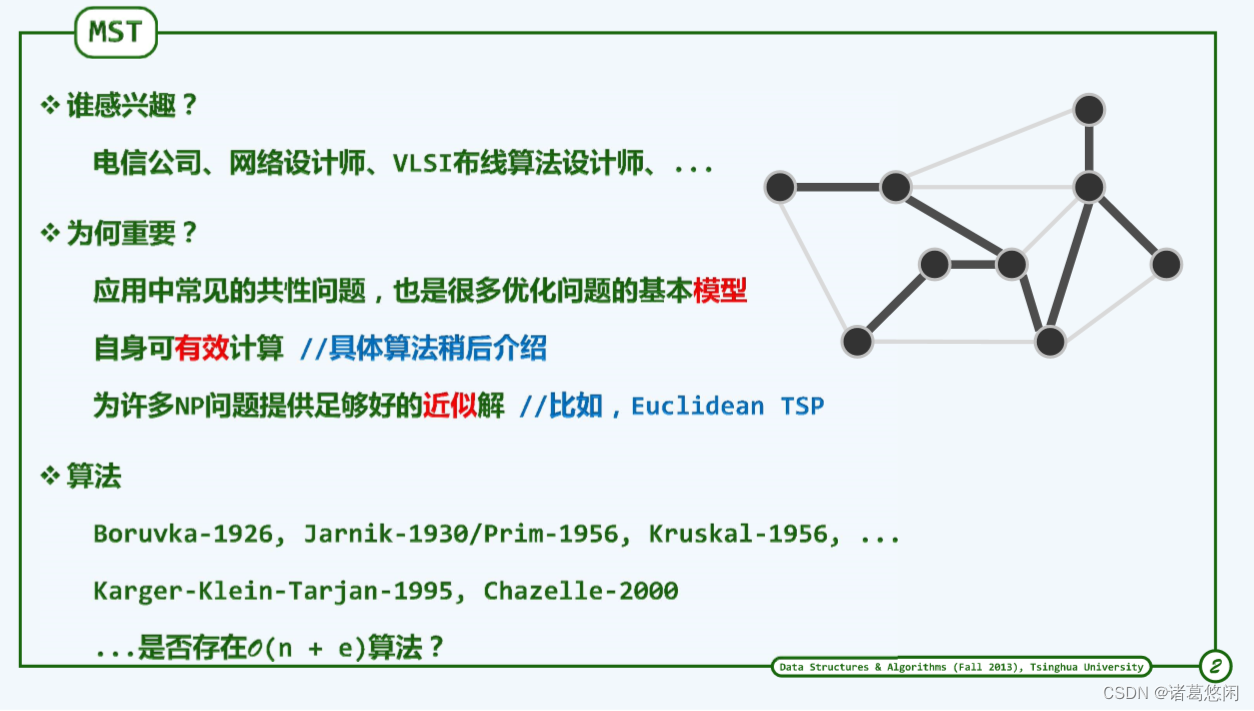
若图G为一带权网络,则每一棵支撑树的成本(cost)即为其所采用各边权重的总和。在G的所有支撑树中,成本最低者称作最小支撑树(minimum spanning tree, MST)。
3. 歧义性
尽管同一带权网络通常都有多棵支撑树,但总数毕竟有限,故必有最低的总体成本。然而,总体成本最低的支撑树却未必唯一。
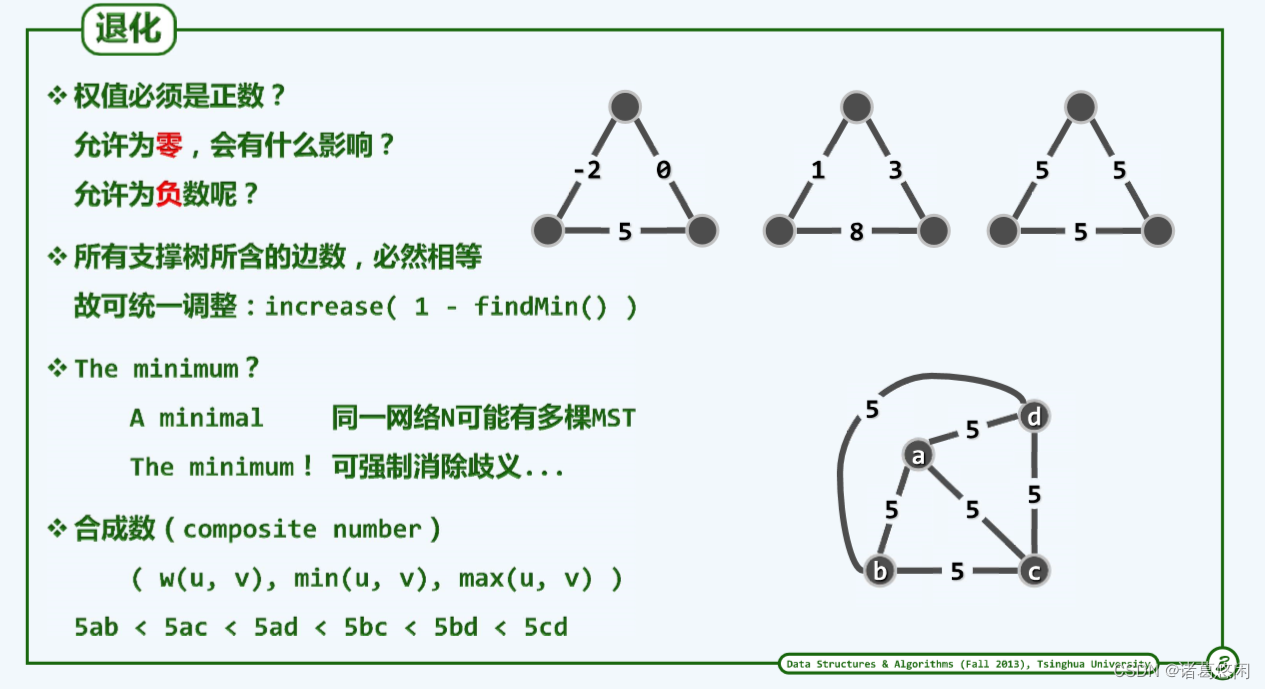
最小支撑树允许有负数,因为它算的是total cast。
若有重边,通过强制附加某种次序即可消除这种歧义性。
4. 蛮力算法
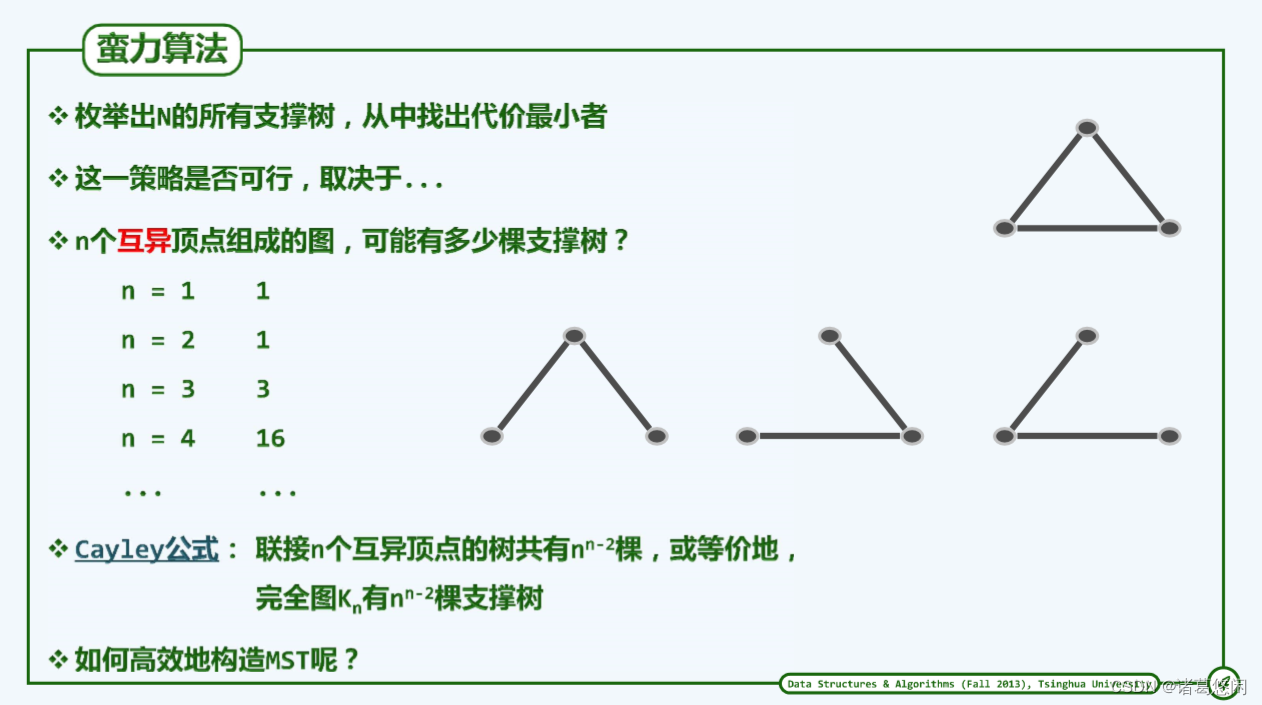
由最小支撑树的定义,可直接导出蛮力算法大致如下:逐一考查G的所有支撑树并统计其成本,从而挑选出其中的最低者。然而根据Cayley公式,由n个互异顶点组成的完全图共有 n n − 2 n^{n-2} nn−2棵支撑树,即便忽略掉构造所有支撑树所需的成本,仅为更新最低成本的记录就需要O( n n − 2 n^{n-2} nn−2)时间。
事实上基于PFS搜索框架,并采用适当的顶点优先级更新策略,即可得出如下高效的最小支撑树构造算法。
5. Prim算法
5.1 割与极短跨越边
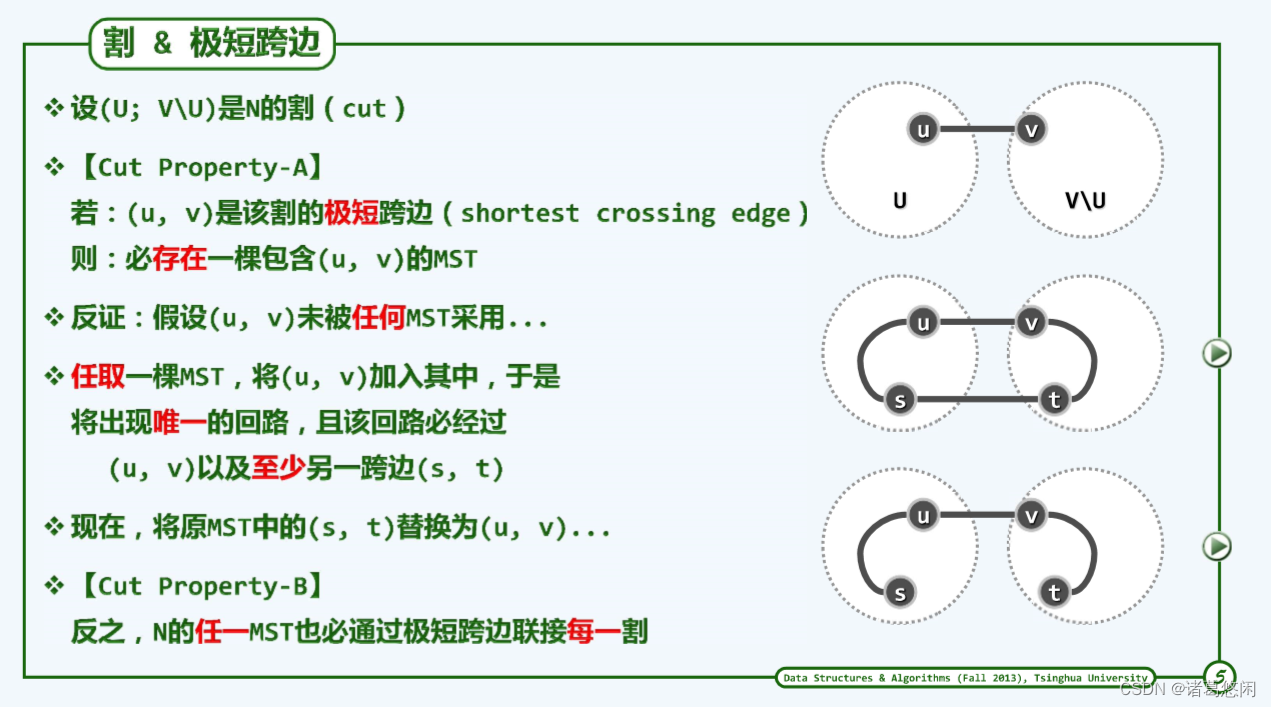
图G = (V; E)中,顶点集V的任一非平凡子集U及其补集V\U都构成G的一个割(cut),记作(U : V\U)。若边uv满足u∈U且v∈V\U,则称作该割的一条跨越边(crossing edge)。因此类边联接于V及其补集之间,故亦形象地称作该割的一座桥(bridge)。
Prim算法的正确性基于以下事实:最小支撑树总是会采用联接每一割的最短跨越边。
5.2 贪心迭代
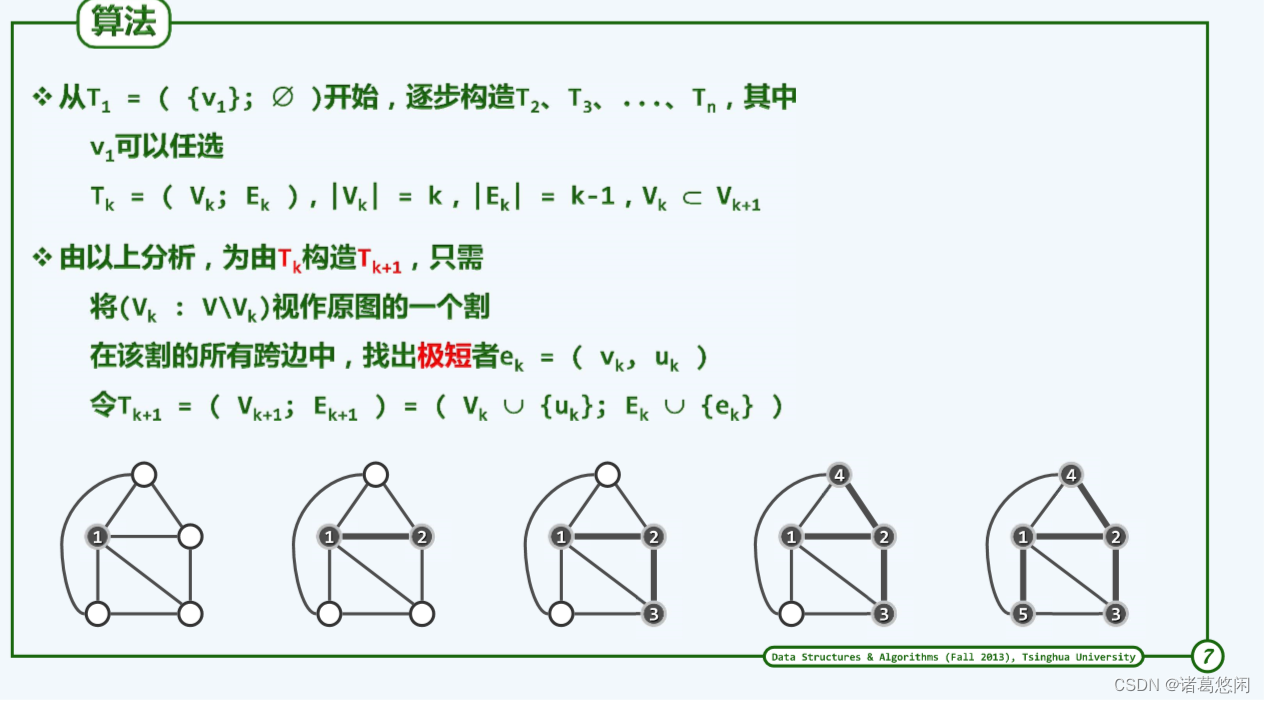
5.3 实例
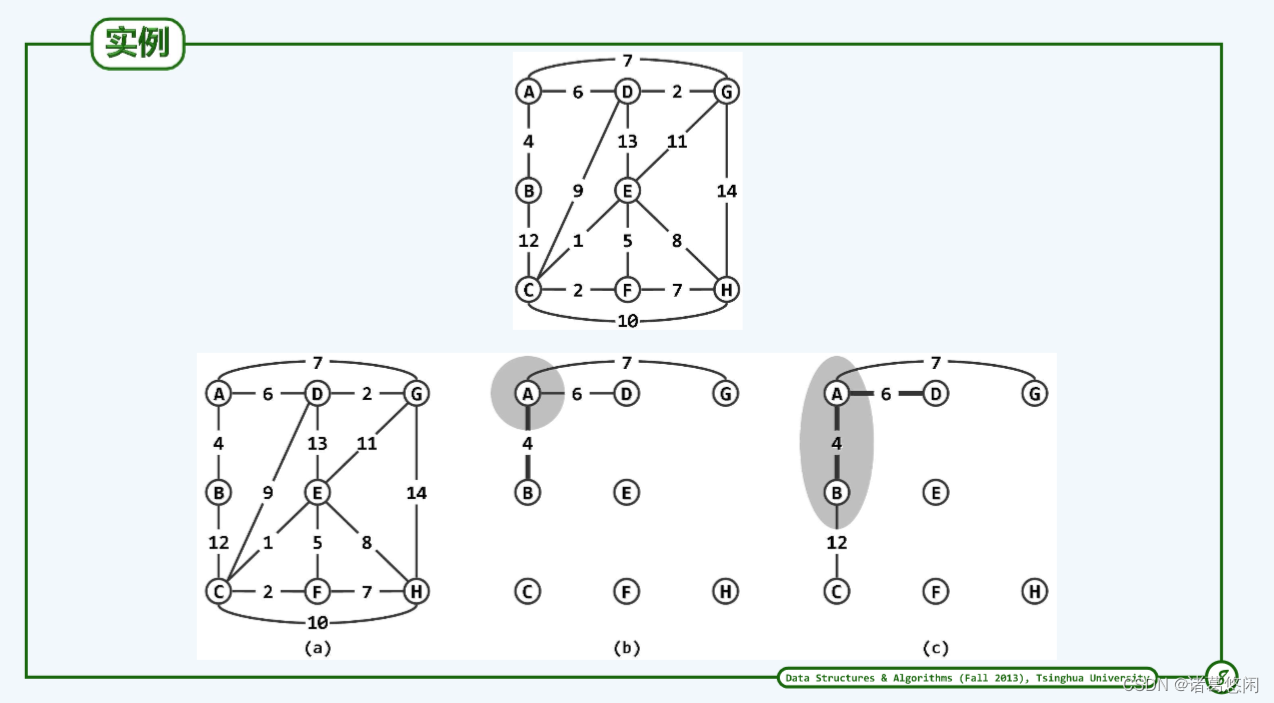
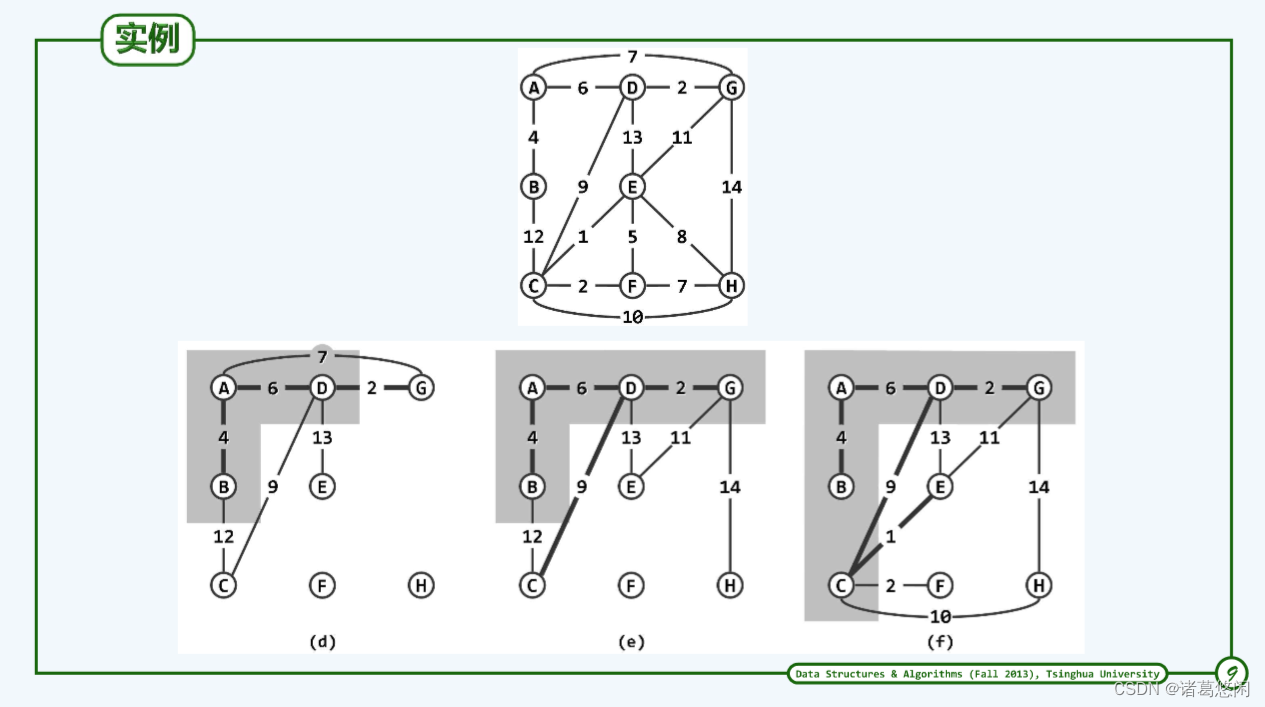
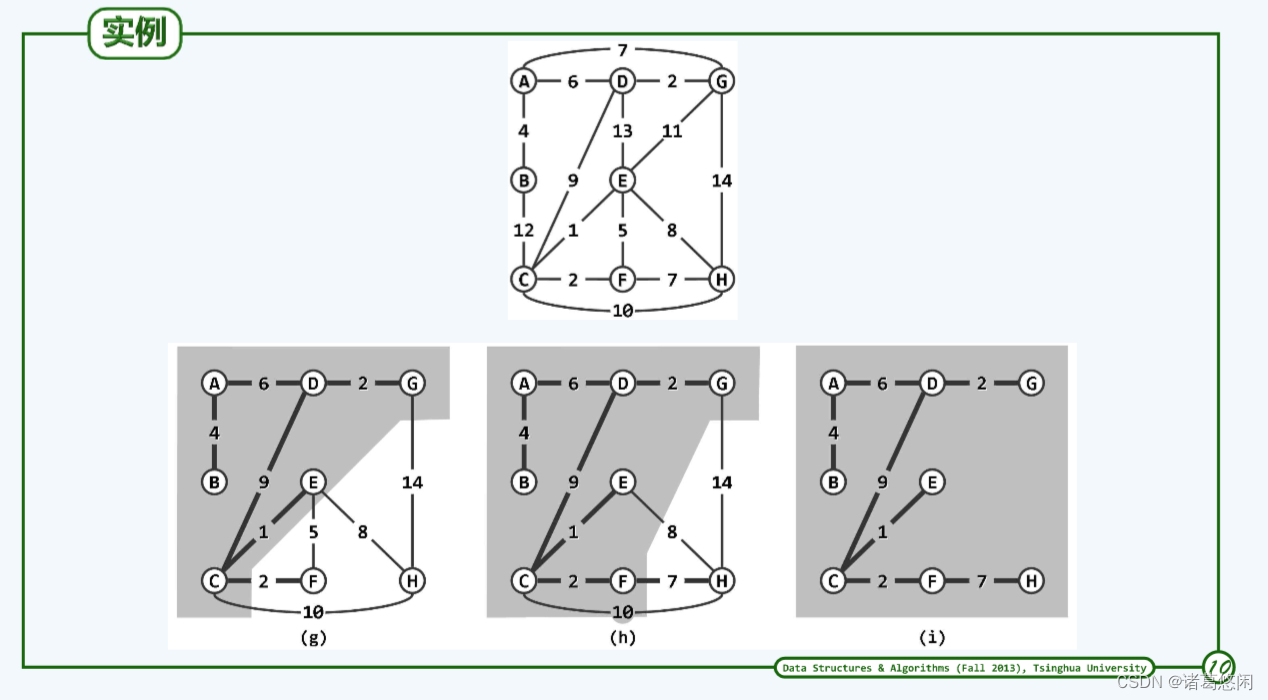
5.4 实现
这个实现无非就是一个PFS。

这棵子树上的点认为都访问过了,没有访问的点(补集上的点)手上都拥有一个优先级数,这个数就是代表它到子树的距离,这个距离在任何时刻各自都会实现于某个特定的点,每次要做的事就是在树中找到最小的把它拓展进来,接下来再update。

接下来就是为prim算法写一个优先级更新器,实现更新算法。实现流程:
在当前图g中,如果有一个点uk刚刚被扩展进来,加入到这棵树中,对于它的每个尚未被发现的邻居v,按照prim策略做松弛。首先判断下当前的提供的优先级数是否更好,如果当前的优先级数更好便会欣然接受这个。再更新下v的父亲。
5.5 复杂度
目前只是把算法将明白了,数据结构还差的很远,每次查找优先级数还比较慢,以上Prim算法的时间复杂度为O( n 2 n^2 n2)。作为PFS搜索的特例,Prim算法的效率也可借助优先级队列进一步提高。
相关文章:

【数据结构(邓俊辉)学习笔记】图06——最小支撑树
文章目录 0. 概述1. 支撑树2. 最小支撑树3. 歧义性4. 蛮力算法5. Prim算法5.1 割与极短跨越边5.2 贪心迭代5.3 实例5.4 实现5.5 复杂度 0. 概述 学习下最小支撑树和prim算法。 1. 支撑树 最小的连通图是树。 连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称…...

海豚调度清理:使用 API 轻松清理历史工作流实例以及日志文件
💡 本系列文章是 DolphinScheduler 由浅入深的教程,涵盖搭建、二开迭代、核心原理解读、运维和管理等一系列内容。适用于想对 DolphinScheduler了解或想要加深理解的读者。 祝开卷有益。 大数据学习指南 大家好,我是小陶,DolphinS…...

python怎么显示行号
我们如果想让Python IDLE显示行号,我们可以通过扩展IDLE功能来做到。 1.我们需要下载一个LineNumber.py扩展。 2.我们打开Python安装目录,找到安装目录下的Lib\idlelib目录,复制LineNumber到这个目录。 3.然后启动扩展。 4.配置扩展的方式…...

pytorch中,load_state_dict和torch.load的区别?
在 PyTorch 中,load_state_dict 和 torch.load 是两个不同的函数,用于不同的目的。 torch.load: 用途: 从磁盘加载一个保存的对象。这个对象可以是一个模型的整个状态字典(包含模型参数)、优化器状态字典、甚至是任意其他 Python …...
)
ObjectARX打印当前图纸为PDF,无延迟(亲测有效)
CAD二次开发定制ObjectARX安装配置AutoCAD插件ZWCAD插件C++ //----------------------------------------------------------------------------- //----- acrxEntryPoint.cpp //----------------------------------------------------------------------------- #include &quo…...
 dim=1 dim=-1 dim=2)
torch.squeeze() dim=1 dim=-1 dim=2
对数据的维度进行压缩 使用方式:torch.squeeze(input, dimNone, outNone) 将输入张量形状中的1 去除并返回。 如果输入是形如(A1B1C1D),那么输出形状就为: (ABCD) import torch x torch.rand(2, 1, 1, 3, 1, 4) print(x) print(x.shape) …...

智慧环保一体化平台简介
据悉,环保问题日益受到人们的关注,智慧环保一体化平台作为解决环保问题的有力工具,正逐渐走进人们的视野。朗观视觉智慧环保一体化平台通过整合各类环保资源,实现环境数据的实时监测、分析与管理,为环境保护提供智能化…...
idea在空工程中添加新模块并测试的步骤
ServicesTest是空的工程,没有pom文件。现在需要在ServicesTest目录下添加新模块作为新的工程,目的是写一下别的技术功能。 原先目录结构,ServicesTest是空的工程,没有pom文件。下面的几个模块是新的工程,相互独立。 1.…...
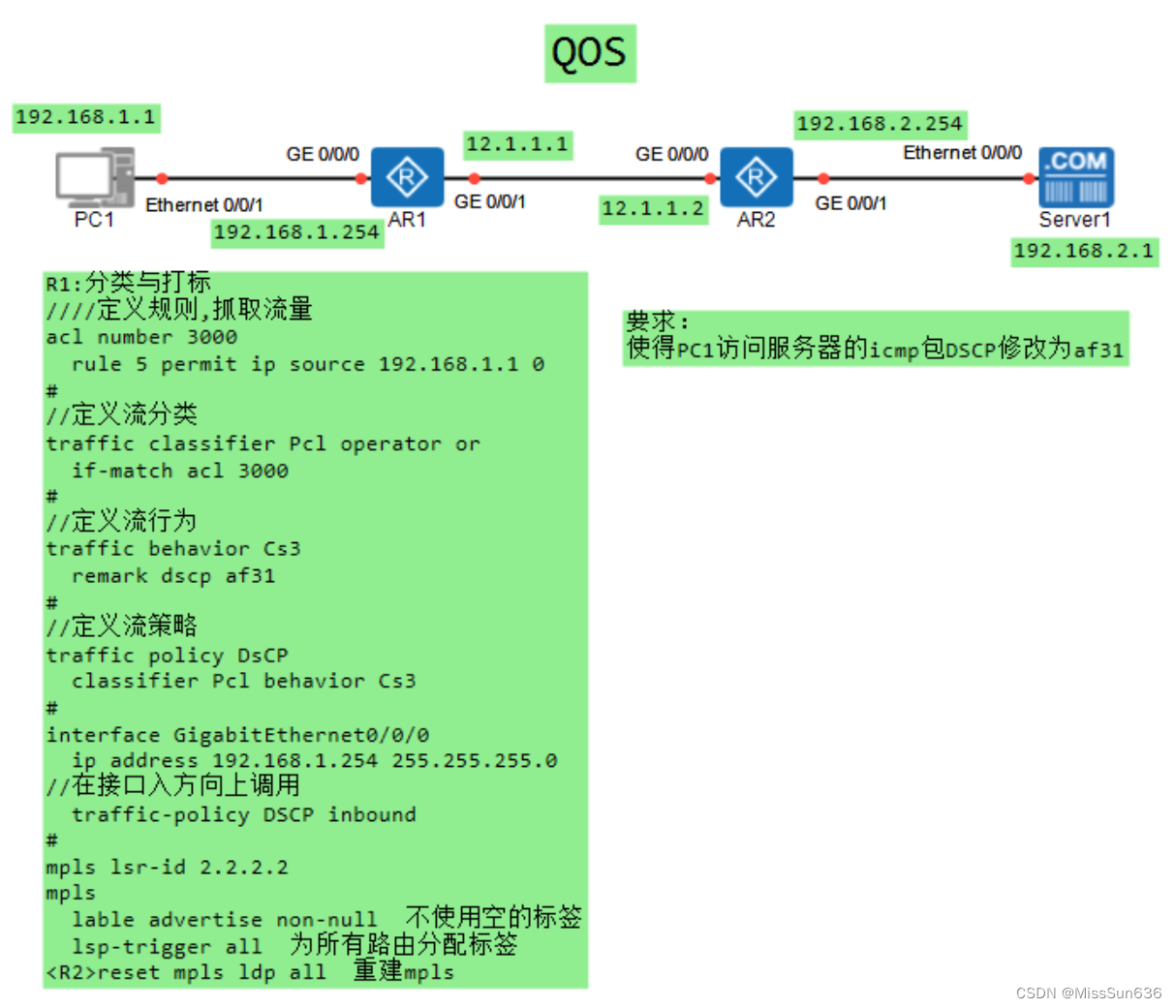
HCIE-QOS基本原理
QOS基本原理 QOS概述什么是QOSQoS服务模型区分服务模型QoS常用技术 (DiffServ模型)QoS数据处理流程 (DiffServ模型) QoS流分类和流标记QoS数据处理流程为什么需要流分类和流标记 简单流分类外部优先级 - VLAN报文外部优先级 - MPLS报文外部优先级 - IP报文各外部优先级间的对应…...
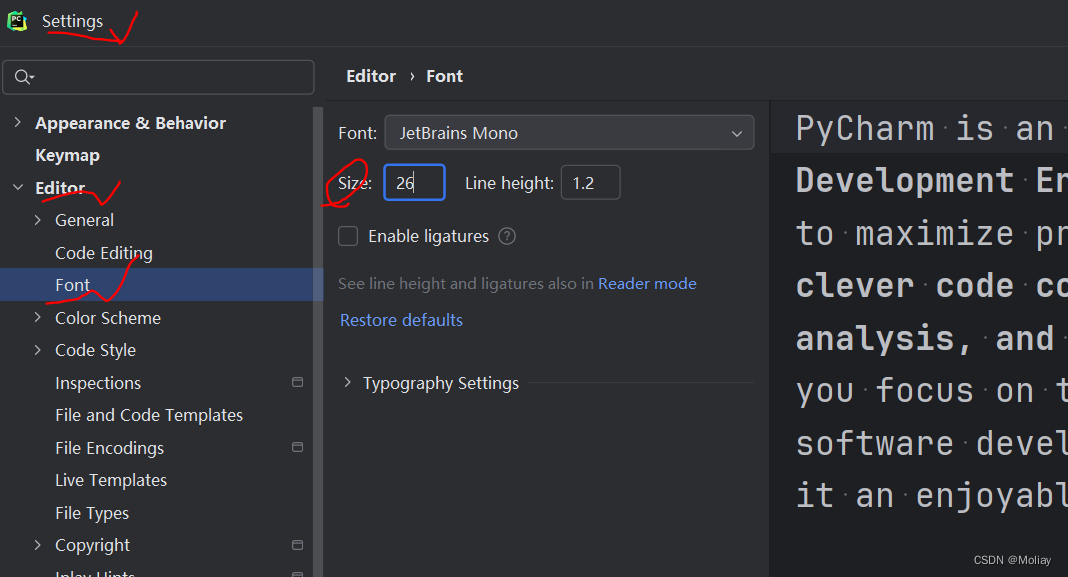
pycharm基本使用(常用快捷键)
0.下载 pycharm官网下载 选择合适的版本,本文以2024.1为例 1.简单应用 常用快捷键 ctrlD 复制当前行 ctrlY 删除当前行 ctrlX 剪切当前行(可用作删除,更顺手) shift↑ 选中多行ctrlshiftF10 运行 shiftF9 调试ctrl/ 注释当前…...
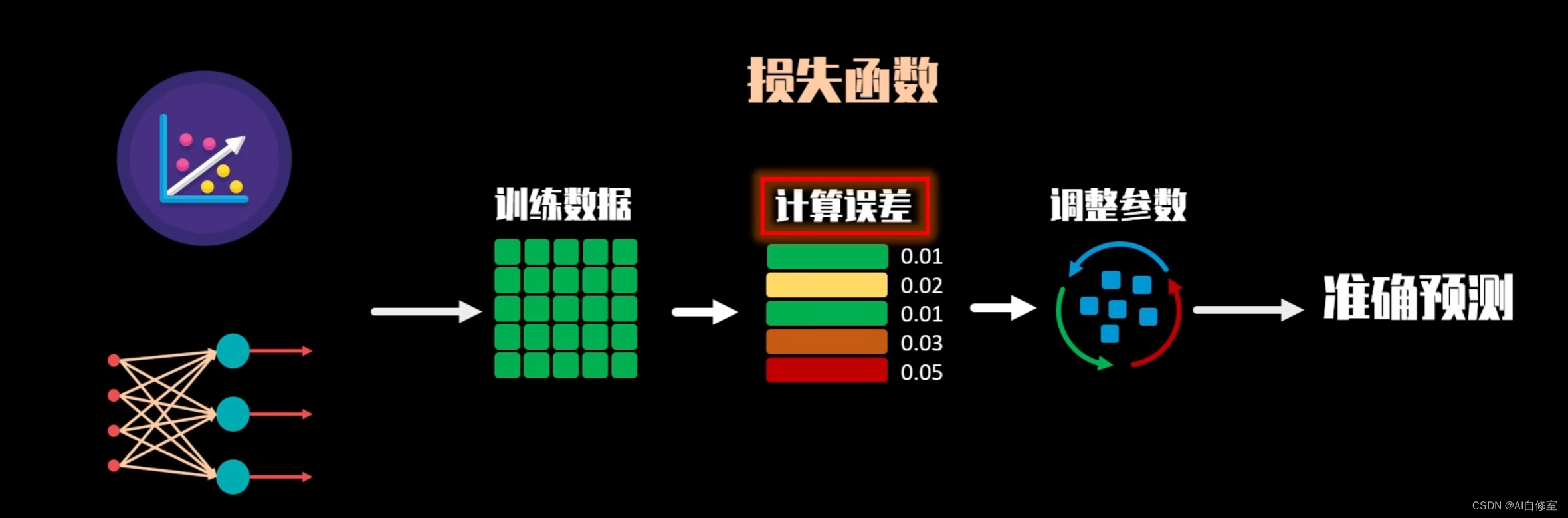
机器学习--回归模型和分类模型常用损失函数总结(详细)
文章目录 引言 回归模型常用损失函数均方误差(Mean Squared Error, MSE)均方根误差(Root Mean Squared Error, RMSE)平均绝对误差(Mean Absolute Error, MAE)Huber损失(Huber Loss) …...

企业选择数字工厂管理系统供应商的标准是什么
随着信息技术的飞速发展,数字化转型已成为企业提升竞争力、实现可持续发展的必由之路。在制造业领域,数字工厂管理系统实现生产流程自动化、智能化的关键工具,其选择的重要性不言而喻。本文将从多个维度探讨企业选择数字工厂管理系统供应商的…...

京准电钟|基于纳秒级的GPS北斗卫星授时服务器
京准电钟|基于纳秒级的GPS北斗卫星授时服务器 京准电钟|基于纳秒级的GPS北斗卫星授时服务器 你有没有思考过这样一个问题:火车站内,熙熙攘攘,旅客排队进站、列车停靠发车,一切井然有序。一旦有个别时间出现…...

Flutter知识点
Dart语言基础知识 Dart特性: Dart 是少数同时支持 JIT(Just In Time,即时编译)和 AOT(Ahead of Time,运行前编译)的语言之一。语言在运行之前通常都需要编译,JIT 和 AOT 则是最常见…...

2024-06-12 问AI: 在大语言模型中,什么是Jailbreak漏洞?
文心一言 在大语言模型中,Jailbreak漏洞(也称为越狱攻击或指令注入攻击)是一种特定的安全漏洞,它允许用户或攻击者通过精心设计的输入或指令,绕过模型的安全限制,诱导模型产生原本被设定为禁止或限制的输出…...

Vue22-v-model收集表单数据
一、效果图 二、代码 2-1、HTML代码 2-2、vue代码 1、v-model单选框的收集信息 v-model:默认收集的就是元素中的value值。 单选框添加默认值: 2、v-model多选框的收集信息 ①、多个选择的多选 注意: 此处的hobby要是数组!&…...

【深度学习】深入解码:提升NLP生成文本的策略与参数详解
文章目录 解码策略解码参数公式解释代码例子区别 更详细的束搜索的解释更详细的例子解释第一步第二步第三步 解码策略和解码参数在自然语言处理(NLP)模型的生成过程中起着不同的作用,但它们共同决定了生成文本的质量和特性。 解码策略 解码…...
Petalinux由于网络原因产生的编译错误(2)--Fetcher failure:Unable to find file
1 Fetcher failure:Unable to find file 错误 如果编译工程遇到如下图所示的“Fetcher failure for URL”或相似错误 出现这种错误的原因是 Petalinux 在配置和编译的时候,需要联网下载一些文件,由于网 络原因这些文件不能正常下载,导致编译…...
随手记:商品信息过多,展开收起功能
UI原型图: 页面思路: 在商品信息最小item外面有一个包裹所有item的标签,控制这个标签的高度来实现展开收起功能 <!-- 药品信息 --><view class"drugs" v-if"inquiryInfoSubmitBtn"><view class"…...
uniapp上传头像并裁剪图片
第一步写上uniapp自带的选择图片button按钮 点击之后会弹出选择图片的方式 拍照或从相册选择图片后将会跳到图片裁剪 然后我们裁剪完之后点击确定在上传图片 这里是上传图片的接口 拿到本地图片 上传的话自己想以那种方式上传都可以...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
