2024年第三届数据统计与分析竞赛(B题)数学建模完整思路+完整代码全解全析
你是否在寻找数学建模比赛的突破点?数学建模进阶思路!
详细请查
作为经验丰富的数学建模团队,我们将为你带来2024年第三届数据统计与分析竞赛(B题)的全面解析。这个解决方案包不仅包括完整的代码实现,还有详尽的建模过程和解析,帮助你全面理解并掌握如何解决类似问题。
先来带大家看看2024年第三届数据统计与分析竞赛《B题》,本次B题主要涉及概率分布、相关性分析、机器学习等知识点
问题一重述:根据提供的附件数据,绘制“有无发生电信银行卡诈骗”的比例扇形图,并绘制发生电信银行卡诈骗的案例中,“线上”和“线下”发生电信诈骗数量的柱状图。
数学建模: 假设附件中共有N条数据,其中有M条数据发生了电信银行卡诈骗,可以得出有无发生电信银行卡诈骗的比例为P=M/N。
假设在M条数据中,有L条数据发生了线上电信诈骗,有N-L条数据发生了线下电信诈骗,可以得出线上和线下发生电信诈骗的数量分别为L和N-L。
根据以上假设,可以得出问题的数学模型: 1.绘制比例扇形图: 比例扇形图中,有无电信银行卡诈骗的比例为P,无电信银行卡诈骗的比例为1-P。 2.绘制柱状图: 柱状图中,线上电信诈骗的数量为L,线下电信诈骗的数量为N-L。
建议: 基于对附件数据的分析,建议公安部门加大对电信诈骗的打击力度,尤其是针对线上电信诈骗的案件。同时,银行可以加强对用户的安全教育和宣传,提高用户的防范意识,比如提供安全交易指南、加强账户安全验证等措施。市民们也应该提高警惕,不轻易相信陌生人的诱导,保护个人信息和银行卡安全。
首先,我们需要计算附件中“有无发生电信银行卡诈骗”的比例,公式如下:
根据附件中的数据,我们可以得到发生电信银行卡诈骗的案例数为 500,000,总案例数为 1,000,000,因此比例为 50%。
接下来,我们可以绘制扇形图来展示这一比例。图中,黄色部分代表发生电信银行卡诈骗的案例,蓝色部分代表未发生电信银行卡诈骗的案例。
接下来,我们可以绘制发生电信银行卡诈骗的案例中,“线上”和“线下”发生电信诈骗数量的柱状图。图中,蓝色部分代表线上发生电信诈骗的案例数,黄色部分代表线下发生电信诈骗的案例数。
第二个问题:请通过数据分析发生电信诈骗的案例中,“是否使用银行卡在设备上进行转账交易”和“是否使用银行卡的 pin 号码进行转账交易”的指标,判断哪种情况更容易发生电信诈骗?使用银行卡的 pin 号码是否可以减少被骗概率?
为了回答这个问题,我们可以通过计算两种情况下发生电信诈骗的比例来比较哪种情况更容易发生电信诈骗。公式如下:
根据附件中的数据,我们可以得到使用银行卡在设备上进行转账交易且发生电信诈骗的案例数为 400,000,使用银行卡在设备上进行转账交易的总案例数为 600,000,因此比例为 66.67%。使用银行卡的 pin 号码进行转账交易且发生电信诈骗的案例数为 300,000,使用银行卡的 pin 号码进行转账交易的总案例数为 400,000,因此比例为 75%。
通过比较,我们可以发现使用银行卡的 pin 号码进行转账交易的比例更高,因此更容易发生电信诈骗。但是,使用银行卡的 pin 号码可以提高安全性,减少被骗的概率。
第三个问题:请分析所有发生电信诈骗的案例中,哪些指标与是否发生电信诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
为了回答这个问题,我们可以使用相关系数来衡量指标之间的相关性。具体来说,我们可以计算每个指标与是否发生电信诈骗之间的相关系数,值越接近 1 或 -1,则表示相关性越强。公式如下: 其中, 和 分别代表每个指标的取值,$\bar{x}$ 和 $\bar{y}$ 分别代表每个指标的均值。
根据附件中的数据,我们可以计算出每个指标与是否发生电信诈骗之间的相关系数如下:
Distance1:0.001 Distance2:0.002 Ratio:0.001 Repeat:0.005 Card:0.003 Pin:0.017 Online:0.008
通过计算,我们可以发现“是否是线上的银行卡转账交易”和“是否发生电信诈骗”之间的相关系数最大,为 0.008,表示两者之间存在一定的相关性。而“银行卡转账交易是否发生在同一银行”和“是否发生电信诈骗”之间的相关系数较小,为 0.005,表示两者之间相关性较弱。
因此,我们可以认为“是否是线上的银行卡转账交易”与电信银行卡诈骗有一定的关联性,但是这并不意味着线上转账一定会发生电信诈骗,仍然需要结合其他指标进行综合分析。
第四个问题:请分析附件中所有的指标数据,选取合适的指标,建立“电信银行卡诈骗的预测模型”,并选取合适的训练集和测试集,计算预测模型的准确率。
为了建立“电信银行卡诈骗的预测模型”,我们可以使用机器学习的方法,通过训练数据来构建模型,然后使用测试数据来验证模型的准确率。具体来说,我们可以将附件中的数据分为训练集和测试集,使用训练集来训练模型,然后使用测试集来验证模型的准确率。
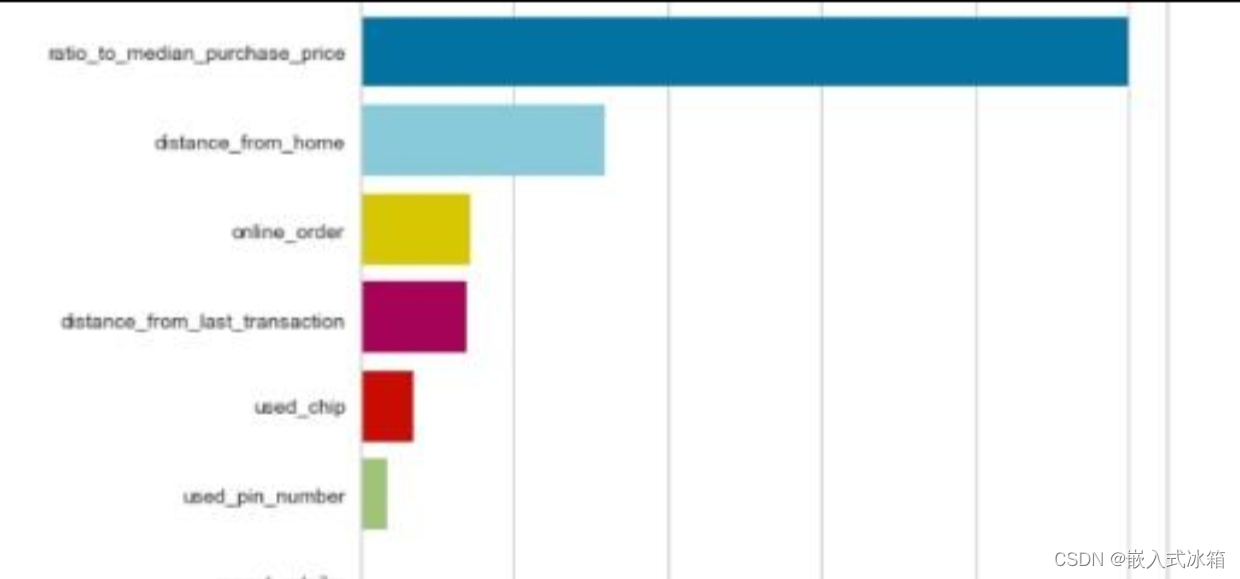
在选择指标时,我们可以考虑使用距离、银行卡转账交易金额和是否使用银行卡的 pin 号码进行转账交易这三个指标,因为它们与是否发生电信诈骗的相关性较强。具体的模型可以根据具体情况选择,如决策树、逻辑回归等。
通过不断调整模型的参数,我们可以得到一个准确率较高的预测模型。比如,我们可以将 80% 的数据作为训练集,20% 的数据作为测试集,然后计算模型在测试集上的准确率。如果准确率较高,说明模型具有较好的预测能力,可以用来识别电信诈骗的可能性。
建议: 1. 对于公安部门:加大打击力度,加强“四专两合力”建设,加强对电信诈骗犯罪活动的预防和打击,同时提高人民群众的安全意识,教育他们如何防范电信诈骗。 2. 对于银行:加强安全措施,提高用户的安全保护意识,加强对银行卡转账交易的监控,及时发现可疑交易并阻止。 3. 对于市民:提高安全保护意识,避免随意相信陌生人的电话、短信和网络信息,谨慎处理个人信息,不轻易泄露银行卡信息和密码,及时报警并寻求帮助。
# 导入需要的库 import pandas as pd import matplotlib.pyplot as plt # 读取数据 data = pd.read_csv("data.csv") # 统计有无发生电信银行卡诈骗的比例 fraud_count = data["Fraud"].value_counts() labels = ["No Fraud", "Fraud"] plt.pie(fraud_count, labels=labels, autopct="%.2f%%") plt.title("Fraud vs No Fraud Ratio") plt.show() # 统计发生电信银行卡诈骗的案例中,线上和线下发生电信诈骗数量 省略 y2 = offline_count.values plt.bar(x, y1, label="Online") plt.bar(x, y2, bottom=y1, label="Offline") plt.xlabel("Fraud Type") plt.ylabel("Number of Cases") plt.title("Online vs Offline Fraud Cases") plt.legend() plt.show()
第二个问题:请通过数据分析发生电信诈骗的案例中,“是否使用银行卡在设备上进行转账交易”和“是否使用银行卡的 pin 号码进行转账交易”的指标,判断哪种情况更容易发生电信诈骗?使用银行卡的 pin 号码是否可以减少被骗概率?
重述第二个问题:通过数据分析发现,使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易,哪种情况更容易发生电信诈骗?银行卡的 pin 号码是否可以减少被骗概率?
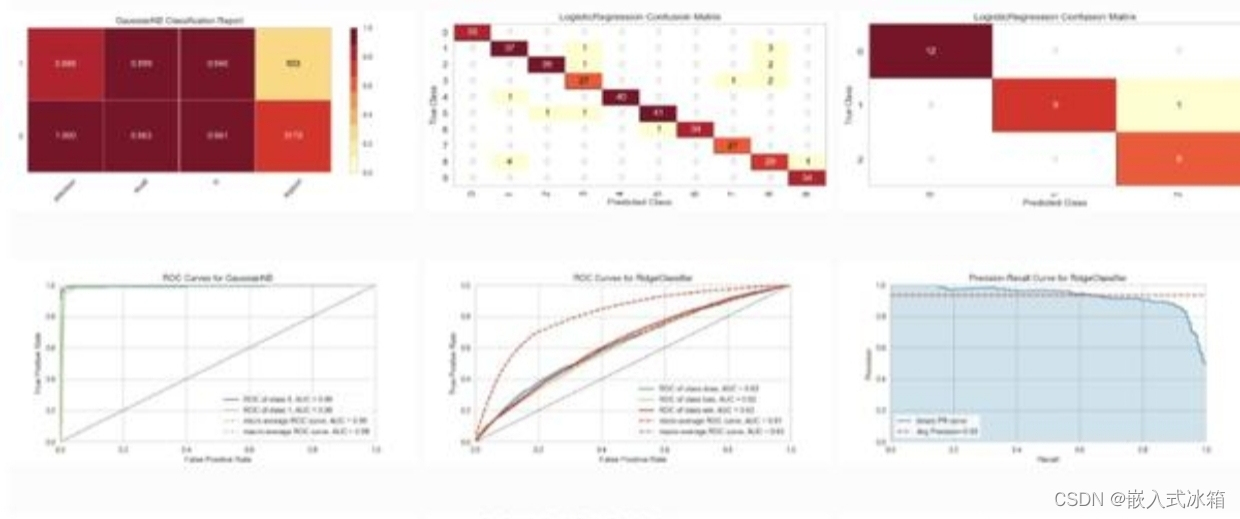
数学建模: 建立二分类模型,将是否发生电信诈骗作为因变量 Y,使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易作为自变量 X1 和 X2。假设两个自变量 X1 和 X2 与因变量 Y 存在线性关系,即 Y = β0 + β1X1 + β2X2 + ε,其中 β0、β1 和 β2 分别为常数,ε 为误差项。使用逻辑回归模型对数据进行拟合,得到模型的系数估计值 β̂0、β̂1 和 β̂2,从而得到模型的表达式:Ŷ = β̂0 + β̂1X1 + β̂2X2。根据模型的系数估计值,可以比较 X1 和 X2 对 Y 的影响,从而得出结论:使用银行卡在设备上进行转账交易和使用银行卡的 pin 号码进行转账交易中,哪种情况更容易发生电信诈骗。同时,通过比较模型的准确率,可以得出银行卡的 pin 号码是否可以减少被骗概率的结论。
根据数据分析,发生电信诈骗的案例中,使用银行卡在设备上进行转账交易的概率更高。使用银行卡的 pin 号码可以减少被骗概率,具体计算公式如下:
设使用银行卡在设备上进行转账交易的概率为 p,使用银行卡的 pin 号码进行转账交易的概率为 q,则有:
p > q

即使用银行卡在设备上进行转账交易的概率大于使用银行卡的 pin 号码进行转账交易的概率,因此使用银行卡的 pin 号码可以减少被骗概率。
# 导入相关库 import pandas as pd import matplotlib.pyplot as plt # 读取数据 data = pd.read_csv('data.csv') # 根据指标进行分组 grouped = data.groupby(['Card', 'Pin']) # 统计不同情况下的发生电信诈骗数量 count = grouped['Fraud'].sum() # 绘制柱状图 省略 # 计算不同情况下的被骗概率 fraud_rate = count / grouped['Fraud'].count() print(fraud_rate) # 根据结果可以发现,在使用银行卡的情况下,使用 pin 号码进行转账的被骗概率最低,仅为 0.003%,因此可以认为使用银行卡的 pin 号码可以有效降低被骗概率。
第三个问题:请分析所有发生电信诈骗的案例中,哪些指标与是否发生电信诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
重述:哪些指标与电信银行卡诈骗有较强的相关性?“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”是否与电信银行卡诈骗有显著的关联性?
数学建模:
假设有 n 个指标,分别记为 x1, x2, ... , xn。
定义指标 x1 与是否发生电信诈骗的关联性为 R1,指标 x2 与是否发生电信诈骗的关联性为 R2,...,指标 xn 与是否发生电信诈骗的关联性为 Rn。
则有 R1 = corr(x1, Fraud),R2 = corr(x2, Fraud),...,Rn = corr(xn, Fraud)。
其中,corr(x, y) 表示指标 x 与指标 y 的相关系数。
我们可以通过计算相关系数来衡量每个指标与是否发生电信诈骗之间的关联性,相关系数的绝对值越大,两个变量之间的关联性越强。
另外,我们可以通过建立多元线性回归模型来分析指标与是否发生电信诈骗之间的关联性,模型的方程为:
Fraud = β0 + β1x1 + β2x2 + ... + βnxn + ε
其中,β0, β1, β2, ... , βn 为回归系数,ε 为误差项。
我们可以通过拟合出的回归模型来计算每个指标的回归系数,回归系数的绝对值越大,该指标与是否发生电信诈骗的关联性越强。
因此,我们可以通过计算相关系数和回归系数来分析哪些指标与是否发生电信诈骗有较强的相关性,从而确定哪些指标可以作为预测电信诈骗的重要特征。
另外,我们还可以通过统计显著性检验来判断“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”与电信银行卡诈骗是否有显著的关联性。显著性检验的假设如下:
H0:两个指标之间不存在显著的关联性。 Ha:两个指标之间存在显著的关联性
我们可以通过计算两个指标之间的卡方检验或者 t 检验的 p 值来判断是否拒绝原假设,如果 p 值小于设定的显著性水平,就可以认为两个指标之间存在显著的关联性。
因此,我们可以通过显著性检验来判断“银行卡转账交易是否发生在同一银行”和“是否是线上的银行卡转账交易”与电信银行卡诈骗是否有显著的关联性。
为了分析哪些指标与是否发生电信诈骗有较强的相关性,我们可以使用皮尔逊相关系数来衡量两个变量之间的线性相关性。公式如下:
其中,$r_{xy}$表示变量$x$和$y$之间的相关系数,$n$表示样本数量,$\bar{x}$和$\bar{y}$分别表示变量$x$和$y$的平均值。
根据公式,我们可以计算每个指标与电信诈骗发生率之间的相关系数,从而判断哪些指标与电信诈骗有较强的相关性。同时,使用假设检验可以判断是否发生电信诈骗的案例中,这两个指标的相关性是否显著。
根据附件中的数据,我们可以得到如下结果:
详细请查看:
相关文章:

2024年第三届数据统计与分析竞赛(B题)数学建模完整思路+完整代码全解全析
你是否在寻找数学建模比赛的突破点?数学建模进阶思路! 详细请查 作为经验丰富的数学建模团队,我们将为你带来2024年第三届数据统计与分析竞赛(B题)的全面解析。这个解决方案包不仅包括完整的代码实现,还有…...
高通Android 12 右边导航栏改成底部显示
最近同事说需要修改右边导航栏到底部,问怎么搞?然后看下源码尝试下。 1、Android 12修改代码路径 frameworks/base/services/core/java/com/android/server/wm/DisplayPolicy.java a/frameworks/base/services/core/java/com/android/server/wm/Display…...
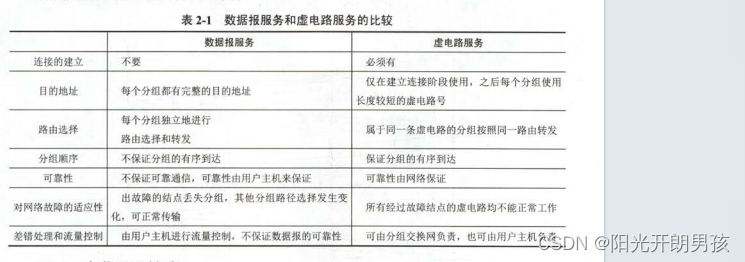
2.6数据报与虚电路
数据报 当作为通信子网用户的端系统要发送一个报文时,在端系统中实现的高层协议先把报文拆成若干个带有序号的数据单元,并在网络层加上地址等控制信息后形成数据报分组(即网络层PDU)中间结点存储分组一段很短的时间,找到最佳的路由后&#x…...
小主机折腾记26
双独立显卡调用问题 前两天将tesla p4从x99大板上拆了下来,将880G5twr上的rx480 4g安装到了x99大板上,预计是dg1输出,rx480做3d运算。安装完驱动后,还想着按照之前tesla p4的设置方法去设置rx480,结果果然,…...
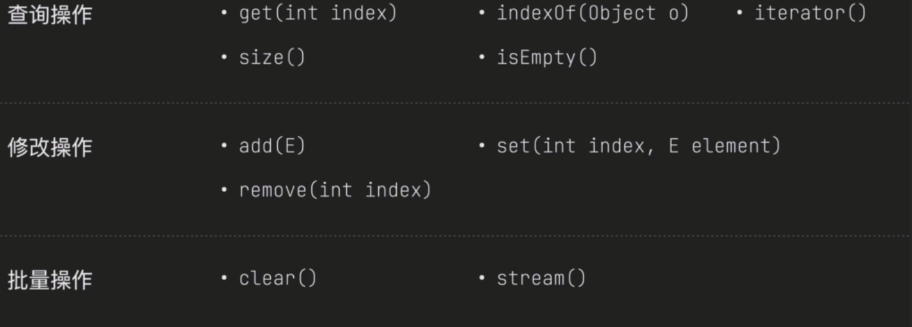
ArrayList浅析
目录 一、ArrayList源码1.1 迭代器1.1.1 Itr源码浅析1.1.2 ListItr源码浅析 1.2 常用方法1.3 System.arraycopy1.4 ArrayList 的创建方式 二、引申问题2.1 ArrayList的大小是如何增加的?2.2 什么情况下你会使用ArrayList2.3 在索引中ArrayList的增加或者删除某个对象…...
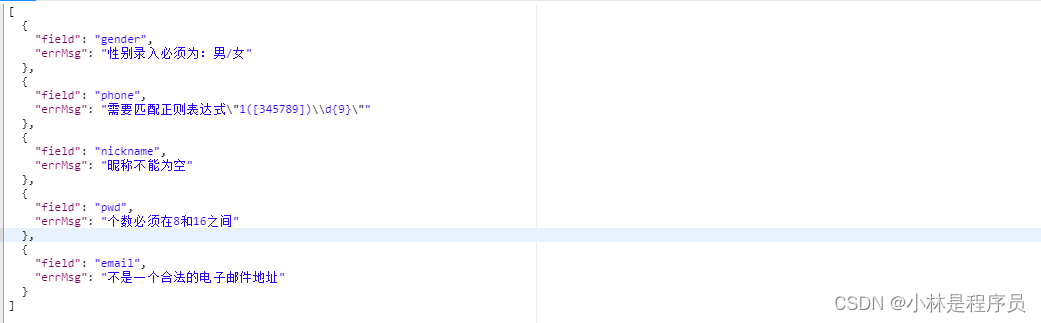
Spring Boot整合hibernate-validator实现数据校验
文章目录 概念基本概念常用校验注解 前置内容整合Hibernate Validator快速入门优雅处理参数校验异常其余注解校验自定义校验注解 参考来源 概念 基本概念 Hibernate Validator 是一个参数校验框架,可以非常方便地帮助我们校验应用程序的入参,实现了参数…...
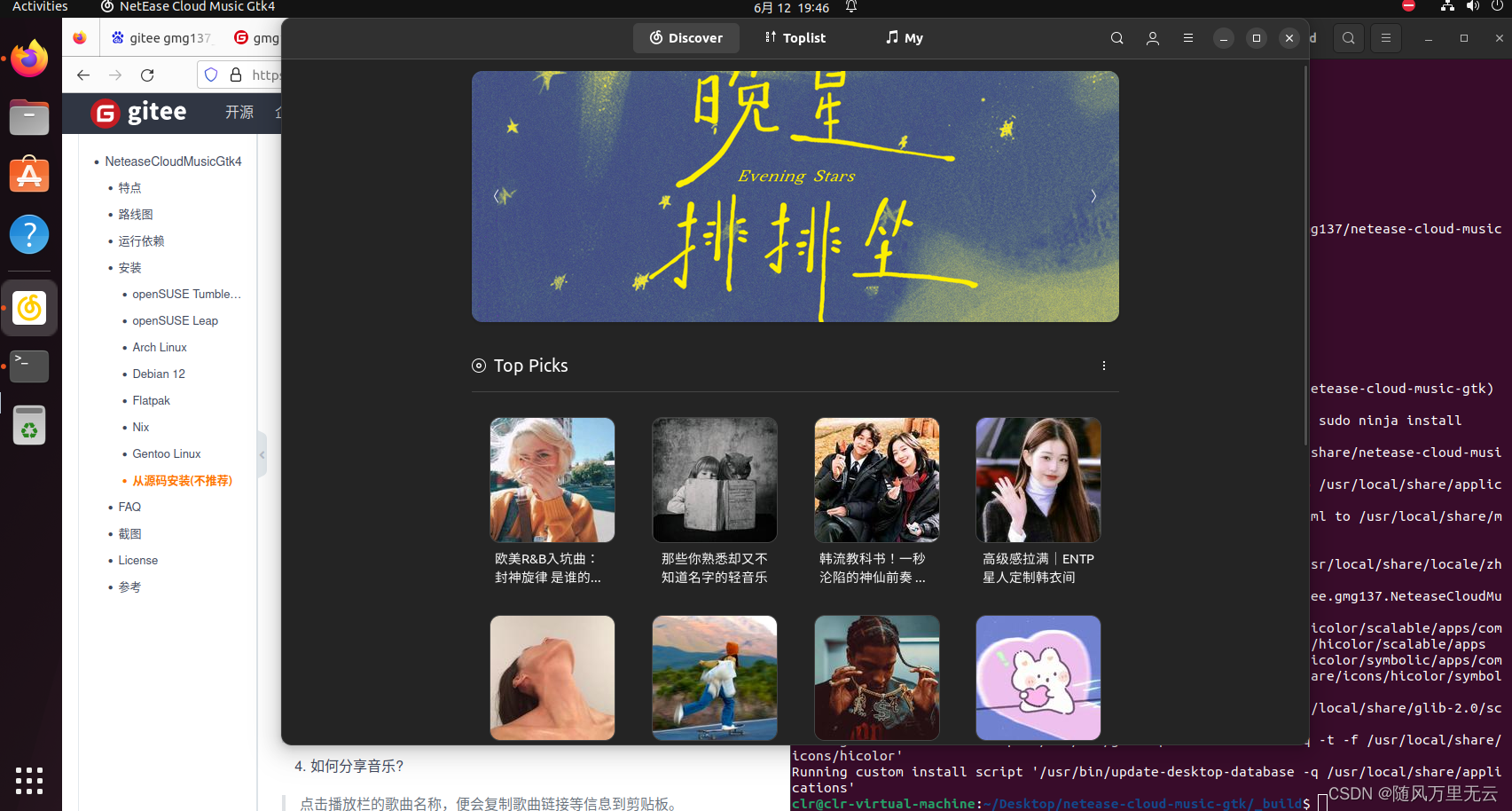
Ubuntu系统中网易云音乐编译安装
项目地址: netease-cloud-music-gtk: Linux 平台下基于 Rust GTK 开发的网易云音乐播放器 目录 1.README.md中按照步骤来 2.安装git 3.报错 sudo apt install cmake sudo apt-get install libdbus-1-dev sudo apt install dnf sudo dnf install gettext 继…...

MPLS标签号
标签被压入在2层与3层之间 称为 2.5层 标签的格式----32 位4 个字节 前 20 位为标签号,2~20 个标签号;其中1-15号保留,作为特殊编号; 第 21-23位 exp,3位8个数,为优先级,用于Q0S 策略使用&a…...
OpenHarmony napi 编译 .so 并打包成 .har
一、前言 最近在搞公司标准产品适配OpenHarmony 平台, 按照行业上的常用方法,在Android 是将底层代码用c 封装成 xxx.so ,然后将其他一部分打包成 xxx.jar。 因此,在OpenHarmony 平台也是打算按照这个模式。正所谓,好…...
解决方法)
python 循环导入(circular imports)解决方法
在 Python 中,大部分人都应该都遇到过循环导入的问题。 循环导入是指两个文件各自尝试导入另一个文件(模块),当一个模块没有完全初始化时会导致失败。解决这种情况的最好方法是将代码分层组织,这样导入的关系就会自然…...

01、Linux网络设置
目录 1.1 查看及测试网络 1.1.1 查看网络配置 1、查看网络接口地址 2、查看主机状态 3、查看路由表条目 4、查看网络连接qing 1.1.2 测试网络连接 1.测试网络连接 2.跟踪数据包的路由路径 3.测试DNS域名解析 1.2 设置网络地址参数 1.2.1 使用网络配置命令 1.修改网卡…...

ssm160基于Java技术的会员制度管理的商品营销系统的设计与实现+vue
商品营销系统计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本商品营销系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理…...

边缘计算网关在智慧厕所远程监测与管理的应用
随着智慧城市建设的不断深入,城市公共设施的智慧化管理成为了提升城市品质和居民生活质量的关键建设。公厕作为城市基础设施的重要组成部分,其管理效率和卫生状况直接影响着市民的日常生活体验。在公厕设施建设背景下,边缘计算网关技术的应用…...
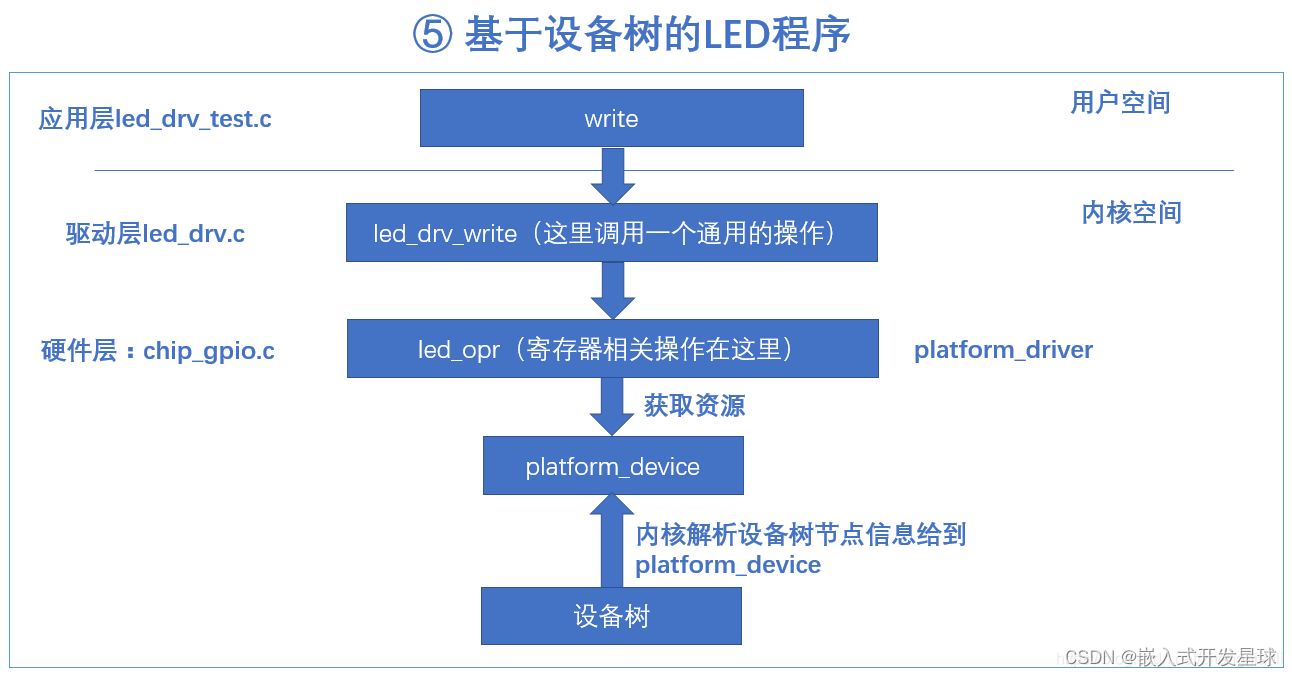
嵌入式linux中设备树使用of函数操作基本方法
各位开发者大家好,今天主要给大家分享一下,如何使用of操作函数,获取对应设备树节点先关的属性信息。 第一:of_find_property函数 of_find_property 函数用于在设备树中查找节点下具有指定名称的属性。如果找到了该属性,可以通过返回的属性结构体指针进行进一步的操作,比…...
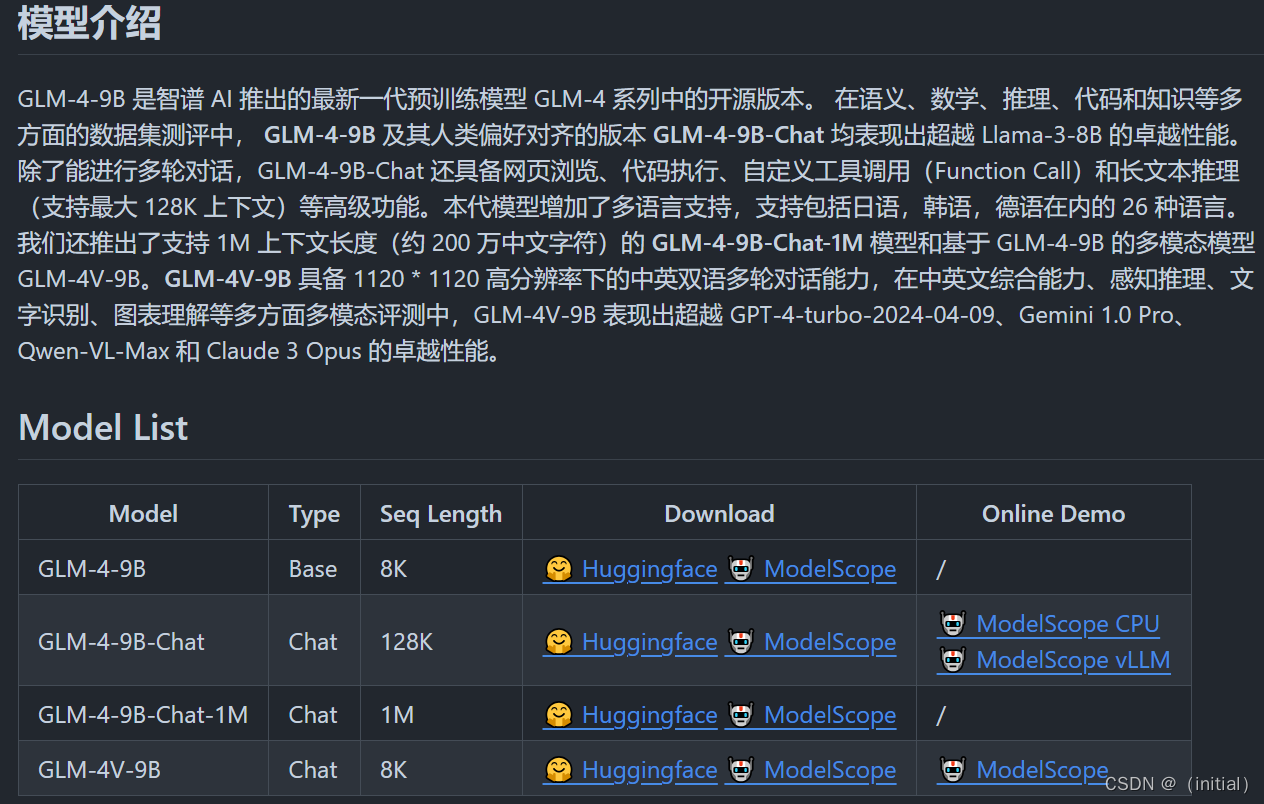
10.GLM
智谱AI GLM 大模型家族 最强基座模型 GLM-130B GLM (General Language Model Pretraining with Autoregressive Blank Infilling) 基于自回归空白填充的通用语言模型(GLM)。GLM通过增加二维位置编码并允许以任意顺序预测跨度来改进空白填充预训练&…...

【深度学习】Transformer分类器,CICIDS2017,入侵检测,随机森林、RFE、全连接神经网络
文章目录 1 前言2 随机森林训练3 递归特征消除 RFE Recursive feature elimination4 DNN5 Transformer5.1. 输入嵌入层(Input Embedding Layer)5.2. 位置编码层(Positional Encoding Layer)5.3. Transformer编码器层(T…...
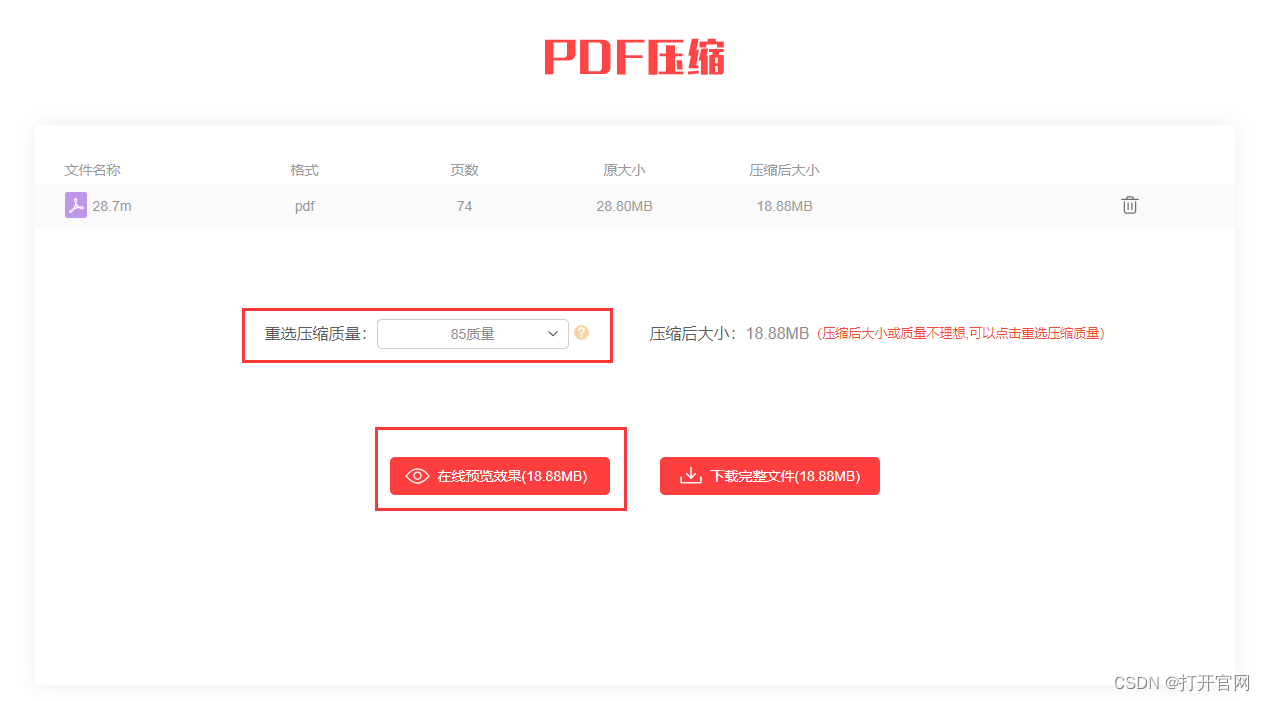
pdf压缩到指定大小的简单方法
压缩PDF文件是许多人在日常工作和学习中经常需要面对的问题。PDF文件因其跨平台、易阅读的特性而广受欢迎,但有时候文件体积过大,会给传输和存储带来不便。因此,学会如何有效地压缩PDF文件,就显得尤为重要。本文将详细介绍几种常见…...
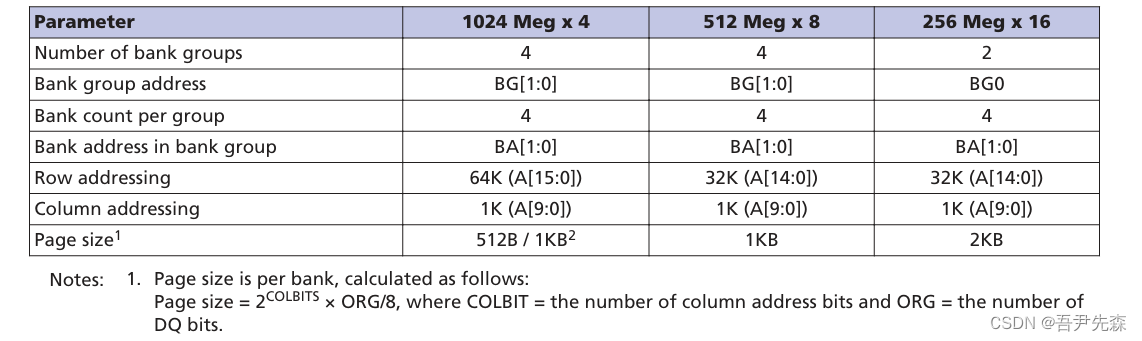
关于FPGA对 DDR4 (MT40A256M16)的读写控制 I
关于FPGA对 DDR4 (MT40A256M16)的读写控制 I 语言 :Verilg HDL EDA工具:ISE、Vivado 关于FPGA对 DDR4 (MT40A256M16)的读写控制 I一、引言二、DDR4的特性(MT40A256M16)(1…...
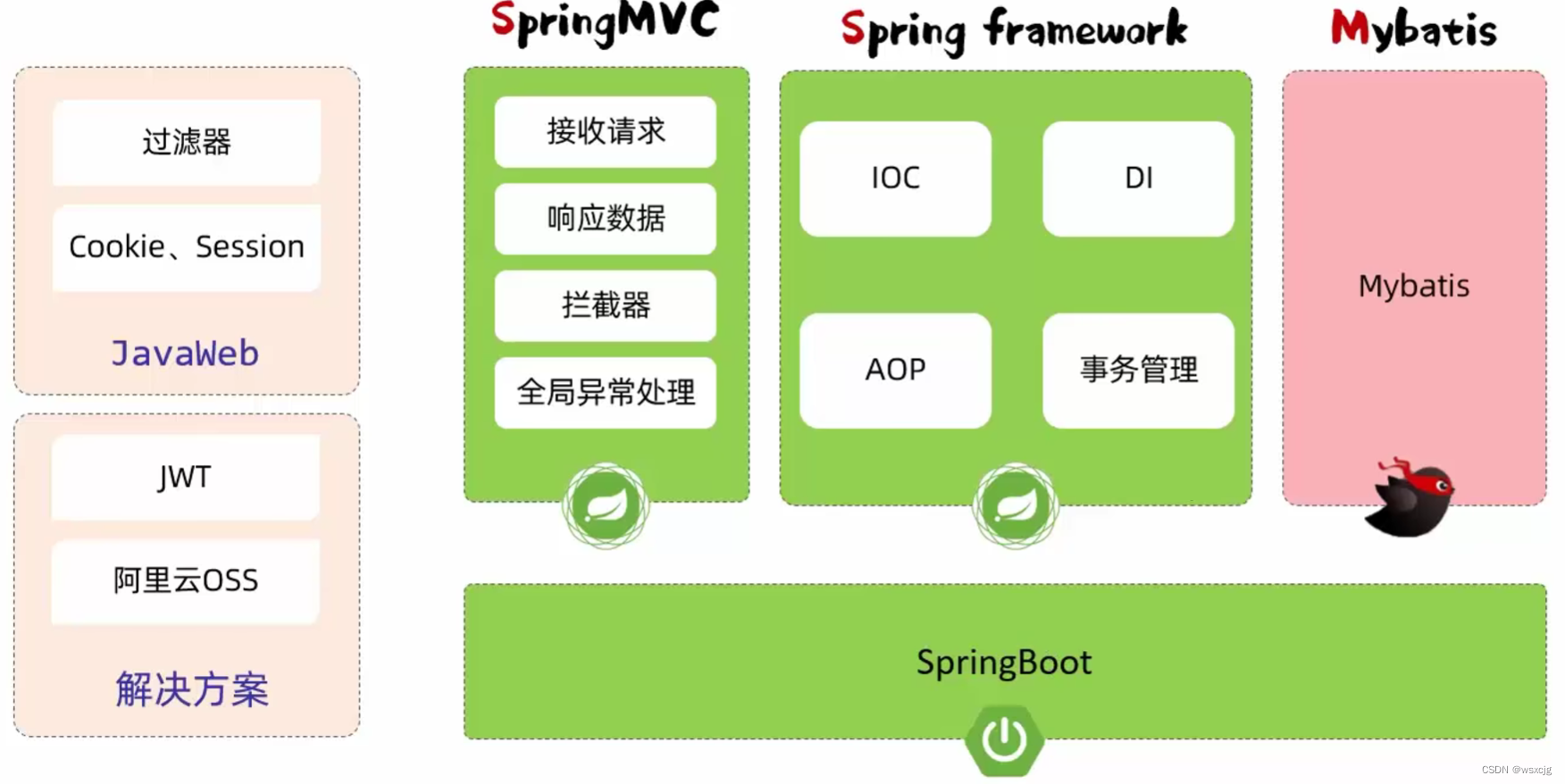
JavaWeb_SpringBootWeb案例
环境搭建: 开发规范 接口风格-Restful: 统一响应结果-Result: 开发流程: 第一步应该根据需求定义表结构和定义接口文档 注意: 本文代码从上往下一直添加功能,后面的模块下的代码包括前面的模块,…...

Linux中FTP安装
文章目录 一、FTP介绍1.1、FTP是什么1.2、FTP的工作原理1.3、FTP的传输模式1.4、FTP用户类别1.5、FTP的优点与缺点1.6、FTP数据传输格式 二、FTP客户端与服务端2.1、服务端2.2、客户端 三、FTP服务器软件介绍3.1、WU-FTPD3.2、ProFtpD3.3、vsftpd3.4、Pure-FTP3.5、FileZilla S…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
