【代码随想录算法训练营第三十五天】 | 1005.K次取反后最大化的数组和 134.加油站 135.分发糖果
贪心章节的题目,做不出来看题解的时候,千万别有 “为什么这都没想到” 的感觉,想不出来是正常的,转变心态 “妙啊,又学到了新的思路” ,这样能避免消极的心态对做题效率的影响。
134. 加油站
按卡哥的思路:
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
这种其实算是暴力解法的优化,相当于利用了前面的信息,当 sum 变成负数时,确认了 [ 0 ,i ] 的点都无法作为起点。
为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零?
证明采用反证法,用卡哥的图来解释
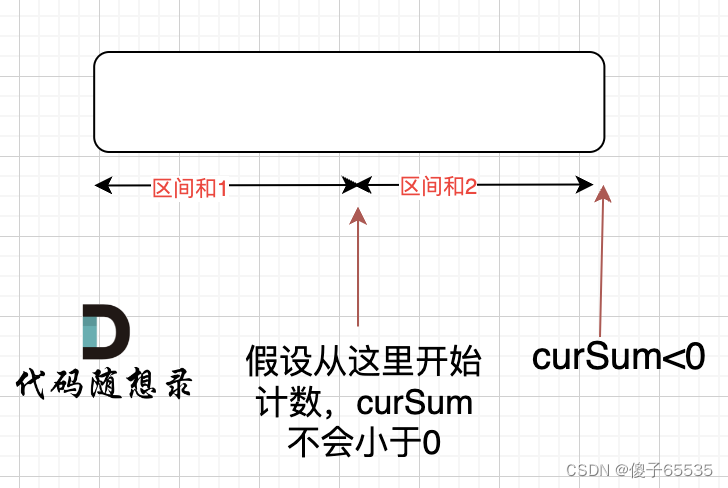
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum = 0;int totalSum = 0;int start = 0;for (int i = 0; i < gas.size(); i++) {curSum += gas[i] - cost[i];totalSum += gas[i] - cost[i];if (curSum < 0) { // 当前累加rest[i]和 curSum一旦小于0start = i + 1; // 起始位置更新为i+1curSum = 0; // curSum从0开始}}if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了return start;}
};本题困扰我很久的地方在于另一种解法,我最开始将 gas[i] - cost[i] 的值做成数组,再利用前缀和的技巧,直观地想到,前缀和最低点的后一个点是最佳起点,以它为起点的后半段一定是能走通的,再保证全程有盈余,就可以走完全程。亏空最严重的一个点必须放在最后一步走,等着前面剩余的救助。
这种思路的想法是比较直觉的,问题在于这个加油站是环形的,怎么证明从不同的起点出发,无论能不能走完全程,全局最低点的位置是不变的。
这个结论的前提条件有点多,但题目都满足:
1、环形的数组。
2、起点可以变化,但数组中的元素及其顺序是固定的。换句话说,我们在分析累积和时并没有改变任何元素的值,只是改变了它们被累加的起始点和顺序。
3、数组的总和要大于0,即题目要求的有解,且必须是唯一解,多解的话这个解法失效,需要添加额外的判定条件。
4、环形数组中的元素是连续分布的,并且在整个分析过程中保持不变。
5、累积和计算方法是线性的,即从选定的起点开始,依次加上下一个元素,直到数组结束,然后继续从数组的开始处累加,直到返回到起点之前的元素。
满足这些条件才能保证,接下来详细说明。
如下图所示,从 0 索引开始的 curSum 的值的变化可以用折线图表示。

满足上述前提的话,在改变起点位置时,如以下标 1 作为起点,我们重新绘制这个折线图,我们能发现,这个图的变化规律—— 起点从 0 变为 1,则将 1 之前的折线拼接到这个图的最右端,这个变化的原因是因为数组是环形的,并且每个位置的值没有改变,所以值的相对大小关系没有改变,只是访问的顺序改变了,导致了折线图的变化。
同时,我们还能发现折线图除了刚刚的把起点左边的折线接在了之前的末尾,折线图也在上下的平移,因为累计值变化了,但除了拼接外,图形的大体形状是没有变化的。
然后我们接着改变起点,我们能发现还是这个变化规律,同时,无论从哪个起点开始,折线图的最低点永远是不变的。
在环形结构中,最低点的不变性基于一个事实:所有可能的前缀和最低值是从数组中某个特定序列的累积得到的,这个序列不会因为起点的改变而改变其累积和的值。虽然累积和的起点改变了,但你依然是在处理同样的一组数值,只是顺序变了。因此,数组中存在的最小和最大累积和出现的位置不会因为起点的改变而改变,它们只是在计算过程中出现的时间变了。每次你重新开始累积时,你都是在重新排列这些相同的值。最低点是由这些值的固定组合决定的,而不是由起点决定的。
这是通过观察折线图得出的结论,并不是严谨的数学证明。
解释完这个结论后,通过折线图来解释这个过程的话,我们在做的就是寻找在遍历所有点时, curSum 都不会小于0,如果存在这样的折线图,那么就找到了唯一解。
public int canCompleteCircuit(int[] gas, int[] cost) {int len = gas.length;int spare = 0;int minSpare = Integer.MAX_VALUE;int minIndex = 0;for (int i = 0; i < len; i++) {spare += gas[i] - cost[i];if (spare < minSpare) {minSpare = spare;minIndex = i;}}return spare < 0 ? -1 : (minIndex + 1) % len;
}这两种思路其实代码都是差不多的,几乎没有不同,只是从两个角度得出的相同的结论。
135. 分发糖果
class Solution {
public:int candy(vector<int>& ratings) {vector<int> candyVec(ratings.size(), 1);// 从前向后for (int i = 1; i < ratings.size(); i++) {if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;}// 从后向前for (int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1] ) {candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);}}// 统计结果int result = 0;for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];return result;}
};这题学习到了前后两次遍历的解法。
这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
先确定右边评分大于左边的情况(也就是从前向后遍历)
再确定左孩子大于右孩子的情况(从后向前遍历)
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。
相关文章:

【代码随想录算法训练营第三十五天】 | 1005.K次取反后最大化的数组和 134.加油站 135.分发糖果
贪心章节的题目,做不出来看题解的时候,千万别有 “为什么这都没想到” 的感觉,想不出来是正常的,转变心态 “妙啊,又学到了新的思路” ,这样能避免消极的心态对做题效率的影响。 134. 加油站 按卡哥的思路…...
桌面应用开发框架比较:Electron、Flutter、Tauri、React Native 与 Qt
在当今快速发展的技术环境中,对跨平台桌面应用程序的需求正在不断激增。 开发人员面临着选择正确框架之挑战,以便可以高效构建可在 Windows、macOS 和 Linux 上无缝运行的应用程序。 在本文中,我们将比较五种流行的桌面应用程序开发框架&…...

学习笔记丨嵌入式BI分析的12个关键功能
编者注:以下内容节选编译自嵌入式分析厂商Qrvey发表的《What is Embedded Analytics?》(什么是嵌入式分析)一文,作者为Qrvey产品市场主管Brian Dreyer。 什么是嵌入式分析? 嵌入式分析是指能够将数据分析的特性和功…...
在使用包含操作符<@和@>时优化范围查询)
PostgreSQL17优化器改进(3)在使用包含操作符<@和@>时优化范围查询
PostgreSQL17优化器改进(3)在使用包含操作符<和>时优化范围查询 本文将介绍PostgreSQL 17服务端优化器在使用包含操作符<和>时优化范围查询。其实在在第一眼看到官网网站的对于该优化点的时候,可能是由于缺乏对于范围类型的认知…...
【因果推断python】32_合成控制2
目录 合成控制作为线性回归的一种实现编辑 合成控制作为线性回归的一种实现 为了估计综合控制的治疗效果,我们将尝试构建一个类似于干预期之前的治疗单元的“假单元”。然后,我们将看到这个“假单位”在干预后的表现。合成控制和它所模仿的单位之间的…...
Linux-笔记 全志平台OTG虚拟 串口、网口、U盘笔记
前言: 此文章方法适用于全志通用平台,并且三种虚拟功能同一时间只能使用一个,原因是此3种功能都是内核USB Gadget precomposed configurations的其中一个选项,只能单选,不能多选,而且不能通过修改配置文件去…...

Qt实现SwitchButton滑动开关按钮组件
概述 使用Qt如何制作一个滑动开关按钮,同类的文章和代码网上很多,但很多都是pyqt编写的,也有c编写的,大家可以参考. 我这里主要是实现了一个滑动按钮,富有滑动动画和文字,话不多说,上代码 自定义…...

C++进阶:继承
文章目录 继承的概念继承的定义方式继承关系和访问限定符基类和派生类对象的赋值转换继承中的作用域派生类中的默认成员函数构造函数拷贝构造函数赋值拷贝函数析构函数 总结 继承的概念 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允…...

SFTP工具
SFTP工具 工具类配置类调用 工具类 Slf4j Component public class SFTPUtils {Resourceprivate SftpConfig sftpConfig;Session session null;Channel channel null;/*** 网络图片url** param fileUrl* throws JSchException*/public String uploadFileSFTP(String fileUrl) …...
服务器数据恢复—vxfs文件系统元数据被破坏的数据恢复案例
服务器存储数据恢复环境: 某品牌MSA2000服务器存储中有一组由8块SAS硬盘组建的raid5磁盘阵列,其中包含一块热备盘。分配了6个LUN,均分配给HP-Unix小机使用。磁盘分区由LVM进行管理,存放的数据主要为Oracle数据库及OA服务端。 服务…...
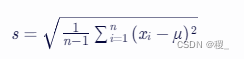
【SCAU数据挖掘】数据挖掘期末总复习题库简答题及解析——上
1.K-Means 假定我们对A、B、C、D四个样品分别测量两个变量,得到的结果见下表。 样品 变量 X1X2 A 5 3 B -1 1 C 1 -2 D -3 -2 利用K-Means方法将以上的样品聚成两类。为了实施均值法(K-Means)聚类,首先将这些样品随意分成两类(A、B)和(C、…...

云时代的Java:在云环境中实施Java的最佳实践
引言 云计算已经成为现代软件开发不可或缺的一部分,它提供了灵活性、可扩展性和成本效益。对于Java开发者来说,掌握在云环境中部署和管理Java应用的最佳实践是至关重要的。本文将探讨一些关键策略,帮助你最大化Java在云平台上的性能和效率。…...

STL - 常用算法
概述: 算法主要是由头文件<algorithm><functional><numeric>组成<algorithm>是所有STL头文件中最大的一个,范围涉及比较、 交换、查找、遍历操作、复制、修改等等<numeric>体积很小,只包括几个在序列上面进行…...
)
Qt | QTextStream 类(文本流)
01、字符编码 1、怎样将字符转换为二进制形式进行存储,存在一个编码的问题,通常都需进行两次编码, 2、字符集:字符的第一次编码是将字符编码为与一个数值(如一个 10 进制整数)相对应,比如把字符 A 编码为 10 进制的 65,B 编码为 66 等。把每一个字符都编码为与一个数值…...

Python学习笔记7:入门知识(七)
前言 之前说过我更换了新的学习路线,现在是根据官方文档和书籍Python crash course来进行学习的,在目前的学习中,对于之前的知识有一些遗漏,这里进行补充。 学习资料有两个,书籍中文版PDF,关注我私信发送…...

如何翻译和本地化游戏?翻译访谈
如何翻译和本地化游戏?这个过程的技术细节有哪些?游戏翻译不同于电影翻译。Logrus IT游戏本地化部门负责人阿列克谢费奥多罗夫(Alexey Fedorov)在接受RUDN语言学系外语系教授和研究人员的采访时谈到了这一点,他是由尤利…...

[C++] 从零实现一个ping服务
💻文章目录 前言ICMP概念报文格式 Ping服务实现系统调用函数具体实现运行测试 总结 前言 ping命令,因为其简单、易用等特点,几乎所有的操作系统都内置了一个ping命令。如果你是一名C初学者,对网络编程、系统编程有所了解ÿ…...

2024网络安全学习路线 非常详细 推荐学习
关键词:网络安全入门、渗透测试学习、零基础学安全、网络安全学习路线 首先咱们聊聊,学习网络安全方向通常会有哪些问题 1、打基础时间太长 学基础花费很长时间,光语言都有几门,有些人会倒在学习 linux 系统及命令的路上&#…...
STM32F103ZET6_HAL_CAN
1定义时钟 2定义按键 按键上拉电阻 3开启串口 4打开CAN(具体什么意思上一篇讲了) 5生成代码 /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief …...

javaWeb项目-ssm+vue网上租车系统功能介绍
本项目源码:java-基于ssmvue的网上租车系统源码说明文档资料资源-CSDN文库 项目关键技术 开发工具:IDEA 、Eclipse 编程语言: Java 数据库: MySQL5.7 框架:ssm、Springboot 前端:Vue、ElementUI 关键技术:springboot、…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
