0107连通分量-无向图-数据结构和算法(Java)
文章目录
- 1 API
- 2 代码实现和分析
- 测试
- 后记
1 API
深度优先搜索下一个直接应用就是找出一幅图中的连通分量,定义如下API。
| public class CC | ||
|---|---|---|
| CC(Graph g) | 预处理构造函数 | |
| boolean | connected(int v, int w) | v和w连通吗 |
| int | count() | 连通分量数 |
| int | id(int v) | v所在的连通分量标识符(0~count()-1) |
2 代码实现和分析
package com.gaogzhen.datastructure.graph.undirected;import com.gaogzhen.datastructure.stack.Stack;
import edu.princeton.cs.algs4.Graph;
import edu.princeton.cs.algs4.Queue;import java.util.*;/*** 无向图连通分量* @author: Administrator* @createTime: 2023/03/08 20:18*/
public class CC {/*** 顶点是否标记数组*/private boolean[] marked;/*** 顶点所在连通分量标志:0~count()-1*/private int[] id;/*** 每个连通分量顶点数量*/private int[] size;/*** 连通分量数量*/private int count;/*** 要处理的无向图*/private Graph graph;/*** 计算给定无向图的连通分量* @param graph 指定的无向图*/public CC(Graph graph) {this.graph = graph;int len = graph.V();// 初始化marked = new boolean[len];id = new int[len];size = new int[len];// 搜索连通分量bfs();}/*** 深度优先搜索连通分量*/private void dfs() {// 深度优先非递归实现,借助栈Stack<Iterator<Integer>> c = new Stack<>();// 搜索连通分量for (int v = 0; v < graph.V(); v++) {// 遍历图中所有顶点,以没有被标记过的顶点为起点,搜索连通分量// 执行完一次bsf,标记一个包含顶点v的连通分量if (!marked[v]) {dfs(c, v);// 连通分量标记+1count++;}}}/*** 深度优先搜索连通分量* @param v 起点*/private void dfs(Stack<Iterator<Integer>> c, int v) {if (!marked[v]) {// 起点未标记,标记计数加1// 起点默认没标记,可以不加是否标记判断marked[v] = true;id[v] = count;size[count]++;Iterable<Integer> iterable = graph.adj(v);Iterator<Integer> it;if (iterable != null && (it = iterable.iterator()) != null){// 顶点对应的邻接表迭代器存入栈c.push(it);}}while (!c.isEmpty()) {Iterator<Integer> it = c.pop();int x;while (it.hasNext()) {// 邻接表迭代器有元素,获取元素x = it.next();if (!marked[x]) {// 顶点未被标记,标记计数+1marked[x] = true;id[x] = count;size[count]++;if (it.hasNext()) {// 邻接表迭代器有元素重新入栈c.push(it);}// 深度优先原则,当前迭代器入栈,新标记顶点的邻接表迭代器入栈,下次循环优先访问Iterable<Integer> iterable = graph.adj(x);if (iterable != null && (it = iterable.iterator()) != null){c.push(it);}break;}}}}/*** 广度优先搜索连通分量*/private void bfs() {// 广度优先非递归实现,借助队列Queue<Integer> q = new Queue<>();// 搜索连通分量for (int v = 0; v < graph.V(); v++) {// 遍历图中所有顶点,以没有被标记过的顶点为起点,搜索连通分量// 执行完一次bsf,标记一个包含顶点v的连通分量if (!marked[v]) {bfs(q, v);// 连通分量标记+1count++;}}}private void bfs(Queue<Integer> q, int v) {marked[v] = true;id[v] = count;size[count]++;q.enqueue(v);while (!q.isEmpty()) {Integer x = q.dequeue();for (Integer w : graph.adj(x)) {if (!marked[w]) {marked[w] = true;id[w] = count;size[count]++;q.enqueue(w);}}}}/*** 给定顶点所在的连通分量标记* @param v 给定顶点* @return 顶点所在的连通分量标记* @throws IllegalArgumentException unless {@code 0<= v < V}*/public int id(int v) {validateVertex(v);return id[v];}/*** 顶点v和w是否连通(是否在同一个连通分量内)* @param v 顶点v* @param w 顶点w* @return {@code true} 如果{@code v}和{@code w}在同一个连通分量内;否则{@code false}* @throws IllegalArgumentException unless {@code 0 <= v < V}* @throws IllegalArgumentException unless {@code 0 <= w < V}*/public boolean connected(int v, int w) {validateVertex(v);validateVertex(w);// 如果v和w在同一连通分量,那么连通分量标记相等;否则falsereturn id[v] == id[w];}/*** 返回无向图{@code graph}中连通分量数量* @return 返回无向图{@code graph}中连通分量数量*/public int count() {return count;}/*** 检查指定的顶点是否是有效顶点* @param v 给定顶点* @throws IllegalArgumentException unless {@code 0<= v < V}*/private void validateVertex(int v) {int V = marked.length;if (v < 0 || v >= V) {throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}}public void display() {Map<Integer, ArrayList<Integer>> map = new HashMap<>(count);for (int i = 0; i < count; i++) {map.put(i, new ArrayList<>());}for (int i = 0; i < id.length; i++) {int k = id[i];ArrayList<Integer> list = map.get(k);list.add(i);map.put(k, list);}System.out.println("分量标记\t顶点数量\t顶点");for (int i = 0; i < count; i++) {ArrayList<Integer> l = map.get(i);System.out.println(i +"\t\t" + l.size() + "\t\t" + l);}}
}
这里广度优先搜索和深度优先搜索都能完成连通分量的搜索和标记,这里以广度优先搜索为例,简单讲解下算法。
说明:
- 算法第四版给出的是深度优先的递归版本实现,我们这里给出了非递归的广度优先搜索和深度优先搜索实现。
- 每次bfs(q, v)一定能保证完成包含顶点v的这个连通分量的搜索,这样外层for遍历所有顶点,在该连通分量的顶点(被标记)不在执行bfs;不在该连通分量的顶点(未被标记),一定是属于其他连通分量。直至遍历结束。
- bsf(q,v)通过先标记起点v,在标记和顶点v距离1条边的顶点,2条边的顶点,依次类推,直到标记所有连通的顶点。
- bfs(q, v)内顶点都属于同一连通分量,id[]记录这些顶点对应的连通分量标记就相同;每标记一个顶点,相应的记录该连通分量size[]顶点数量+1。
思考:
- 这里为什么即可以用广度优先又可以用深度优先呢?
命题C。深度优先搜索和广度优先搜索的预处理使用的时间和空间与V+E成正比且可以在常数时间内处理关于图的连通性查询。
证明。有代码可以知道每个邻接表的元素都只会被检查一次,共有2E个元素(每条边2个)。
测试
测试代码:
public static void testCC() {String path = "H:\\gaogzhen\\java\\projects\\algorithm\\asserts\\tinyG.txt";In in = new In(path);Graph graph = new Graph(in);CC cc = new CC(graph);int v = 0, w = 5;System.out.println("顶点 " + v + " 和顶点 " + w + "是否连通:" + cc.connected(v, w));System.out.println("顶点 " + w + "连通分量标记:" + cc.id(w));System.out.println("连通分量数量:" + cc.count());cc.display();
}
测试结果:
顶点 0 和顶点 5是否连通:true
顶点 5连通分量标记:0
连通分量数量:3
分量标记 顶点数量 顶点
0 7 [0, 1, 2, 3, 4, 5, 6]
1 2 [7, 8]
2 4 [9, 10, 11, 12]
后记
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p344-348.
相关文章:
)
0107连通分量-无向图-数据结构和算法(Java)
文章目录1 API2 代码实现和分析测试后记1 API 深度优先搜索下一个直接应用就是找出一幅图中的连通分量,定义如下API。 public class CCCC(Graph g)预处理构造函数booleanconnected(int v, int w)v和w连通吗intcount()连通分量数intid(int v)v所在的连通分量标识符(0~count()-…...
[学习笔记]黑马程序员python教程
文章目录思维导图Python基础知识图谱面向对象SQL入门和实战Python高阶技巧第一阶段第九章:Python异常、模块与包1.9.1异常的捕获1.9.1.1 为什么要捕获异常1.9.1.2 捕获常规的异常1.9.1.3 捕获指定的异常1.9.1.4 捕获多个异常1.9.1.5 捕获全部异常1.9.1.6 异常的else…...

如何配置用于构建 FastReport Online Designer 的 API ?
FastReport Online Designer 是一个跨平台的报表设计器,允许通过任何平台的移动设备创建和编辑报表。今天我们就一起来看看在2023版中新增和改进的功能有哪些,点击下方可以获取最新版免费试用哦! FastReport Onlin Designe最新版试用https:/…...
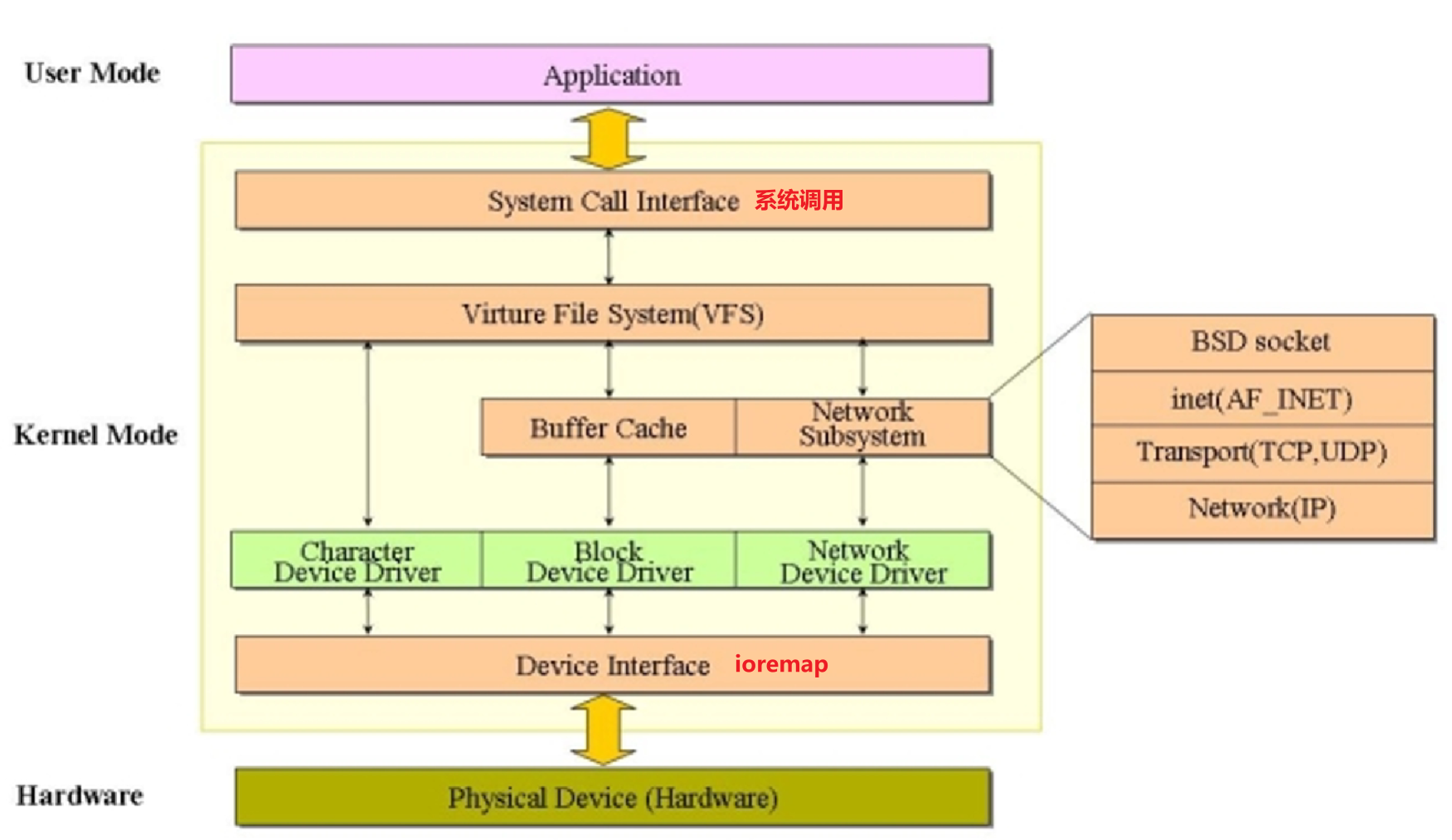
【嵌入式Linux内核驱动】02_字符设备驱动
字符设备驱动 〇、基本知识 设备驱动分类 (按共性分类方便管理) 1.字符设备驱动 字符设备指那些必须按字节流传输,以串行顺序依次进行访问的设备。它们是我们日常最常见的驱动了,像鼠标、键盘、打印机、触摸屏,还有…...

【零散整理】
1-1 git查看代码的项目总行数 git log --prettytformat: --numstat | awk ‘{ add $1; subs $2; loc $1 - $2 } END { printf “added lines: %s, removed lines: %s, total lines: %s\n”, add, subs, loc }’ - 1-2 cookie const cookies document.cookie.split(; )for…...
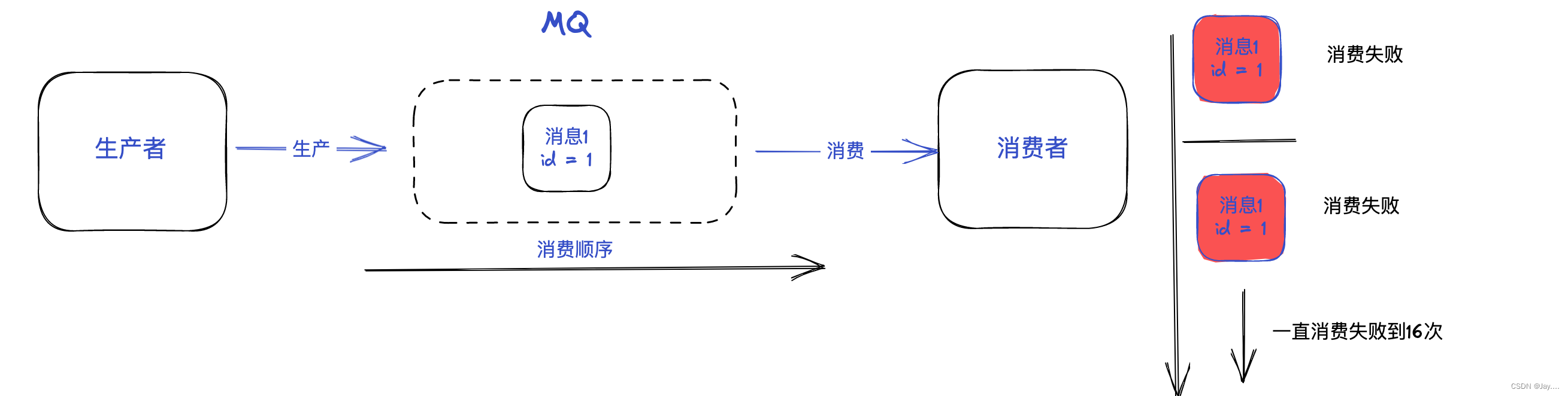
RocketMQ重复消费的症状以及解决方案
RocketMQ重复消费的症状以及解决方案 生产消息时重复 症状 当一条消息已被成功发送到 消费者 并完成持久化,此时出现了网络闪断或者客户端宕机,导致服务端对客户端应答失败。 如果此时 生产者 意识到消息发送失败并尝试再次发送消息,消费者…...
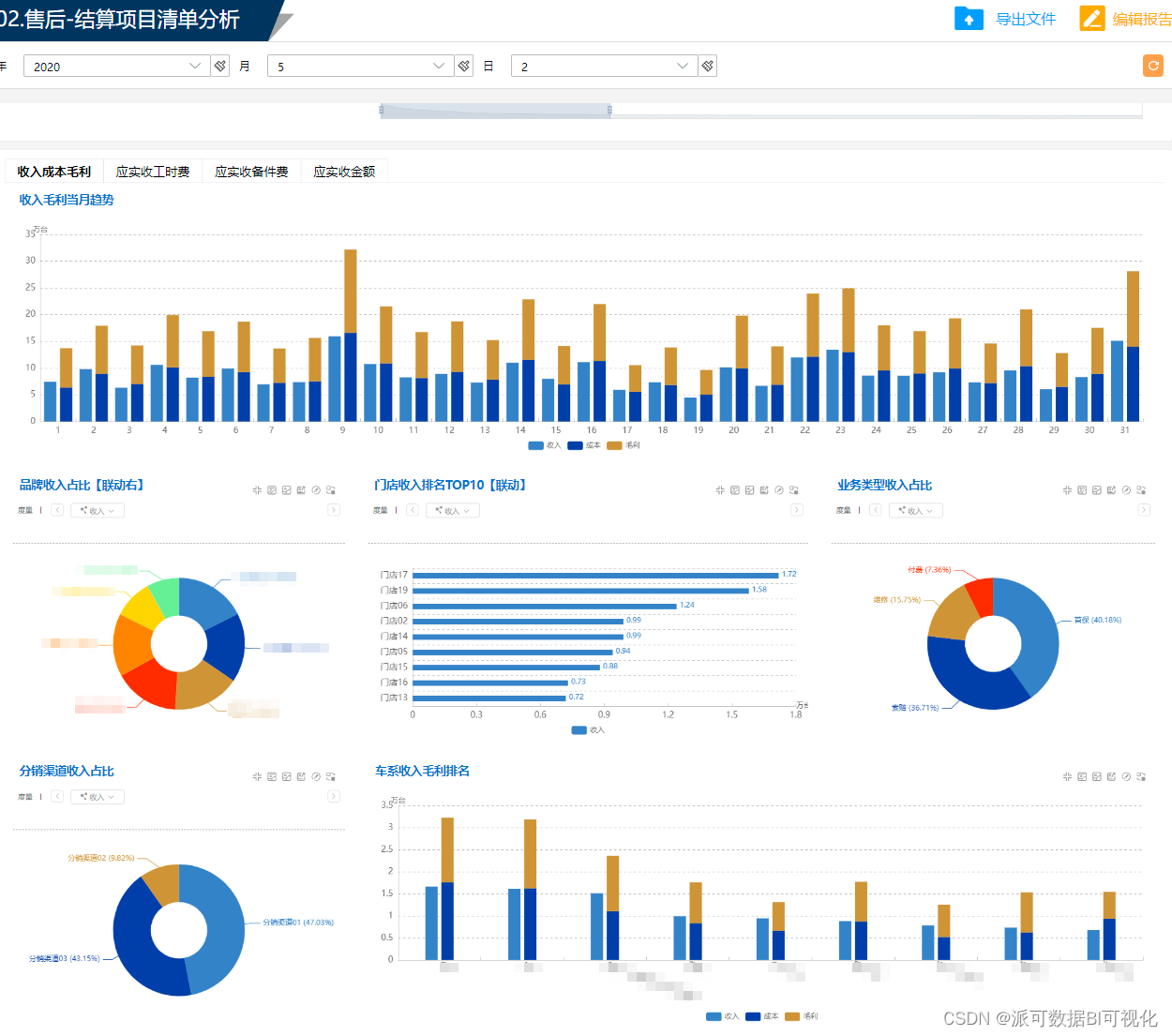
数字化时代,企业的商业模式建设
随着新一代信息化、数字化技术的应用,众多领域通过科技革命和产业革命实现了深度化的数字改造,进入到以数据为核心驱动力的,全新的数据处理时代,并通过业务系统、商业智能BI等数字化技术和应用实现了数据价值,从数字经…...
项目实战典型案例23——-注册上nacos上的部分服务总是出现频繁掉线的情况
注册上nacos上的部分服务总是出现频繁掉线的情况一:背景介绍二:思路&方案解决问题过程涉及到的知识nacos服务注册和服务发现一:背景介绍 spring cloud项目通过nacos作为服务中心和配置中心,出现的问题是其中几个服务总是出现…...
玩转金山文档 3分钟让你的文档智能化
在上个月底,我们给大家推荐了金山轻维表的几个使用场景,社群中不少用户反响很好,对其中一些场景的解决方案十分感兴趣。但也有一些人表示,有些场景不知道如何实现,希望我们能提供模版/教程。这次我们将做一期热门模板盘…...

安装了nodejs怎么安装nvm
第一步,从控制面板卸载已经安装的node 第二步,删除C盘program开头文件夹下的node文件 第三步,去C/user/用户名 文件夹下,删除.npmrc文件 第四步,打开隐藏文件,第三步文件夹下有一个Appdata文件ÿ…...

java安全编码规范考试
java安全编码规范考试 整理不易,收点币!! 安全编码规范考试.md 下面对zip文件的安全解压缩描述,错误的是 A.zip文件解压时,可以使用entry.getSize()对解压缩文件进行文件大小判断 B.zip文件解压时&…...

表格检测识别技术的发展历程
近年来,随着计算机技术的飞速发展,越来越多的研究者开始关注表格检测识别技术。表格检测识别技术是一种利用计算机自动处理表格的技术,它可以实现从文本中检测出表格,并进行识别和提取。这种技术有助于提高文本处理的效率…...
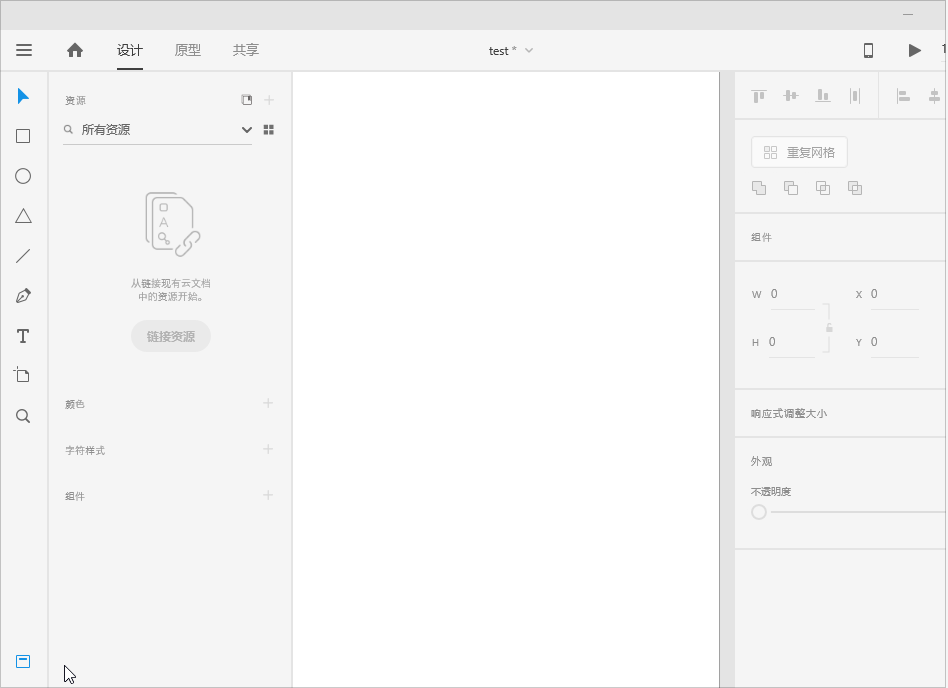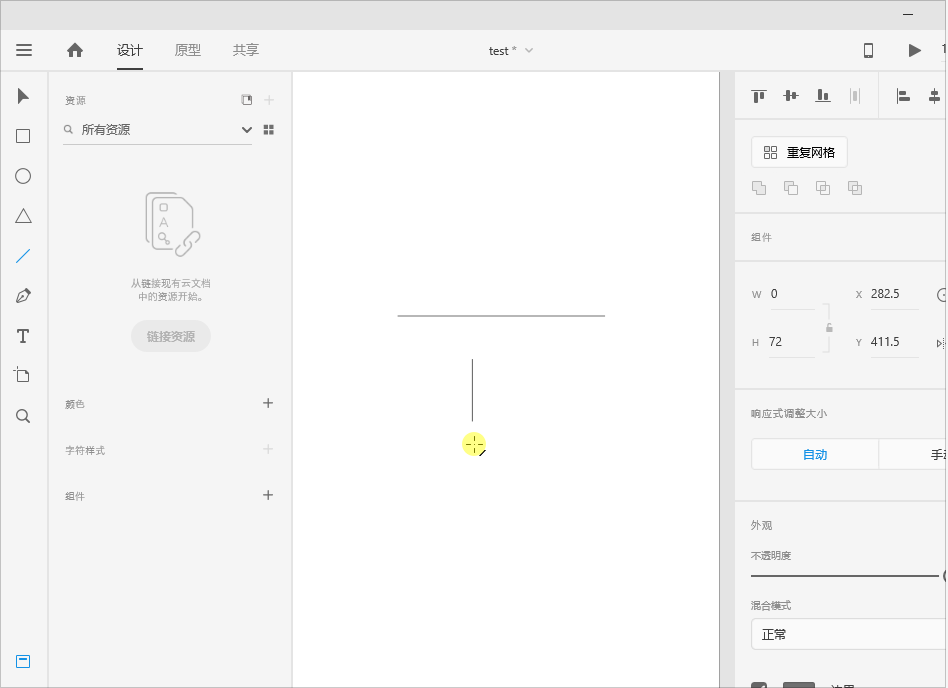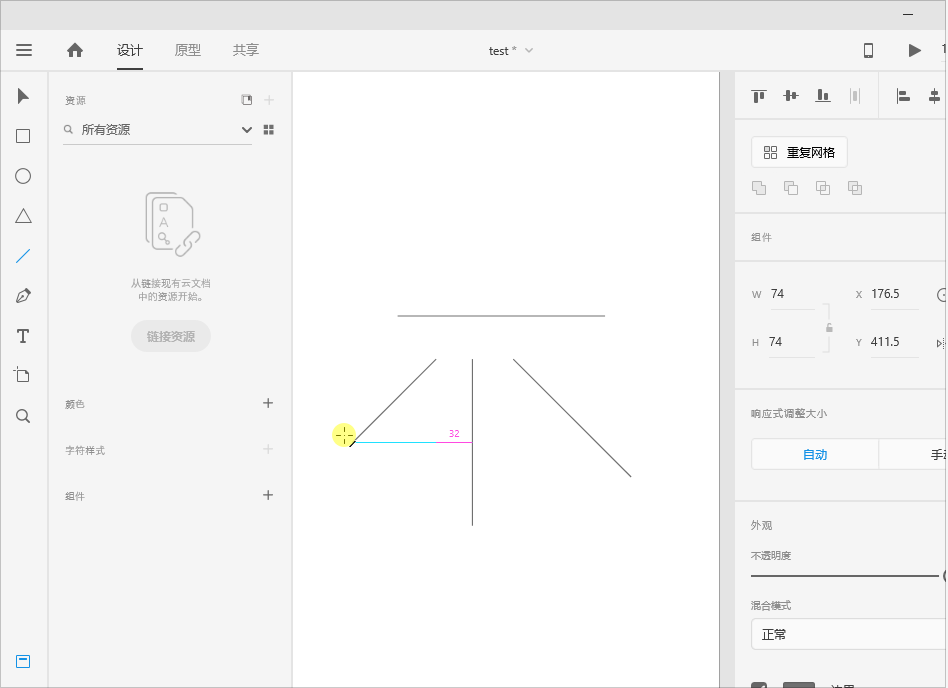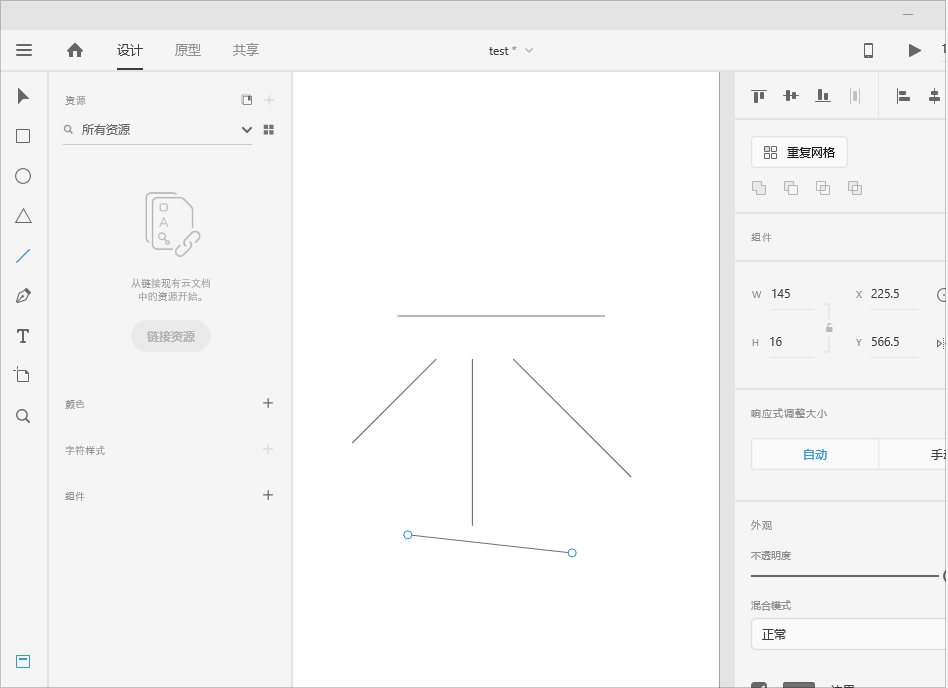
设计UI - Adobe xd对象介绍
矩形工具 新建矩形 操作步骤:选择矩形工具,快捷键R,鼠标在画板上拖出矩形即可。 拖动定界框周围圆形手柄,可快速调整矩形大小,也可以输入宽和高的参数对矩形大小进行改变。 移动矩形 操作步骤:选择选择工具…...

优思学院|精益生产中的“单件流”真的能够做到吗?
精益生产中提到的“一个流”(One Piece Flow)是一种生产方式,它的核心理念是通过合理配置作业场地、人员和设备,使产品从投入到成品产出的整个制造加工过程中始终处于不停滞、不堆积、不超越,按节拍一个一个地流动。 …...
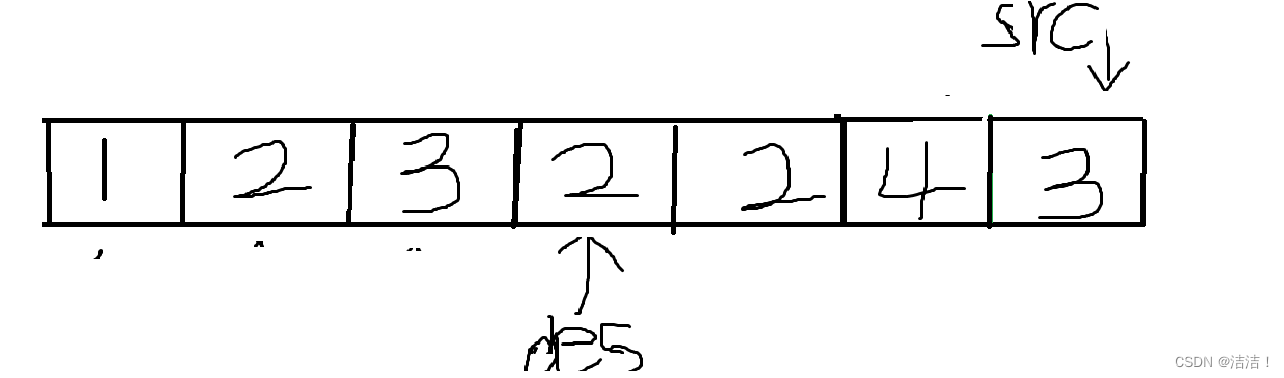
移除元素问题解决方法------LeetCode-OJ题
问题: 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 要求: 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改…...
)
JavaScript学习笔记(1.0)
push() 语法:数组.push(数据) 作用:将数据追加到数组的末尾 返回值:追加数据后数组最新的长度 pop() 语法:数组.pop() 作用:删除数组最后一个数据 返回值:被删除的数据 unshift() 语法:数…...

FCN网络介绍
目录前言一.FCN网络二.网络创新点前言 在图像分割领域,有很多经典的网络,如MASK R-CNN,U-Net,SegNet,DeepLab等网络都是以FCN为基础进行设计的。我们这里简单介绍一下这个网络。 一.FCN网络 FCN网络介绍 FCN 即全…...
Idea+maven+spring-cloud项目搭建系列--11 整合dubbo
前言: 微服务之间通信框架dubbo,使用netty (NIO 模型)完成RPC 接口调用; 1 dubbo 介绍: Apache Dubbo 是一款 RPC 服务开发框架,用于解决微服务架构下的服务治理与通信问题,官方提…...

2023年上半年北京杭州/广州深圳软考中/高级报名入口
软考是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资格考试。 系统集成…...

jupyter notebook配置和使用
简介 Jupyter Notebook是基于网页的用于交互计算的应用程序。其可被应用于全过程计算:开发、文档编写、运行代码和展示结果。 参考博客:https://zhuanlan.zhihu.com/p/33105153 特点 ①编程时具有语法高亮、缩进、tab补全的功能。 ② 可直接通过浏览器…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
