线代知识点总结
目录
一.初等行/列变换
1.计算行列式时,行列变换都可
2.求矩阵的秩时,行列变换都可
3.解线性方程组时,仅能使用初等行变换
4.判定解的情况,单纯求r(A),r(A,b)的过程行列变换都可
5.求向量组极大无关组、线性表出关系,则仅行变换
6.求向量组的秩时,行列变换都可
7.求特征值时,行列变换都可
8.求特征向量时,仅做行变换
9.求逆矩阵时,对(A,E)仅做初等行变换
总结:
二.要牢记
三.某某子式
1.余子式
2.代数余子式
3.k阶子式
4.k阶主子式
5.顺序主子式
四.矩阵的秩
五.常用特征值与特征向量
1.矩阵的逆
2.矩阵的伴随
六.矩阵,向量组,方程组
1.怎么判断两个矩阵等价
2.怎么判断两个向量组是等价向量组
3.同解方程组
七.齐次线性方程组和非齐次线性方程组
八.对比记忆
九.相似与正交
十.合同
十一.二次型
十二.二次型正定
本节是线代某些知识点总结,可能较零碎。
对于简单的知识点,例如“两行对应成比例,行列式为0"就不讲了。暂时不举例题,有时间会继续补充!
一.初等行/列变换
1.计算行列式时,行列变换都可
因为,所以不论动行/列都是等价的。
变换规则:
1.“倍乘”:行列式的某行(列)乘某个元素k。相应的,若行列式中某行(列)元素有公因子k(k≠0),则k可提到行列式外面,即:
2."互换":行列式中两行(列)互换,行列式变号。
3.“倍加”:某行(列)的k倍加到另一行(列),行列式不变。
2.求矩阵的秩时,行列变换都可
因为初等变换不改变某个矩阵非零子式的最高阶数,秩指的就是非零子式的最高阶数。
初等变换的规则:
1."倍乘":一个非零常数乘矩阵矩阵的某一行(列)。
2."互换":互换矩阵中某两行(列)的位置。
3."倍加":将矩阵的某一行(列)的k倍加到令一行(列)。
注意:
某矩阵乘元素k,是矩阵中的每个元素都成k,要与行列式区分。
也就是
。
3.解线性方程组时,仅能使用初等行变换
因为矩阵的每一种初等行变换都对应着线性方程组的同解变换,而作列变换会改变原来的方程。

4.判定解的情况,单纯求r(A),r(A,b)的过程行列变换都可
注:将r(A,b)化行阶梯求秩时,往往我们需要同时得到r(A),如果想用列变换的话,只能对A单独列变换,千万不要将b列和A的列混合运算,这样r(A)就不准了。(但r(A,b)是准的)。

但是,如果涉及到求通解或唯一解,那么就只能做行变换化行阶梯了,所以建议一开始就只做行变换。
总结:求解的过程,就只进行初等行变换化行阶梯求秩,并且顺势化为行最简型求解。
5.求向量组极大无关组、线性表出关系,则仅行变换
因为初等行变换不改变列向量组的线性表出关系。例如下图,矩阵中,
,
矩阵同样有这样的关系。
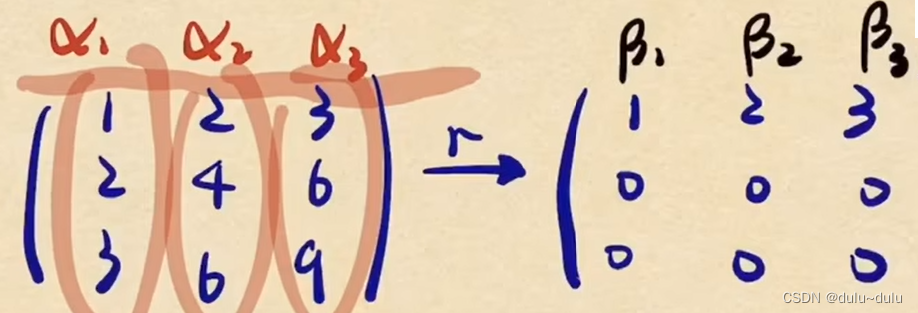
6.求向量组的秩时,行列变换都可
求向量组的秩,其实最后会转化为求矩阵的秩,原理就是"矩阵的秩=行向量组的秩=列向量组的秩",所以求向量组的秩也是行列变换都可。
![]()
但是一般求向量组的秩后面会继续求解极大无关组/线性表出关系,这时只能做行变换,所以还是建议从开头就只使用行变换。
7.求特征值时,行列变换都可
因为特征多项式本质上是行列式,求行列式时,行列都可以换。
![]()
8.求特征向量时,仅做行变换
因为求特征向量时,本质是在解线性方程组,只能进行初等行变换。

9.求逆矩阵时,对(A,E)仅做初等行变换
因为以左乘A得到E,以
左乘E得到
,以
左乘的过程就是做初等行变换的过程。

所以怎么体现A和E做了完全一样的所带来的初等行变换,就是将A,E横着拼在一起,此时做的初等行变换就是同步的了。
![]()
总结:
除了① 求行列式的值(求特征值本质上就是求行列式的值)和 ② 单纯求秩,行列变换都可,其余情况通通只做行变换。
二.要牢记

一些推导:

对于AB ≠ BA的补充:

三.某某子式
1.余子式
在n阶行列式中,去掉元素a所在的第i行、第j列元素,由剩下的元素按原来的位置与顺序组成的n-1阶行列式称为元素a的余子式,记作。
2.代数余子式
余子式乘
后称为a的代数余子式,记作A

3.k阶子式
给定一个矩阵,任取k行,任取k 列,共个数构成的行列式,出现在矩阵的秩中,定义如下:
设A是mxn矩阵,则若存在k阶子式不为零,而任意k+1阶子式(如果有的话)全为零,则r(A)=k,且若A为nxn矩阵,则:

4.k阶主子式
指在行列式中选k行k列,但要求行和列的下标相同。如:行为r1、r2、r3,列必须为c1、c2、c3;行为r2、r3、r5,列必须为c2、c3、c5。因此,k阶主子式不唯一。
这在矩阵相似会用到,下面会讲。
5.顺序主子式
顺序主子式是在主子式上再加限定,顺序主子式是由 1~k 行和 1~k 列所确定的子式。
例如:
1阶时:取第1行,第1列
2阶时:取第1、2行,第1、2列
3阶时:取第1、2、3行,第1、2、3列
4阶时:取第1、2、3、4行,第1、2、3、4列
实际上,主子式的主对角线元素是原 n 阶行列式的主对角线元素的一部分,且顺序相同。
所以k 阶主子式是不唯一的,而 k 阶顺序主子式是唯一的。
用在判断二次型正定上,下面会讲。
四.矩阵的秩
① 0 <= r(A) <= min{m,n}
② r(kA)=r(A)(k ≠ 0)
③ r(AB) <= min{r(A),r(B)}
④ r(A+B) <=r(A)+r(B)
⑤

r(A)=n-1,r(A*)=1的证明:

进而可得出一个重要结论:
,则r(A)+r(B)<=n
⑥ 设A是m*n矩阵,P,Q分别是m阶,n阶可逆矩阵,则
r(A)=r(PA)=r(AQ)=r(PAQ)
⑦ r(A)==r(
)=r(
)
五.常用特征值与特征向量

六
1.矩阵的逆
除了一般公式,矩阵的逆和伴随:
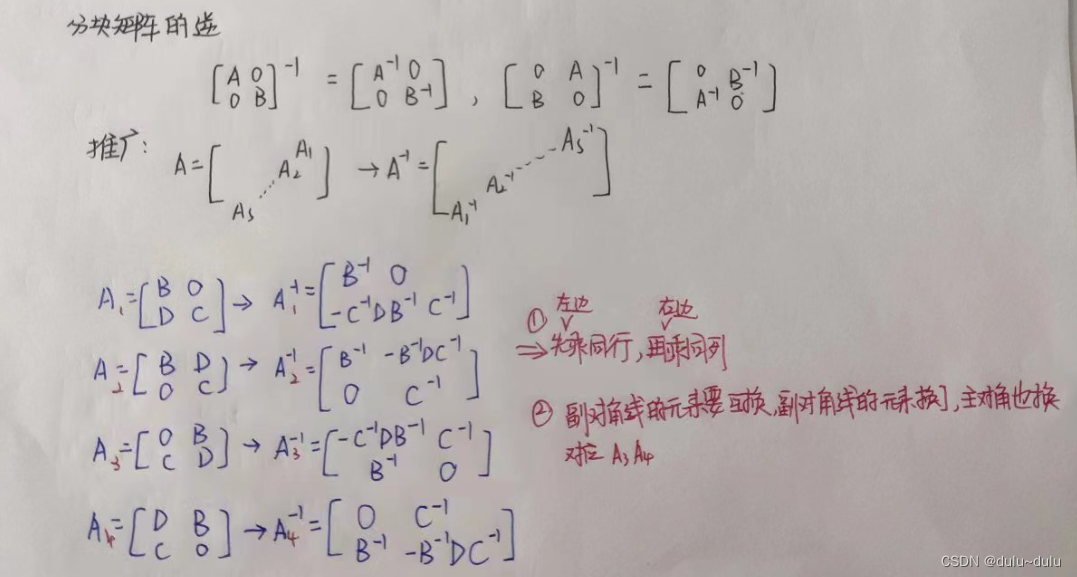
推导如下:

2.矩阵的伴随

六.矩阵,向量组,方程组
矩阵,向量组
① 向量组是由有限个相同维数的行向量或者列向量组成,其中向量是由n个实数组成的有序数组,是一个n*1的矩阵(n维列向量)或是一个1*n的矩阵(n维行向量)。
② 矩阵是由m*n个数排列成m行n列的数表。
一个向量组可以看作是一个矩阵的列(或行)向量集合。如果一个矩阵有n列,那么这n列就可以看作是一个由n个向量组成的向量组。反过来,一个矩阵也可以看作是由其列(或行)向量组成的向量组。
1.怎么判断两个矩阵等价
矩阵等价的前提:A与B是同型矩阵,即A,B行数,列数相同
矩阵等价的充要条件:
① r(A)=r(B)
② PAQ=B,P,Q可逆
2.怎么判断两个向量组是等价向量组
向量组等价的前提:A,B矩阵同维
若r( Ⅰ )=r(
....) r(Ⅱ)=r(
....)
向量组等价的充要条件:
① r(Ⅰ)=r(Ⅱ),且(Ⅰ)可由(Ⅱ)线性表出(单向表出即可)② r(Ⅱ)=r(Ⅰ),且(Ⅱ)可由(Ⅰ)线性表出(单向表出即可)
③ r(
....) =r(
....) =r(
...,
...),即
r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ)
④ Ⅰ和Ⅱ能够相互线性表示。
总结:
① 两个矩阵A与B等价指的是A可以通过有限次初等变换变成B。两个不同型矩阵是不可能等价
乡
② 两个向量组等价只指的是它们能够互相线性表示,它们各自所含向量的个数可能是不一样的。
例题:

D.即使Ⅰ 和 Ⅱ 同为n维向量组,但是s与t的关系未知,也就是行数相等,列数未知,所以A,B两个矩阵可能不同型,不能等价。
B.(Ⅰ)可由(Ⅱ)表示,缺少其他条件,如果① 加上(Ⅱ)可由(Ⅰ)线性表出 或者② r(Ⅰ)=r(Ⅱ)就对了
C正确
D r(A)=r(B),只能推出两个向量组秩相同,缺少其他条件,如果加上① 加上(Ⅱ)可由(Ⅰ)线性表出 或者②加上(Ⅰ )可由(Ⅱ)线性表出或者③ r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ),就对了。
3.同解方程组
若两个方程组与
有完全相同的解,则称它们为同解方程组
充要条件:
① Ax=0的解满足Bx=0,且Bx=0的解满足Ax=0(互相把解代入求出结果即可)
② r(A)=r(B),且Ax=0的解满足Bx=0(或Bx=0的解满足Ax=0)
③ r(A)=r(B)=r(
)(三秩相同)
例1:

例2:

七.齐次线性方程组和非齐次线性方程组
齐次线性方程组有解的条件:
① r(A)=n时,方程组有唯一零解。
② r(A)=r<n时,方程组有非零解(无穷多解),且有n-r个线性无关解
齐次方程组其实就是解和系数的正交,例如,给你一个条件:
---->
则(1 -2 -1 0)就是齐次方程组的基础解系
非齐次线性无关组有解的条件:
① 若r(4)≠r([A,b]),则方程组无解;
② 若r(A)=r([A,b])=n,则方程组有唯一解;
③ r(A)=r([A,b])=r<n,则方程组有无穷多解。
非齐次方程组的通解的求法:
①求Ax=0的解
② 求Ax=b的一个特解
③ 非齐次方程组的通解=齐次方程组的解+一个非齐次的特解

如果A行满秩,则r(A)=r(A|b),那么方程组一定有解。
如果A列满秩,则r(A)与r(A|b)的关系不确定:
① r(A)<r(A|b),则无解
② r(A)=r(A|b)<n,有无穷多解
③ r(A)=r(A|b)=n,有唯一解
八.对比记忆
1.
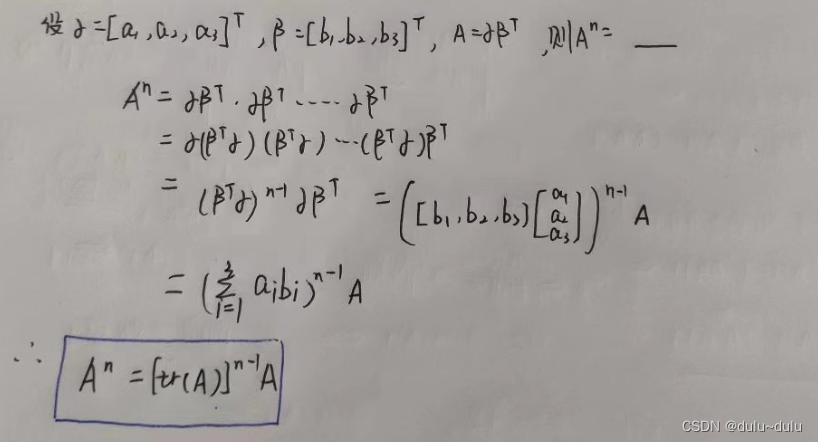
矩阵A的tr(A):tra(A)=矩阵A的迹=对角线元素之和
2.对于秩为1的n阶矩阵A或A=(或
)(a,β都是n维非零列向量),其特征值为
=0,
(或
)

3.

例题1:

例题2:

九.相似与正交
存在n阶可逆矩阵P,使得,则称A相似于B,记为A~B
若A~B
① |A|=|B|
② r(A)=r(B)
③ tr(A)=tr(B)
④
(
)
⑤
⑥ A,B各阶主子式之和分别相同

那么怎么判定矩阵相似呢?
① 定义法
存在n阶可逆矩阵P,使得
② 传递法
A~
,
~B,则A~B,其中
为对角阵
这就要说到矩阵的相似对角化
矩阵可相似对角化的条件:
充要条件:
① n阶矩阵A可相似对角化↔有n个线性无关的特征向量。
② n阶矩阵A可相似对角化↔A对应于每个k重特征值都有k个线性无关的特征向量
必要条件:
③ n阶矩阵A有n个不同特征值→A可相似对角化
④ n阶矩阵为实对称矩阵→A可相似对角化
对于矩阵相似对角化的步骤:
① 求特征值
② 求特征向量
③ 正交化(如果需要的话),单位化
④ 令Q=[
],则Q为正交矩阵,且
上面提到了实对称矩阵,实对称矩阵就是组成A的元素都是实数。对于实对称矩阵()要记住:

对于正交,你需要记住:
①,则
,
是正交向量
② 若满足
,则A是正交矩阵
↔
例题:

矩阵相似还可得出:
① A~B,
,f(A)=f(B)
② 若A~B,且A可逆,则
~
,f(
)=f(
)
③ 若A~B,
~
④ 若A~B,
~
注:
十.合同
设A,B为n阶矩阵,若存在可逆矩阵C,使得,则称A与B合同,即
。A与B合同,就是指同一个二次型在可逆线性变换下的两个不同状态的联系。
A与B合同的充要条件:正惯性性指数(p)等于负惯性指数(q)
① pA=PB,且qA=qB
② pA=PB,且r(A)=r(B)
③ qA=qB,且r(A)=r(B)
注:由于我们已经规定,对称矩阵才是二次型矩阵,所以二次型矩阵都是对称矩阵,相应的和对称矩阵合同的矩阵也是对称矩阵。
十一.二次型
关于二次型化标准型或规范型的方法:配方法,正交变化有总结如下:

这里记录一个例题:


十二.二次型正定
二次型正定的充要条件:
n元二次型正定↔对任意x≠0,有
>0(定义)
① ↔f的正惯性指数p=n
② ↔存在可逆矩阵D,使得
③ ↔
,A与E合同
② ③推导:
④↔A的特征值
>0
⑤↔A的全部顺序主子式>0
二次型正定的必要条件:
①
>0,对角线元素全部大于0
② |A|>0
最好是使用充要条件① ④ ⑤判断二次型是否正定,如果非要用定义法,来看个例题:

注意上题,不能直接将f判定为正定:
因为将二次型化为标准型的过程一定要做可逆线性变换

例题:


有错欢迎评论区指正!❤️❤️❤️
相关文章:

线代知识点总结
目录 一.初等行/列变换 1.计算行列式时,行列变换都可 2.求矩阵的秩时,行列变换都可 3.解线性方程组时,仅能使用初等行变换 4.判定解的情况,单纯求r(A),r(A,b)的过程行列变换都可 5.求向量组极大无关组、线性表出关系&#x…...
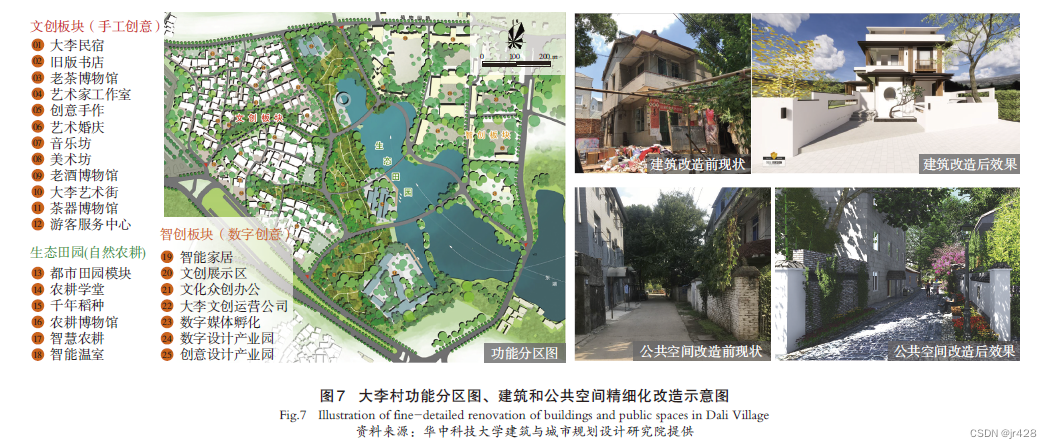
案例学习-存量更新规划实施探索(武汉)
案例学习-存量更新规划实施探索(武汉) 武汉市在早期旧城更新实践中发现零散化的更新往往导致资源配置分散、城市建设破碎化等弊病,特别是由于过于强调项目自身“经济平衡”,在实施过程中也逐步暴露出住宅占比过大、强度偏高、公服…...
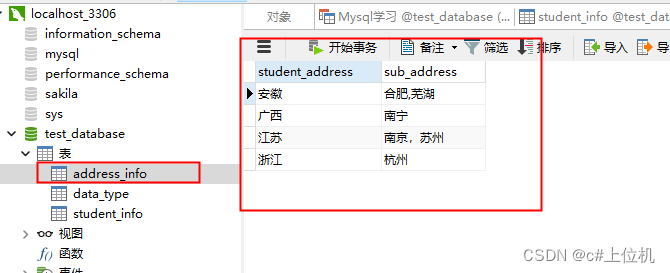
C#操作MySQL从入门到精通(17)——使用联结
前言: 我们在查询数据的过程中有时候查询的数据不是来自一个表而是来自多个表,本文使用的测试数据如下: 本文使用了两个表student_info、address_info student_info的数据如下: address_info的数据如下: 1、内联结 所谓内联结就是求交集,两个表都有的数据才是有效数…...

MyBatis 关于查询语句上配置的详细内容
1. MyBatis 关于查询语句上配置的详细内容 文章目录 1. MyBatis 关于查询语句上配置的详细内容2. 准备工作3. SQL查询结果,返回为POJO实体类型4. SQL查询结果,返回为List<POJO\> 集合类型5. SQL查询结果,返回为Map 集合6. SQL查询结果&…...
基于STM32和人工智能的智能家居监控系统
目录 引言环境准备智能家居监控系统基础代码实现:实现智能家居监控系统 4.1 数据采集模块4.2 数据处理与分析4.3 控制系统4.4 用户界面与数据可视化应用场景:智能家居管理与优化问题解决方案与优化收尾与总结 1. 引言 随着智能家居技术的快速发展&…...
这三款使用的视频、图片设计工具,提供工作效率
Videograp Videograp是一款专注于视频生成的工具,特别适合需要快速剪辑和编辑视频的用户。Videograp具备以下特点: 影音比例转换:Videograp支持调整视频的分辨率和比例,使其更适合不同的播放环境和设备。 AI快剪:该工…...
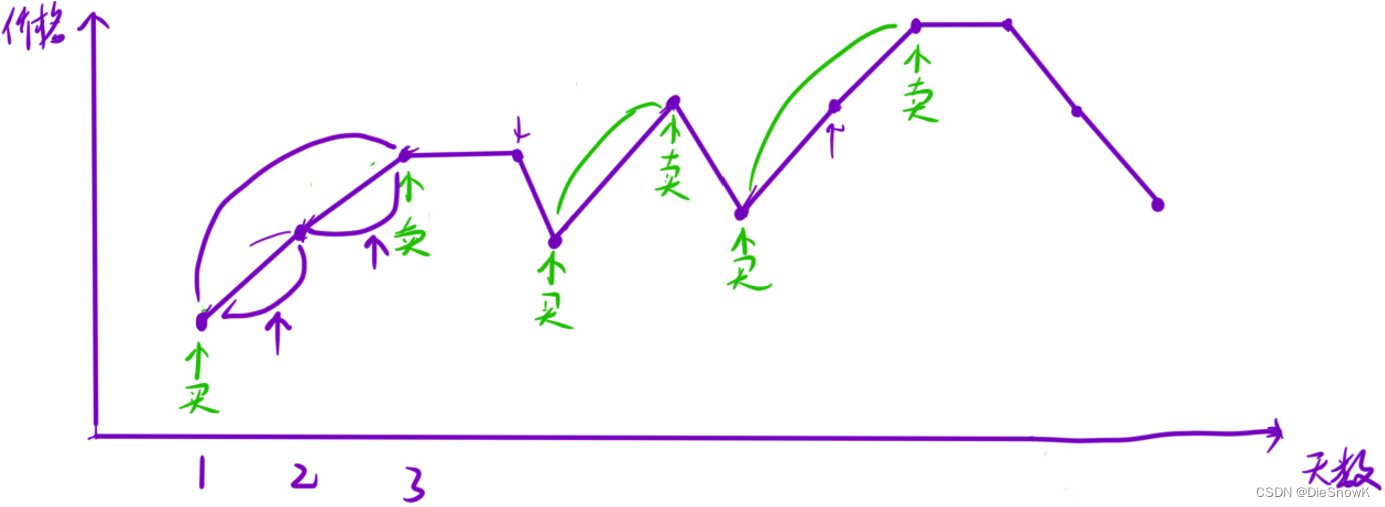
[Algorithm][贪心][最长递增子序列][递增的三元子序列][最长连续递增序列][买卖股票的最佳时机][买卖股票的最佳时机Ⅱ]详细讲解
目录 1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.递增的三元子序列1.题目链接2.算法原理详解3.题目链接 3.最长连续递增序列1.题目链接2.算法原理详解3.代码实现 4.买卖股票的最佳时机1.题目链接2.算法原理详解3.代码实现 5.买卖股票的最佳时机 II1.题目链接2.算法…...

手把手教你入门vue+springboot开发(三)--登录功能后端
文章目录 前言一、redis安装二、后端代码1.修改application.yml文件2.增加utils文件3.增加Result类4.修改UserController类5.修改UserMapper类6.修改UserService和UserServiceImpl类7.增加LoginInterceptor类8.增加WebConfig类9.修改pom.xml文件 前言 前两篇我们用vuespringbo…...
三款有3D效果的js图表库
1、G2简洁的渐进式可视化语法。https://g2.antv.antgroup.com/manual/extra-topics/3d-charts 2、 https://www.highcharts.com/https://www.highcharts.com/ 3、https://www.fusioncharts.com/charts/pie-doughnut-charts/donut-chart-in-3d?frameworkjavascripthttps://www…...

【SQLAlChemy】表之间的关系,外键如何使用?
表之间的关系 数据库表之间的关系分为三种: 一对一关系(One-to-One):在这种关系中,表A的每一行都与表B的一行关联,反之亦然。例如,每个人都有一个唯一的社保号,每个社保号也只属于…...

Linux 基础IO 二
1.文件描述符的分配规则 #include<stdio.h> #include<string.h> //#include<unistd.h> #include<sys/types.h> #include<sys/stat.h> #include<fcntl.h>int main() {close(1);//fd分配原则,从最小的开始,没有被占用…...

找工作小项目:day15-macOS支持、完善逻辑
macOS支持、完善逻辑 目前的代码可以在Linux上完美运行编译,在Windows上也可以通过WSL编译运行源代码,但是在MacBook上却无法运行编译,这主要是由于macOS上没有epoll,取而代之的很相似的kqueue。由于操作系统不同,我们…...
植物大战僵尸杂交版 v2.0.88 mac版 Plants vs. Zombies 杂交版下载
特别注意:该游戏最低系统要求为macOS Sonoma 14.X,低于此系统版本的请勿下载! 游戏介绍 植物大战僵尸杂交版是由B站UP主“潜艇伟伟迷”制作的一款结合了《植物大战僵尸》原有元素与创新玩法的游戏。这款游戏以其独特的“杂交”植物概念在B站…...

PHP中的while循环:用法、技巧与最佳实践
在PHP编程中,while循环是一种基本且常用的控制结构,用于重复执行代码块,直到指定条件为假。while循环在处理未知迭代次数的任务时特别有用,例如读取文件内容、处理用户输入或动态生成数据等。与for循环不同,while循环适…...

如何解决跨境传输常见的安全及效率问题?
在当今全球化的商业版图中,企业为了拓展国际市场和增强竞争力,跨境传输数据已成为一项不可或缺的业务活动。合格的数据跨境传输方案,应考虑以下要素: 法律合规性:确保方案符合所有相关国家的数据保护法律和国际法规&am…...

『大模型笔记』主成分分析(PCA)解释:简化机器学习中的复杂数据!
主成分分析(PCA)解释:简化机器学习中的复杂数据 文章目录 一. 主成分分析(PCA)解释:简化机器学习中的复杂数据!二. 参考文献一. 主成分分析(PCA)解释:简化机器学习中的复杂数据! 主成分分析(Principal Component Analysis,简称PCA)通过 将大型数据集中的维度减少…...

springboot与flowable(5):任务分配(表达式)
在做流程定义时我们需要给相关的用户节点指派对应的处理人。在flowable中提供了三种分配的方式。 一、固定分配 在分配用户时选择固定值选项确认即可。 二、表达式 1、值表达式 2、方法表达式 三、表达式流程图测试 1、导出并部署 导出流程图,复制到项目中 部署流…...
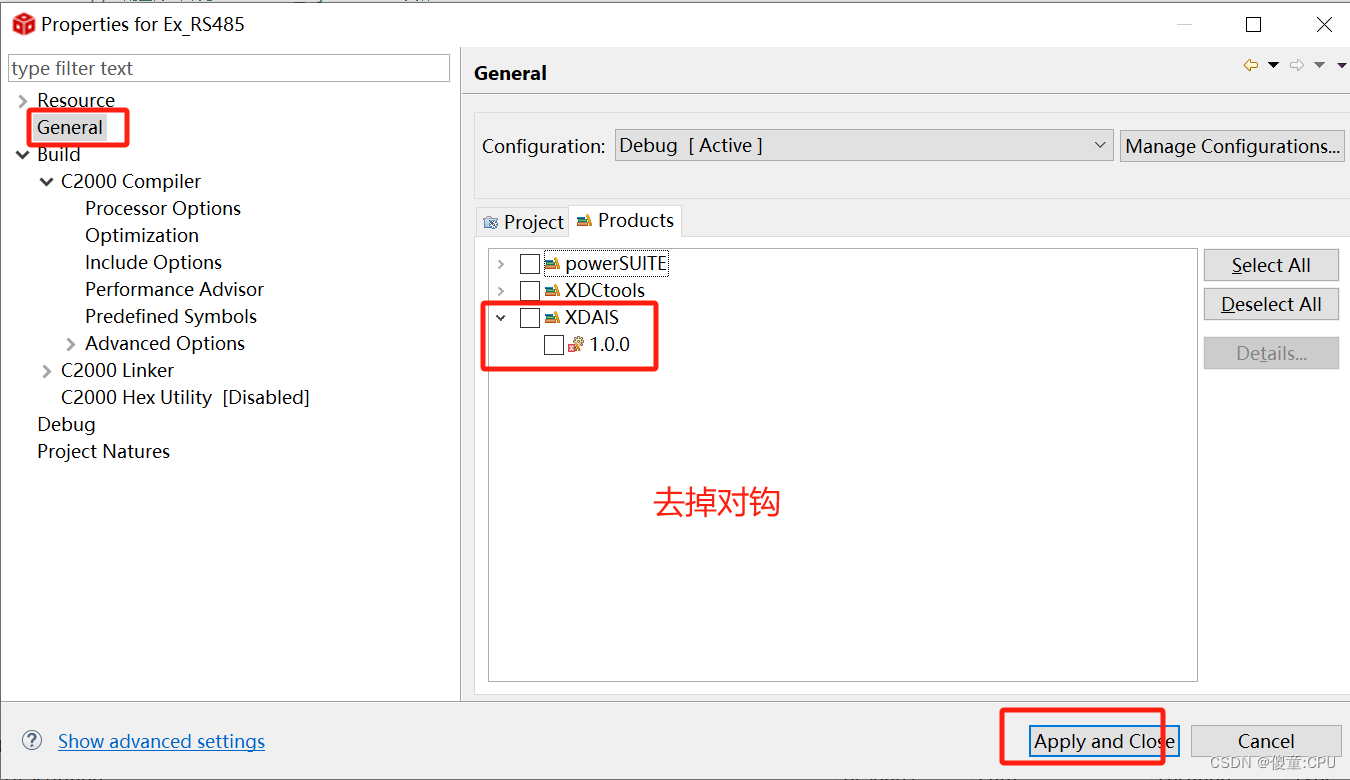
如何使用CCS9.3打开CCS3.0工程
如何使用CCS9.3打开CCS3.0工程 点菜单栏上的project,选择Import Legacy CCSv3.3 Porjects…,弹出对话框,通过Browse…按钮导入一个3.3版本的工程项目; 选择.pjt文件,选择Copy projects into worlkspace 右击选择P…...

Stable Diffusion 3 Medium 模型
开源SD3,中型版本,20亿参数,Stable Diffusion 3 Medium,系统内存要求32G,显卡6G。 a female character with long, flowing hair that appears to be made of ethereal, swirling patterns resembling the Northern Li…...
)
数据分析------统计学知识点(五)
回归算法 想象一下,你和朋友在讨论:大学生活中,每天学习的时间是否真的能影响期末成绩?这个问题看似简单,实则包含了一个潜在的关系:学习时间与成绩之间的联系。我们想要知道,增加学习时间是否会提高成绩,以及这种提…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...





