Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式
Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式

拷贝后, 所有账户和数据都是一样的
步骤
- 停止MySQL服务
net stop mysql或sc.exe stop mysql
net stop mysql
sc.exe stop mysql
- 卸载 Mysql8.3.0 的服务
mysqld remove或mysqld remove mysql
用mysql-8.3.0-winx64/bin/的mysqld.exe执行, 配置环境变量,或进入对应版本bin文件夹./mysqld
mysqld remove
mysqld remove mysql
-
拷贝
mysql-8.3.0-winx64/data文件夹到mysql-8.4.0-winx64/data -
更换环境变量, 也可以不用环境变量,每次都到对应目录或全路径执行命令
-
用
mysql-8.4.0-winx64/bin/的mysqld.exe执行mysqld insatll或mysqld install mysql安装服务
mysqld install
mysqld install mysql
- 启动 mysql 服务
net start mysql或sc.exe start mysql
net start mysql
sc.exe start mysql
相关文章:

Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式
Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式 拷贝后, 所有账户和数据都是一样的 步骤 停止MySQL服务 net stop mysql 或 sc.exe stop mysql net stop mysqlsc.exe stop mysql卸载 Mysql8.3.0 的服务 mysqld remove 或 mysqld remove m…...
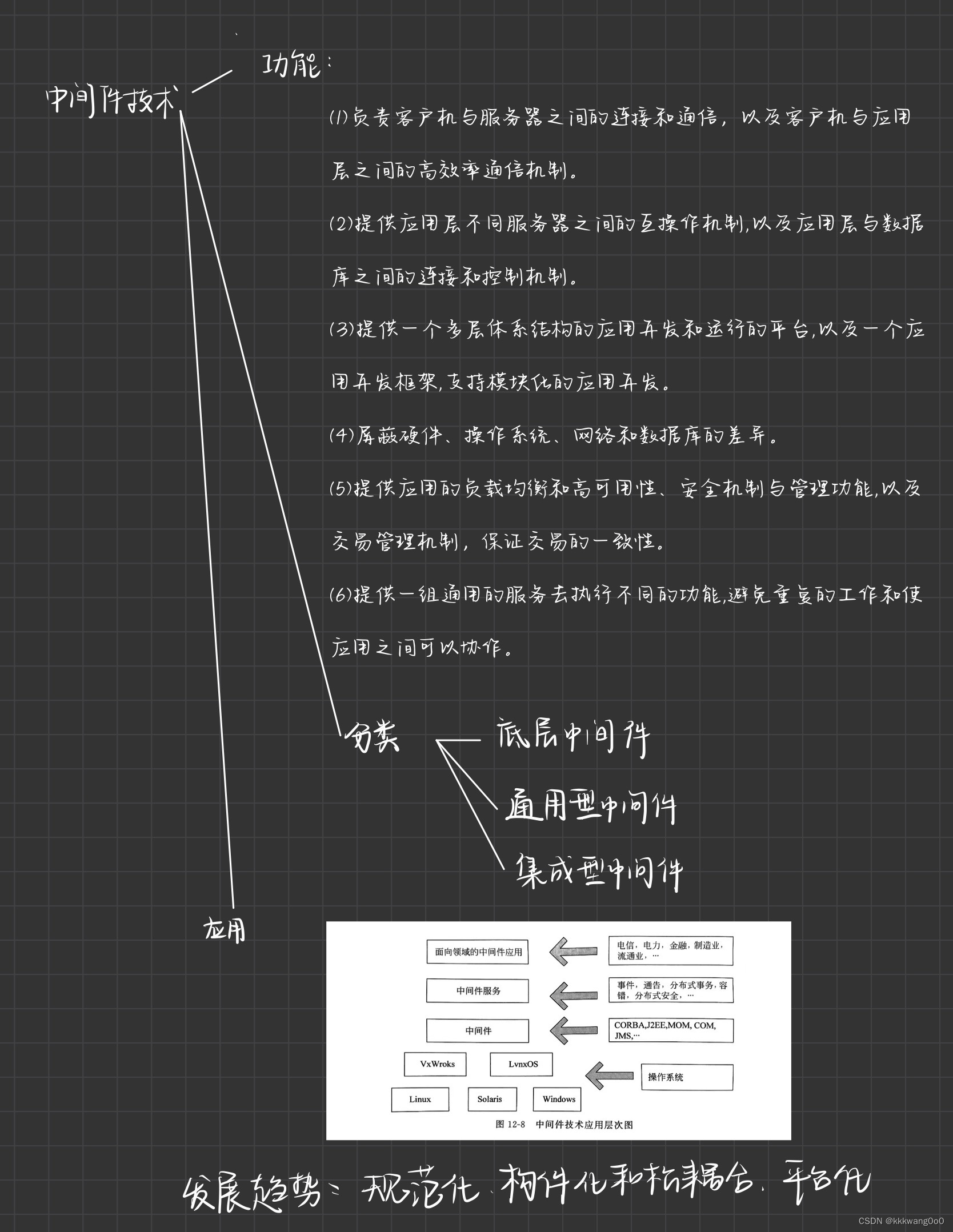
软件体系结构笔记(自用)
来自《软件体系结构原理、方法与实践(第三版)》清华大学出版社 张友生编著 1-8章12章 复习笔记 如有错误,欢迎指正!!!...

java安装并配置环境
安装前请确保本机没有java的残留,否则将会安装报错 1.安装java jdk:安装路径Java Downloads | Oracle 中国 百度网盘链接:https://pan.baidu.com/s/11-3f2QEquIG3JYw4syklmQ 提取码:518e 2.双击 按照流程直接点击下一步&#x…...
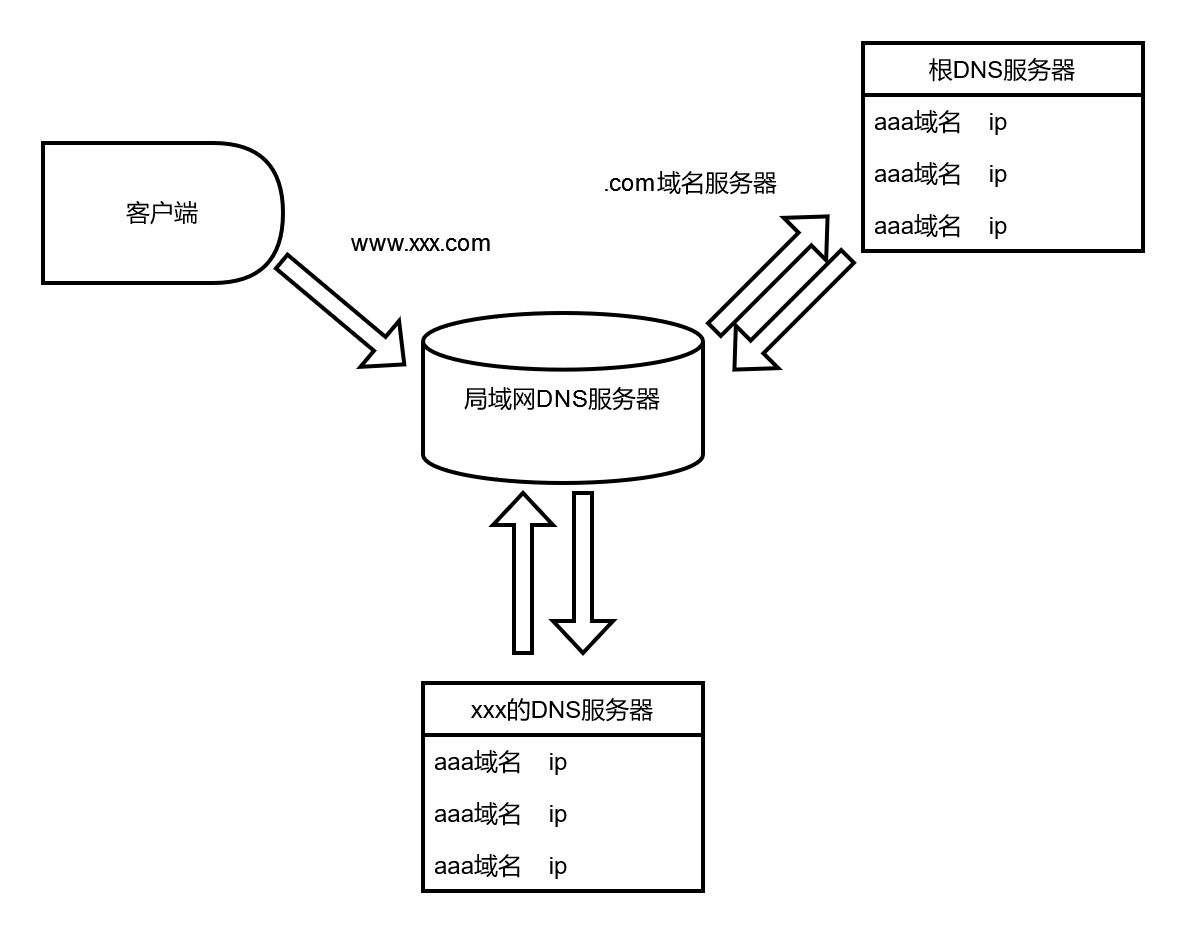
探索互联网寻址机制 | 揭秘互联网技术的核心,解析网络寻址
揭秘互联网技术的核心,解析网络寻址题 前提介绍局域网地址IP地址的分配方式动态IP分配机制内部网(intranet)ICANN负责IP分配DHCP协议获取IP地址 域名系统域名是什么域名工作方式hosts文件存储域名映射关系DNS分布式数据库DNS域名解析 Java进行…...
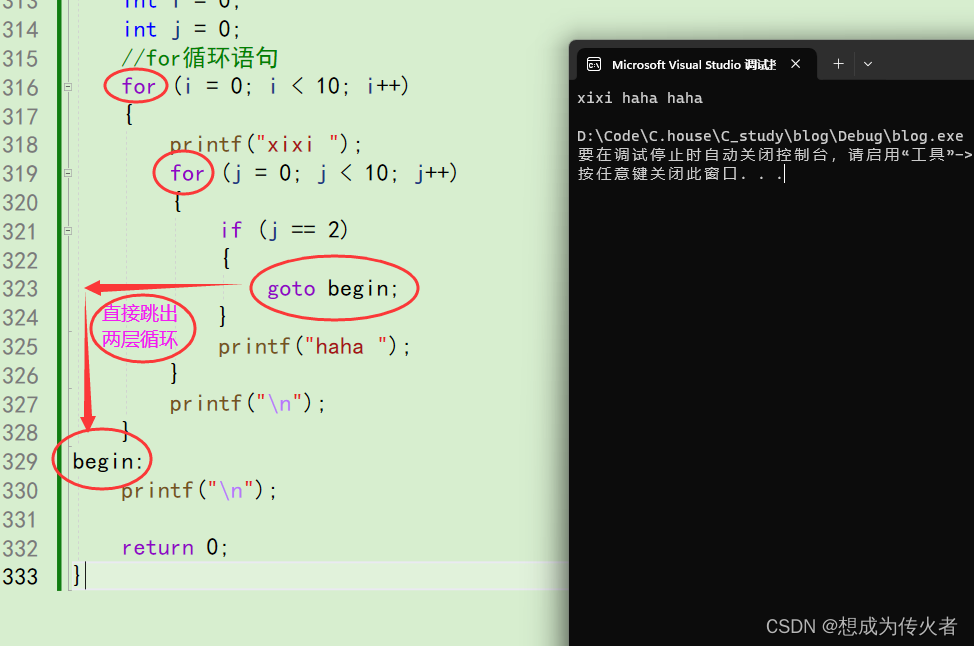
C语言学习笔记之结构篇
C语言是一门结构化程序设计语言。在C语言看来,现实生活中的任何事情都可看作是三大结构或者三大结构的组合的抽象,即顺序,分支(选择),循环。 所谓顺序就是一条路走到黑;生活中在很多事情上我们都…...

C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法
C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法 —— 2024-06-08 杭州 code review! 文章目录 C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法一.从一个函数中获取多个返回值的方法1. 使用结构体或类2. 使用`std::t…...

GDB:从零开始入门GDB
目录 1.前言 2.开启项目报错 3.GDB的进入和退出 4.GDB调试中查看代码和切换文件 5.GDB调试中程序的启动和main函数传参 6.GDB中断点相关的操作 7.GDB中的调试输出指令 8.GDB中自动输出值指令 9.GDB中的调试指令 前言 在日常开发中,调试是我们必不可少的技能。在专业…...

服务器权限管理
我们linux服务器上有严格的权限等级,如果权限过高导致误操作会增加服务器的风险。所以对于了解linux系统中的各种权限及要给用户,服务等分配合理的权限十分重要。(权限越大,责任越大) 1.基本权限 U--user用户,G-group…...

08 SpringBoot 自定定义配置
SpringBoot自定义配置有三种方式: 使用PropertySource进行自定义配置 使用ImportResource进行自定义配置 使用Configuration进行自定义配置 PropertySource 如果将所有的配置都集中到 application.properties 或 application.yml 中,那么这个配置文…...
加密计算(DESede/ECB/ZeroPadding))
Java之3DES(Triple DES)加密计算(DESede/ECB/ZeroPadding)
Java环境本身并不直接支持DESede/ECB/ZeroPadding。 不过,可以通过以下几种方式来实现DESede/ECB/ZeroPadding: 手动实现填充和去除填充:如前面示例代码所示,在加密之前进行填充,在解密之后去除填充。这是一个通用的方…...

从0开发一个Chrome插件:项目实战——广告拦截插件
前言 这是《从0开发一个Chrome插件》系列的第十七篇文章,本系列教你如何从0去开发一个Chrome插件,每篇文章都会好好打磨,写清楚我在开发过程遇到的问题,还有开发经验和技巧。 专栏: 从0开发一个Chrome插件:什么是Chrome插件?从0开发一个Chrome插件:开发Chrome插件的必…...

C++ 32 之 静态成员函数
#include <iostream> #include <string> using namespace std;// 特点: // 1.在编译阶段就分配了内存空间 // 2.类内声明,在类外进行初始化 // 3.所有对象共享一份静态成员数据 class Students02{ public:int s_c;static int s_d;// 静态成员函数&#…...

Python闯LeetCode--第1题:两数之和
Problem: 1. 两数之和 文章目录 思路解题方法复杂度Code 思路 看到这道题第一思路就是暴力破解,枚举,两个for循环遍历,直到找到满足要求的答案。主要因题目假设只有一组满足结果的答案,因此难度大大降低,作为第一道题&…...

SSM情侣购物系统-计算机毕业设计源码02387
目 录 摘要 1 绪论 1.1 开发背景与意义 1.2开发意义 1.3Vue.js 主要功能 1.3论文结构与章节安排 2 情侣购物系统系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据流程 3.3.2 业务流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系统用例分…...

09-Spark架构
相比MapReduce僵化的Map与Reduce分阶段计算,Spark计算框架更有弹性和灵活性,运行性能更佳。 1 Spark的计算阶段 MapReduce一个应用一次只运行一个map和一个reduceSpark可根据应用复杂度,分割成更多的计算阶段(stage)…...

挑战5分钟内基于Springboot+SpringMVC+Mybatis-plus快速构建web后端三层架构
目标 在清晨的代码编辑器上,一场新的挑战即将开始。程序员们肃立于安静的办公室,眼神专注地盯着屏幕,等待着编译器的一声提示。 随着编译器输出的激动人心的"start!"的提示,战斗的序幕拉开了。Bug如潮水般涌来&#x…...

浅谈JavaScript中的作用域
前言 今天就来简单聊聊JavaScript中的作用域吧!!! 正文 我们都知道,在任何一门编程语言里面都是有作用域这个概念的,不然岂不乱套了 在js中的作用域一共分为三种,全局域、函数域和块级作用域 全局域 全…...

Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点 🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分…...

python如何对list求和
如何在Python中对多个list的对应元素求和,前提是每个list的长度一样。比如:a[1,2,3],b[2,3,4],c[3,4,5],对a,b,c的对应元素…...
如何解决mfc100u.dll丢失问题,关于mfc100u.dll丢失的多种解决方法
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“计算显示缺失mfc100u.dll”。这个问题可能会影响到我们的正常使用,因此了解它的原因、表现以及解决方法是非常重要的。小编将详细介绍计算显示缺失mfc100u.dll的问题࿰…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
