专项攻克——二叉树

一、二叉树定义、分类

1. 二叉树：是N个结点的有序集合，该集合或者为空集，或者由一个根节点跟两棵互不相交的、分别称为根节点的左子树或者右子树的二叉树组成。每个结点最多有两个子树。左子树跟右子树是有序的。
2. 满二叉树：二叉树深度为k (k≥1)时，第k层有2^(k-1)个节点，二叉树总共有 。
3. 完全二叉树:只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。具有n个节点的完全二叉树的深度为： (log2n)+1 或 log2(n+1)

二叉树的特点：

• 在k层中的最大节点个数为 2^(k-1);
• 层数为k的树的最大节点个数为 2^k - 1;
• 叶节点的个数比度数为2的节点的个数要多1个: n0 = n2+1
• 总节点数为各类节点之和:n=no+n1+n2
• 总节点数为所有子节点数加一: n= n + 2*n2+ 1 故得: no=n2+1

二、二叉树的存储结构

以二叉链表存储为例

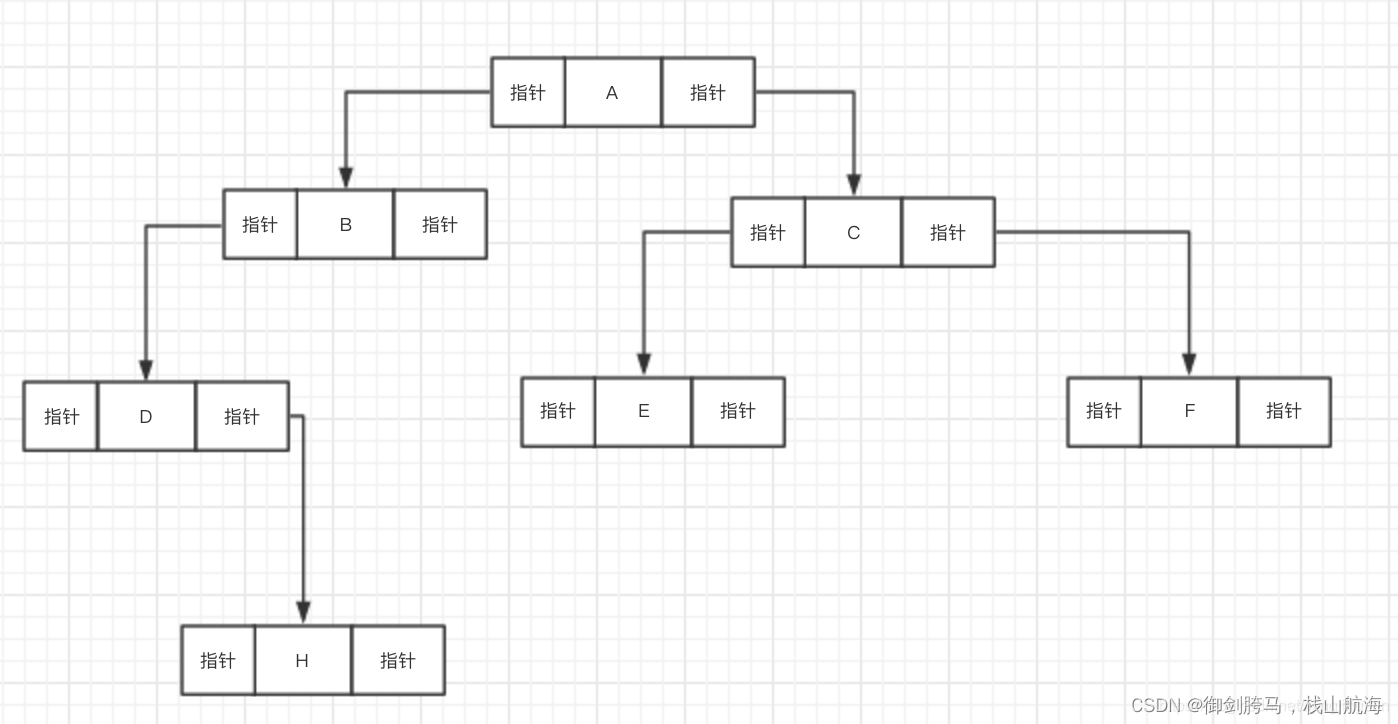
结构：

public class BinaryNode {//左节点public BinaryNode left;//数据域public int data;//右节点public BinaryNode right;public BinaryNode() {}public BinaryNode(int data) {this.data = data;}
}

三、创建二叉树

思路：相当于插入一系列值到空二叉树中，插入规则为

1. 当前值如果小于当下节点值：left非空则直接把值放入left，否则把left当成当下节点 继续递归。
2. 当前值如果大于当下节点值：right非空则直接把值放入right，否则把right当成当下节点 继续递归。

public class BinaryTree<V> {//根节点,默认为nullprivate BinaryNode root = null;/*** 描述: 构建二叉树* Node：节点,* data：待插入的数据*/private void buildBinaryTree(BinaryNode node, int data) {if (root == null) {root = new BinaryNode(data);return;}//根节点不为空,那么判断数据是否小于当前节点的数据if (data < node.data) {//如果小于,判断当前节点是否有左叶子节点if (node.left == null) {//左叶子节点为空,设置左叶子节点,并且设置数据node.left = new BinaryNode(data);} else {//左叶子节点不为空,递归调用构建二叉树的函数this.buildBinaryTree(node.left, data);}} else {//如果大于或等于,判断当前节点是否存在右叶子节点if (node.right == null) {//右叶子节点为空,设置右叶子节点,并且设置数据域node.right = new BinaryNode(data);} else {//右叶子节点点不为空,递归调用构建二叉树的函数this.buildBinaryTree(node.right, data);}}}/*** 前序遍历*/public void preOrder(BinaryNode node) {System.out.println(node.data);if (node.left != null) {this.midOrder(node.left);}if (node.right != null) {this.midOrder(node.right);}}/*** 中序遍历* */public void midOrder(BinaryNode node) {if (node.left != null) {this.midOrder(node.left);}System.out.println(node.data);if (node.right != null) {this.midOrder(node.right);}}/*** 后序遍历*/public void afterOrder(BinaryNode node) {if (node.left != null) {this.midOrder(node.left);}if (node.right != null) {this.midOrder(node.right);}System.out.println(node.data);}public static BinaryTree createBinaryTree(int[] datas) {BinaryTree binaryTree = new BinaryTree();for (int data : datas) {binaryTree.buildBinaryTree(binaryTree.root, data);}return binaryTree;}/*** 描述: 创建二叉树函数* int[] 是个int类型的数组* 通过循环调用,往二叉树插入数据*/public static void main(String[] arg) {int[] datas = new int[]{1, 9, 8, 2, 10};//构建二叉树BinaryTree binaryTree = createBinaryTree(datas);//前序遍历System.out.println("前序遍历");binaryTree.preOrder(binaryTree.root);//中序遍历System.out.println("中序遍历");binaryTree.midOrder(binaryTree.root);//后续遍历System.out.println("后序遍历");binaryTree.afterOrder(binaryTree.root);}
}

四、遍历方式

总结：通过看父节点的输出先后顺序，就可以判断是什么遍历方式。

分为三种遍历：

1. 前序遍历：先输出父节点， 再遍历左子树和右子树。
2. 中序遍历：先遍历左子树， 再输出父节点， 再遍历右子树。
3. 后序遍历：先遍历左子树， 再遍历右子树， 最后输出父节点。