SVM支持向量机
SVM的由来和概念

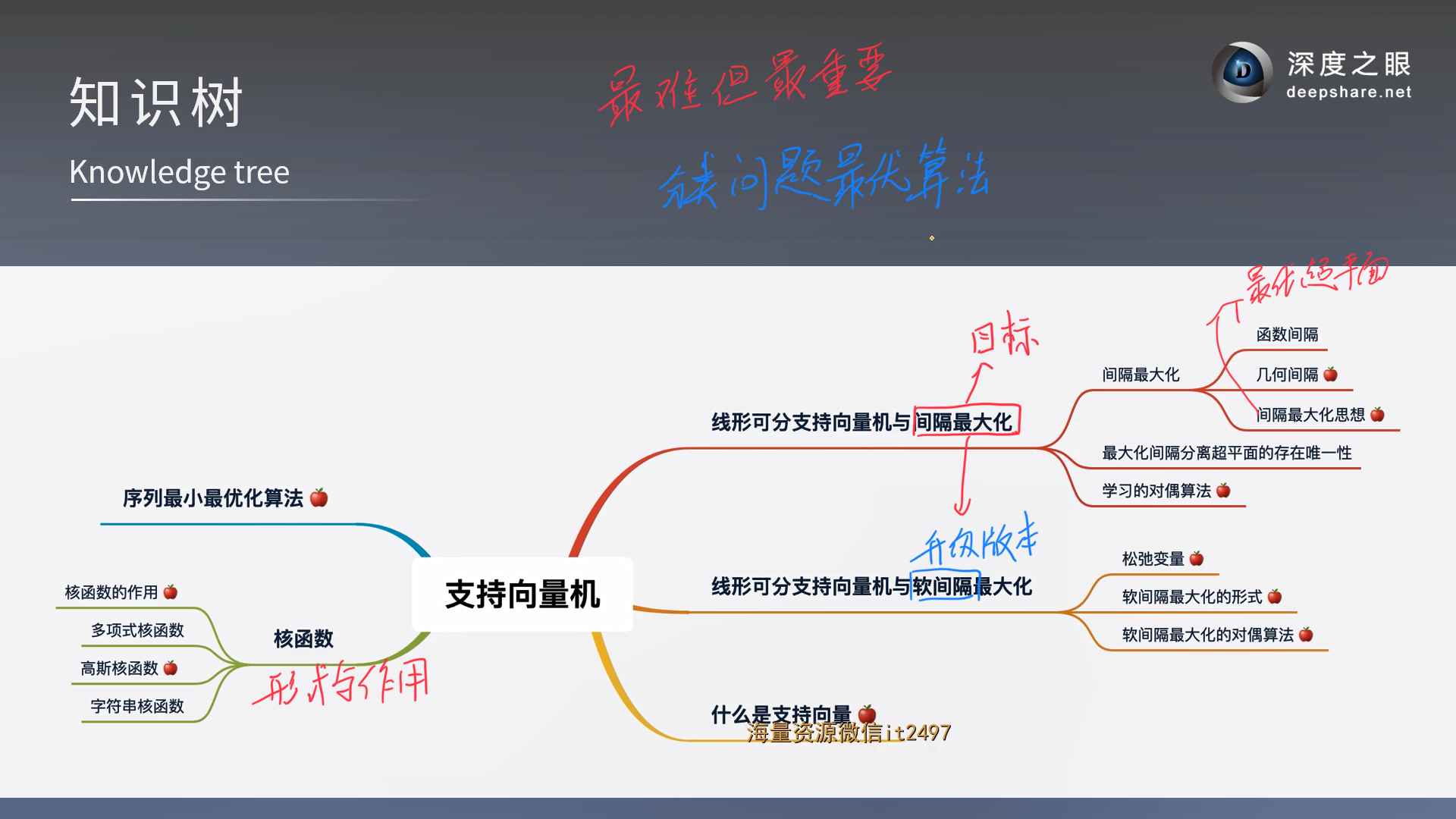


间隔最大化是找最近的那个点的距离’
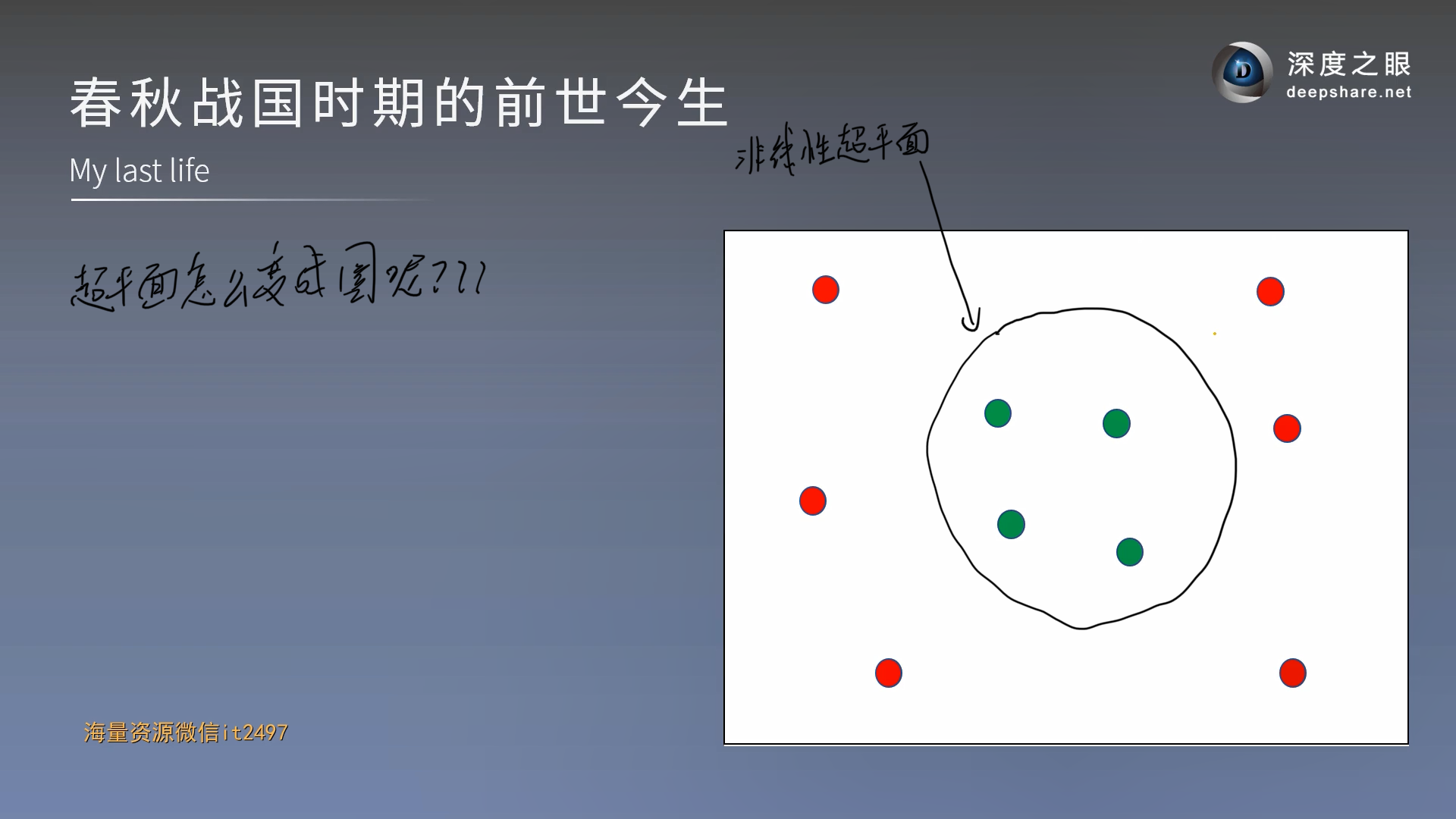
之前我们学习的都是线性超平面,现在我们要将超平面变成圈

对于非线性问题升维来解决
 对于下图很难处理,我们可以将棍子立起来,然后说不定red跑到左边了,green跑到右边了(可能增加了某种筛选条件导致两个豆子分离)(只是一种比喻)
对于下图很难处理,我们可以将棍子立起来,然后说不定red跑到左边了,green跑到右边了(可能增加了某种筛选条件导致两个豆子分离)(只是一种比喻)
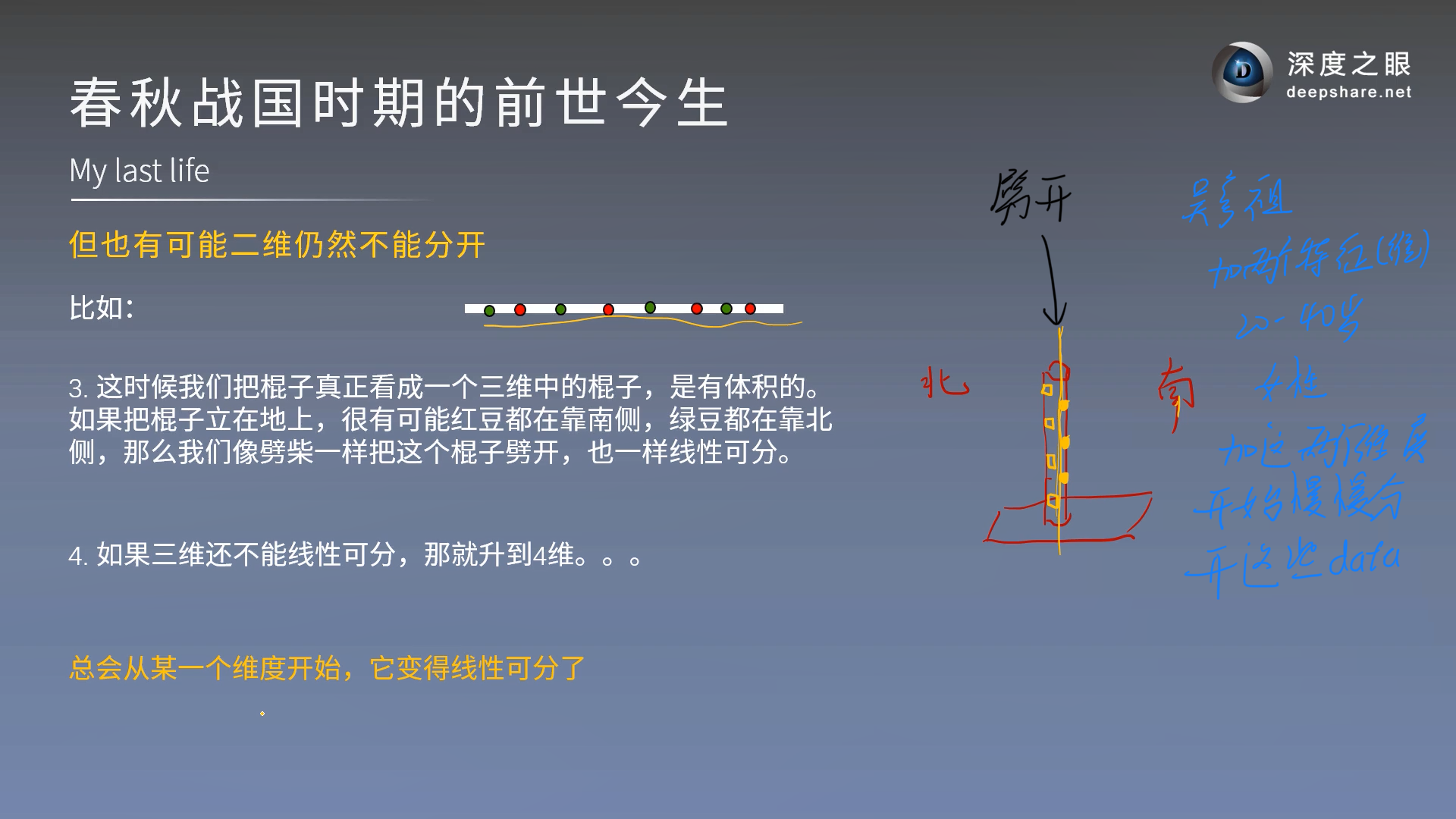
打个比方,要把刀哥和吴彦祖分开,豆子代表人们,加上几个特征(维度)1.20-40岁 2.女性 就可以大致将人们分的差不多了,可以继续加特征(维度)来使其更加分离
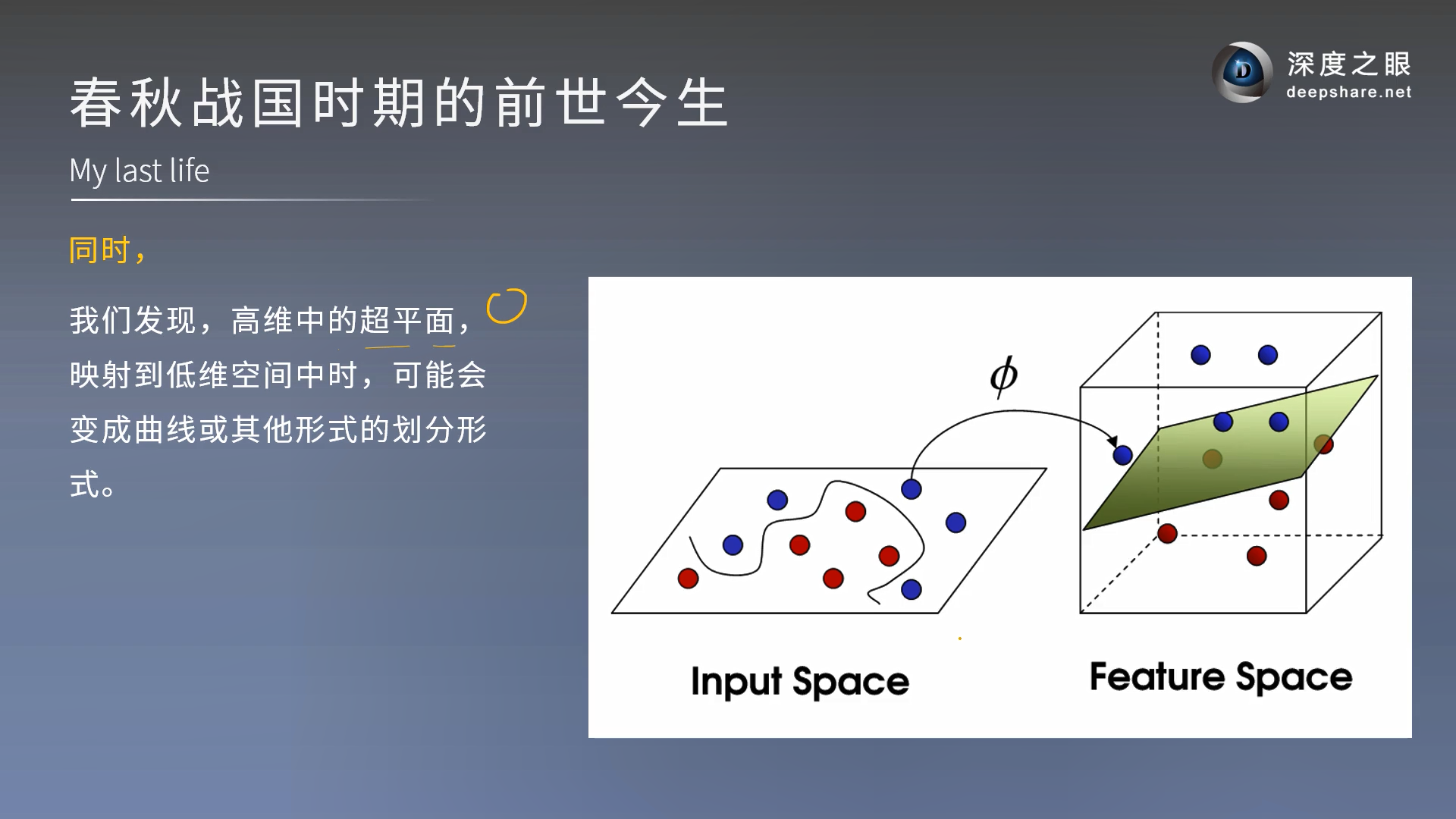

SVM本质还是非线性的,只是为了更好理解所以我们说在更高维是线性的


已经分开了,在再加特征(维度),相当于如虎添翼

复习函数间隔和几何间隔
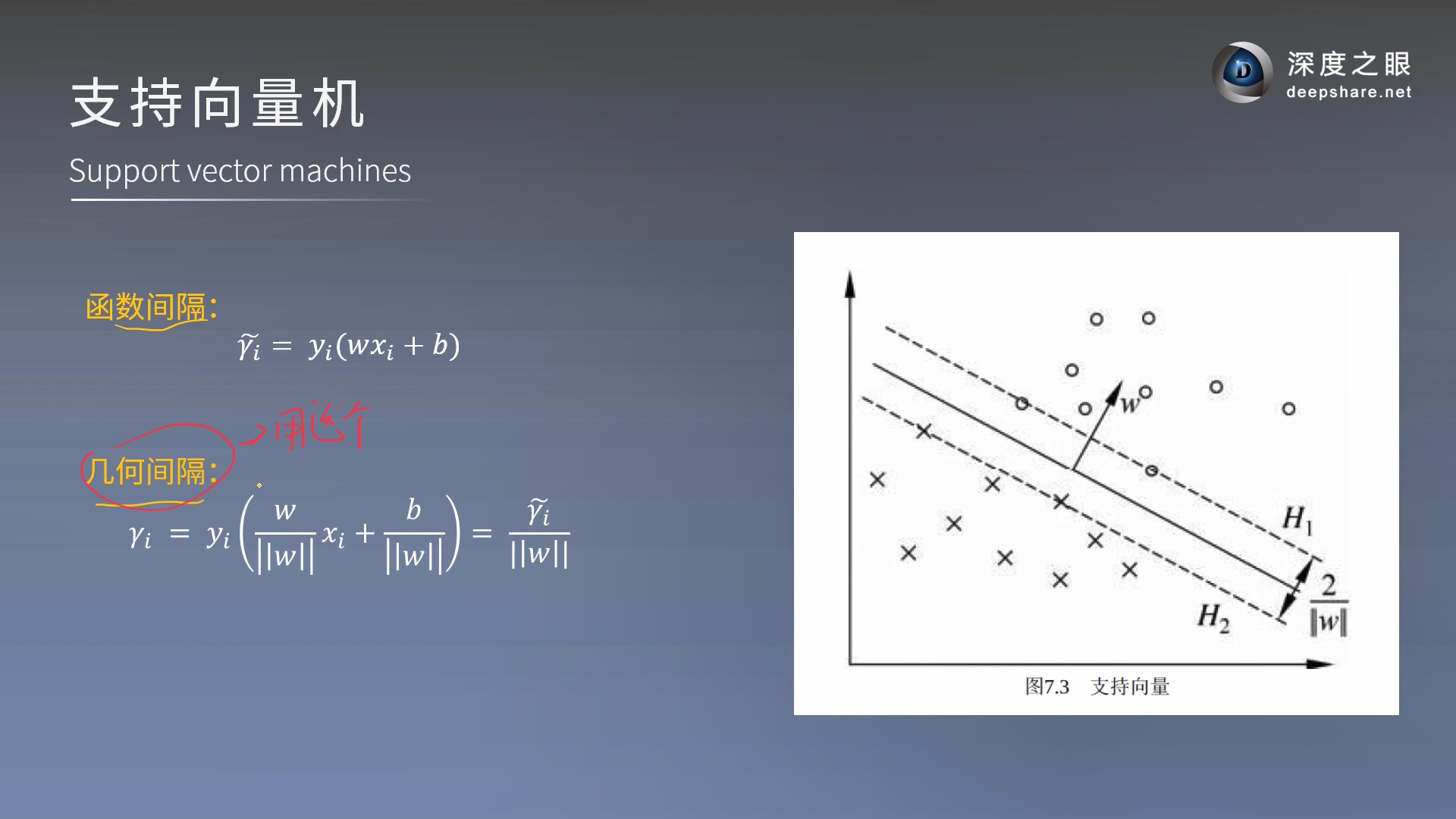
pure线性分类器

γ \gamma γ指的是几何间隔,是不会变的间隔, γ ′ \gamma^{'} γ′是函数间隔,是可变的间隔,所以我们通过变换将要求的几何间隔变为求函数间隔 γ ′ \gamma^{'} γ′,然后函数间隔可以等比例放大缩小,所以可以将其等比例放大缩小为1
对于 γ ′ \gamma^{'} γ′和 γ \gamma γ指的是间隔最大化的距离(也就是说某一个点)

此时此刻我们将函数间隔等比例放大缩小为了1,所以是求max 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1,条件就是 s . t y i ( w T x i + b ) ≥ 1 ( i = 1 , 2 , . . . m ) \;\; s.t \;\; y_i(w^Tx_i + b) \geq 1 (i =1,2,...m) s.tyi(wTxi+b)≥1(i=1,2,...m),要求那个最大值,我们可以等价转换求 m i n 1 2 ∣ ∣ w ∣ ∣ 2 2 min \;\; \frac{1}{2}||w||_2^2 min21∣∣w∣∣22(高数拉格朗日的原理不能忘记)
下面列拉格朗日乘子法列的式子
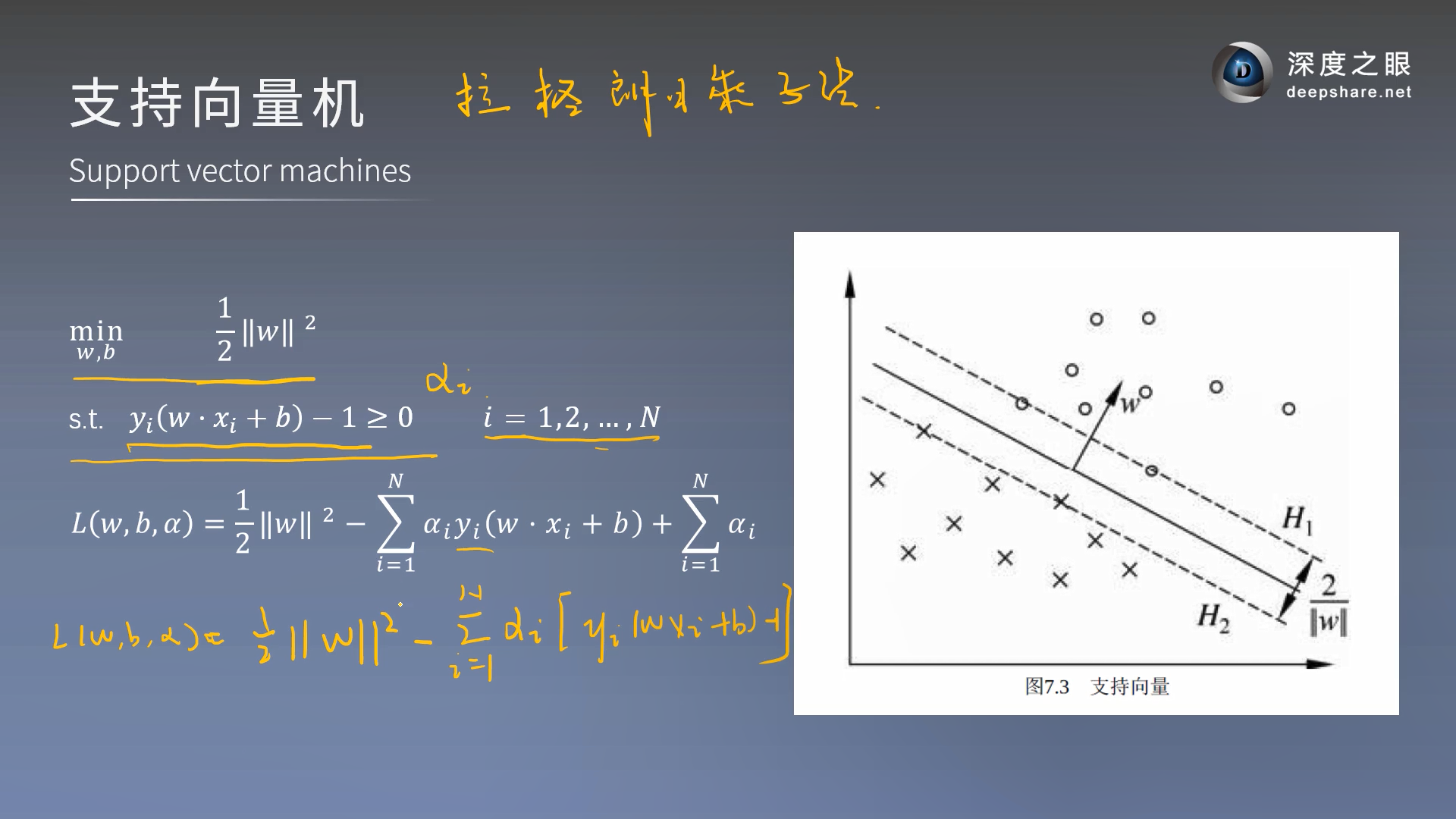
α i \alpha_i αi就是拉格朗日乘子法里面设的未知数
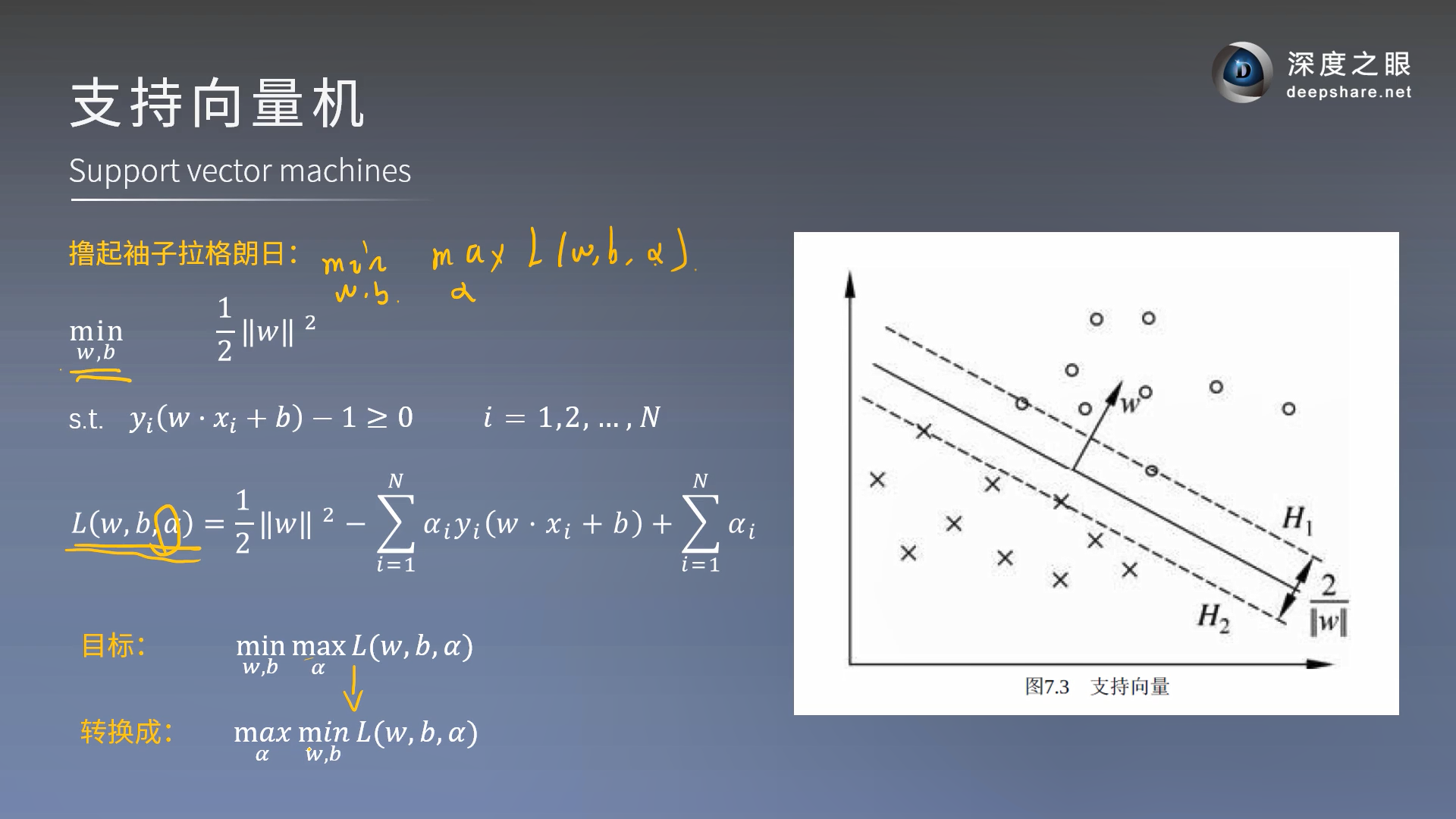
转换为求这个的对偶问题(后面的有些操作和最大熵式子的推导及其类似)]

分别对w和b求导得到上面两个式子,将这两个式子带入 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)
化简过程如下

dodo老师的化简过程

m a x ⏟ α i ≥ 0 m i n ⏟ w , b L ( w , b , α ) \underbrace{max}_{\alpha_i \geq 0} \;\underbrace{min}_{w,b}\; L(w,b,\alpha) αi≥0 maxw,b minL(w,b,α)
求完了第一层的min接下来求第二层的max,求这个最大值


第二层的max的求法暂且不表,后面有方法来求
软间隔线性分类器

给入松弛变量,允许小部分进入边界(小部分误差)

当然,松弛变量不能白加,这是有成本的,每一个松弛变量 ξ i \xi_i ξi, 对应了一个代价 ξ i \xi_i ξi,这个就得到了我们的软间隔最大化的SVM学习条件如下:
m i n 1 2 ∣ ∣ w ∣ ∣ 2 2 + C ∑ i = 1 m ξ i min\;\; \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i min21∣∣w∣∣22+Ci=1∑mξi
s . t . y i ( w T x i + b ) ≥ 1 − ξ i ( i = 1 , 2 , . . . m ) s.t. \;\; y_i(w^Tx_i + b) \geq 1 - \xi_i \;\;(i =1,2,...m) s.t.yi(wTxi+b)≥1−ξi(i=1,2,...m)
ξ i ≥ 0 ( i = 1 , 2 , . . . m ) \xi_i \geq 0 \;\;(i =1,2,...m) ξi≥0(i=1,2,...m)
这里,C>0为惩罚参数,可以理解为我们一般回归和分类问题正则化时候的参数。C越大,对误分类的惩罚越大,C越小,对误分类的惩罚越小。
也就是说,我们希望 1 2 ∣ ∣ w ∣ ∣ 2 2 \frac{1}{2}||w||_2^2 21∣∣w∣∣22尽量小,误分类的点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中,需要调参来选择。
我们要求这个几何间隔的最大值和前面pure线性分类器类似
L ( w , b , ξ , α , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 2 + C ∑ i = 1 m ξ i − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] − ∑ i = 1 m μ i ξ i L(w,b,\xi,\alpha,\mu) = \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}\mu_i\xi_i L(w,b,ξ,α,μ)=21∣∣w∣∣22+Ci=1∑mξi−i=1∑mαi[yi(wTxi+b)−1+ξi]−i=1∑mμiξi
其中 μ i ≥ 0 , α i ≥ 0 \mu_i \geq 0, \alpha_i \geq 0 μi≥0,αi≥0,均为拉格朗日系数。
也就是说,我们现在要优化的目标函数是:
m i n ⏟ w , b , ξ m a x ⏟ α i ≥ 0 , μ i ≥ 0 , L ( w , b , α , ξ , μ ) \underbrace{min}_{w,b,\xi}\; \underbrace{max}_{\alpha_i \geq 0, \mu_i \geq 0,} L(w,b,\alpha, \xi,\mu) w,b,ξ minαi≥0,μi≥0, maxL(w,b,α,ξ,μ)
这个优化目标也满足KKT条件,也就是说,我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解如下:
m a x ⏟ α i ≥ 0 , μ i ≥ 0 , m i n ⏟ w , b , ξ L ( w , b , α , ξ , μ ) \underbrace{max}_{\alpha_i \geq 0, \mu_i \geq 0,} \; \underbrace{min}_{w,b,\xi}\; L(w,b,\alpha, \xi,\mu) αi≥0,μi≥0, maxw,b,ξ minL(w,b,α,ξ,μ)
我们可以先求优化函数对于w,b的极小值, 接着再求拉格朗日乘子α和 μ的极大值。
首先我们来求优化函数对于w,b,ξ的极小值,这个可以通过求偏导数求得:
∂ L ∂ w = 0 ⇒ w = ∑ i = 1 m α i y i x i \frac{\partial L}{\partial w} = 0 \;\Rightarrow w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i ∂w∂L=0⇒w=i=1∑mαiyixi
∂ L ∂ b = 0 ⇒ ∑ i = 1 m α i y i = 0 \frac{\partial L}{\partial b} = 0 \;\Rightarrow \sum\limits_{i=1}^{m}\alpha_iy_i = 0 ∂b∂L=0⇒i=1∑mαiyi=0
∂ L ∂ ξ = 0 ⇒ C − α i − μ i = 0 \frac{\partial L}{\partial \xi} = 0 \;\Rightarrow C- \alpha_i - \mu_i = 0 ∂ξ∂L=0⇒C−αi−μi=0
然后利用这个式子消除w和b
L ( w , b , ξ , α , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 2 + C ∑ i = 1 m ξ i − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] − ∑ i = 1 m μ i ξ i = 1 2 ∣ ∣ w ∣ ∣ 2 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] + ∑ i = 1 m α i ξ i = 1 2 ∣ ∣ w ∣ ∣ 2 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 ] = 1 2 w T w − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = 1 2 w T ∑ i = 1 m α i y i x i − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = 1 2 w T ∑ i = 1 m α i y i x i − w T ∑ i = 1 m α i y i x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = − 1 2 w T ∑ i = 1 m α i y i x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = − 1 2 w T ∑ i = 1 m α i y i x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ( ∑ i = 1 m α i y i x i ) T ( ∑ i = 1 m α i y i x i ) − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 m α i y i x i T ∑ i = 1 m α i y i x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 m α i y i x i T ∑ i = 1 m α i y i x i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 , j = 1 m α i y i x i T α j y j x j + ∑ i = 1 m α i = ∑ i = 1 m α i − 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j \begin{align} L(w,b,\xi,\alpha,\mu) & = \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}\mu_i\xi_i \\&= \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] + \sum\limits_{i=1}^{m}\alpha_i\xi_i \\& = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \\& = \frac{1}{2}w^Tw-\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i -\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}(\sum\limits_{i=1}^{m}\alpha_iy_ix_i)^T(\sum\limits_{i=1}^{m}\alpha_iy_ix_i) - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_iy_ix_i^T\alpha_jy_jx_j + \sum\limits_{i=1}^{m}\alpha_i \\& = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \end{align} L(w,b,ξ,α,μ)=21∣∣w∣∣22+Ci=1∑mξi−i=1∑mαi[yi(wTxi+b)−1+ξi]−i=1∑mμiξi =21∣∣w∣∣22−i=1∑mαi[yi(wTxi+b)−1+ξi]+i=1∑mαiξi=21∣∣w∣∣22−i=1∑mαi[yi(wTxi+b)−1]=21wTw−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=21wTi=1∑mαiyixi−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=21wTi=1∑mαiyixi−wTi=1∑mαiyixi−i=1∑mαiyib+i=1∑mαi=−21wTi=1∑mαiyixi−i=1∑mαiyib+i=1∑mαi=−21wTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=−21(i=1∑mαiyixi)T(i=1∑mαiyixi)−bi=1∑mαiyi+i=1∑mαi=−21i=1∑mαiyixiTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=−21i=1∑mαiyixiTi=1∑mαiyixi+i=1∑mαi=−21i=1,j=1∑mαiyixiTαjyjxj+i=1∑mαi=i=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
这个结果和pure线性分类器结果一样,唯一不一样的是约束条件
m a x ⏟ α ∑ i = 1 m α i − 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j \underbrace{ max }_{\alpha} \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j α maxi=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
s . t . ∑ i = 1 m α i y i = 0 s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 s.t.i=1∑mαiyi=0
C − α i − μ i = 0 C- \alpha_i - \mu_i = 0 C−αi−μi=0
α i ≥ 0 ( i = 1 , 2 , . . . , m ) \alpha_i \geq 0 \;(i =1,2,...,m) αi≥0(i=1,2,...,m)
μ i ≥ 0 ( i = 1 , 2 , . . . , m ) \mu_i \geq 0 \;(i =1,2,...,m) μi≥0(i=1,2,...,m)
对于 C − α i − μ i = 0 , α i ≥ 0 , μ i ≥ 0 C- \alpha_i - \mu_i = 0 , \alpha_i \geq 0 ,\mu_i \geq 0 C−αi−μi=0,αi≥0,μi≥0这3个式子,我们可以得到 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C
m i n ⏟ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j − ∑ i = 1 m α i \underbrace{ min }_{\alpha} \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j - \sum\limits_{i=1}^{m}\alpha_i α min21i=1,j=1∑mαiαjyiyjxiTxj−i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 s.t.i=1∑mαiyi=0\
0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C和pure线性分类器比就多了这个约束条件,求 α \alpha α和pure那个一样通过SMO算法来求上式极小化时对应的α向量就可以求出w和b了。

引入核函数

这里x是向量,怎么方便求向量的点积,需要引入核函数


幂函数好使

SMO


我们假设我们通过SMO算法求得了我们得到了对应的α的值 α ∗ \alpha^{*} α∗。
那么我们根据 w = ∑ i = 1 m α i y i x i w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i w=i=1∑mαiyixi,可以求出对应的w的值 w ∗ = ∑ i = 1 m α i ∗ y i x i w^{*} = \sum\limits_{i=1}^{m}\alpha_i^{*}y_ix_i w∗=i=1∑mαi∗yixi
求b则稍微麻烦一点。注意到,对于任意支持向量 ( x x , y s ) (x_x, y_s) (xx,ys),都有
y s ( w T x s + b ) = y s ( ∑ i = 1 m α i y i x i T x s + b ) = 1 y_s(w^Tx_s+b) = y_s(\sum\limits_{i=1}^{m}\alpha_iy_ix_i^Tx_s+b) = 1 ys(wTxs+b)=ys(i=1∑mαiyixiTxs+b)=1(到超平面的函数距离人为设置为1)
假设我们有S个支持向量,则对应我们求出S个 b ∗ b^{*} b∗,理论上这些 b ∗ b^{*} b∗都可以作为最终的结果, 但是我们一般采用一种更健壮的办法,即求出所有支持向量所对应的 b s ∗ b_s^{*} bs∗,然后将其平均值作为最后的结果。注意到对于严格线性可分的SVM,b的值是有唯一解的(那是肯定的,因为对于二维而言,支持向量到最优超平面之间的距离是一样的都是1),也就是这里求出的所有 b ∗ b^{*} b∗都是一样的,这里我们仍然这么写是为了和后面加入软间隔后的SVM的算法描述一致。
支持向量:和超平面平行的保持一定的函数距离的这两个超平面对应的向量(不是法向量),相当于A,B两点画平行线(支持向量),然后平行线之间的距离最大就是最优的超平面

(我们已经得到最优超平面的前提下,需要求支持向量)怎么得到支持向量呢?根据KKT条件中的对偶互补条件 α i ∗ ( y i ( w T x i + b ) − 1 ) = 0 \alpha_{i}^{*}(y_i(w^Tx_i + b) - 1) = 0 αi∗(yi(wTxi+b)−1)=0,如果 α i > 0 \alpha_i>0 αi>0则有 y i ( w T x i + b ) = 1 y_i(w^Tx_i + b) =1 yi(wTxi+b)=1即点在支持向量上,否则如果 α i = 0 \alpha_i=0 αi=0(无约束条件问题),则有 y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i + b) \geq 1 yi(wTxi+b)≥1,即样本在支持向量上或者已经被正确分类。
相关文章:

SVM支持向量机
SVM的由来和概念 间隔最大化是找最近的那个点的距离’ 之前我们学习的都是线性超平面,现在我们要将超平面变成圈 对于非线性问题升维来解决 对于下图很难处理,我们可以将棍子立起来,然后说不定red跑到左边了,green跑到右边了(可能增加了某种筛选条件导致两个豆子分离)(只是一种…...
【Unity】RPG2D龙城纷争(二)关卡、地块
更新日期:2024年6月12日。 项目源码:后续章节发布 索引 简介地块(Block)一、定义地块类二、地块类型三、地块渲染四、地块索引 关卡(Level)一、定义关卡类二、关卡基础属性三、地块集合四、关卡初始化五、关…...
mediamtx流媒体服务器测试
MediaMTX简介 在web页面中直接播放rtsp视频流,重点推荐:mediamtx,不仅仅是rtsp-CSDN博客 mediamtx github MediaMTX(以前的rtsp-simple-server)是一个现成的和零依赖的实时媒体服务器和媒体代理,允许发布,读取&…...

C# 循环
C# 循环 在编程中,循环是一种控制结构,它允许我们重复执行一段代码多次。C# 提供了几种循环机制,以适应不同的编程需求。本文将详细介绍 C# 中常用的几种循环类型,包括 for 循环、while 循环、do-while 循环和 foreach 循环&…...

PHP杂货铺家庭在线记账理财管理系统源码
家庭在线记帐理财系统,让你对自己的开支了如指掌,图形化界面操作更简单,非常适合家庭理财、记账,系统界面简洁优美,操作直观简单,非常容易上手。 安装说明: 1、上传到网站根目录 2、用phpMyad…...
)
机器学习中的神经网络重难点!纯干货(上篇)
. . . . . . . . .纯干货 . . . . . . 目录 前馈神经网络 基本原理 公式解释 一个示例 卷积神经网络 基本原理 公式解释 一个示例 循环神经网络 基本原理 公式解释 一个案例 长短时记忆网络 基本原理 公式解释 一个示例 自注意力模型 基本原理…...

[DDR4] DDR1 ~ DDR4 发展史导论
依公知及经验整理,原创保护,禁止转载。 专栏 《深入理解DDR4》 内存和硬盘是电脑的左膀右臂, 挑起存储的大梁。因为内存的存取速度超凡地快, 但内存上的数据掉电又会丢失,一直其中缓存的作用,就像是我们的工…...
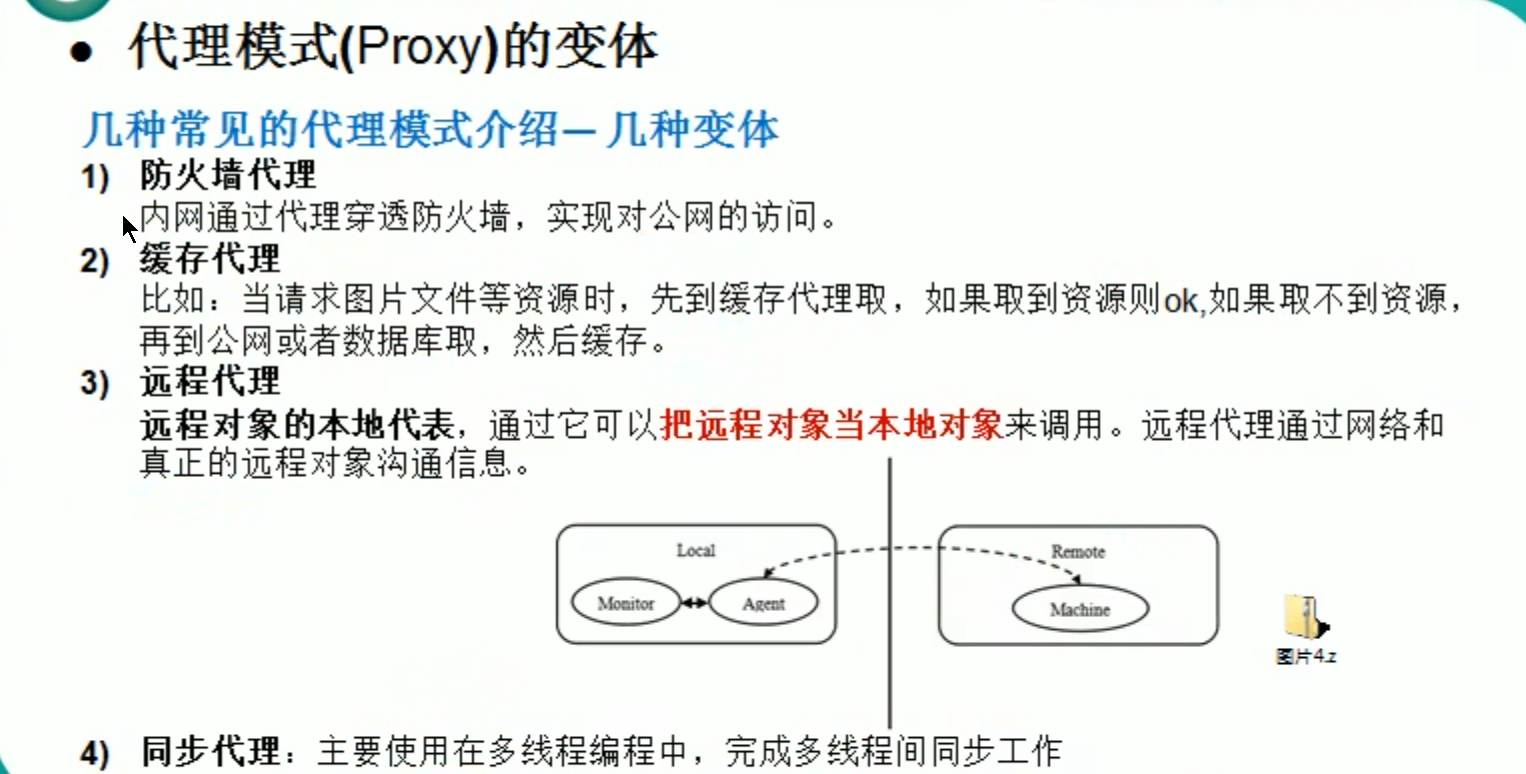
享元和代理模式
文章目录 享元模式1.引出享元模式1.展示网站项目需求2.传统方案解决3.问题分析 2.享元模式1.基本介绍2.原理类图3.外部状态和内部状态4.类图5.代码实现1.AbsWebSite.java 抽象的网站2.ConcreteWebSite.java 具体的网站,type属性是内部状态3.WebSiteFactory.java 网站…...

[英语单词] ellipsize,动词化后缀 -ize
openvswitch manual里的一句话:里面有使用ellipsize,但是查字典是没有这个单词,这就是创造出来的动词。将单词ellipsis,加动词化后缀,-ize。 Often we ellipsize arguments not important to the discussion, e.g.: &…...

自然资源-测绘地信专业术语,值得收藏!
自然资源-测绘地信专业术语,值得收藏! 1、1954年北京坐标系 1954年我国决定采用的国家大地坐标系,实质上是由原苏联普尔科沃为原点的1942年坐标系的延伸。 2、1956年黄海高程系统 根据青岛验潮站1950年一1956年的验潮资料计算确定的平均海面…...

如何在小程序中实现页面之间的返回
在小程序中实现页面之间的返回,通常有以下几种方法,这些方法各有特点,适用于不同的场景: 1. 使用wx.navigateBack方法 描述:wx.navigateBack是微信小程序中用于关闭当前页面,返回上一页面或多级页面的API…...

深入解析数据结构之B树:平衡树中的王者
在计算机科学中,数据结构是算法和程序设计的基础。而在众多数据结构中,B树作为一种平衡树,在数据库和文件系统中有着广泛应用。本文将详细介绍B树的概念、特点、操作、优缺点及其应用场景,帮助读者深入理解这一重要的数据结构。 …...
18. 第十八章 继承
18. 继承 和面向对象编程最常相关的语言特性就是继承(inheritance). 继承值得是根据一个现有的类型, 定义一个修改版本的新类的能力. 本章中我会使用几个类来表达扑克牌, 牌组以及扑克牌性, 用于展示继承特性.如果你不玩扑克, 可以在http://wikipedia.org/wiki/Poker里阅读相关…...
)
OperationalError: (_mysql_exceptions.OperationalError)
OperationalError: (_mysql_exceptions.OperationalError) (2006, MySQL server has gone away) 这个错误通常表示客户端(例如你的 Python 程序使用 SQLAlchemy 连接到 MySQL 数据库)和 MySQL 服务器之间的连接被异常关闭了。这个问题可能由多种原因引起,以下是一些常见的原…...

DocGraph相关概念
结合简化版的直观性和专业版的深度,我们可以得到一个既易于理解又包含专业细节的DocGraph概念讲解。 DocGraph概述(简化版) 想象DocGraph就像是文章信息的地图。它通过拆分文档、识别关键词、分析关系,并最终以图形方式呈现这些…...
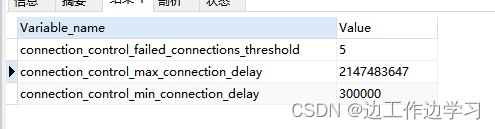
MySQL限制登陆失败次数配置
目录 一、限制登陆策略 1、Windows 2、Linux 一、限制登陆策略 1、Windows 1)安装插件 登录MySQL数据库 mysql -u root -p 执行命令安装插件 #限制登陆失败次数插件 install plugin CONNECTION_CONTROL soname connection_control.dll;install plugin CO…...

洛谷题解 - P1192 台阶问题
目录 题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示代码 题目描述 有 N N N 级台阶,你一开始在底部,每次可以向上迈 1 ∼ K 1\sim K 1∼K 级台阶,问到达第 N N N 级台阶有多少种不同方式。 输入格式 两个正整数 N , K …...
Unity贪吃蛇改编【详细版】
Big and small greedy snakes 游戏概述 游戏亮点 通过对称的美感,设置两条贪吃蛇吧,其中一条加倍成长以及加倍减少,另一条正常成长以及减少,最终实现两条蛇对整个界面的霸占效果。 过程中不断记录两条蛇的得分情况,…...

React中数据响应式原理
React作为当下最流行的前端框架之一,以其声明式编程和组件化架构而广受开发者喜爱。而React的数据响应式原理,是其高效更新DOM的核心机制。本文将深入探讨React中数据响应式原理,并结合代码示例进行论证。 响应式原理概述 在React中&#x…...
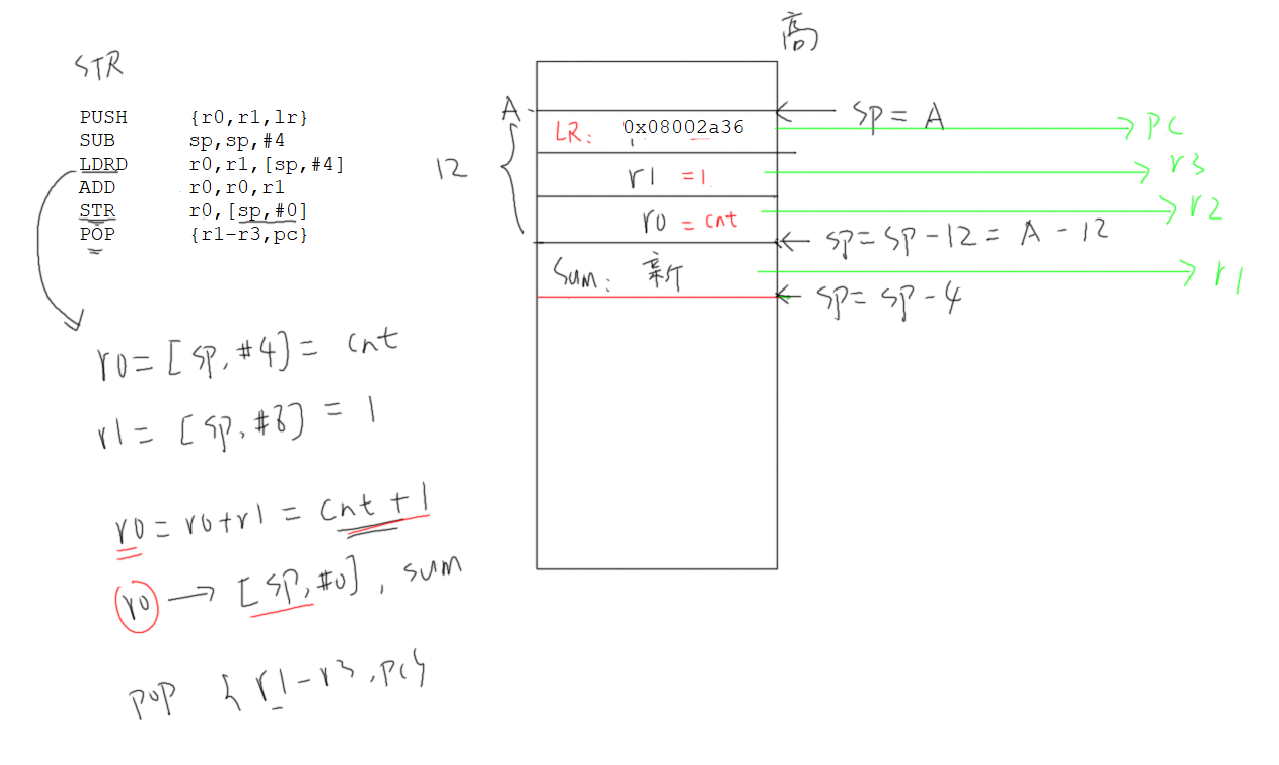
【FreeRTOS】ARM架构汇编实例
目录 ARM架构简明教程1. ARM架构电脑的组成1.2 RISC1.2 提出问题1.3 CPU内部寄存器1.4 汇编指令 2. C函数的反汇编 学习视频 【FreeRTOS入门与工程实践 --由浅入深带你学习FreeRTOS(FreeRTOS教程 基于STM32,以实际项目为导向)】 https://www.…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
