Arnoldi Iteration 思考
文章目录
- 1. 投影平面
- 2. Arnoldi Iteration
- 3. python 代码
1. 投影平面
假设我们有一个向量q,我们需要关于向量q,构建一个投影平面P,使得给定任何向量v,可以通过公式 p = P v p=Pv p=Pv,快速得到向量v在投影平面P上的投影向量p.
- 计算向量内积,向量v在向量q上的投影长度|p|
v T q = ∣ v ∣ ∣ q ∣ cos θ = ∣ p ∣ ∣ q ∣ → ∣ p ∣ = v T q ∣ q ∣ \begin{equation} v^Tq=|v||q|\cos{\theta}=|p||q|\rightarrow |p|=\frac{v^Tq}{|q|} \end{equation} vTq=∣v∣∣q∣cosθ=∣p∣∣q∣→∣p∣=∣q∣vTq - 我们知道,q方向上的单位向量为 q ∣ q ∣ \frac{q}{|q|} ∣q∣q,那么投影向量p可得, v T q v^Tq vTq为标量,
随便放位置
p = ∣ p ∣ ⋅ q ∣ q ∣ = v T q ∣ q ∣ ⋅ q ∣ q ∣ = v T q q T q q \begin{equation} p=|p|\cdot \frac{q}{|q|} =\frac{v^Tq}{|q|}\cdot \frac{q}{|q|}=\frac{v^Tq}{q^Tq}q \end{equation} p=∣p∣⋅∣q∣q=∣q∣vTq⋅∣q∣q=qTqvTqq - 重点!内积可以随便转换,并且标量位置可以随便放!
v T q = q T v \begin{equation} v^Tq=q^Tv \end{equation} vTq=qTv - 整理可得:
p = q T v q T q q = q T v q q T q \begin{equation} p=\frac{q^Tv}{q^Tq}q=\frac{q^Tvq}{q^Tq} \end{equation} p=qTqqTvq=qTqqTvq - 标量位置随意可得: q T v q → q q T v q^Tvq\rightarrow qq^Tv qTvq→qqTv
p = q T v q q T q = q q T q T q v \begin{equation} p=\frac{q^Tvq}{q^Tq}= \frac{qq^T}{q^Tq}v \end{equation} p=qTqqTvq=qTqqqTv - 第一个是投影矩阵P
P = q q T q T q , p = P v \begin{equation} P=\frac{qq^T}{q^Tq},p=Pv \end{equation} P=qTqqqT,p=Pv - 第二,快速计算一个向量v在向量q上的投影p
p = q T v q q T q \begin{equation} p=\frac{q^Tvq}{q^Tq} \end{equation} p=qTqqTvq - 第三,当q为单位向量的时候, q T q = ∣ q ∣ 2 = 1 q^Tq=|q|^2=1 qTq=∣q∣2=1,像不像二次型形式,就是这么神奇!
p = q T v q \begin{equation} p=q^Tvq \end{equation} p=qTvq - 第四 ,一般情况下计算垂直向量e,向量几何关系可得v=p+e,
e = v − p = v − q T v q q T q \begin{equation} e=v-p=v-\frac{q^Tvq}{q^Tq} \end{equation} e=v−p=v−qTqqTvq
第五,特殊情况下,|q|=1,整理可得:
e = v − q T v q \begin{equation} e=v-q^Tvq \end{equation} e=v−qTvq

2. Arnoldi Iteration
arnoldi Iteration的作用是想在原来的krylov 子空间中增加一个向量 A q k Aq_k Aqk,具体思路如下图所示:


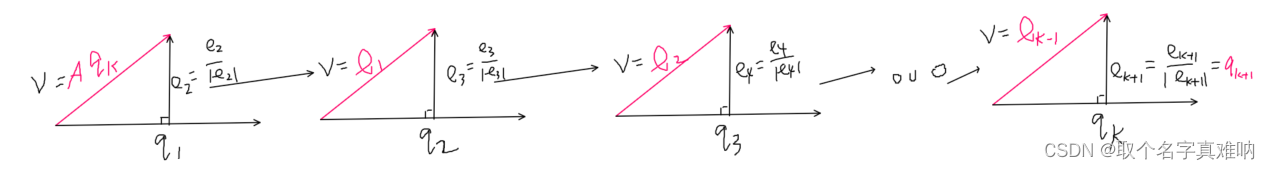
- 小结:arnoldi Iteration 本质上就是新建一个向量 v v v,为了让v向量和以前已知的向量 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk垂直,通过不断迭代,将v向量减去掉所有在 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk上的投影向量 e k e_k ek,这样最后得到的向量 q k q_k qk就一定是垂直于 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk
3. python 代码
后续提供详细的,现在直接粘贴吧。
import numpy as npdef arnoldi_iteration(A, b, k):"""Perform Arnoldi iteration to generate an orthonormal basis for the Krylov subspace.Parameters:A : numpy.ndarrayThe input matrix (n x n).b : numpy.ndarrayThe initial vector (n, ).k : intThe number of iterations, which defines the size of the Krylov subspace.Returns:Q : numpy.ndarrayThe orthonormal basis for the Krylov subspace (n x (k+1)).H : numpy.ndarrayThe Hessenberg matrix (k+1 x k)."""n = A.shape[0]Q = np.zeros((n, k + 1)) # Orthonormal basisH = np.zeros((k + 1, k)) # Hessenberg matrix# Normalize the initial vectorQ[:, 0] = b / np.linalg.norm(b)for j in range(k):v = A @ Q[:, j] # Matrix-vector multiplicationfor i in range(j + 1):H[i, j] = np.dot(Q[:, i].conj(), v) # Project v onto the current basis vectorsv = v - H[i, j] * Q[:, i] # Make v orthogonal to Q[:, i]H[j + 1, j] = np.linalg.norm(v) # Normalize v to get the next basis vectorif H[j + 1, j] != 0 and j + 1 < k:Q[:, j + 1] = v / H[j + 1, j]return Q, H# Example usage
if __name__ == "__main__":# Define a random matrix A and a random vector bA = np.random.rand(5, 5)b = np.random.rand(5)k = 4Q, H = arnoldi_iteration(A, b, k)print("Orthonormal basis Q:\n", Q)print("Hessenberg matrix H:\n", H)相关文章:
Arnoldi Iteration 思考
文章目录 1. 投影平面2. Arnoldi Iteration3. python 代码 1. 投影平面 假设我们有一个向量q,我们需要关于向量q,构建一个投影平面P,使得给定任何向量v,可以通过公式 p P v pPv pPv,快速得到向量v在投影平面P上的投影向量p. 计算向量内积,…...

【Kafka】SpringBoot整合Kafka详细介绍及代码示例
Kafka介绍 Apache Kafka是一个分布式流处理平台。它最初由LinkedIn开发,后来成为Apache软件基金会的一部分,并在开源社区中得到了广泛应用。Kafka的核心概念包括Producer、Consumer、Broker、Topic、Partition和Offset。 Producer:生产者&a…...

C++ 质数因子分解
描述 功能:输入一个正整数,按照从小到大的顺序输出它的所有质因子(重复的也要列举)(如180的质因子为2 2 3 3 5 ) 输入描述: 输入一个整数 输出描述: 按照从小到大的顺序输出它的所有质数的…...
laravel版本≥ 8.1
laravel10 php ≥ 8.1 且 ≤ 8.3? 8.1 < php < 8.3PHP版本要求在 8.1 到 8.3 之间,包括这两个版本。具体来说:"≥ 8.1" 表示 PHP 的版本至少是 8.1,也就是说 8.1 及以上的版本都可以。 "≤ 8.3" 表示 P…...
【iOS】MRC下的单例模式批量创建单例
单例模式的介绍和ARC下的单例请见这篇:【iOS】单例模式 目录 关闭ARC环境MRC下的单例ARC下的单例批量创建单例Demo 关闭ARC环境 首先关闭ARC环境,即打开MRC: 或是指定某特定目标文件为非ARC环境: 双击某个类文件,指定…...

计算机网络期末复习
今天考专四,环境都蛮好的,试卷也很新,老师人也不错,明年再来。 又到期末考试咯,大家复习没有?还没复习啊?还不复???? 目录 第一章 1-02 试简述…...

python写一个获取竞品信息报告
要编写一个获取竞品信息报告的Python程序,首先需要明确您想要获取的竞品信息以及数据来源。在这个示例中,我将展示如何从网页提取竞品信息,并编写一个简单的报告。 假设您想要获取以下竞品信息: 1. 产品名称 2. 产品价格 3. 产品特…...

一文彻底理解机器学习 ROC-AUC 指标
在机器学习和数据科学的江湖中,评估模型的好坏是非常关键的一环。而 ROC(Receiver Operating Characteristic)曲线和 AUC(Area Under Curve)正是评估分类模型性能的重要工具。 这个知识点在面试中也很频繁的出现。尽管…...

【二】【动态规划NEW】91. 解码方法,62. 不同路径,63. 不同路径 II
91. 解码方法 一条包含字母 A-Z 的消息通过以下映射进行了 编码 : ‘A’ -> “1” ‘B’ -> “2” … ‘Z’ -> “26” 要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法ÿ…...

Python闯LeetCode--第3题:无重复字符的最长子串
Problem: 3. 无重复字符的最长子串 文章目录 思路解题方法复杂度Code 思路 一上来马上想到两层for循环暴力枚举,但是又立马想到复杂度是 O ( n 2 ) O(n^2) O(n2),思考了一下能否有更优解,于是想到用头尾两个指针来指定滑动窗口(主…...

HTML DOM 对象
HTML DOM 对象 1. 概述 HTML DOM(文档对象模型)是一个跨平台和语言独立的接口,它允许程序和脚本动态地访问和更新文档的内容、结构和样式。在HTML DOM中,文档被表示为节点树,其中每个节点代表文档中的一个部分,例如元素、文本或属性。HTML DOM对象是构成这个节点树的基…...

如何解决 BeautifulSoup 安装问题:从 BeautifulSoup 3 到 BeautifulSoup 4
在使用 Python 的过程中,解析 HTML 和 XML 数据是一项常见任务。BeautifulSoup 是一个非常流行的解析库。然而,最近在安装 BeautifulSoup 时,遇到了一些问题。本文将介绍如何解决这些问题,并成功安装 BeautifulSoup 4。 问题描述 …...

原型模式--深复制/浅复制
原型模式用于克隆复杂对象,由于new一个实例对象会消耗大部分时间,所以原型模式可以节约大量时间 1 public class Sheep implements Cloneable{2 private String name;3 private Date birth;4 public Sheep(String name, Date birth) {5 …...
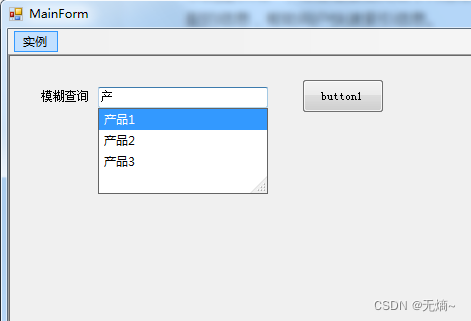
C# TextBox模糊查询及输入提示
在程序中,我们经常会遇到文本框中不知道输入什么内容,这时我们可以在文本框中显示提示词提示用户;或者需要查询某个内容却记不清完整信息,通常可以通过文本框列出与输入词相匹配的信息,帮助用户快速索引信息。 文本框…...
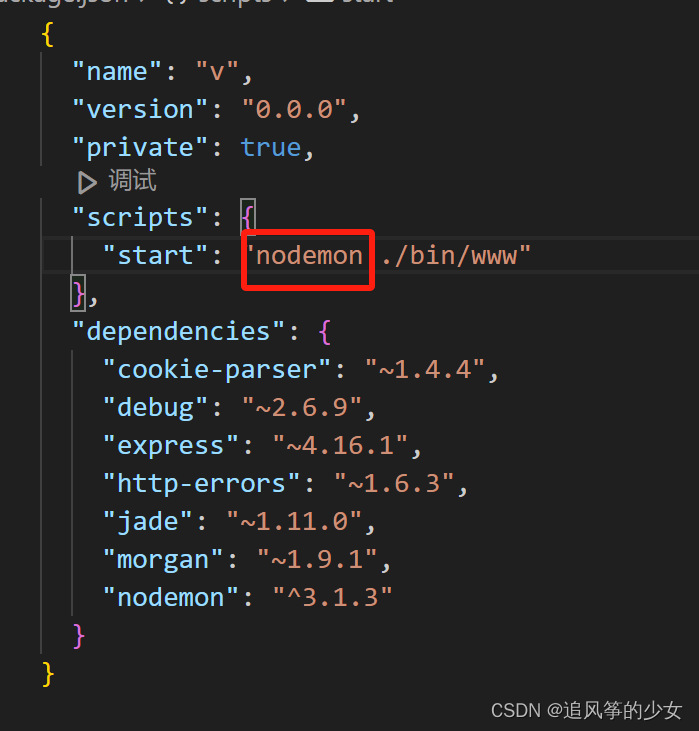
Node入门以及express创建项目
前言 记录学习NodeJS 一、NodeJS是什么? Node.js 是一个开源和跨平台的 JavaScript 运行时环境 二、下载NodeJs 1.下载地址(一直点击next即可,记得修改安装地址) https://nodejs.p2hp.com/download/ 2.查看是否安装成功,打开命令行 nod…...
Cheat Engine CE v7.5 安装教程(专注于游戏的修改器)
前言 Cheat Engine是一款专注于游戏的修改器。它可以用来扫描游戏中的内存,并允许修改它们。它还附带了调试器、反汇编器、汇编器、变速器、作弊器生成、Direct3D操作工具、系统检查工具等。 一、下载地址 下载链接:http://dygod/source 点击搜索&…...
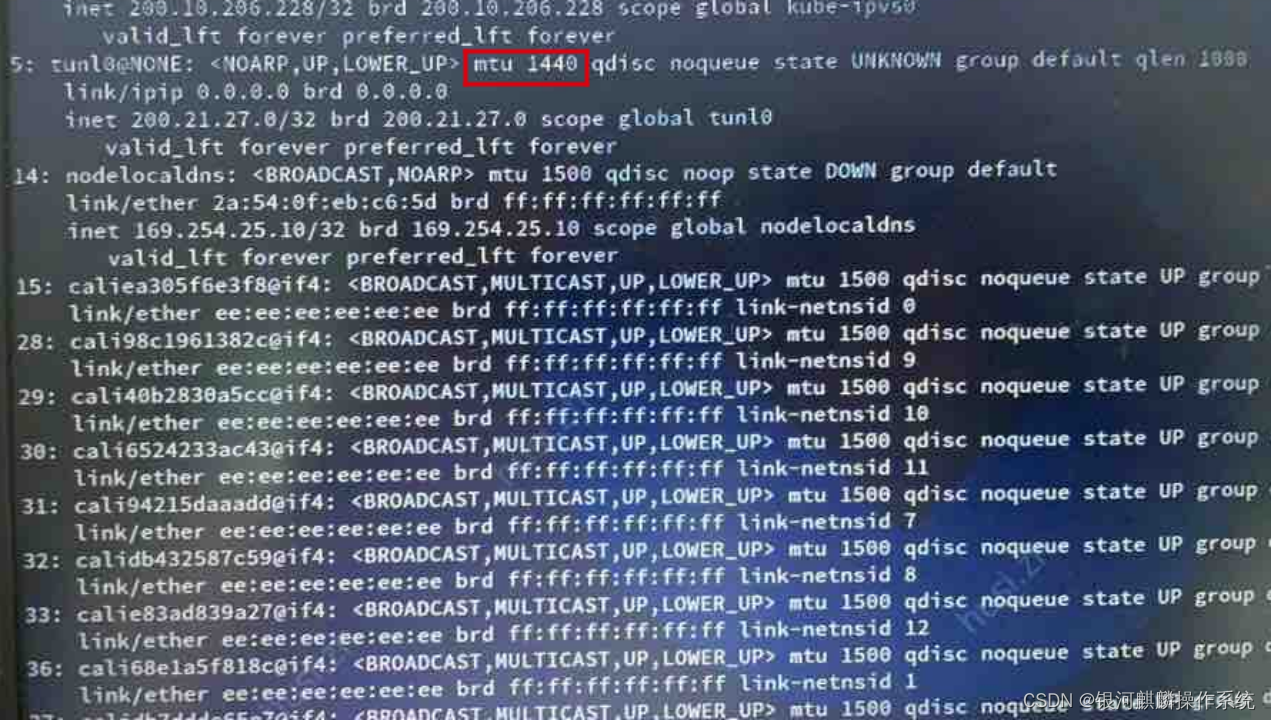
【实例分享】访问后端服务超时,银河麒麟服务器操作系统分析及处理建议
1.服务器环境以及配置 【机型】 处理器: Intel 32核 内存: 128G 整机类型/架构: x86_64虚拟机 【内核版本】 4.19.90-25.22.v2101.kylin.x86_64 【OS镜像版本】 kylin server V10 SP2 【第三方软件】 开阳k8s 2.问题现象描述 …...

Java中和的区别
在Java中,& 和 && 都是逻辑运算符,但它们之间存在一些重要的区别,特别是在它们如何评估其操作数以及它们的性能影响方面。 短路评估(Short-Circuit Evaluation): &&(逻辑…...
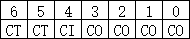
深入理解计算机系统 CSAPP 家庭作业6.34
第一步先求(S,E,B,m) 题目说共C32个字节,块大小B为16个字节,那就是分为两组:0,1.然后每组存4个int 每个4字节 CB*E*S .B16 ,直接映射的E就是1,所以S2 m为啥等于7? 通过写出两个数组所有的地址可以得出m7. 得出高速缓存的参数:(S,E,B,m)(2,1,16,7),注意图6-26每个参数的定义…...

[leetcode 141环形链表]双指针解决环形链表
Problem: 141. 环形链表 文章目录 思路Code 思路 首先想到如果链表为空直接返回false 其次想到用双指针,一个一回走一步,另一个一回走两步 如果是环形,总有一个时刻,两指针会指向同一个节点,而且该结点不能为空(空是快指针遍历完单链表了) Code /*** Definition for singly-li…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
