求一个补码表示数的原始值的三种方式
求一个补码表示数的原始值的三种方式
假设 a=(10010)2′complement=−14a = (10010)_{2'complement}=-14a=(10010)2′complement=−14
方式1,通过补码求原始值公式求值(see article)
x=−xM−1∗2M−1+∑i=0M−2xi∗2ix=-x_{M-1}*2^{M-1}+\sum_{i=0}^{M-2}x_i*2^ix=−xM−1∗2M−1+i=0∑M−2xi∗2i
其中,M表示位宽,例如,对于a来说,M=5。
所以,a=−1∗24+0∗23+0∗22+1∗21+0∗20=−14a=-1*2^4+0*2^3+0*2^2+1*2^1+0*2^0=-14a=−1∗24+0∗23+0∗22+1∗21+0∗20=−14
方式2,通过绝对值来求负数补码的原始值
前提是该数的符号位必须是1,也就是说它必须是复数
求一个负数(补码表示)的绝对值,只需将其连同符号位全部取反再加1,即得到该负数的绝对值,例如,对数a求绝对值,先整体取反得到01101,再加1,得到01110,即14。接着只需要为绝对值添加负号,就可以获得a的原始值了。
方式3,通过模的概念去求负数补码的绝对值(see article)
−(2′complementofx)=−(2M−x)-(2'complement of x) = -(2^M-x)−(2′complementofx)=−(2M−x)
相关文章:

求一个补码表示数的原始值的三种方式
求一个补码表示数的原始值的三种方式假设 a(10010)2′complement−14a (10010)_{2complement}-14a(10010)2′complement−14 方式1,通过补码求原始值公式求值(see article) x−xM−1∗2M−1∑i0M−2xi∗2ix-x_{M-1}*2^{M-1}\sum_{i0}^{M-2…...

【计算机组成原理】
第2章 运算方法和运算器 2.1 数据与文字的表示方法 2.1.1 数据格式 定点数的表示方法 定点纯小数纯小数表示范围定点纯整数定点表示法特点 浮点数的表示方法: 浮点的规格化表示:阶码、尾数、指数、基数IEEE754标准:单精度、双精度浮点数表…...

论文分享:图像识别与隐私安全
1、基于差分隐私框架的频域下人脸识别隐私保护算法Privacy-Preserving Face Recognition with Learnable Privacy Budget in Frequency Domain2、一种基于视觉密码学和可信计算的无密钥依赖的医学图像安全隐私保护框架A Privacy Protection Framework for Medical Image Securi…...

计算机基础小结
目录 ❤ 计算机基础编程 什么是编程语言? 什么是编程? 为什么要学习编程? ❤ 计算机组成原理 控制器 运算器 储存器 内存(主存) 外存 输入设备 输出设备 适配器 总线 机械硬盘 固态硬盘 ❤ 计算机操作系统 什么是操作系统? 什么是文件? 什么是应…...
Linux服务器还有漏洞?建议使用 OpenVAS 日常检查!
几乎每天都会有新的系统漏洞产生,系统管理员经常忙于管理服务器,有时候会忽略一些很明显的安全问题。扫描 Linux 服务器以查找安全问题并不是很简单的事情,所以有时候需要借助于一些专门的工具。 OpenVAS 就是这样一种开源工具,它…...
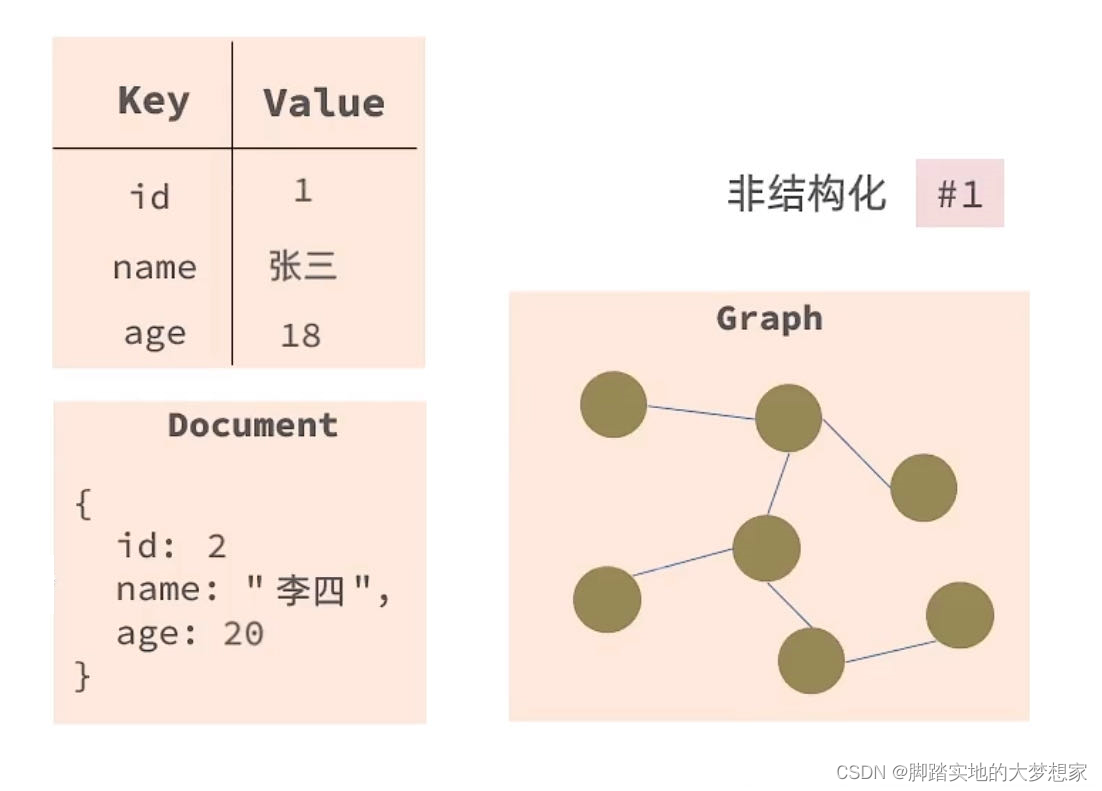
【Redis】P1 Redis - NoSQL
Redis - NoSQLSQL 与 NoSQL差别一:结构化 与 非结构化差别二:关联性 与 非关联性差别三:规范化查询语句 与 非规范化差别四:事务 与 无事务差别五:磁盘存储 与 内存存储RedisRedis 的安装当前数据库存储主要分为 关系型…...
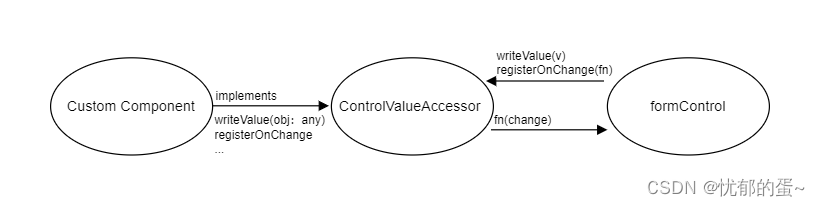
Angular学习之ControlValueAccessor接口详解
ControlValueAccessor 是什么?为什么需要使用 ?下面本篇文章就来带大家了解Angular中的ControlValueAccessor组件接口,希望对大家有所帮助! ControlValueAccessor 是什么? 简单来说ControlValueAccessor是一个接口&am…...

【GORM】高级查询方案
【GORM】高级查询方案1.Struct & Map查询为空的情况2.FirstOrInit3.FirstOrCreate4.高级查询1.Struct & Map查询为空的情况 当通过结构体进行查询时,GORM将会只通过非零值字段查询,这意味着如果你的字段值为0,‘’,false…...

MFC 简单使用事件
功能三个按钮,一个静态框,默认值是0,增加减少按钮和退出按钮.增加减少按钮显示在静态框中.退出按钮退出软件.实验事件思路新建三个事件,add事件sub事件quit事件,一个按钮触发一个事件,静态框新建一个线程接受事件做出对应的改变.UI添加的代码就不具体说,具体说下事件的代码,这才…...
| 机考必刷)
华为OD机试题 - 端口合并(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:端口合并题目输入输出示例一输入输出说明示例二输入输出说明示例…...
ECharts数据可视化--常用图表类型
目录 一.柱状图 1.基本柱状图 1.1最简单的柱状图 编辑 1.2多系列柱状图 1.3柱状图的样式 (1)柱条样式 (2)柱条的宽度和高度 (3)柱条间距 (4)为柱条添加背景颜色 编辑 2.堆…...
Flutter面试题解析-GridView详解与应用
一、前言Flutter 作为时下最流行的技术之一,凭借其出色的性能以及抹平多端的差异优势,早已引起大批技术爱好者的关注,甚至一些 闲鱼 , 美团 , 腾讯 等大公司均已投入生产使用。虽然目前其生态还没有完全成熟࿰…...

最全的论文写作技巧(建议收藏)
近10年来,笔者有幸多次参与教学论文的评审工作,在此,特将教学论文写作的步骤及相关问题整理汇总如下: 一、选定论题 (一)论题在文中的地位与作用 严格地讲,论文写作是从选定论题开始的。选题…...
)
面向对象设计模式:设计模式分类(创建型、行为型、结构型)
1. 创建型设计模式 单例模式:https://blog.csdn.net/qq_44992559/article/details/129348686工厂模式:https://blog.csdn.net/qq_44992559/article/details/115222311抽象工厂模式:https://blog.csdn.net/qq_44992559/article/details/12934…...

MySQL数据库迁移
考试系统的数据库一直是在我自己的服务器上面的, 但是最近,自己的服务器马上要过期了,里面的MySQL数据需要迁移出来,放在另外一个服务器上面。百度了几篇教程,也没研究太多,选了一种比较简单的方式进行迁移…...
Docker:关于 Dockerfile 编写优化的一些笔记整理
写在前面 分享一些 Dickerfile 构建镜像优化方式的笔记理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃避方式&#…...

个性化营销:您需要知道的信息
个性化营销在现代企业中风靡一时。我们将剖析您需要了解的有关个性化营销的信息,一起来了解一下吧。 什么是个性化营销? 个性化营销是一种一对一营销形式,它使用实时用户数据和分析来传递品牌信息并针对特定潜在客户。 它与传统营销不同&…...

栈和队列的相互实现
文章目录一、用栈实现队列入队:出队:Java代码实现:二、用队列实现栈入栈:出栈:Java代码实现:附:C版代码1、用栈实现队列2、用队列实现栈栈(stack):先进后出&a…...

iTab新标签页重磅更新 |这些功能绝对有你想要的新体验!
01 写在前面 csdn的朋友们,你好哦,我是iTab 插件的独立开发者,今天给大家安利一下我做的这款桌面插件。 首先要告诉大家一个好消息: 最近iTab新标签页被Edge 浏览器商店官方热门🔥推荐啦。 在此,特别感谢…...
【改机教程】iOS系统去除小黑条,改拍照声、拨号音、键盘音,不用越狱,支持所有机型
大家好,上次给大家分享了几个iOS系统免越狱改机教程 今天带来最新的教程,这次修改利用的是同一个漏洞,由外网大神 tamago 开发,国内大神冷风 进行汉化和优化 可以修改的地方包括 去除底部小黑条 dock栏透明 桌面文件夹透明 桌面…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
