期末算法复习
0-1背包问题(动态规划)
例题
算法思想:
动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。
主要是状态转移方程和状态

算法描述:
- 初始化一个二维数组dp,大小为(n+1)×(W+1),其中n为物品的个数,W为背包的容量限制。
- 将dp数组的第0行和第0列全部初始化为0,表示背包容量为0或物品个数为0时的最大总价值都为0。
- 对于物品i,从1到n,依次进行以下操作:
- 对于背包容量j,从1到W,依次进行以下操作:
- 如果第i个物品的重量小于等于背包容量j,则可以选择装入该物品或不装入该物品,选择其中总价值较大的方案:
- 如果选择装入该物品,则总价值为dp[i-1][j-w[i]] + v[i],其中w[i]为第i个物品的重量,v[i]为第i个物品的价值;
- 如果选择不装入该物品,则总价值为dp[i-1][j]。
- 取两者中的较大值作为dp[i][j]的值。
- 如果第i个物品的重量大于背包容量j,则无法选择装入该物品,只能选择不装入该物品,即dp[i][j] = dp[i-1][j]。
- 如果第i个物品的重量小于等于背包容量j,则可以选择装入该物品或不装入该物品,选择其中总价值较大的方案:
- 对于背包容量j,从1到W,依次进行以下操作:
- 最终的dp[n][W]即为问题的解,表示在物品个数为n,背包容量为W时的最大总价值。
复杂度分析:
- 时间复杂度:动态规划解法的时间复杂度为O(nW),其中n为物品的个数,W为背包的容量限制。
- 空间复杂度:动态规划解法的空间复杂度为O(nW),需要使用一个二维数组dp来记录子问题的最优解,若是使用滚动数组优化,可以减小空间复杂度,实际上只用开一维数组,O(W)。
正确性分析:
代码:
// 代码一:
import java.util.Scanner;
public class Main {public static void main(String[] args) {int n, W;int[] v = new int[110], w = new int[110];int[][] dp = new int[110][110];Scanner scanner = new Scanner(System.in);W = scanner.nextInt();n = scanner.nextInt();for(int i = 1; i <= n; i ++ ) {w[i] = scanner.nextInt();v[i] = scanner.nextInt();}for(int i = 0; i <= W; i ++ ) dp[0][i] = 0;for(int i = 1; i <= n; i ++ ) {for(int j = 0; j <= W; j ++ ) {dp[i][j] = dp[i - 1][j];if (j >= w[i]) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - w[i]] + v[i]);}}System.out.println(dp[n][W]);}
}// 代码二:(滚动数组优化)
import java.util.Scanner;// in:
//70 3
//71 100
//69 1
//1 2
public class Main {public static void main(String[] args) {int n, W;int[] v = new int[110], w = new int[110];int[] dp = new int[1010];Scanner scanner = new Scanner(System.in);t = scanner.nextInt();m = scanner.nextInt();for(int i = 1; i <= n; i ++ ) {w[i] = scanner.nextInt();v[i] = scanner.nextInt();}for(int i = 0; i <= W; i ++ ) dp[i] = 0;for(int i = 1; i <= n; i ++ ) {for(int j = W; j >= w[i]; j -- ) {dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);}}System.out.println(dp[W]);}
}单源最短路径dijkstra(贪心)
算法思想:
Dijkstra算法用于求解单源最短路径问题,即从给定的起点到其他所有节点的最短路径。该算法采用贪心的策略,通过逐步扩展已经确定最短路径的节点集合,来逐步求解所有节点的最短路径。
算法描述:
- 初始化:将起点s到所有其他节点的距离设置为无穷大,将起点s到自身的距离设置为0。
- 创建一个优先队列(最小堆)Q,将起点s加入Q。
- while Q不为空:
- 从Q中选择距离最小的节点u,将u从Q中移除。
- 对于u的所有邻接节点v:
- 计算s到v的距离d,即通过u到v的距离加上s到u的距离。
- 如果d小于v当前的距离,则更新v的距离。
- 如果v不在Q中,则将v加入Q。
- 返回起点s到所有其他节点的最短路径。
复杂度分析:
- 时间复杂度:在每次循环中,需要从Q中选择距离最小的节点,这需要O(V)的时间,其中V是顶点的数量。对于每个节点,需要更新其邻接节点的距离,这需要O(E)的时间,其中E是边的数量。因此,总的时间复杂度为O((V + E) * log V),其中log V是从Q中选择最小值的时间复杂度。
- 空间复杂度:需要使用一个大小为V的优先队列来保存节点,以及一个大小为V的数组来保存每个节点的距离。因此,总的空间复杂度为O(V)。
正确性分析:
- Dijkstra算法通过贪心策略来逐步扩展已经确定最短路径的节点集合,从而求解所有节点的最短路径。该算法的正确性基于贪心选择性质,即每次选择距离最小的节点更新其邻接节点的距离,可以保证得到正确的最短路径。
- 此外,Dijkstra算法还需要满足非负权重的条件,即边的权重不能为负数。如果存在负权重的边,则需要使用其他算法,如Bellman-Ford算法。
代码:
// 朴素版:
int dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 1; i <= n; i++){int t = -1;for(int j = 1; j <= n; j++){if(!visited[j] && (t == -1 || dist[j] < dist[t]))t = j;}visited[t] = true;for(int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]);}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}// 堆优化版:用邻接表存
int dijkstra(int s)
{memset(dist, 0x3f, sizeof(dist));dist[s] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义一个小根堆heap.push({0, s}); // 这里显然要根据距离排序while(heap.size()){PII k = heap.top(); // 取不在集合S中距离最短的点heap.pop();int ver = k.second, distance = k.first;if(st[ver]) continue;st[ver] = true;for(int i = h[ver]; i != -1; i = ne[i]){int j = e[i]; // i只是个下标,e中在存的是i这个下标对应的点。if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({ dist[j], j });}}}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
矩阵连乘问题(动态规划)

算法思想:
矩阵链乘法问题是关于如何以最佳方式对一系列矩阵进行乘法计算,以最小化标量乘法操作的次数。为了实现这一目的,常用动态规划来解决。
假设我们有一系列矩阵 ( A_1, A_2, ..., A_n ),其中矩阵 ( A_i ) 的维度为 ( p_{i-1} \times p_i )。我们的目标是找到一种括号化方式,使得计算这些矩阵乘积所需的标量乘法次数最少。
动态规划的基本思想是利用子问题的最优解构造全局最优解。我们定义一个二维数组 ( m[i][j] ) 来表示计算矩阵 ( A_i ) 到 ( A_j ) 之间连乘所需的最小标量乘法次数。
一般只需要最后一个矩阵的列数。
s[i][j]记录了在i到j范围内,使得乘法次数最小的分割点k。
通过递归地划分问题并结合子问题的解,我们可以构建出整个问题的最优解。
算法描述:
复杂度分析:
- 时间复杂度: 外层循环有 (n-1) 次迭代(链长度从2到n),第二个循环有 (n) 次迭代,内循环最多有 (n) 次迭代,因此总的时间复杂度为 (O(n^3))。
- 空间复杂度: 我们需要一个 (n \times n) 的二维数组来存储中间结果,因此空间复杂度为 (O(n^2))。
正确性分析:
-
子问题的定义: 我们定义 (m[i][j]) 为计算矩阵 (A_i) 到 (A_j) 连乘所需的最小标量乘法次数。
-
边界条件: 当只有一个矩阵时,乘法次数为零,即 (m[i][i] = 0)。
-
状态转移方程: 对于 (i \le j),我们尝试所有可能的分割点 (k),计算 (m[i][j]) 的最小值,即
m[i][j] = min{ m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j] }
代码:
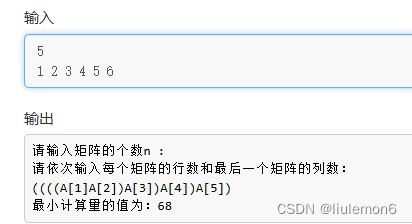
// p[]存放的是所有矩阵的行数和最后一个矩阵的列数
void matrixchain() {memset(m, 0, sizeof(m));memset(s, 0, sizeof(s));//初始化数组for(int r=2; r<=n; r++)//矩阵连乘的规模为r {for(int i=1; i <= n-r+1; i ++ ) // 遍历每一种起点{j = i+r-1;
// 加的认准三个m[i][j]+m[k][w] + p[i - 1] + p[j] + p[w]m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; // 初始假设将所有矩阵都与第一个矩阵相乘s[i][j]=i; // s[][]存储各子问题的决策点,即下标for(int k=i+1; k < j; k++) // 寻找最优值{int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if(t < m[i][j]){m[i][j]=t;s[i][j]=k;}}}}
}
// 决策点用来决定打印的加括号的位置
void print(int i,int j) {if(i == j){cout<<"A["<<i<<"]";return;}cout<<"(";print(i,s[i][j]);print(s[i][j]+1,j);//递归1到s[1][j]cout<<")";
}最长公共子序列(动态规划)

算法思想:
CS问题可以通过动态规划方法来解决。基本思想是使用一个二维数组存储子问题的解,从而避免重复计算。具体步骤如下:
- 定义状态:设
dp[i][j]表示序列X[1..i]和Y[1..j]的最长公共子序列的长度。 - 状态转移方程:
- 如果
X[i] == Y[j],则dp[i][j] = dp[i-1][j-1] + 1; - 如果
X[i] != Y[j],则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
- 如果
- 初始条件:当任何一个序列为空时,最长公共子序列的长度为0,即
dp[i][0] = dp[0][j] = 0。

算法描述:
function LCS(X, Y):
m = length(X)
n = length(Y)
# 创建二维数组 dp
dp = array of size (m+1) x (n+1) initialized to 0
# 填充 dp 表
for i from 1 to m:
for j from 1 to n:
if X[i-1] == Y[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# 返回最终结果
return dp[m][n]
复杂度分析:
时间复杂度
填充一个大小为 (m+1) x (n+1) 的二维数组,每个元素的计算时间为常数时间。因此,总的时间复杂度为 O(m * n),其中 m 和 n 分别是序列 X 和 Y 的长度。
空间复杂度
空间复杂度主要取决于用于存储 dp 数组的空间。二维数组 dp 的大小为 (m+1) x (n+1),所以空间复杂度为 O(m * n)。但是,可以通过空间优化技术(例如使用滚动数组)将空间复杂度降低到 O(min(m, n))。
正确性分析:
基础情况正确性
- 当
i=0或j=0时,dp[i][0]和dp[0][j]都初始化为0,这表示空序列与任何序列的LCS长度为0,这是正确的。
递推关系正确性
- 当
X[i-1] == Y[j-1]时,dp[i][j] = dp[i-1][j-1] + 1,这表示当前字符相等时,最长公共子序列长度增加1。 - 当
X[i-1] != Y[j-1]时,dp[i][j] = max(dp[i-1][j], dp[i][j-1]),这表示要么不包括X[i-1],要么不包括Y[j-1],取两者中较大者作为当前子问题的解。
代码:
#include<iostream>
#include<cstring>
using namespace std;const int N = 1e4 + 10;
string str1, str2;
int c[N][N];
void LCS() {for(int i = 0; i < str1.size(); i ++ ) {for(int j = 0; j < str2.size(); j ++ ) {if(str1[i] == str2[j]) c[i + 1][j + 1] = c[i][j] + 1;else c[i + 1][j + 1] = max(c[i][j + 1], c[i + 1][j]);}}cout << c[str1.size()][str2.size()] << endl;
}int main() {cin >> str1 >> str2;LCS();return 0;
}
作业调度问题(回溯法)
每一个作业Ji都有两项任务分别在2台机器上完成。每个作业必须先有机器1处理,然后再由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理时间。则所有作业在机器2上完成处理时间和f=F2i,称为该作业调度的完成时间和。当作业以相同次序在机器1和机器2上完成处理时,可以得到一种最佳调度,即使该作业调度的完成时间和最小。
算法思想:
对于给定的n个作业,指定最佳作业调度方案,使其完成时间和最小,因此是求一个最优值。
调度必须遵循:
① 一个作业必须先由机器1处理,再由机器2处理,顺序不可颠倒;
② 机器1处理n个作业的顺序必须和机器2处理n个作业的顺序相同(因为只有这样才能使作业调度的完成时间和最小)。
由于是一种作业调度顺序的方案,因此该问题的解空间树是排列树。
算法描述:

复杂度分析:
时间复杂度
- 在最坏情况下,回溯法需要考虑所有可能的解,因此时间复杂度通常为指数级别,即 O(2^n),其中 n 是作业的数量。
- 实际应用中,通过剪枝(约束条件的合理设置)可以显著减少搜索空间,提高效率。
空间复杂度
- 回溯法通常只需要辅助空间来存储当前状态和最优解的临时变量,因此空间复杂度较低,通常为 O(n),其中 n 是作业的数量。
正确性分析:
如何判断某个作业需要在机器2上完成的任务何时开始,这个节点是上一个作业在机器2上完成处理的时间和本作业在机器1上完成处理的时间的较大者
代码:
void Backtrack(int i)
{if(i>n) //每到达一个叶子结点,一定是产生了一个最优解,因此要更新之前最优解的值{if(f<bestf) //更新最优解{for(int j=1;j<=n;j++)bestx[j]=x[j];bestf=f;}}else{for(int j=i;j<=n;j++) //控制展开i-1层结点的各个分支。例如当i=1时,表示在整棵排列树的根结点处,刚要开始探索结点,这时可以展开的分支有1、2、3……{f1+=M[x[j]][1]; //计算第i层(个)作业在机器1上的完成处理的时间if(f2[i-1]>f1) //如果第(i-1)个作业在机器2上的完成处理的时间大于第i个作业在机器1上的完成处理的时间,那么第i个作业想进入机器2,就要等第(i-1)个作业在机器2上完成后再说f2[i]=f2[i-1]+M[x[j]][2];else //否则,第i个作业可以在机器1上完成处理后直接进入机器2。f2[i]=f1+M[x[j]][2];f+=f2[i]; //计算完第i个作业在机器2上的完成处理的时间,就可以计算出前i个作业在机器2上完成处理的时间和了if(f<bestf) //截止到这,已经得到一个前i个作业在机器2上完成处理的时间和f,如果f比之前记录的前i个作业在机器2上的完成处理的时间和的最优值bestf都要小,就可以生成第i层结点的孩子结点,继续探索下一层{Swap(x[i],x[j]); //把处于同一层的并且使f更小的那个结点拿过来,放到正在探索的这个结点处(这里结合排列数的图可以更好地理解)Backtrack(i+1); //继续探索以第i层结点为根结点的子树Swap(x[i],x[j]); //探索完要回溯时,只要做探索前的反“动作”就可以了}f-=f2[i]; //探索完要回溯时,只要做探索前的反“动作”就可以了f1-=M[x[j]][1]; //探索完要回溯时,只要做探索前的反“动作”就可以了}}
}会场安排问题(贪心)
算法思想:
只需要关心开始时间和结束时间,,只要集合里面的最大结束时间和当前的开始时间就可以
算法描述:
假设在足够多的会场里安排一批活动,并希望使用尽可能少的会场。设计一个有效的贪心算法进行安排。
贪心策略:采用结束时间最早的会场作为贪心选择。
2. 用数组 s ss 和 f ff 分别存储各活动的开始时间和结束时间。
将数组 s ss 排序,该次序为各活动选择会场的次序。
将数组 f ff 排序。由于会场的结束时间由活动的结束时间决定,排序后的数组也是会场的结束时间点。
3. (1)先为最早开始的活动开辟一个会场,此时会场的最早结束时间为该活动的结束时间。(2)然后遍历剩下的活动。对于每个活动,判断当前最早结束的会场内是否仍有活动:如果有,开辟一个新会场;如果没有,说明当前最早结束的会场能容纳当前的活动,更新会场的结束时间点,保证最早结束的会场最先开始下一个活动。
复杂度分析:
时间复杂度:O(nlogn) 排序
空间复杂度:O(n)
正确性分析:
代码:
#include <iostream>
#include <algorithm>
using namespace std;
//5
//1 23
//12 28
//25 35
//27 80
//36 50
const int N = 1e5 + 10;
int n;
struct hd{int a, b;
}h[N];
bool cmp(hd h1, hd h2) {return h1.a < h2.a;
}
int main() {cin >> n;for(int i = 0; i < n; i ++ ) cin >> h[i].a >> h[i].b;sort(h, h + n, cmp);int res = -1;for(int i = 0; i < n; i ++ ) {int j = i + 1, t = 1;while(h[j].a < h[i].b && j < n) {t ++;j ++;}res = max(res, t);}cout << res << endl;return 0;
}// 贪心正解:
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cout<<"请输入活动的个数:"<<endl;cin>>n;int s[n],f[n];cout<<"请输入每个活动的开始时间和结束时间:"<<endl;for(int i=0;i<n;i++){cin>>s[i]>>f[i];}sort(s,s+n);//理解一下为什么都要升序 sort(f,f+n);//会场的最短结束时间次序用j来表示,待分配的活动按i来遍历 int j=0,ans=0;for(int i=0;i<n;i++){if(s[i] < f[j]){ans++;}else{j++;}} cout<<"最小会场数是:"<<ans<<endl; return 0;
}
图m着色问题(回溯法)
算法思想:
算法尝试所有可能的染色方案,并使用剪枝操作减少无效搜索,最终输出染色方案的数量。
算法描述:
设图G=(V, E), |V|=n, 颜色数= m, 用邻接矩阵a表示G, 用整数1, 2…m来表示
m种不同的颜色。顶点i所着的颜色用x[i]表示。
问题的解向量可以表示为n元组x={ x[1],…,x[n] }. x[i]∈{1,2,…,m},
解空间树为排序树,是一棵n+1层的完全m叉树.
在解空间树中做深度优先搜索, 约束条件:如果g[j][i]=1 , x[i] ≠ x[j]
复杂度分析:
- 时间复杂度:O(m^n)
- 空间复杂度:O(N^2)
正确性分析:
代码:
一颗排列树,一般时间为O(n!)
#include <iostream>
using namespace std;const int N = 1e4 + 10;
int m, n, edgenum;
int x[N], g[N][N];
int ans;int check(int i) {for(int j = 1; j < i; j ++ ) {if(g[i][j] && x[i] == x[j]) return false;}return true;
}void dfs(int u) {if(u > n) {ans ++;for(int i = 1; i <= n; i ++ ) {cout << x[i] << ' ';}cout << endl;return ;}else {for(int i = 0; i < m; i ++ ) {x[u] = i;if(check(u))dfs(u + 1);x[u] = 0;}}
}int main() {cin >> n >> m >> edgenum;for(int i = 0; i < edgenum; i ++ ) {int a, b;cin >> a >> b;g[a][b] = g[b][a] = 1;}dfs(1);if(ans) cout << "染色方案的数量为:" << ans << endl;else cout << "无染色方案" << endl; return 0;
}// 优化
#include <iostream>
#include <vector>
using namespace std;const int N = 1e4 + 10;
int m, n, edgenum;
int x[N];
vector<int> g[N];
int ans;bool check(int i) {for (int j : g[i]) {if (x[i] == x[j]) return false;}return true;
}void dfs(int u) {if (u > n) {ans++;for (int i = 1; i <= n; i++) {cout << x[i] << ' ';}cout << endl;return;}for (int i = 0; i < m; i++) {x[u] = i;if (check(u)) {dfs(u + 1);}x[u] = -1; // 重置状态}
}int main() {cin >> n >> m >> edgenum;for (int i = 0; i < edgenum; i++) {int a, b;cin >> a >> b;g[a].push_back(b);g[b].push_back(a);}fill(x, x + N, -1); // 初始化颜色数组为-1dfs(1);if (ans)cout << "染色方案的数量为:" << ans << endl;elsecout << "无染色方案" << endl;return 0;
}
旅行售货员问题tsp(回溯法)
算法思想:
它通过递归搜索所有可能的路径,并在每一步进行剪枝(分支限界)来减少不必要的计算,尝试找到最短的环路。其实就是寻找哈密尔顿回路
算法描述:
- 递归终止条件:当
u == citynum时,表示已经访问所有城市,此时需要检查是否可以回到起点并更新最优成本。 - 循环和交换:在每一步中,尝试将当前步的节点与后续节点进行交换以生成不同的路径。
- 剪枝条件:如果当前路径的成本加上从前一个城市到当前城市的成本小于当前已知的最优成本,则继续搜索。
复杂度分析:
- 时间复杂度: ( O(n!) )
- 空间复杂度: ( O(n) )
正确性分析:
代码:
同样是一个排序树
void BackTrack(int u) { // u指的是第u步 if(u == citynum) { // 此时是叶子结点的父节点 if(Graph[x[u - 1]][x[u]] != NoEdge && Graph[x[u]][1] != NoEdge && (Graph[x[u - 1]][x[u]] + Graph[x[u]][1] + currentcost < bestcost || bestcost == max_)) {bestcost = Graph[x[u - 1]][x[u]] + Graph[x[u]][1] + currentcost;for(int i = 1; i <= citynum; i ++ ) {bestx[i] = x[i];}}return;}else {for(int j = u; j <= citynum; j ++ ) {if(Graph[x[u - 1]][x[j]] != NoEdge && Graph[x[u - 1]][x[j]] + currentcost < bestcost || bestcost == max_) { // 分支和界限 swap(x[u], x[j]);currentcost += Graph[x[u - 1]][x[u]];BackTrack(u + 1);currentcost -= Graph[x[u - 1]][x[u]];swap(x[u], x[j]);}}}
}N皇后问题(回溯法)
算法思想:
任意两个皇后都不能处于同一行、同一列或同一斜线上。可以把八皇后问题扩展到n皇后问题,即在n×n的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。

算法描述:
回溯法,解空间树是一个排序树
复杂度分析:
时间复杂度O(n!)
空间复杂度O(n^2)
正确性分析:
代码:dg主对角线,+n防止负值,udg副对角线不会有负值
#include <iostream>
using namespace std;const int N = 1010;
int n, ans;
int g[N][N];
int col[N], dg[N], udg[N];void dfs(int u) {if(u > n) {ans ++;for(int i = 1; i <= n ; i++ ) {for(int j = 1; j <= n; j ++ ) {if(g[i][j]) {cout << "q ";}else cout << ". ";}cout << endl;}cout << endl;return ;}else {for(int i = 1; i <= n; i ++ ) {if(!col[i] && !dg[i - u + n] && !udg[i + u]) {col[i] = 1;dg[i - u + n] = 1;udg[i + u] = 1;g[u][i] = 1;dfs(u + 1);g[u][i] = 0;col[i] = 0;dg[i - u + n] = 0;udg[i + u] = 0;}}}
}int main() {cin >> n;dfs(1);cout << ans << endl;return 0;
}KMP算法(字符串)
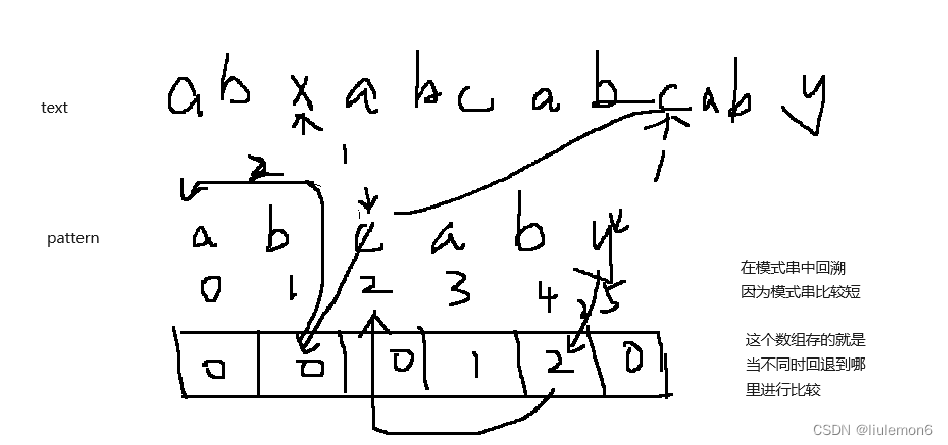
算法思想:
找出模式串在文本串中的出现位置,暴力解法两个循环O(mn)
kmp算法,不用在文本串中回溯了。空间复杂度O(n),时间复杂度O(m+n)
算法描述:
复杂度分析:
正确性分析:
代码:
#include <iostream>using namespace std;const int N = 100010, M = 10010; //N为模式串长度,M匹配串长度int n, m;
int ne[M];
char s[N], p[M]; //s为模式串, p为匹配串int main()
{cin >> n >> s+1 >> m >> p+1; //下标从1开始//求next[]数组for(int i = 2, j = 0; i <= m; i++){while(j && p[i] != p[j+1]) j = ne[j];if(p[i] == p[j+1]) j++;ne[i] = j;}//匹配操作for(int i = 1, j = 0; i <= n; i++){while(j && s[i] != p[j+1]) j = ne[j]; // 回溯if(s[i] == p[j+1]) j++;if(j == m) // 满足匹配条件,打印开头下标, 从0开始{//匹配完成后的具体操作//如:输出以0开始的匹配子串的首字母下标//printf("%d ", i - m); (若从1开始,加1)j = ne[j]; //再次继续匹配}}return 0;
}相关文章:

期末算法复习
0-1背包问题(动态规划) 例题 算法思想: 动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。 主要是状态转移方程和状态 算法描述: 初始化一个二维数组dp࿰…...

可穿戴设备:苹果“吃老底”、华为“忙复苏”、小米“再扩容”
配图来自Canva可画 随着产品功能的创新,可穿戴设备不再被简单地视为手机的延伸,而是被当成一种独立的、具有独特功能和优势的产品,受到了越来越多人的青睐。 一方面,技术的进步使得可穿戴设备在功能、性能和使用体验上得到显著提…...

AI数据分析:集中度分析和离散度分析
在deepseek中输入提示词: 你是一个Python编程专家,要完成一个Python脚本编写的任务,具体步骤如下: 读取Excel表格:"F:\AI自媒体内容\AI行业数据分析\toolify月榜\toolify2023年-2024年月排行榜汇总数据.xlsx&qu…...

redis的分布式session和本地的session有啥区别
在web应用开发中,Session用于在多个请求之间存储用户数据。传统上,Session存储在服务器的内存中,即本地Session。然而,随着应用规模和复杂度的增加,特别是在分布式环境中,本地Session会遇到一些问题。这时&…...

SSH概念、用途、详细使用方法
还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas,webgl,ech…...
关于电脑文件的规划思考
概述 设置C、D、E、F 四个盘 C盘:系统数据使用,操作系统、其他软件需要用到的系统性资源 D盘:应用软件区 的使用,数据库、navacat、idea、visual studio、浏览器、向日葵、虚拟机…… E盘:工作区:公司资料…...
DVWA - Brute Force
DVWA - Brute Force 等级:low 直接上bp弱口令爆破,设置变量,攻击类型最后一个,payload为用户名、密码简单列表 直接run,长度排序下,不一样的就是正确的用户名和密码 另解: 看一下…...
安卓手机文件找回方法汇总,3个技巧,不再焦虑
我们用手机来储存各种重要的信息和文件,无论是珍贵的照片、重要的文档还是喜爱的音乐,用来记录和分享生活中的每一个瞬间。但如果不小心删除了这些文件,我们可能会面临数据丢失的风险,进而产生焦虑和不安。本文将为您揭秘手机文件…...

{}初始化
文章目录 ()初始化的问题易混淆弱检查 {}初始化{}初始化是c11推荐的初始化,解决了上述的问题 ()则被用于强制类型转换 ()初始化的问题 易混淆 string s();不能确定是函数定义还是对象定义 弱检查 int a(3.14);3.14 可以通过 int 定义 {}初始化 {}初始化是c11推…...

小程序外卖开发中的关键技术与实现方法
小程序外卖服务凭借其便捷性和灵活性,正成为现代餐饮行业的重要组成部分。开发一个功能完善的小程序外卖系统,需要掌握一系列关键技术和实现方法。本文将介绍小程序外卖开发中的核心技术,并提供具体的代码示例,帮助开发者理解和实…...

大数据平台之运维管理工具
大数据平台的自动化运维管理工具能够大幅提升集群管理效率,减少人为错误,提高系统的稳定性和性能。这些工具通常提供集群监控、配置管理、自动化任务执行、安全管理和故障处理等功能。以下是一些主要的大数据平台自动化运维管理工具的详细介绍࿱…...

[vue3]组件通信
自定义属性 父组件中给子组件绑定属性, 传递数据给子组件, 子组件通过props选项接收数据 props传递的数据, 在模版中可以直接使用{{ message }}, 在逻辑中使用props.message defineProps defineProps是编译器宏函数, 就是一个编译阶段的标识, 实际编译器解析时, 遇到后会进行…...
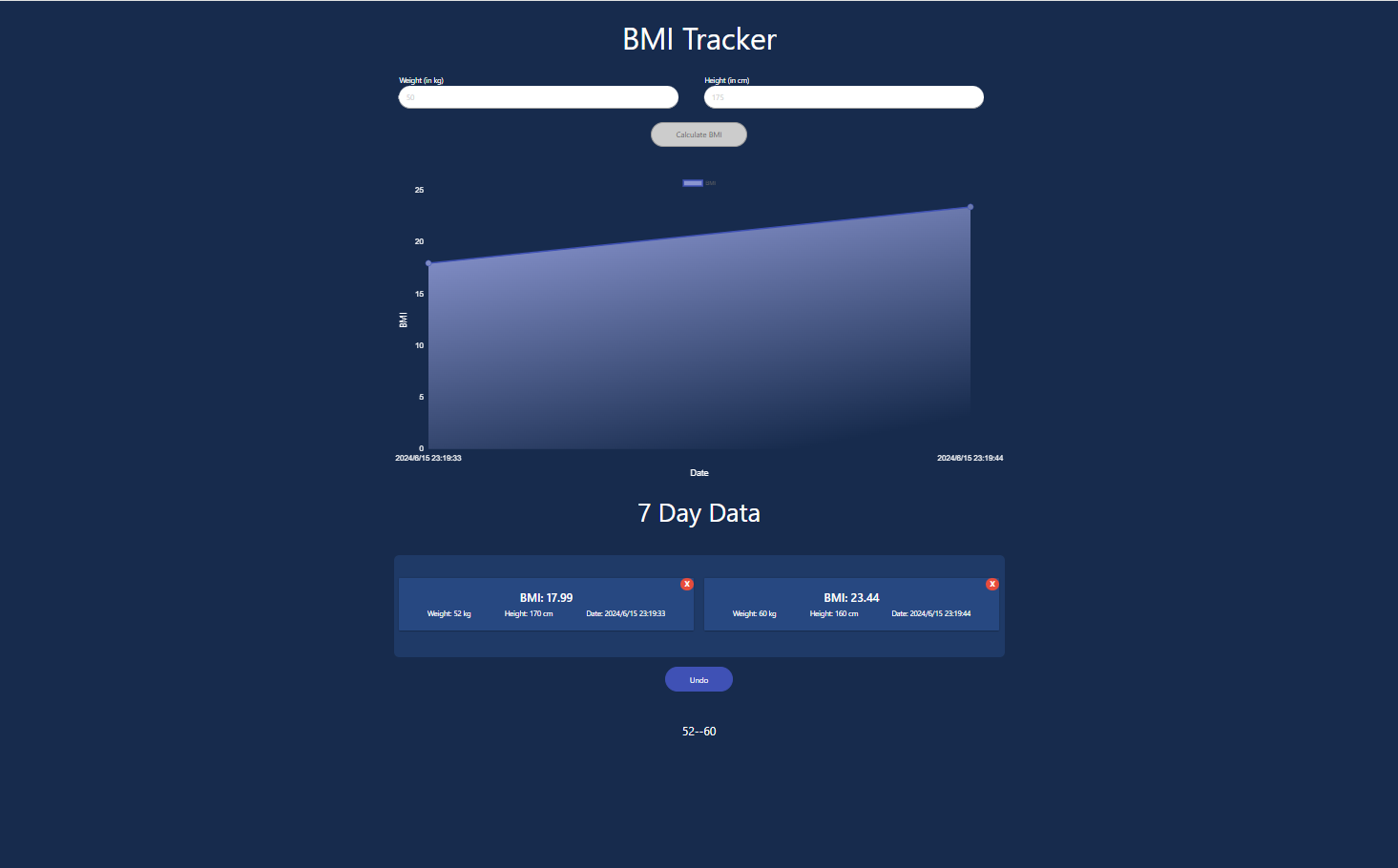
【react小项目】bmi-calculator
bmi-calculator 目录 bmi-calculator初始化项目01大致布局01代码 02完善样式02代码 03输入信息模块03代码 04 使用图表04代码 05详细记录信息渲染05代码 06 让数据变成响应式的06-1输入框的数据处理06-2图表,和记录信息的区域数据处理 07 删除功能,撤销功…...

python判断一个数是不是偶数
在Python中,你可以使用模运算符 % 来判断一个数是否为偶数。模运算符会返回两个数相除的余数。如果一个数除以2的余数为0,那么这个数就是偶数。 以下是一个简单的Python函数,用于判断一个数是否为偶数: def is_even(n):return n…...
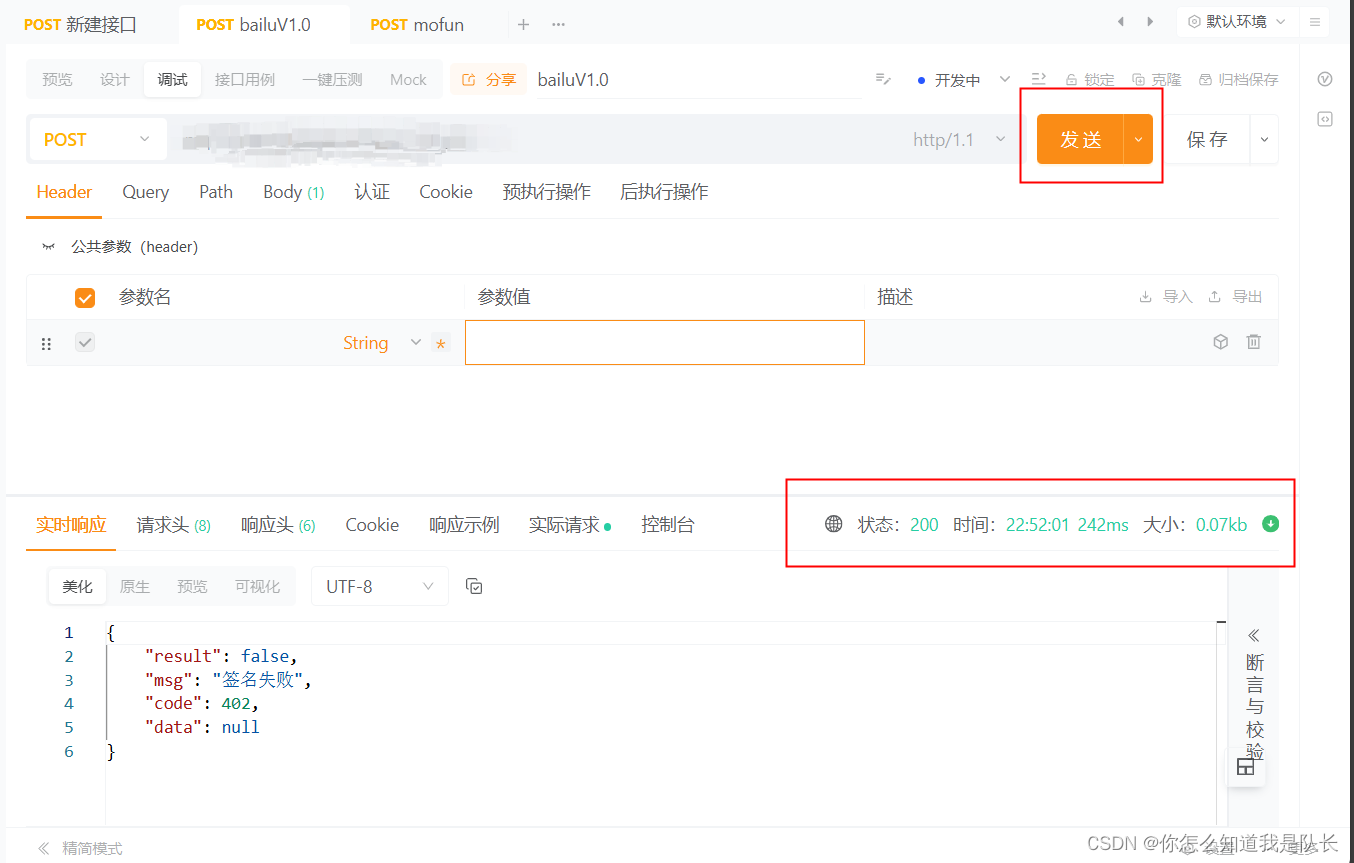
Apipost模拟HTTP客户端
模拟HTTP客户端的软件有很多,其中比较著名的就有API-FOX、POSTMAN。 相信很多小伙伴都使用POSTMAN。这篇博客主要介绍Apipost的原因是,Apipost无需下载,具有网页版。 APIFOX的站内下载: Api-Fox,类似于PostMan的软件…...
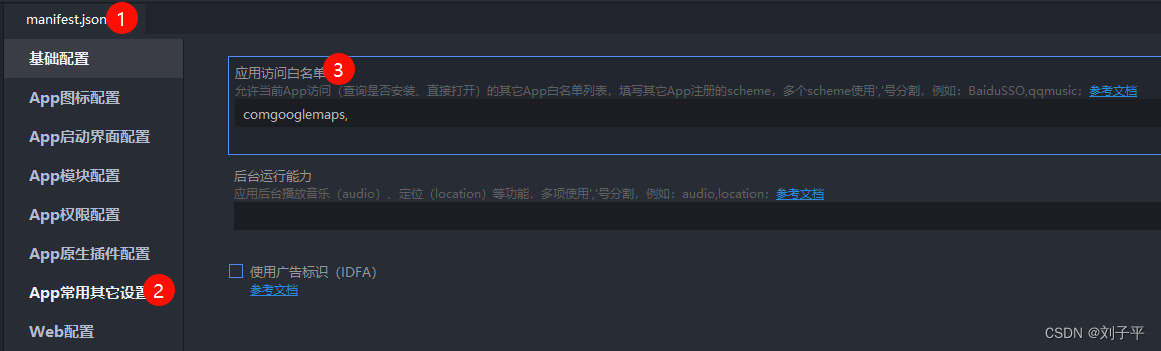
uniapp 调用手机上安装的app (高德地图 百度地图 Apple地图 谷歌地图)
uniapp 调用手机上安装的app (高德地图 百度地图 Apple地图 谷歌地图) 效果 思路 获取手机类型(安卓/iOS)let platform uni.getSystemInfoSync().platform判断手机有没有安装需要的应用plus.runtime.isApplicationExist({action: ""}))打开应用 跳转过去plus.runt…...

如果供应商不能按时交货怎么办?
虽然说我们在采购的时候,我们会和供应商签订合同,合同上也会注明交期时间等一些必需的条件。 但是当供货商真的没有如期交货,或者交货拖延的时候,我们第一时间选择的是拿起法律武器来让对方承担违约责任吗? 显然,这选…...
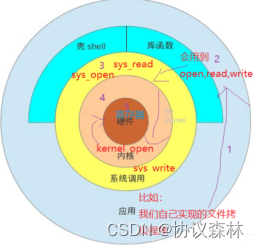
【Linux应用】Linux系统的设备管理——Udev
1.udev概述 udev是 Linux2.6内核里的一个功能,它替代了原来的 devfs,成为当前 Linux 默认的设备管理工具,能够根据系统中的硬件设备的状态动态更新设备文件,包括设备文件的创建,删除等。 udev以守护进程的形式运行&am…...

超实用!给独立开发者福音的一站式应用开发工具!
各位开发者们,是否曾经为了搭建服务、开发接口API而头痛不已?是否曾因为需要集成各种第三方认证服务而感到心力交瘁?别担心,今天我要向大家介绍的是一款专为“懒人”开发者准备的神器——MemFire Cloud。这款一站式应用开发工具不…...

华为 HarmonyOS 中国市场份额一季度超越苹果 iOS
华为 HarmonyOS 中国市场份额一季度超越苹果 iOS 根据最新发布的数据,研究机构Counterpoint Research指出,在2024年第一季度,华为的操作系统HarmonyOS在中国市场超越了苹果的iOS,成为中国市场上的第二大操作系统。 
在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
