Java高级编程技术详解:从多线程到算法优化的全面指南
复杂度与优化
复杂度与优化在算法中的应用
算法复杂度是衡量算法效率的重要指标。了解和优化算法复杂度对提升程序性能非常关键。本文将介绍时间复杂度和空间复杂度的基本概念,并探讨一些优化技术。
时间复杂度和空间复杂度
时间复杂度表示算法执行所需时间随输入规模变化的情况,通常用大O符号表示。常见的时间复杂度有O(1)、O(log n)、O(n)、O(n log n)、O(n²)等。
空间复杂度表示算法运行过程中占用的存储空间,常见的空间复杂度有O(1)、O(n)等。
示例代码:计算一个数组中最大值的时间复杂度
public class MaxValue {/*** 找到数组中的最大值* @param arr 输入数组* @return 数组中的最大值*/public static int findMax(int[] arr) {int max = arr[0]; // 假设第一个元素是最大值for (int value : arr) { // 遍历数组if (value > max) {max = value; // 更新最大值}}return max;}public static void main(String[] args) {int[] numbers = {1, 3, 5, 7, 9};System.out.println("Max value: " + findMax(numbers)); // 输出最大值}
}
上述代码的时间复杂度为O(n),空间复杂度为O(1)。
优化技术
- 减少不必要的计算:在循环中避免重复计算,尽量将不变的计算移出循环。
- 使用高效的数据结构:如哈希表、堆等,这些数据结构能在某些情况下显著降低时间复杂度。
示例代码:使用哈希表优化查找
import java.util.HashMap;
import java.util.Map;public class FindPair {/*** 判断数组中是否存在两个元素的和等于目标值* @param arr 输入数组* @param target 目标和* @return 如果存在这样的元素,返回true;否则返回false*/public static boolean hasPairWithSum(int[] arr, int target) {Map<Integer, Integer> map = new HashMap<>();for (int num : arr) { // 遍历数组if (map.containsKey(target - num)) {return true; // 找到一对满足条件的元素}map.put(num, 1); // 记录当前元素}return false; // 没有找到满足条件的元素}public static void main(String[] args) {int[] numbers = {1, 3, 5, 7, 9};int target = 8;System.out.println("Pair with sum " + target + ": " + hasPairWithSum(numbers, target)); // 输出是否存在满足条件的元素}
}
上述代码的时间复杂度为O(n),空间复杂度为O(n)。
并行与分布式算法
Java中的并行与分布式算法
并行和分布式算法在处理大规模数据和高性能计算中起到关键作用。本文将介绍Java中的并行处理技术和MapReduce算法。
并行算法
Java提供了多种并行处理的工具,包括java.util.concurrent包和Fork/Join框架。
示例代码:Fork/Join框架
import java.util.concurrent.RecursiveTask;
import java.util.concurrent.ForkJoinPool;public class SumTask extends RecursiveTask<Integer> {private final int[] arr;private final int start, end;/*** 构造函数,初始化待处理的数组区间* @param arr 输入数组* @param start 起始位置* @param end 结束位置*/public SumTask(int[] arr, int start, int end) {this.arr = arr;this.start = start;this.end = end;}@Overrideprotected Integer compute() {if (end - start <= 10) { // 如果任务规模小于等于10,则直接计算int sum = 0;for (int i = start; i <= end; i++) {sum += arr[i];}return sum;} else { // 否则分解任务int mid = (start + end) / 2;SumTask leftTask = new SumTask(arr, start, mid);SumTask rightTask = new SumTask(arr, mid + 1, end);leftTask.fork(); // 异步执行左子任务return rightTask.compute() + leftTask.join(); // 等待左子任务执行完毕并合并结果}}public static void main(String[] args) {int[] numbers = new int[100];for (int i = 0; i < 100; i++) {numbers[i] = i + 1;}ForkJoinPool pool = new ForkJoinPool();int sum = pool.invoke(new SumTask(numbers, 0, numbers.length - 1)); // 提交任务给ForkJoinPool执行System.out.println("Sum: " + sum); // 输出求和结果}
}
分布式算法
MapReduce是一种分布式算法,用于处理大规模数据集。
示例代码:简单MapReduce实现
import java.util.*;
import java.util.stream.Collectors;public class SimpleMapReduce {/*** Map阶段,统计文档中的单词频率* @param documents 输入文档数组* @return 单词频率的映射*/public static Map<String, Integer> map(String[] documents) {Map<String, Integer> wordCount = new HashMap<>();for (String doc : documents) {String[] words = doc.split("\\s+");for (String word : words) {wordCount.put(word, wordCount.getOrDefault(word, 0) + 1);}}return wordCount;}/*** Reduce阶段,合并所有映射中的单词频率* @param maps 单词频率映射的列表* @return 合并后的单词频率映射*/public static Map<String, Integer> reduce(List<Map<String, Integer>> maps) {Map<String, Integer> finalCount = new HashMap<>();for (Map<String, Integer> map : maps) {for (Map.Entry<String, Integer> entry : map.entrySet()) {finalCount.put(entry.getKey(), finalCount.getOrDefault(entry.getKey(), 0) + entry.getValue());}}return finalCount;}public static void main(String[] args) {String[] docs = {"hello world", "hello java", "java concurrency"};List<Map<String, Integer>> maps = Arrays.stream(docs).map(SimpleMapReduce::map).collect(Collectors.toList());Map<String, Integer> result = reduce(maps);result.forEach((k, v) -> System.out.println(k + ": " + v)); // 输出合并后的单词频率}
}
图算法
Java中的高级图算法
图算法在解决诸如网络流、最短路径等问题时非常有用。本文将介绍一些高级图算法及其Java实现。
网络流算法
最大流算法用于计算网络中的最大流量。Ford-Fulkerson方法是一种经典的最大流算法。
示例代码:Ford-Fulkerson算法
import java.util.LinkedList;
import java.util.Queue;public class FordFulkerson {private static final int V = 6; // 图中的顶点数/*** 使用广度优先搜索查找增广路径* @param rGraph 残余图* @param s 源点* @param t 汇点* @param parent 存储路径的数组* @return 如果存在增广路径,返回true;否则返回false*/boolean bfs(int[][] rGraph, int s, int t, int[] parent) {boolean[] visited = new boolean[V];Queue<Integer> queue = new LinkedList<>();queue.add(s);visited[s] = true;parent[s] = -1;while (!queue.isEmpty()) {int u = queue.poll();for (int v = 0; v < V; v++) {if (!visited[v] && rGraph[u][v] > 0) {queue.add(v);parent[v] = u;visited[v] = true;}}}return visited[t];}/*** 使用Ford-Fulkerson算法计算最大流量* @param graph 输入图* @param s 源点* @param t 汇点* @return 最大流量*/int fordFulkerson(int[][] graph, int s, int t) {int[][] rGraph = new int[V][V]; // 残余图for (int u = 0; u < V; u++) {for (int v = 0; v < V; v++) {rGraph[u][v] = graph[u][v];}}int[] parent = new int[V];int maxFlow = 0;while (bfs(rGraph, s, t, parent)) {int pathFlow = Integer.MAX_VALUE;for (int v = t; v != s; v = parent[v]) {int u = parent[v];pathFlow = Math.min(pathFlow, rGraph[u][v]);}for (int v = t; v != s; v = parent[v]) {int u = parent[v];rGraph[u][v] -= pathFlow;rGraph[v][u] += pathFlow;}maxFlow += pathFlow;}return maxFlow;}public static void main(String[] args) {int[][] graph = {{0, 16, 13, 0, 0, 0},{0, 0, 10, 12, 0, 0},{0, 4, 0, 0, 14, 0},{0, 0, 9, 0, 0, 20},{0, 0, 0, 7, 0, 4},{0, 0, 0, 0, 0, 0}};FordFulkerson ff = new FordFulkerson();System.out.println("Maximum flow: " + ff.fordFulkerson(graph, 0, 5)); // 输出最大流量}
}
最短路径算法
Dijkstra算法用于计算图中从源点到其他顶点的最短路径。
示例代码:Dijkstra算法
import java.util.Arrays;
import java.util.PriorityQueue;public class Dijkstra {private static final int V = 9;/*** 使用Dijkstra算法计算最短路径* @param graph 输入图* @param src 源点*/void dijkstra(int[][] graph, int src) {int[] dist = new int[V];boolean[] sptSet = new boolean[V];Arrays.fill(dist, Integer.MAX_VALUE);dist[src] = 0;PriorityQueue<Node> pq = new PriorityQueue<>(V, (a, b) -> a.cost - b.cost);pq.add(new Node(src, 0));while (!pq.isEmpty()) {int u = pq.poll().vertex;sptSet[u] = true;for (int v = 0; v < V; v++) {if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v]) {dist[v] = dist[u] + graph[u][v];pq.add(new Node(v, dist[v]));}}}printSolution(dist);}/*** 打印最短路径结果* @param dist 最短路径数组*/void printSolution(int[] dist) {System.out.println("Vertex\tDistance from Source");for (int i = 0; i < V; i++) {System.out.println(i + "\t" + dist[i]);}}public static void main(String[] args) {int[][] graph = {{0, 4, 0, 0, 0, 0, 0, 8, 0},{4, 0, 8, 0, 0, 0, 0, 11, 0},{0, 8, 0, 7, 0, 4, 0, 0, 2},{0, 0, 7, 0, 9, 14, 0, 0, 0},{0, 0, 0, 9, 0, 10, 0, 0, 0},{0, 0, 4, 14, 10, 0, 2, 0, 0},{0, 0, 0, 0, 0, 2, 0, 1, 6},{8, 11, 0, 0, 0, 0, 1, 0, 7},{0, 0, 2, 0, 0, 0, 6, 7, 0}};Dijkstra dijkstra = new Dijkstra();dijkstra.dijkstra(graph, 0); // 从源点0计算最短路径}class Node {int vertex;int cost;public Node(int vertex, int cost) {this.vertex = vertex;this.cost = cost;}}
}
机器学习与深度学习
Java中的机器学习与深度学习
机器学习和深度学习在现代数据分析中非常重要。本文将介绍如何在Java中实现简单的神经网络,以及如何使用DL4J进行深度学习。
简单的神经网络
一个简单的神经网络可以通过矩阵运算实现。
示例代码:简单的神经网络实现
import java.util.Random;public class SimpleNeuralNetwork {private final double[][] weights;/*** 构造函数,初始化神经网络的权重* @param inputSize 输入层大小* @param outputSize 输出层大小*/public SimpleNeuralNetwork(int inputSize, int outputSize) {weights = new double[inputSize][outputSize];Random rand = new Random();for (int i = 0; i < inputSize; i++) {for (int j = 0; j < outputSize; j++) {weights[i][j] = rand.nextDouble();}}}/*** 预测函数,计算输出* @param inputs 输入数据* @return 输出数据*/public double[] predict(double[] inputs) {double[] outputs = new double[weights[0].length];for (int i = 0; i < weights[0].length; i++) {outputs[i] = 0;for (int j = 0; j < weights.length; j++) {outputs[i] += inputs[j] * weights[j][i];}}return outputs;}public static void main(String[] args) {SimpleNeuralNetwork nn = new SimpleNeuralNetwork(3, 2);double[] inputs = {1.0, 0.5, -1.0};double[] outputs = nn.predict(inputs);for (double output : outputs) {System.out.println(output);}}
}
使用DL4J进行深度学习
DL4J(Deeplearning4j)是Java中流行的深度学习库。下面的代码展示了如何使用DL4J训练一个简单的神经网络。
示例代码:使用DL4J进行深度学习
import org.deeplearning4j.datasets.iterator.impl.MnistDataSetIterator;
import org.deeplearning4j.nn.api.OptimizationAlgorithm;
import org.deeplearning4j.nn.conf.MultiLayerConfiguration;
import org.deeplearning4j.nn.conf.NeuralNetConfiguration;
import org.deeplearning4j.nn.conf.layers.DenseLayer;
import org.deeplearning4j.nn.conf.layers.OutputLayer;
import org.deeplearning4j.nn.multilayer.MultiLayerNetwork;
import org.deeplearning4j.optimize.api.IterationListener;
import org.deeplearning4j.optimize.listeners.ScoreIterationListener;
import org.nd4j.linalg.api.ndarray.INDArray;
import org.nd4j.linalg.dataset.api.iterator.DataSetIterator;
import org.nd4j.linalg.factory.Nd4j;
import org.nd4j.linalg.learning.config.Sgd;
import org.nd4j.linalg.lossfunctions.LossFunctions;public class DL4JExample {public static void main(String[] args) throws Exception {int inputSize = 784;int outputSize = 10;int batchSize = 128;int epochs = 5;DataSetIterator mnistTrain = new MnistDataSetIterator(batchSize, true, 12345);MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder().seed(123).optimizationAlgo(OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT).updater(new Sgd(0.1)).list().layer(new DenseLayer.Builder().nIn(inputSize).nOut(1000).activation("relu").build()).layer(new OutputLayer.Builder(LossFunctions.LossFunction.NEGATIVELOGLIKELIHOOD).nIn(1000).nOut(outputSize).activation("softmax").build()).build();MultiLayerNetwork model = new MultiLayerNetwork(conf);model.init();model.setListeners(new ScoreIterationListener(10));for (int i = 0; i < epochs; i++) {model.fit(mnistTrain);}// 评估模型性能DataSetIterator mnistTest = new MnistDataSetIterator(batchSize, false, 12345);Evaluation eval = new Evaluation(outputSize);while (mnistTest.hasNext()) {DataSet ds = mnistTest.next();INDArray output = model.output(ds.getFeatureMatrix());eval.eval(ds.getLabels(), output);}System.out.println(eval.stats());}
}
相关文章:

Java高级编程技术详解:从多线程到算法优化的全面指南
复杂度与优化 复杂度与优化在算法中的应用 算法复杂度是衡量算法效率的重要指标。了解和优化算法复杂度对提升程序性能非常关键。本文将介绍时间复杂度和空间复杂度的基本概念,并探讨一些优化技术。 时间复杂度和空间复杂度 时间复杂度表示算法执行所需时间随输…...

Redis 分布式锁过期了,还没处理完怎么办?
为了防止死锁,我们会给分布式锁加一个过期时间,但是万一这个时间到了,我们业务逻辑还没处理完,怎么办? 这是一个分布式应用里很常见到的需求,关于这个问题,有经验的程序员会怎么处理呢ÿ…...

Vue2+Element-ui后台系统常用js方法
el-dialog弹框关闭清空form表单并清空验证 cancelDialog(diaLog, formRef) {this[diaLog] falseif (formRef) {this.$refs[formRef].resetFields()} }页面使用: <el-dialog :visible.sync"addSubsidyDialog.dialog" close"cancelDialog(addSub…...

Kafka高频面试题整理
文章目录 1、什么是Kafka?2、kafka基本概念3、工作流程4、Kafka的数据模型与消息存储机制1)索引文件2)数据文件 5、ACKS 机制6、生产者重试机制:7、kafka是pull还是push8、kafka高性能高吞吐的原因1)磁盘顺序读写:保证了消息的堆积2)零拷贝机…...

uniapp地图自定义文字和图标
这是我的结构: <map classmap id"map" :latitude"latitude" :longitude"longitude" markertap"handleMarkerClick" :show-location"true" :markers"covers" /> 记住别忘了在data中定义变量…...

k8s_探针专题
关于探针 生产环境中一定要给pod设置探针,不然pod内的应用发生异常时,K8s将不会重启pod。 需要遵循以下几个原则(本人自己总结,仅供参考): 探针尽量简单,不要消耗过多资源。因为探针较为频繁的…...

MySQL触发器基本结构
1、修改分隔符符号 delimiter $$ 可以修改成$$ //都行 2、创建触发器函数名称 create trigger 函数名 3、什么样的操作出发,操作那个表 after:......之后触发 befor:......之前触发 insert:插入被触发 update:修改被触…...

前缀和(一维前缀和+二维前缀和)
前缀和 定义: 前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。 用途: 前缀和一般用于统计一个区间的和&…...

web前端五行属性:深入探索与实战解析
web前端五行属性:深入探索与实战解析 在Web前端开发中,五行属性这一概念或许听起来有些陌生。然而,如果我们将其与前端开发的核心理念相结合,就能发现其中蕴含的深刻内涵。本文将从四个方面、五个方面、六个方面和七个方面&#…...

白酒:茅台镇白酒的酒厂社会责任与可持续发展
云仓酒庄豪迈白酒,作为茅台镇的品牌,不仅在产品品质和口感方面有着卓着的表现,在酒厂社会责任和可持续发展方面也做出了积极的探索和实践。 首先,云仓酒庄豪迈白酒注重环境保护和资源利用。酒厂在生产过程中严格控制能源消耗和排放…...

音视频开发_SDL音频播放器的实现
今天向大家介绍一下如何通过 SDL 实现一个PCM音频播放器。这是一个最简单的播放器,它不涉及到音频的解复用,解码等工作。我们只需要将音频原始数据喂给 SDL 音频接口就可以听到悦耳的声音了。在下面的列子中我将向你演示,使用 SDL 做这样一个…...
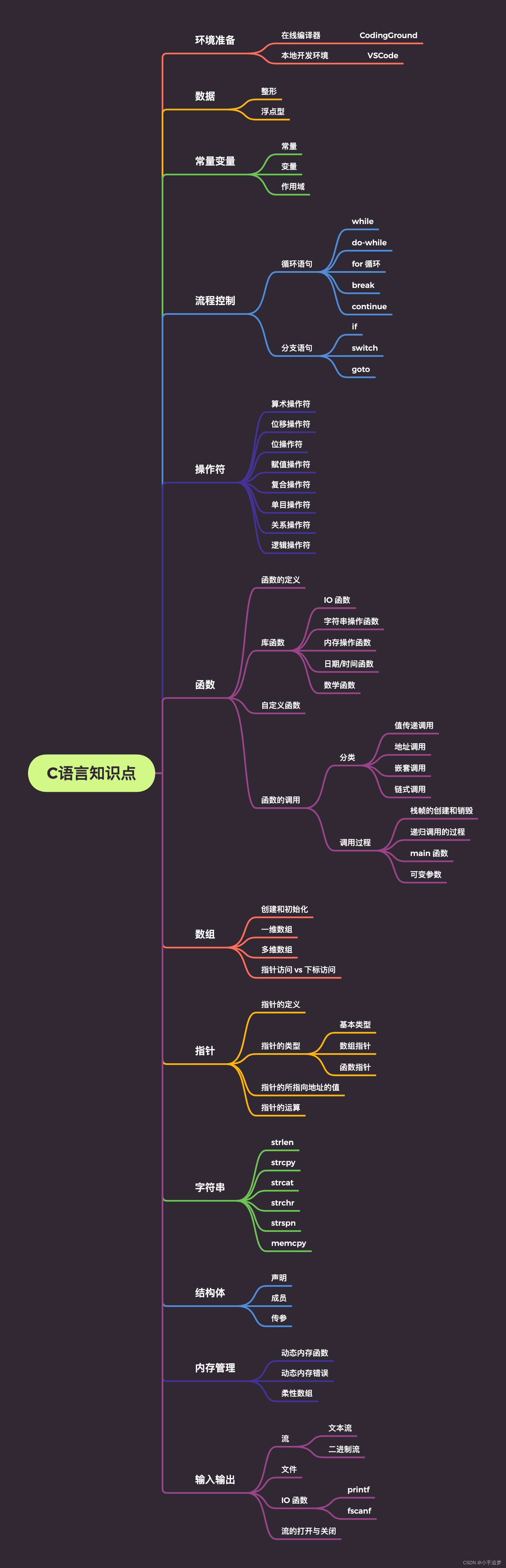
C语言学习系列:初识C语言
前言,C语言是什么 语言,比如中文、英语、法语、德语等,是人与人交流的工具。 C语言也是语言,不过是一种特殊的语言,是人与计算机交流的工具。 为什么叫C语言呢? 这就要从C语言的历史说起了。 一&#…...
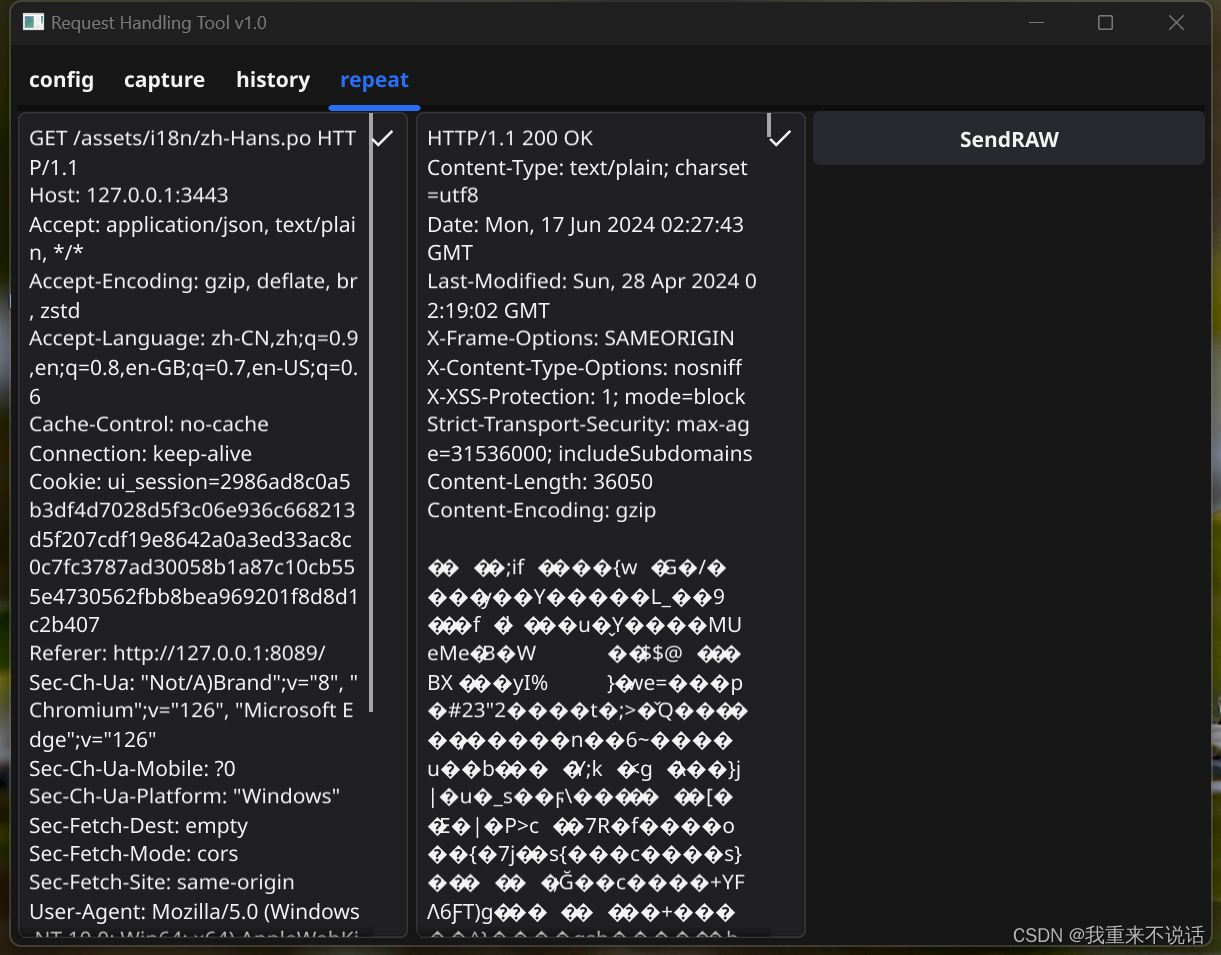
利用反向代理编写HTTP抓包工具——可视化界面
手写HTTP抓包工具——可视化界面 项目描述语言golang可视化fynev2功能代理抓包、重发、记录 目录 1. 示例1.1 主界面1.2 开启反向代理1.3 抓包1.4 历史记录1.5 重发 2. 核心代码2.1 GUI2.1 抓包 3. 结语3.1 传送门 1. 示例 1.1 主界面 1.2 开启反向代理 1.3 抓包 1.4 历史记录…...

下拉框数据被遮挡 且 后续数据无法下拉的 解决方法
目录 前言1. 问题所示2. 原理分析3. 解决方法3.1 添加空白版2.2 调整z-index2.3 父容器的溢出属性2.4 调整样式属性4. 效果图前言 小程序使用的是Uniapp,原理都差不多,索性标题就不标注Uniapp(小程序) 对于该问题调试了一个晚上,最终解决,对此记录下来 1. 问题所示 执…...

课设--学生成绩管理系统(二)
欢迎来到 Papicatch的博客 目录 🐋引言 🦈编写目的 🦈项目说明 🐋产品介绍 🦈产品概要说明 🦈产品用户定位 🦈产品中的角色 🐋 产品总体业务流程图 🐋 产品功…...

STM32CubeMX配置-外部中断配置
一、简介 MCU为STM32G070,配置为上升沿触发外部中断,在上升沿外部中断回调函数中进行相关操作。 二、外部中断配置 查看规格书中管教描述,找到I/O对应的外部中断线,然后进行如下上升沿触发外部中断配置。 三、生成代码 调用上升沿…...

基于Vue的日程排班表 - common-schedule
原文:基于Vue的日程排班表 - common-schedule-CSDN博客...
SmartEDA、Multisim、Proteus大比拼:电路设计王者之争?
在电路设计领域,SmartEDA、Multisim和Proteus无疑是三款备受瞩目的软件工具。它们各自拥有独特的功能和优势,但在这场电路设计王者的竞争中,谁才是真正的领跑者?让我们深入探究这三款软件的异同,揭示它们各自的魅力所在…...

【教资科一传统文化】文化素养传统文化之神话传说、天文历法、古代称谓、中国传统节日、成语典故
目录 编辑 传统文化之天文历法 (一)四时(四季)从农历、名称上掌握 (二)二十四节气(1、名称2、季节-节气3、特殊) (三)十二时辰(1.先后顺序2.时间段3.别称) (四)五更(五夜) (五)天干地支(1.名称2.纪年) 文化素养传统文化…...
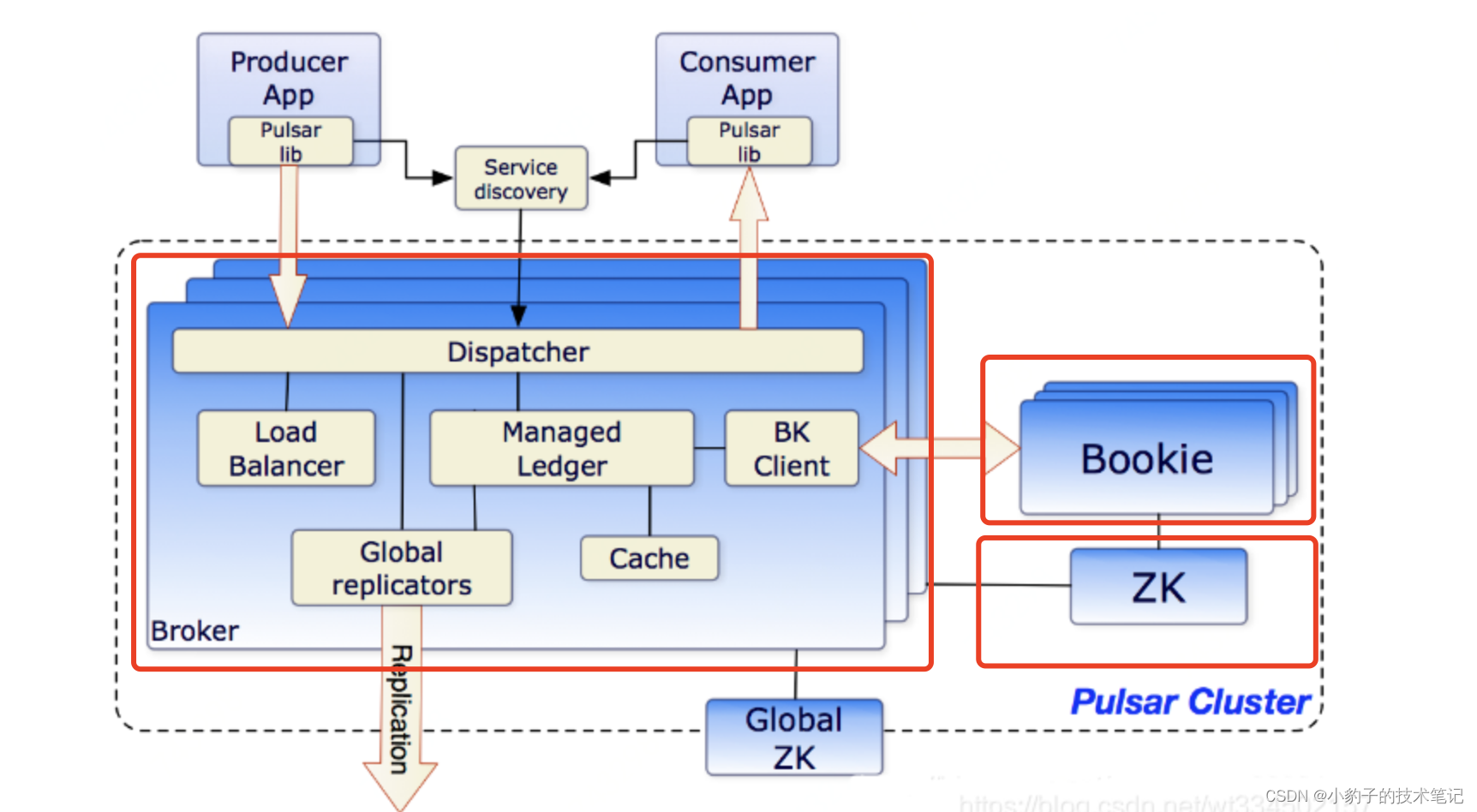
Apache Pulsar 从入门到精通
一、快速入门 Pulsar 是一个分布式发布-订阅消息平台,具有非常灵活的消息模型和直观的客户端 API。 最初由 Yahoo 开发,在 2016 年开源,并于2018年9月毕业成为 Apache 基金会的顶级项目。Pulsar 已经在 Yahoo 的生产环境使用了三年多&#…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
