算法训练营 day43 动态规划 不同路径 不同路径 II
算法训练营 day43 动态规划 不同路径 不同路径 II
不同路径
62. 不同路径 - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径
按照动规五部曲来分析:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
- 举例推导dp数组
class Solution {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}
不同路径 II
63. 不同路径 II - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
62.不同路径 中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了。
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
- dp数组如何初始化
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
- 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
- 举例推导dp数组
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];for (int i = 0; i < m&&obstacleGrid[i][0]==0; i++) dp[i][0] = 1;for (int j = 0; j < n&&obstacleGrid[0][j]==0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j]==1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}
相关文章:

算法训练营 day43 动态规划 不同路径 不同路径 II
算法训练营 day43 动态规划 不同路径 不同路径 II 不同路径 62. 不同路径 - 力扣(LeetCode) 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达…...

关联查询的SQL有几种情况
1、内连接:inner join … on 结果:A表 ∩ B表 2、左连接:A left join B on (2)A表全部 (3)A表- A∩B 3、右连接:A right join B on (4)B表全部 &#…...

查缺补漏三:事务隔离级别
什么是事务? 事务就是一组操作的集合,事务将整组操作作为一个整体,共同提交或者共同撤销 这些操作只能同时成功或者同时失败,成功即可提交事务,失败就执行事务回滚 MySQL的事务默认是自动提交的,一条语句执…...

没有她的通讯录(C语言实现)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石. 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:夏目的C语言宝藏 💬总结:希望你看完之…...

Spring Security 从入门到精通
前言 Spring Security 是 Spring 家族中的一个安全管理框架。相比与另外一个安全框架Shiro,它提供了更丰富的功能,社区资源也比Shiro丰富。 一般来说中大型的项目都是使用SpringSecurity 来做安全框架。小项目有Shiro的比较多,因为相比与Spr…...
微信小程序Springboot vue停车场车位管理系统
系统分为用户和管理员两个角色 用户的主要功能有: 1.用户注册和登陆系统 2.用户查看系统的公告信息 3.用户查看车位信息,在线预约车位 4.用户交流论坛,发布交流信息,在线评论 5.用户查看地图信息,在线导航 6.用户查看个…...
看完这篇 教你玩转渗透测试靶机vulnhub——Hack Me Please: 1
Vulnhub靶机Hack Me Please: 1渗透测试详解Vulnhub靶机介绍:Vulnhub靶机下载:Vulnhub靶机安装:Vulnhub靶机漏洞详解:①:信息收集:②:漏洞利用③:获取反弹shell:④&#x…...
nodejs+vue地铁站自动售票系统-火车票售票系统vscode
地铁站自动售票系统主要包括个人中心、地铁线路管理、站点管理、购票信息管理、乘坐管理、用户信息管理等多个模块。它使用的是前端技术:nodejsvueelementui 前后端通讯一般都是采取标准的JSON格式来交互。前端技术:nodejsvueelementui,视图层其实质就是…...
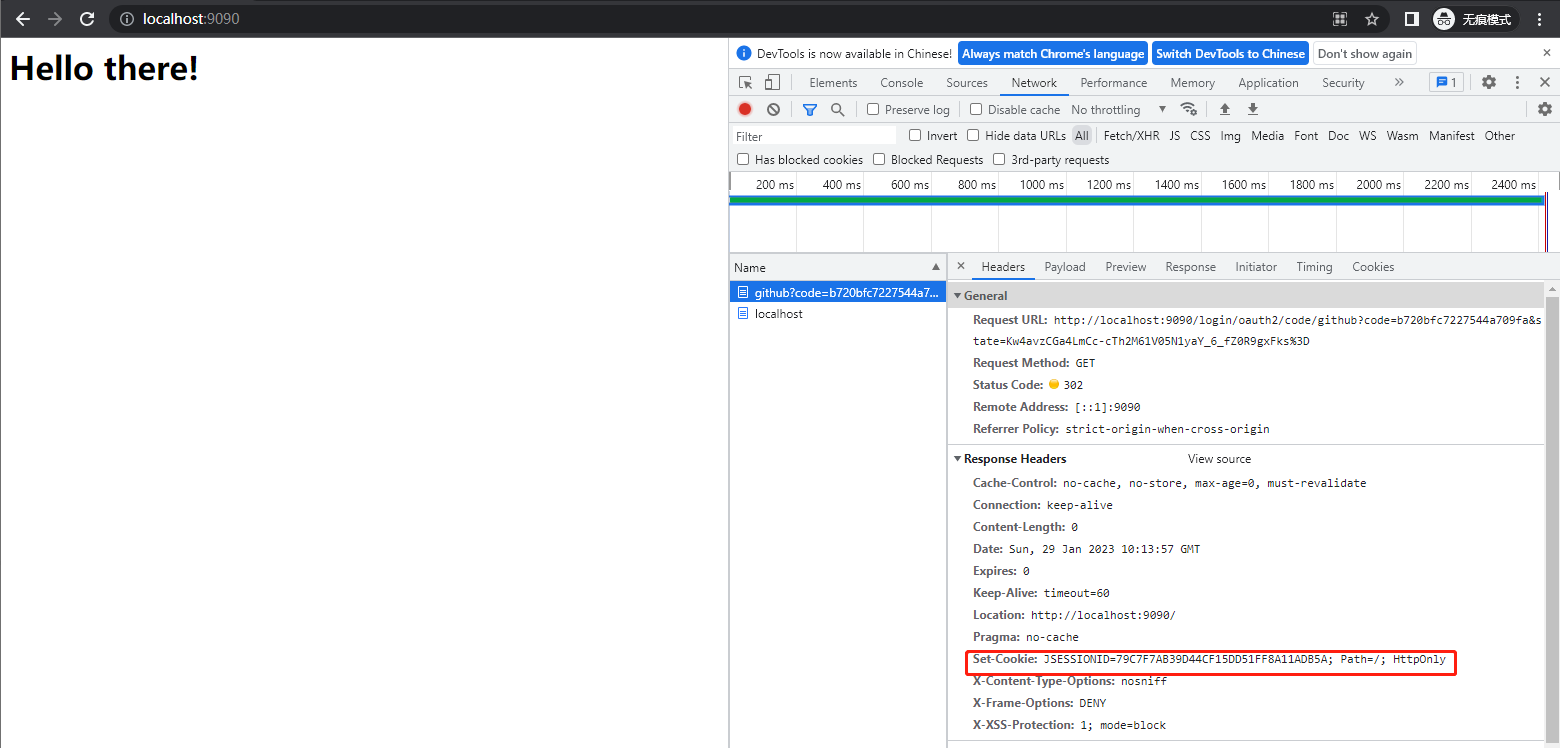
Spring Security in Action 第十二章 OAuth 2是如何工作的?
本专栏将从基础开始,循序渐进,以实战为线索,逐步深入SpringSecurity相关知识相关知识,打造完整的SpringSecurity学习步骤,提升工程化编码能力和思维能力,写出高质量代码。希望大家都能够从中有所收获&#…...
天工开物 #5 我的 Linux 开发机
首先说一下结论:最终我选择了基于 Arch Linux[1] 的 Garuda Linux[2] 发行版作为基础来搭建自己的 Linux 开发机。Neofetch 时刻发行版的选择在上周末的这次折腾里,我一共尝试了 Garuda Linux 发行版,原教旨的 Arch Linux 发行版,…...
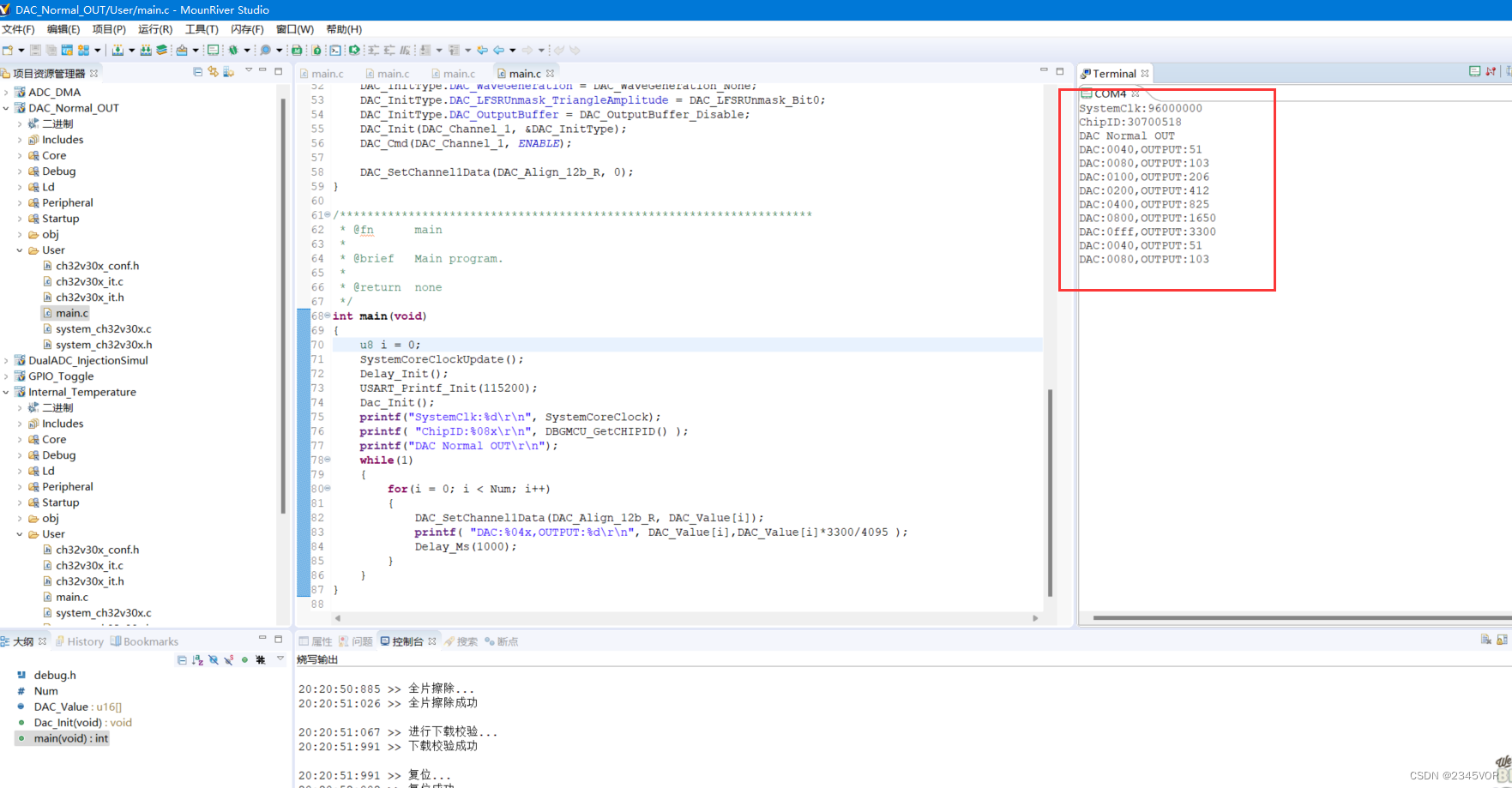
【沁恒WCH CH32V307V-R1开发板输出DAC实验】
【沁恒WCH CH32V307V-R1开发板输出DAC实验】1. 前言2. 软件配置2.1 安装MounRiver Studio3. DAC项目测试3.1 打开DAC工程3.2 编译项目4. 下载验证4.1 接线4.2 演示效果5. 小结1. 前言 数字/模拟转换模块(DAC),包含 2 个可配置 8/12 位数字输入…...
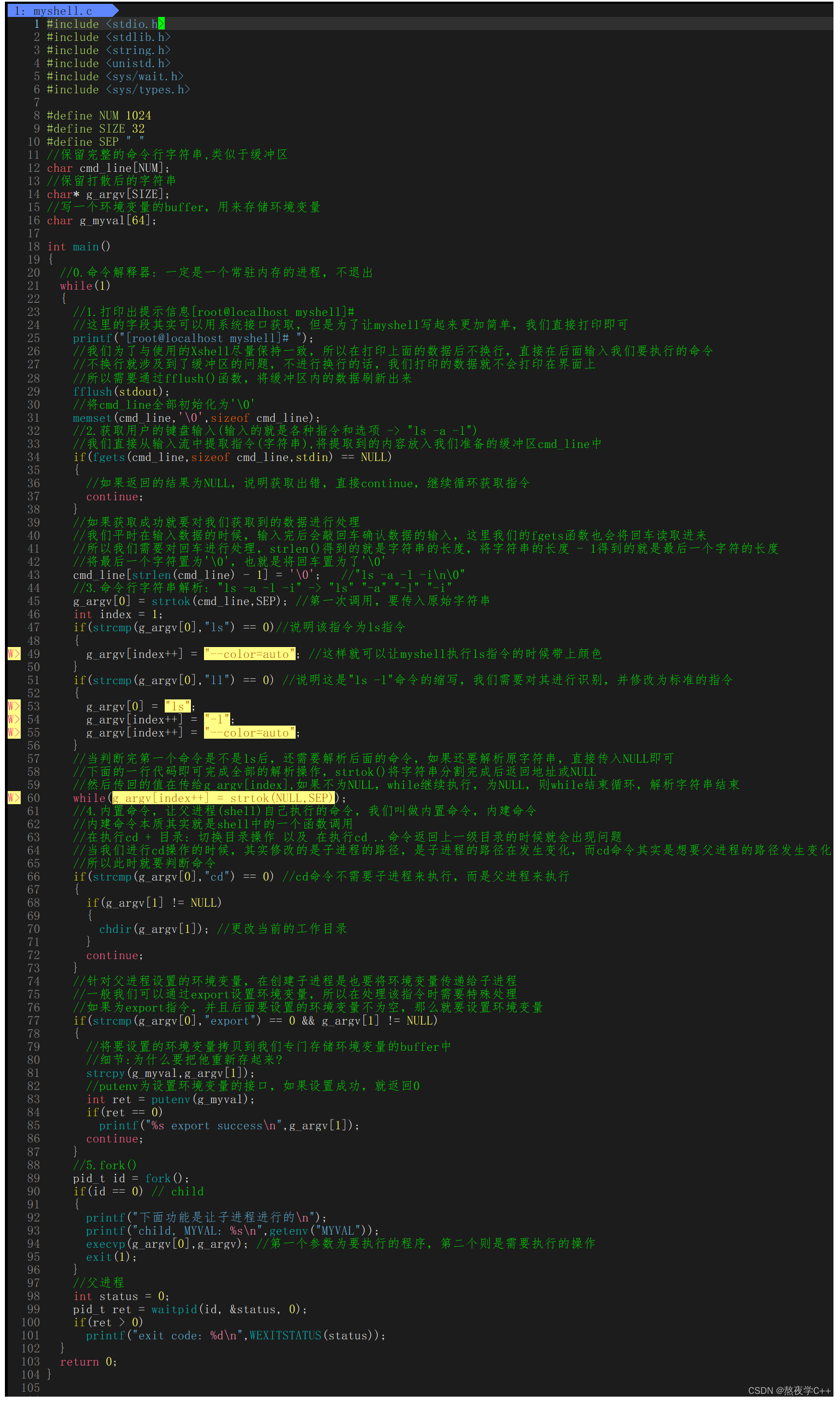
Linux进程控制详解
目录前言一、进程创建1.1 fork函数初识1.2 写时拷贝1.3 fork常规用法1.4 fork调用失败的原因二、进程终止2.1 进程终止时,操作系统做了什么??2.2 进程终止的常见方式有哪些??2.3 如何用代码终止一个进程三、进程等待3.…...

C语言深度剖析之程序环境和预处理
1.程序的翻译环境和执行环境 第一种是翻译环境,在这个环境中源代码被转换为可执行的机器指令 第二种是执行环境,它用于实际执行代码 2.翻译环境 分为四个阶段 预编译阶段 ,编译,汇编,链接 程序编译过程:多个…...
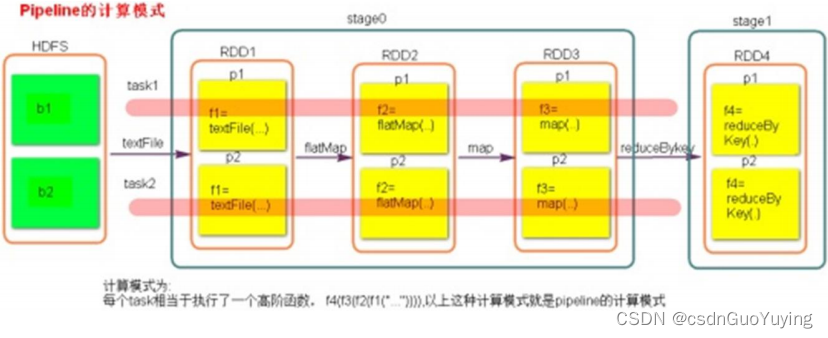
【Spark分布式内存计算框架——Spark Core】9. Spark 内核调度(上)
第八章 Spark 内核调度 Spark的核心是根据RDD来实现的,Spark Scheduler则为Spark核心实现的重要一环,其作用就是任务调度。Spark的任务调度就是如何组织任务去处理RDD中每个分区的数据,根据RDD的依赖关系构建DAG,基于DAG划分Stag…...
: Graphics pipeline之Render passes(渲染通道))
Vulkan教程(15): Graphics pipeline之Render passes(渲染通道)
Vulkan官方英文原文: https://vulkan-tutorial.com/Drawing_a_triangle/Graphics_pipeline_basics/Render_passes对应的Vulkan技术规格说明书版本: Vulkan 1.3.2Setup设置Before we can finish creating the pipeline, we need to tell Vulkan about the…...
乐观锁、雪花算法、MyBatis-Plus多数据源
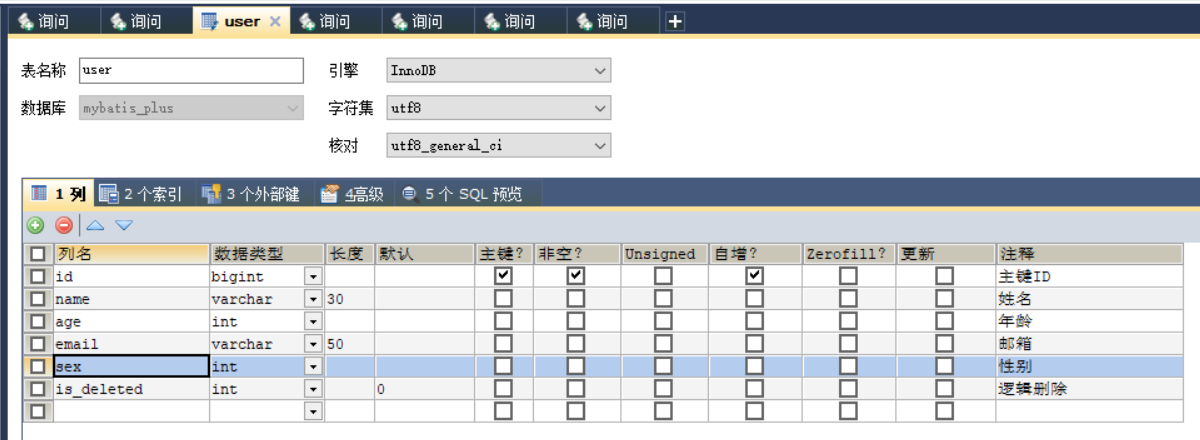
乐观锁、雪花算法、MyBatis-Plus多数据源e>雪花算法2、乐观锁a>场景b>乐观锁与悲观锁c>模拟修改冲突d>乐观锁实现流程e>Mybatis-Plus实现乐观锁七、通用枚举a>数据库表添加字段sexb>创建通用枚举类型c>配置扫描通用枚举d>测试九、多数据源1、创建…...
详解Redisson分布式限流的实现原理
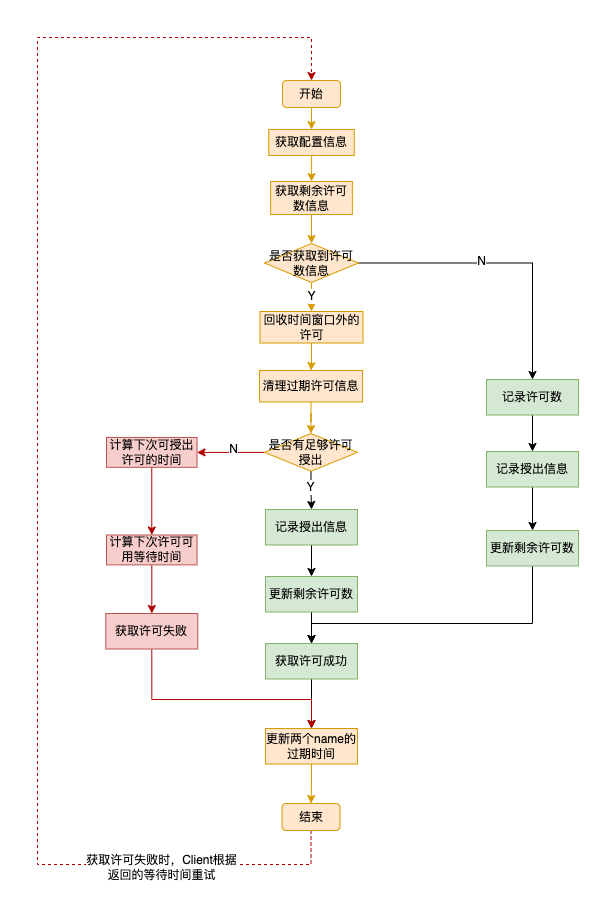
我们目前在工作中遇到一个性能问题,我们有个定时任务需要处理大量的数据,为了提升吞吐量,所以部署了很多台机器,但这个任务在运行前需要从别的服务那拉取大量的数据,随着数据量的增大,如果同时多台机器并发…...

[python入门㊹] - python测试类
目录 ❤ 断言方法 assertEqual 和 assertNotEqual assertTrue 和 assertFalse assertIsNone 和 assertIsNotNone ❤ 一个要测试的类 ❤ 测试AnonymousSurvey类 ❤ setUp() 和 teardown() 方法 ❤ 断言方法 常用的断言方法: 方法 用途 assertEqual(a, b) 核实a …...
Web 框架 Flask 快速入门(二)表单
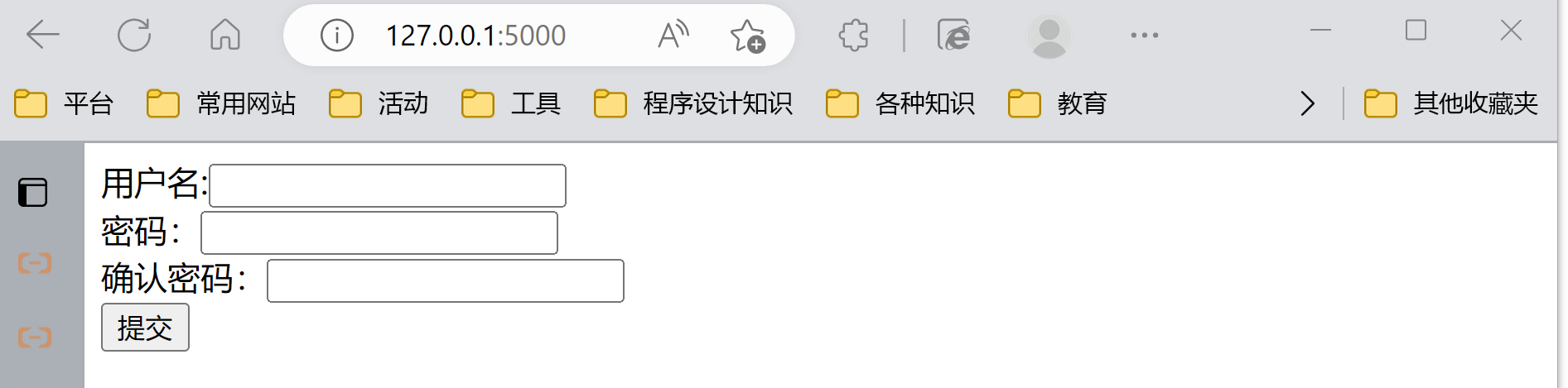
课程地址:Python Web 框架 Flask 快速入门 文章目录🌴 表单1、表单介绍2、表单的简单实现1. 代码2. 代码的执行逻辑3、使用wtf扩展实现4、bug记录:表单验证总是失败🌴 表单 1、表单介绍 当我们在网页上填写账号密码进行登录的时…...

C++基础(5) - 复合类型(上)
文章目录数组1、什么是数组2、数组的声明3、数组的初始化4、数组的访问5、二维数组6、memset —— 给数组中每一个元素赋同样的值字符串(字符数组)1、string.h 头文件1.1 strlen()1.2 strcmp()1.3 strcpy()1.4 strcat()string 类简介1、C11 字符串初始化…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...

安宝特方案丨从依赖经验到数据驱动:AR套件重构特种装备装配与质检全流程
在高压电气装备、军工装备、石油测井仪器装备、计算存储服务器和机柜、核磁医疗装备、大型发动机组等特种装备生产型企业,其产品具有“小批量、多品种、人工装配、价值高”的特点。 生产管理中存在传统SOP文件内容缺失、SOP更新不及、装配严重依赖个人经验、产品装…...

安宝特案例丨寻医不再长途跋涉?Vuzix再次以AR技术智能驱动远程医疗
加拿大领先科技公司TeleVU基于Vuzix智能眼镜打造远程医疗生态系统,彻底革新患者护理模式。 安宝特合作伙伴TeleVU成立30余年,沉淀医疗技术、计算机科学与人工智能经验,聚焦医疗保健领域,提供AR、AI、IoT解决方案。 该方案使医疗…...
