代码随想录算法训练营第39天|● 62.不同路径 ●63. 不同路径 II
不同路径
62. 不同路径 - 力扣(LeetCode)
1.确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2.确定递推公式
p[i][j] = dp[i - 1][j] + dp[i][j - 1]
3.dp数组的初始化
先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理
4.遍历顺序
行列从前到后
class Solution {public int uniquePaths(int m, int n) {int[][]dp=new int[m+1][n+1];for (int i = 1; i <=m ; i++) {dp[i][1]=1;}for (int i = 1; i <=n ; i++) {dp[1][i]=1;}for (int i = 2; i <=m ; i++) {for (int j = 2; j <=n ; j++) {dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
}不同路径II
63. 不同路径 II - 力扣(LeetCode)
与上题不同的是在初始化的时候要保存障碍物的地方要dp[i][j]==0
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m=obstacleGrid.length;int n=obstacleGrid[0].length;int [][]dp=new int[m][n];for (int i = 0; i <m&&obstacleGrid[i][0]==0 ; i++) {dp[i][0]=1;}for (int i = 0; i <n&&obstacleGrid[0][i]==0 ; i++) {dp[0][i]=1;}for (int i = 1; i <m ; i++) {for (int j = 1; j <n ; j++) {if(obstacleGrid[i][j]==1){continue;}else {dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}return dp[m-1][n-1];}
}相关文章:

代码随想录算法训练营第39天|● 62.不同路径 ●63. 不同路径 II
不同路径 62. 不同路径 - 力扣(LeetCode) 1.确定dp数组(dp table)以及下标的含义 dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。 2.确定递推公式 …...

【DevOps】 什么是容器 - 一种全新的软件部署方式
目录 引言 一、什么是容器 二、容器的工作原理 三、容器的主要特性 四、容器技术带来的变革 五、容器技术的主要应用场景 六、容器技术的主要挑战 七、容器技术的发展趋势 引言 在过去的几十年里,软件行业经历了飞速的发展。从最初的大型机时代,到后来的个人电脑时代,…...
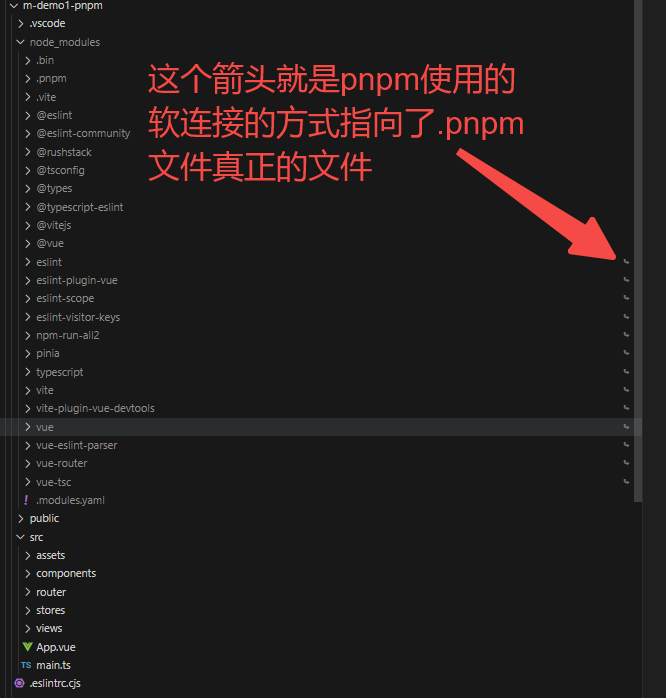
使用pnpm创建vue3项目
https://pnpm.io/zh/ 全局安装: npm install -g pnpm 检查版本: pnpm -v 创建vue3项目: pnpm create vuelatest 项目装包: pnpm install 运行项目: pnpm dev 命令行: https://pnpm.io/zh/pnpm-cli pnpm …...

【软件测试】43个功能测试点总结
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 功能测试就是对产品的各功能进行验证,根据功能测试用例,逐项测试…...

Python — — GPU编程
Python — — GPU编程 要想将Python程序运行在GPU上,我们可以使用numba库或者使用cupy库来实现GPU编程。 壹、numba Numba 是一个开源的 JIT (Just-In-Time) 编译器,它可以将 Python 代码转换成机器代码以提高性能。Numba 特别适用于需要高性能计算的…...

C#中的枚举类-自定义属性
在实际开发过程中,我们常常会用到枚举类,使用枚举的时候往往有着各种使用条件,如何给枚举加入使用条件呢? 答案就是我们的——自定义属性 废话不多说,上代码 枚举类 首先我们要有一个枚举类 public enum XXXX枚举…...

多态深度剖析
前言 继承是多态的基础, 如果对于继承的知识还不够了解, 可以去阅读上一篇文章 继承深度剖析 基本概念与定义 概念: 通俗来说,就是多种形态。具体点就是去完成某个行为, 当不同的对象去完成时会产生出不同的状…...
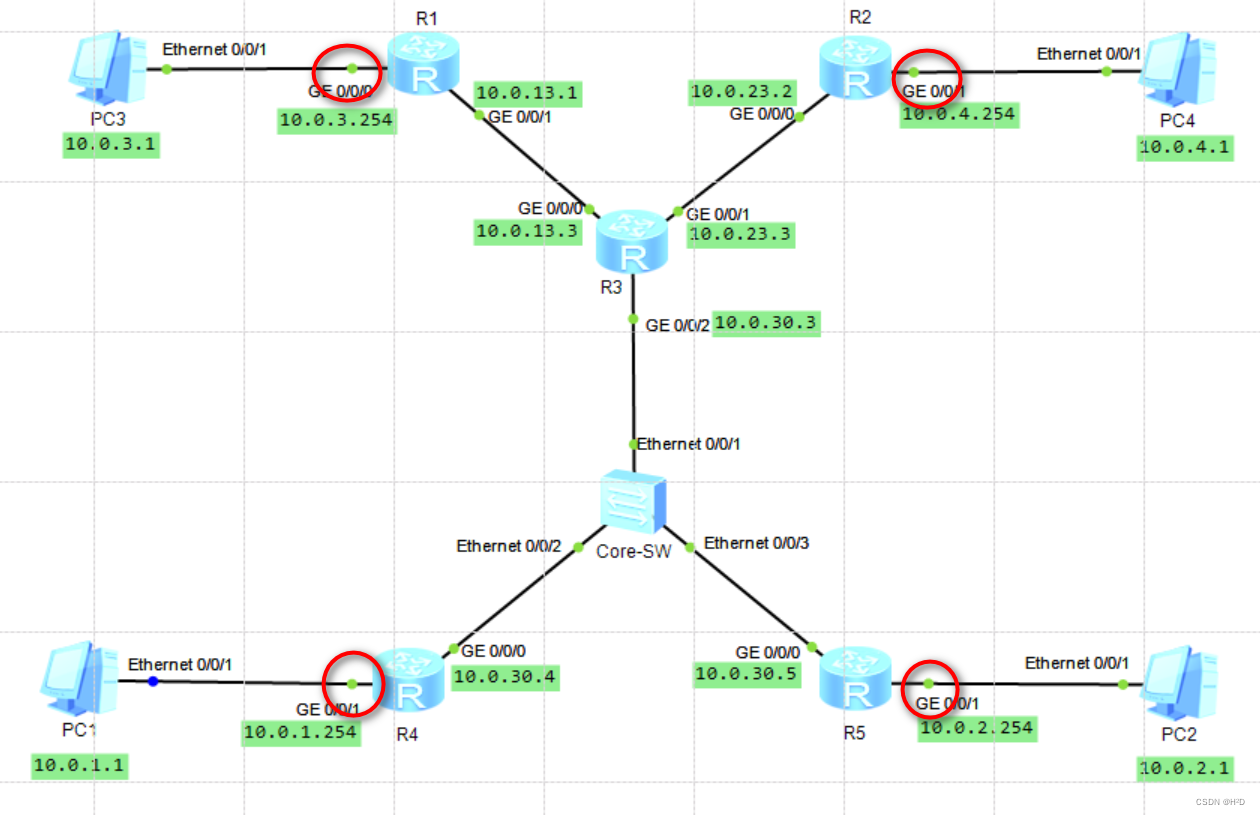
OSPF被动接口配置(华为)
#交换设备 OSPF被动接口配置 一、基本概念 OSPF被动接口,也称为抑制接口,即将路由器某一接口配置为被动接口后,该接口不会再接受和发送OSPF报文 二、使用场景 在路由器与终端相近或者直接相连的一侧配置被动接口 因为OSPF会定期发送报文…...

Android --- 异步操作
同步和异步的差异 同步:在发生某件事后什么也不做,直到该事件完成后,再继续进行 异步:在某件事发生后,可以在等待他完成的时候去处理其他事件,等到该事件发生完成后,再回过头来处理它。 异步…...
MOS管专题--->(10)MOS管的封装)
(55)MOS管专题--->(10)MOS管的封装
(10)MOS管的封装 1 目录 (a)IC简介 (b)数字IC设计流程 (c)Verilog简介 (d)MOS管的封装 (e)结束 1 IC简介 (a)在IC设计中,设计师使用电路设计工具(如EDA软件)来设计和模拟各种电路,例如逻辑电路、模拟电路、数字信号处理电路等。然后,根据设计电路的…...

超高清图像生成新SOTA!清华唐杰教授团队提出Inf-DiT:生成4096图像比UNet节省5倍内存。
清华大学唐杰教授团队最近在生成超高清图像方面的新工作:Inf-DiT,通过提出一种单向块注意力机制,能够在推理过程中自适应调整内存开销并处理全局依赖关系。基于此模块,该模型采用了 DiT 结构进行上采样,并开发了一种能…...
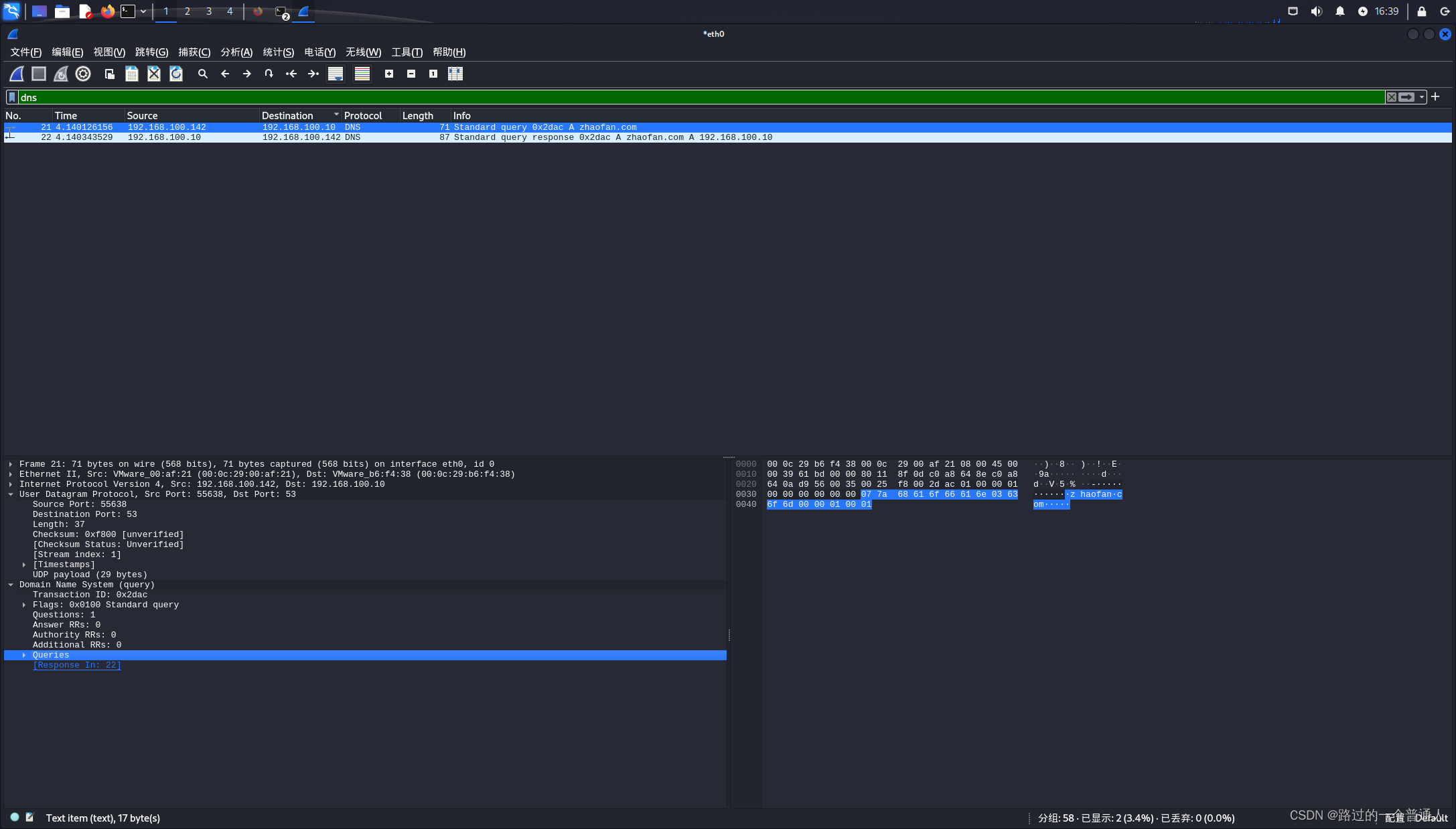
网络安全 - DNS劫持原理 + 实验
DNS 劫持 什么是 DNS 为什么需要 DNS D N S \color{cyan}{DNS} DNS(Domain Name System)即域名系统。我们常说的 DNS 是域名解析协议。 DNS 协议提供域名到 IP 地址之间的解析服务。计算机既可以被赋予 IP 地址,也可以被赋予主机名和域名。用…...
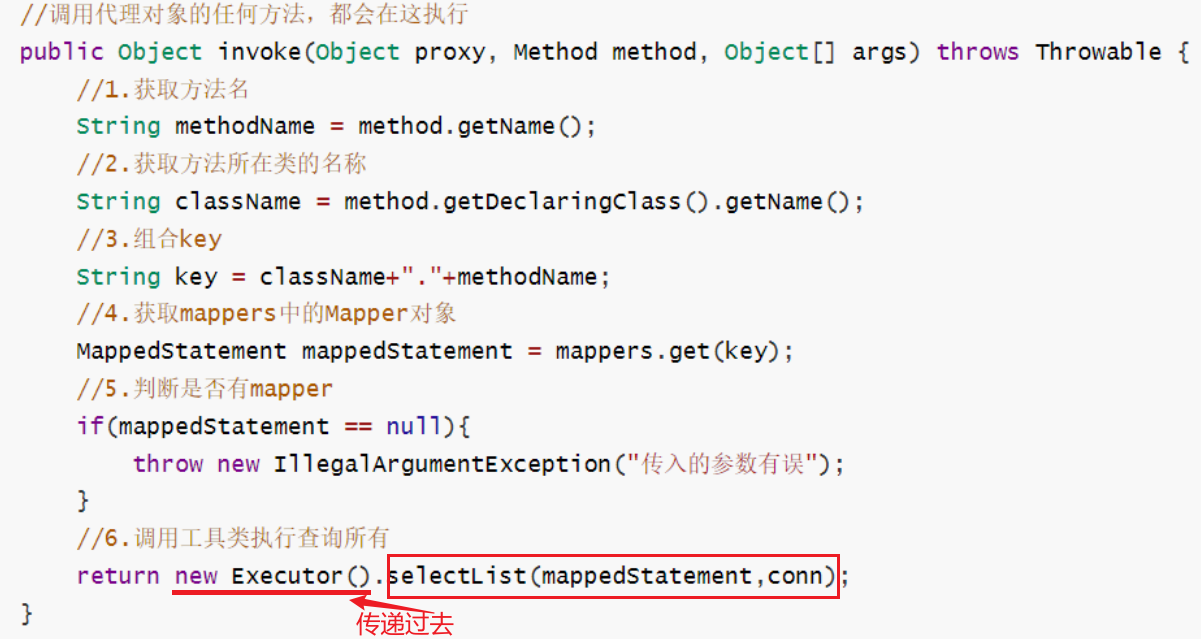
MyBatis的运行原理
目录 1、目的:梳理一下MyBatis运行时的几个对象,我们需要搞清楚他们的作用,进而需要理解mybatis的整个工作流程和执行原理。 2、简要概括各个类 2.1 Resources 作用:编写资源加载类,使用类加载器加载 配置文件(myb…...

算法题解记录29+++全排列(百日筑基)
一、题目描述 题目难度:中等 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示…...

苹果AI功能,AI训练数据缺乏,SD3推出,MJ6推出新特性
更多信息: https://agifun.love 智源社区 2024智源大会议程公开丨大模型前沿探索 2024年6月14日-15日,第6届北京智源大会将以线下与线上结合的形式召开,线下会场设在中关村国家自主创新示范区会议中心。2024智源大会再次以全球视野&#x…...

超越中心化:Web3如何塑造未来数字生态
随着技术的不断发展,人们对于网络和数字生态的期望也在不断提升。传统的中心化互联网模式虽然带来了便利,但也暴露出了诸多问题,比如数据滥用、信息泄露、权力集中等。在这样的背景下,Web3技术应运而生,旨在打破传统中…...
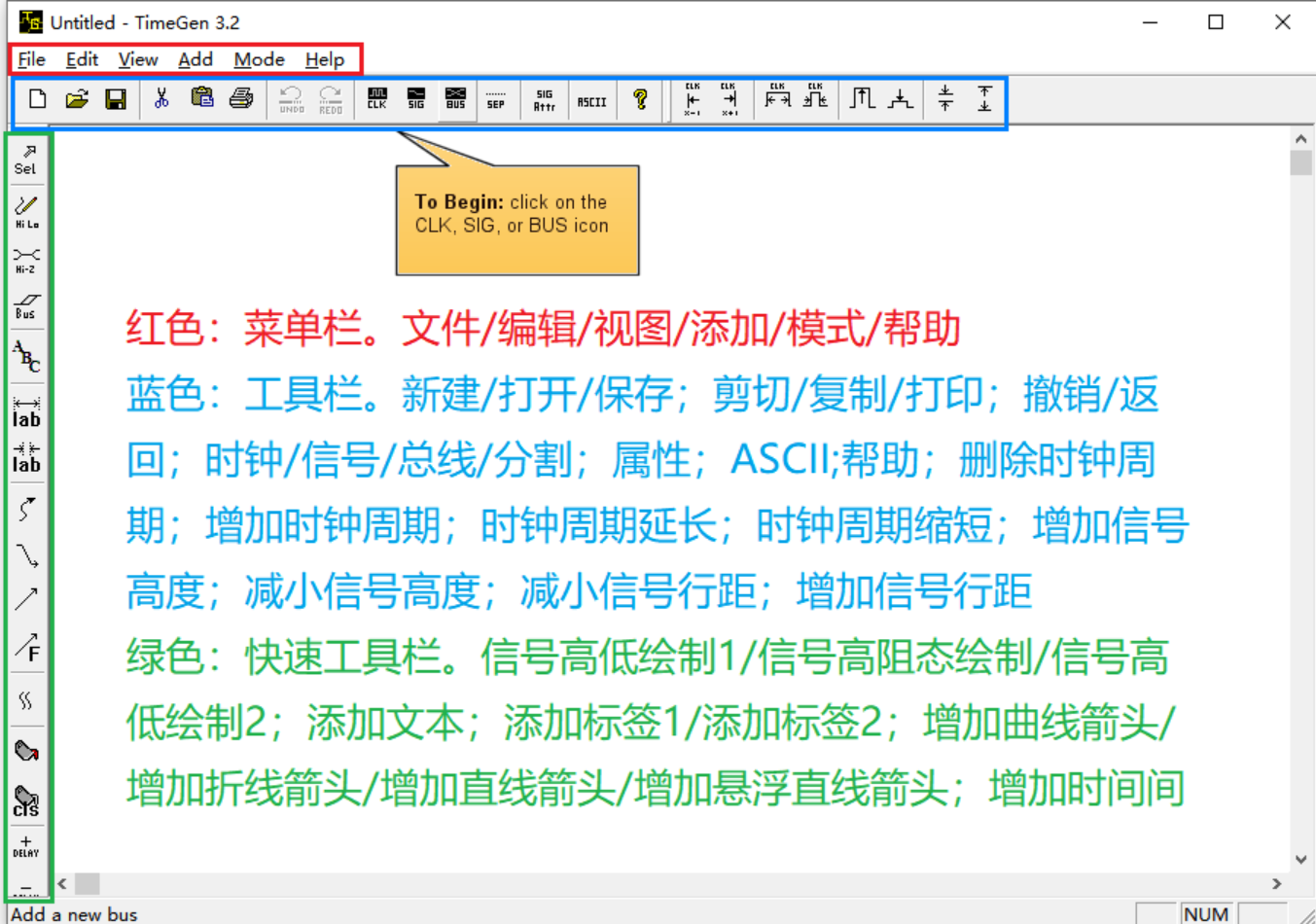
【ic-tool】timegen使用
一、前言 TimeGen是一个用于时序波形编辑的CAD工具,它允许数字设计工程师快速有效地绘制数字时序图。TimeGen时序图可以很容易地导出到其他窗口程序,如microsoftword,用于编写设计规范。可直接从官网下载TimeGEN软件:TimeGen Pro…...
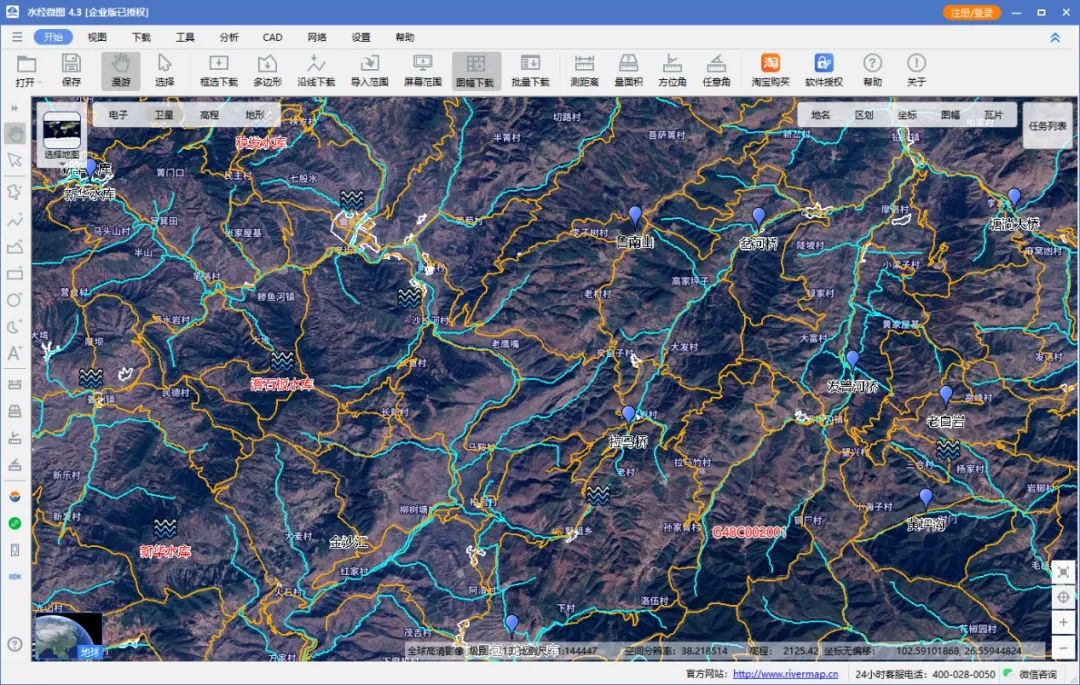
1:25万基础电子地图(云南版)
我们在《50幅1:25万基础电子地图(四川版)》一文中,为你分享过四川的50幅基础电子地图。 现在我们再为你分享云南的1:25万基础电子地图,你可以在文末查看该数据的领取方法。 基础电子地图云南版 下载后可以看到该数据…...
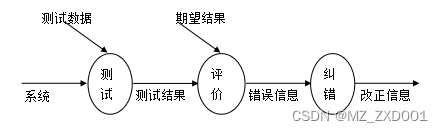
springboot宠物领养系统-计算机毕业设计源码07863
摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存…...

牛客热题:最长回文子串
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:最长回文子串题目链接方法一&am…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
