如果搜索一定超时,如何用dp来以空间换时间
E - Alphabet Tiles (atcoder.jp)
题目大意:1到k长度的字符串时,在A-Z给定数量下,搭配出多少种不同的字符串
思路
排列组合,会死人的
暴搜:可以解决,但是时间太长
dp:考虑前 i 个字母,在长度为 j 下的字符串,有多少种情况,这是一个背包问题
难点
现在难点就来到了转移函数了
首先 i 可以继承 i-1,对于每个字母,遍历它的个数t(1到 l ,其中 l 是当前遍历的长度与字母个数的最小值),把 j-t的方案数乘以C(j,k) [相当于是分步乘法,把没有这个字母下j-t个已排好的位置放入c个当前字母,所以乘以“在j个位置下挑c个位置,用组合数”]
难点二:初始值,把dp[0][0] 和 dp[i][0] 都置为1,情况数为1
#include<bits/stdc++.h>
using namespace std;
#define ll long longll dp[30][1005];
ll C[1005][1005];
const int N = 998244353;int main()
{int k;cin >> k;for(int i = 0 ; i <= k ; i++){C[i][0] = 1;for(int j = 1 ; j <= i ; j++){C[i][j] = C[i-1][j] + C[i-1][j-1];C[i][j] %= N; }}dp[0][0] = 1;for(int i = 1 ; i <= 26 ; i++){int c;cin >> c;dp[i][0] = 1;for(int j = 1 ; j <= k ; j++){for(int l = 0 ; l <= min(j,c) ; l++){dp[i][j] = dp[i][j] + dp[i-1][j-l]*C[j][l]%N; //加上使用字母0次、1次、2次的情况 dp[i][j] %= N; }}}ll ans = 0;for(int i = 1 ; i <= k ; i++){ans += dp[26][i];ans %= N; }cout << ans;return 0;
}反思
转移函数除了考虑从哪里转来,还要考虑自身的结果是怎么计算的(满足题意,不重不漏,用在本题里就是每个长度的串考虑用上0个、1个、2个当前字母),还要考虑自身会被哪些值在遍历时影响到,或有多次赋值,思考如何保证值在被累加或是其它积累。
相关文章:

如果搜索一定超时,如何用dp来以空间换时间
E - Alphabet Tiles (atcoder.jp) 题目大意:1到k长度的字符串时,在A-Z给定数量下,搭配出多少种不同的字符串 思路 排列组合,会死人的 暴搜:可以解决,但是时间太长 dp:考虑前 i 个字母&…...

MySQL常见的命令
MySQL常见的命令 查看数据库(注意添加分号) show databases;进入到某个库 use 库; 例如:进入test use test;显示表格 show tables;直接展示某个库里面的表 show tables from 库; 例如:展示mysql中的表格 show tabl…...

11 类型泛化
11 类型泛化 1、函数模版1.1 前言1.2 函数模版1.3 隐式推断类型实参1.4 函数模板重载1.5 函数模板类型形参的默认类型(C11标准) 2、类模版2.1 类模板的成员函数延迟实例化2.2 类模板的静态成员2.3 类模板的递归实例化2.4 类模板类型形参缺省值 3、类模板…...
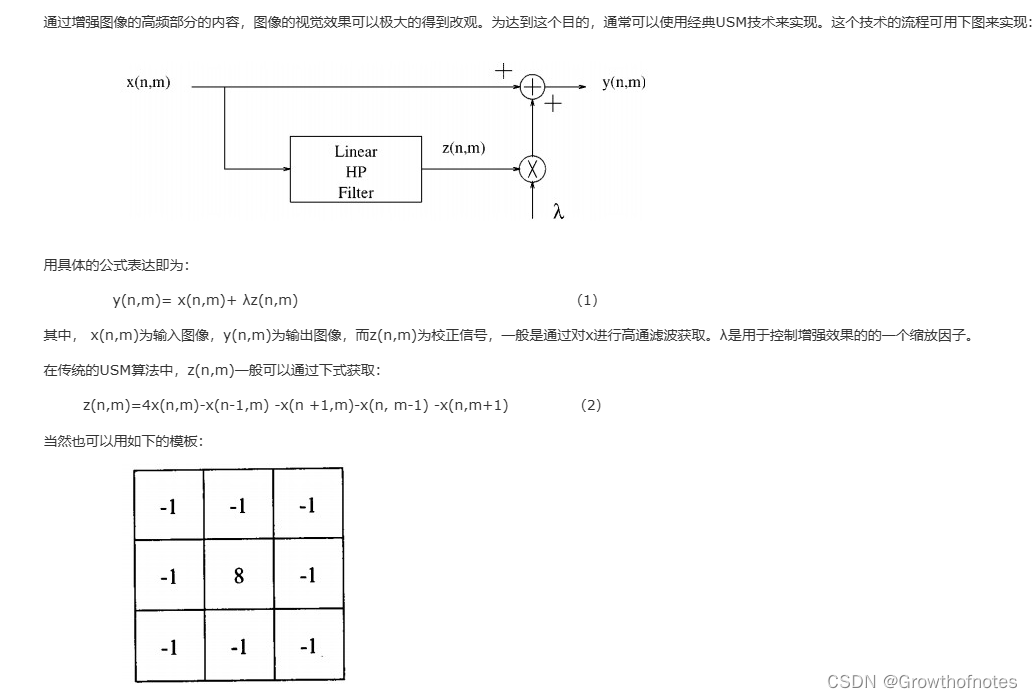
UE4_后期_ben_模糊和锐化滤镜
学习笔记,不喜勿喷,侵权立删,祝愿生活越来越好! 本篇教程主要介绍后期处理的简单模糊和锐化滤镜效果,学习之前首先要回顾下上节课介绍的屏幕扭曲效果: 这是全屏效果,然后又介绍了几种蒙版&#…...

Spring Boot中Excel的导入导出的实现之Apache POI框架使用教程
文章目录 前言一、Apache POI 是什么?二、使用 Apache POI 实现 Excel 的导入和导出① 导入 Excel1. 添加依赖2. 编写导入逻辑3. 在 Controller 中处理上传请求 ② 导出 Excel1. 添加依赖2. 编写导出逻辑3. 在 Controller 中处理导出请求 总结 前言 在 Spring Boot …...

CentOS搭建kubernetes集群详细过程(yum安装方式)
kubernetes集群搭建详细过程(yum安装方式) Kubernetes,也被称为K8s,是一个多功能的容器管理工具,它不仅能够协调和调度容器的部署,而且还能监控容器的健康状况并自动修复常见问题。这个平台是在谷歌十多年…...

Java 面试题:Java 的 Exception 和 Error 有什么区别?
在Java编程中,异常处理是确保程序稳健性和可靠性的重要机制。Java提供了一套完善的异常处理框架,通过捕获和处理异常,开发者可以有效地应对程序运行时可能出现的各种问题。在这一框架中,Exception和Error是两个核心概念࿰…...

在Vue 3中,el-select循环el-option的常见踩坑点,value值绑定对象类型?选中效果不准确?
在Vue 3中,el-select 组件是来自 Element Plus UI 库的一部分。 如果你想要设置默认选中的选项,你可以使用 v-model 来绑定选中的值。如果你想要在某个时刻让某个选项显示为已选中,可以设置对应的值到 v-model 绑定的数据。 <template>…...

Qt实现单例模式:Q_GLOBAL_STATIC和Q_GLOBAL_STATIC_WITH_ARGS
目录 1.引言 2.了解Q_GLOBAL_STATIC 3.了解Q_GLOBAL_STATIC_WITH_ARGS 4.实现原理 4.1.对象的创建 4.2.QGlobalStatic 4.3.宏定义实现 4.4.注意事项 5.总结 1.引言 设计模式之单例模式-CSDN博客 所谓的全局静态对象,大多是在单例类中所见,在之前…...

通过nginx转发后应用偶发502bad gateway
序言 学习了一些东西,如何才是真正自己能用的呢?好像就是看自己的潜意识的反应,例如解决了一个问题,那么下次再碰到类似的问题,能直接下意识的去找到对应的信息,从而解决,而不是和第一次碰到一样…...

linux中如何进行yum源的挂载
linux中如何进行yum源的挂载 1.首先创建目录[rootserver /]# mkdir /rhel92.使用mount命令进行、dev/cdrom/的镜像文件进行挂载[rootserver /]# mount /dev/cdrom /rhel9/ 注意:此时设立的是临时命令。重启后则失效,若想在下次开启后仍然挂载&a…...

ffmpeg的部署踩坑及简单使用方式
ffmpeg的使用方式有以下几种: 使用原生安装包 直接在ffmpeg官网上下载安装该软件,加入到环境变量中就可以使用了 优点:简单,灵活,代码中也不用添加其他第三方的包 缺点:需要手动安装ffmpeg,这点比较麻烦 部署-windows 在windows环境下,有时就算加入到了环境变量,…...
misc刷题记录2[陇剑杯 2021]
[陇剑杯 2021]webshell (1)单位网站被黑客挂马,请您从流量中分析出webshell,进行回答: 黑客登录系统使用的密码是_____________。得到的flag请使用NSSCTF{}格式提交。 这里我的思路是,既然要选择的时间段是黑客登录网站以后&…...

AI发展面临的问题? —— AI对创造的重新定义
一、AI的问题描述 AI与数据安全问题:随着AI技术的发展和应用,数据安全问题日益突出。AI模型训练依赖于大量数据,而这些数据中可能包含个人隐私、商业秘密等敏感信息。如果数据在采集、存储、使用过程中处理不当,可能导致数据泄露或…...
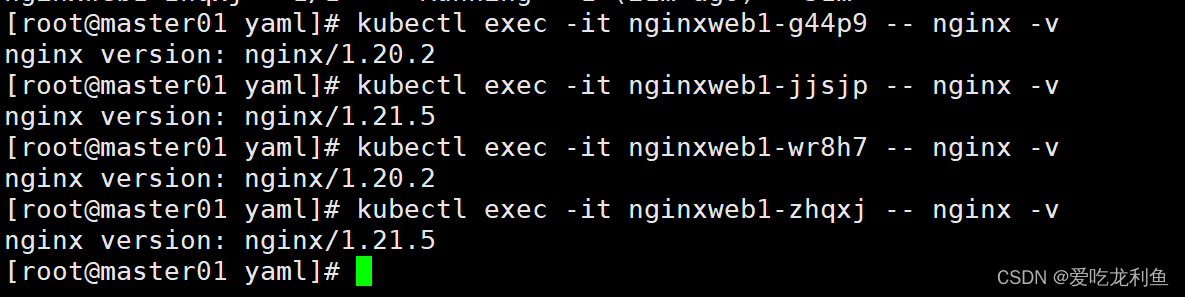
k8s学习--OpenKruise详细解释以及原地升级及全链路灰度发布方案
文章目录 OpenKruise简介OpenKruise来源OpenKruise是什么?核心组件有什么?有什么特性和优势?适用于什么场景? 什么是OpenKruise的原地升级原地升级的关键特性使用原地升级的组件原地升级的工作原理 应用环境一、OpenKruise部署1.安…...
上海亚商投顾:沪指缩量调整 PCB概念股持续爆发
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 大小指数昨日走势分化,沪指全天震荡调整,创业板指午后涨超1%。消费电子板块全天强势&a…...
QT属性系统,简单属性功能快速实现 QT属性的简单理解 属性学习如此简单 一文就能读懂QT属性 QT属性最简单的学习
4.4 属性系统 Qt 元对象系统最主要的功能是实现信号和槽机制,当然也有其他功能,就是支持属性系统。有些高级语言通过编译器的 __property 或者 [property] 等关键字实现属性系统,用于提供对成员变量的访问权限,Qt 则通过自己的元对…...

【IEEE出版丨EI检索】2024新型电力系统与电力电子国际会议(NPSPE 2024)
2024新型电力系统与电力电子国际会议(NPSPE 2024)将于8月16日至18日在中国大连举行,本届大会致力于为相关领域的专家和学者提供一个探讨行业热点问题,促进科技进步,增加科研合作的平台。本届大会涵盖新型电力系统和电力…...
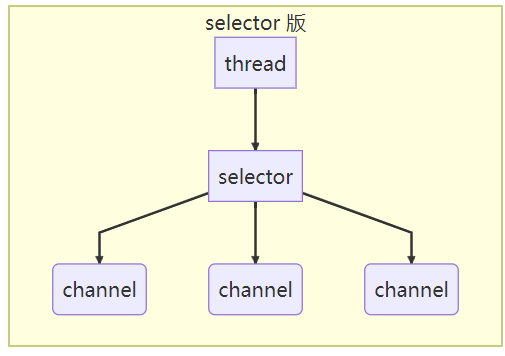
【Netty】nio阻塞非阻塞Selector
阻塞VS非阻塞 阻塞 阻塞模式下,相关方法都会导致线程暂停。 ServerSocketChannel.accept() 会在没有建立连接的时候让线程暂停 SocketChannel.read()会在没有数据的时候让线程暂停。 阻塞的表现就是线程暂停了,暂停期间不会占用CPU,但线程…...

ES 操作
1、删除索引的所有记录 curl -X POST "localhost:9200/<index-name>/_delete_by_query" -H Content-Type: application/json -d {"query": {"match_all": {}} }POST /content_erp_nlp_help/_delete_by_query { "query": { &quo…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
