算法 | 子集数排列树满m叉树二分搜索归并排序快速排序
子集树:O(2^n)
一个序列的所有子集为2^n,即可看成具有2^n个叶节点的满二叉树
int backtrack(int k) //k表示扩展结点在解空间树中所处的层次
{if(k>n) //n标识问题的规模output(x); //x是存放当前解的一维数组if(constraint(k)) //约束函数{ //做相关标识backtrack(k+1)//做相关标识的反操作 } if(bound(k)) //限定函数{//做相关标识backtrack(k+1)//做相关标识的反操作 }}常用于:解空间为子集树的常见问题:
(1)0-1背包问题;
(2)子集和问题;
(3)装载问题;
(4)最大团问题。
排序树:O(n!)
int backtrack(int t) //t表示扩展结点在解空间树中所处的层次
{if(t>n) //n标识问题的规模output(x); //x是存放当前解的一维数组else{for(int i=t;i<=n;i++){swap(x[t],x[i]); //实现两个位置的交换if(constraint(t)&&bound(t)) //约束函数与限定函数backtrack(t+1) //递归swap(x[t],x[i]); //恢复原状}}}
解空间为排列树的常见问题:
(1)n皇后问题;
(2)旅行商问题;
(3)园排列问题;
(4)电路板排列问题。
满m叉树:O(n*m^n)
地图着色问题:
每个元素有M种选择
二分搜索法:最好:O(1) 最坏:O(logn)
二分搜索法(Binary Search)是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。
最好时间复杂度:
在二分搜索法中,如果我们要查找的元素正好是数组的中间元素,那么我们只需要一次比较就能找到它。因此,最好的情况下,二分搜索的时间复杂度是 O(1)。但是,严格来说,我们通常说二分搜索的最好时间复杂度是 O(log n),因为这只是平均情况或最好情况的一种特例,而平均情况或最好情况通常需要 log n 次比较(当 n 是数组的长度时)。最坏时间复杂度:
在二分搜索法中,最坏的情况是我们要查找的元素不在数组中,或者它在数组的最左边或最右边。在这种情况下,我们需要不断地缩小搜索范围,直到搜索范围为空。每次比较,我们都将搜索范围减半,因此,在最坏的情况下,我们需要 log n 次比较(这里 log 是以 2 为底的对数)。所以,二分搜索的最坏时间复杂度是 O(log n)。
归并排序
#include <iostream>
using namespace std;void Merge(int A[], int low, int mid, int high)
{int* B = new int[high - low + 1];int i = low, j = mid + 1, k = 0;while (i <= mid && j <= high){if (A[i] <= A[j])B[k++] = A[i++];elseB[k++] = A[j++];}while (i <= mid) B[k++] = A[i++];while (j <= high) B[k++] = A[j++];// 修正:复制B到A时,确保k从0开始 for (int p = 0; p < k; p++)A[low + p] = B[p]; // 使用low + p来确保复制到正确的位置 delete[] B; // 释放动态分配的内存
}void MergeSort(int A[], int low, int high)
{if (low < high){int mid = (low + high) / 2;// 修正:递归调用应该包括mid MergeSort(A, low, mid);MergeSort(A, mid + 1, high);Merge(A, low, mid, high);}
}int main()
{int a[] = { 1, 2, 54, 25, 76, 23 };int n = sizeof(a) / sizeof(a[0]); // 计算数组长度 MergeSort(a, 0, n - 1); // 修正:传入正确的high值 for (int i = 0; i < n; i++) // 修正:打印所有元素 cout << a[i] << " "; // 添加空格分隔符 cout << endl; // 打印换行符 return 0;
}这三行代码是归并排序(Merge Sort)算法中的关键步骤。归并排序是一种分治(Divide and Conquer)策略的排序算法。
MergeSort(A, low, mid);这行代码是递归地调用归并排序函数本身,用于对数组的左半部分进行排序。这
2.MergeSort(A, mid + 1, high);这行代码与第一行类似,但它是用于对数组的右半部分进行排序。
3.Merge(A, low, mid, high);当左半部分和右半部分都已经被排序后,这行代码用于将这两个已排序的子数组合并成一个已排序的完整数组。
快速排序
void QuickSort(int array[], int low, int high) {int i = low; int j = high;if(i >= j) {return;}int temp = array[low];while(i != j) {while(array[j] >= temp && i < j) {j--;}while(array[i] <= temp && i < j) {i++;}if(i < j) {swap(array[i], array[j]);}}//将基准temp放于自己的位置,(第i个位置)swap(array[low], array[i]);QuickSort(array, low, i - 1);QuickSort(array, i + 1, high);
}相关文章:

算法 | 子集数排列树满m叉树二分搜索归并排序快速排序
子集树:O(2^n) 一个序列的所有子集为2^n,即可看成具有2^n个叶节点的满二叉树 int backtrack(int k) //k表示扩展结点在解空间树中所处的层次 {if(k>n) //n标识问题的规模output(x); //x是存放当前解的一维数组if(constraint(k)…...

SpringBoot配置第三方专业缓存技术jetcache方法缓存方案
jetcache方法缓存 我们可以给每个方法配置缓存方案 JetCache 是一个基于 Java 的缓存库,支持多种缓存方案和缓存策略,主要用于提升应用程序的性能和响应速度。它提供了多种缓存模式和特性,可以根据需求选择合适的缓存方案。 JetCache 的主…...
游戏开发丨基于PyGame的消消乐小游戏
文章目录 写在前面PyGame消消乐注意事项系列文章写在后面 写在前面 本期内容:基于pygame实现喜羊羊与灰太狼版消消乐小游戏 下载地址:https://download.csdn.net/download/m0_68111267/88700193 实验环境 python3.11及以上pycharmpygame 安装pygame…...
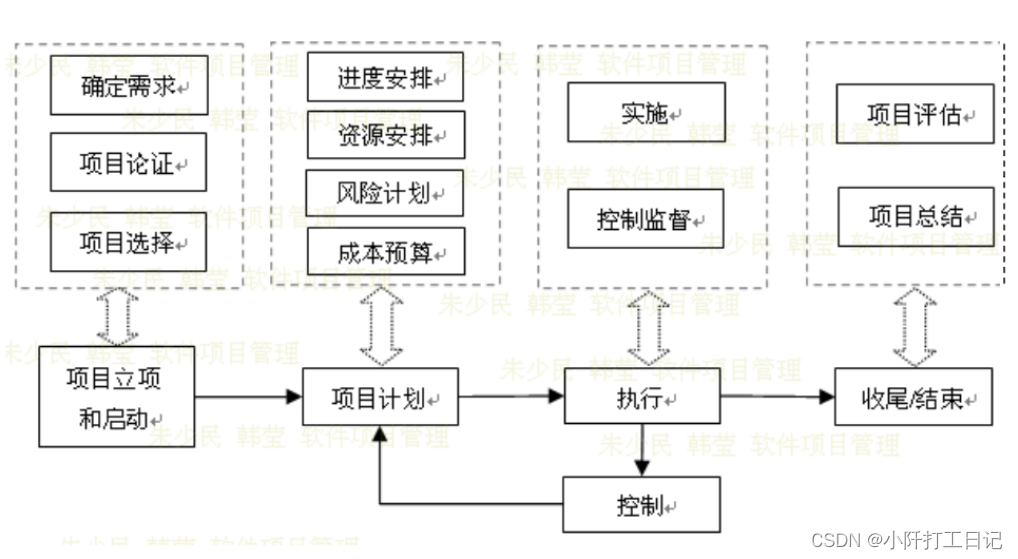
软件项目管理概述
1.什么是项目? 2.项目管理的定义 3.项目管理的本质 4.项目成功的标志 5.项目管理的基本方法 6.项目的生命周期(启动 计划 执行 控制 结束) 7.结合生活中的某件事,谈谈项目管理的作用 项目管理在日常生活中扮演着重要的角色&…...

FastAdmin后台开发框架 lang 任意文件读取漏洞复现
0x01 产品简介 FastAdmin是一款基于PHPBootstrap的开源后台框架,专为开发者精心打造。它基于ThinkPHP和Bootstrap两大主流技术构建,拥有完善的权限管理系统和一键生成CRUD等强大功能。FastAdmin致力于提高开发效率,降低开发成本,…...

数字时代PLM系统的重要性
什么是 PLM(产品生命周期管理)? 从最基本的层面上讲,产品生命周期管理 (PLM)是管理产品从最初构思、开发、服务和处置的整个过程的战略流程。换句话说,PLM 意味着管理产品从诞生到消亡所涉及的一切。 什么是 PLM 软件…...

安卓实现圆形按钮轮廓以及解决无法更改按钮颜色的问题
1.实现按钮轮廓 在drawable文件新建xml文件 <shape xmlns:android"http://schemas.android.com/apk/res/android"<!--实现圆形-->android:shape"oval"><!--指定内部的填充色--><solid android:color"#FFFFFF"/><!-…...

常用原语介绍
1.在Xilinx的example(wavegen example)中看到他们的顶层模块的输入输出管脚都手动例化原语IBUF以及OBUF——工具也会自动给我们加上不必要自己加 2.非mrcc个srcc的管脚输入的时钟信号,无法进入mmcm和bufg————试验过会报错 3.实际上&…...
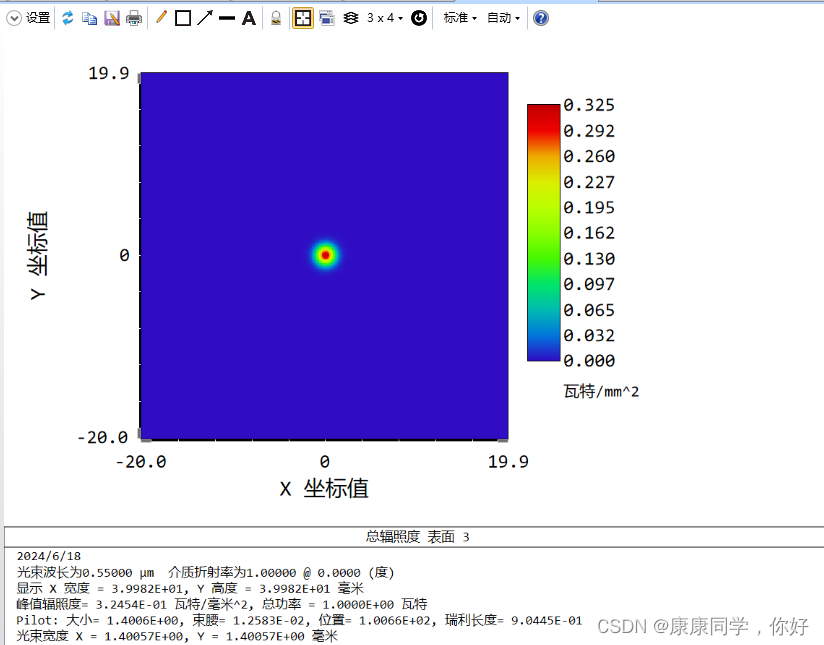
29. 透镜阵列
导论: 物理传播光学(POP)不仅可以用于简单系统,也可以设计优化复杂的光学系统,比如透镜阵列。 设计流程: 透镜阵列建模 在孔径类型中选择“入瞳直径”,并输入2 在视场设定中。设置一个视场&…...

深入理解并打败C语言难关之一————指针(3)
前言: 昨天把指针最为基础的内容讲完了,并且详细说明了传值调用和传址调用的区别(这次我也是做到了每日一更,感觉有好多想写的但是没有写完),下面不多废话,下面进入本文想要说的内容 目录&#…...
Ubuntu-24.04-live-server-amd64启用ssh
系列文章目录 Ubuntu-24.04-live-server-amd64安装界面中文版 Ubuntu安装qemu-guest-agent Ubuntu乌班图安装VIM文本编辑器工具 文章目录 系列文章目录前言一、输入安装命令二、使用私钥登录(可选)1.创建私钥2.生成三个文件说明3.将公钥复制到服务器 三…...
)
Leetcode 2786. 访问数组中的位置使分数最大(DP 优化)
Leetcode 2786. 访问数组中的位置使分数最大 DP 以每个位置为结尾的序列的分数取决于前方的分数,根据奇偶性计算,取最大值 超时 class Solution {public long maxScore(int[] nums, int x) {int n nums.length;long dp[] new long[n];Arrays.fill(dp…...

【docker实战】使用Dockerfile的COPY拷贝资源遇到的问题
事情是这样的。 在我负责的golang项目中,使用硬代码验证某块逻辑。比如: 于是,为了解决硬代码的问题,我制作了表格工具:【开源项目】Excel数据表自动生成工具v1.0版 – 经云的清净小站 (skycreator.top)。 使用表格工…...

如何用多线程执行 unittest 测试用例实现方案
前言 使用python做过自动化测试的小伙伴,想必都知道unittest和pytest这两个单元测试框架,其中unittest是python的官方库,功能相对于pytest来要逊色不少,但是uniitest使用上手简单,也受到的很多的小伙伴喜爱。一直以来都…...

Ascend310 EP模式下容器内进行推理测试
EP模式下容器内进行推理测试 本文的软硬件环境如下: 机器:x86台式机一台 OS: 5.4.0-26-generic Ubuntu20.04 LTS 推理卡:DLAP200-HP-2(凌华基于atlas200模块打造的两模块推理卡) 1. 推理卡固件和驱动安…...
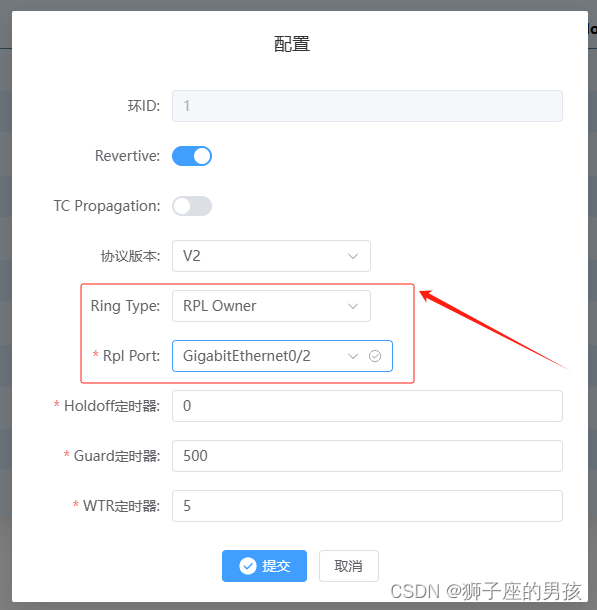
(el-Transfer)操作(不使用 ts):Element-plus 中 Select 组件动态设置 options 值需求的解决过程
Ⅰ、Element-plus 提供的Select选择器组件与想要目标情况的对比: 1、Element-plus 提供Select组件情况: 其一、Element-ui 自提供的Select代码情况为(示例的代码): // Element-plus 提供的组件代码: <template><div class"f…...

Java基础之Math与Array类与System
文章目录 一、Math.random()二、Arrays.binarySearch()三、asList()四、System tip:以下是正文部分 一、Math.random() a < num < b int num (int)(Math.random() * (b - a 1)) a二、…...
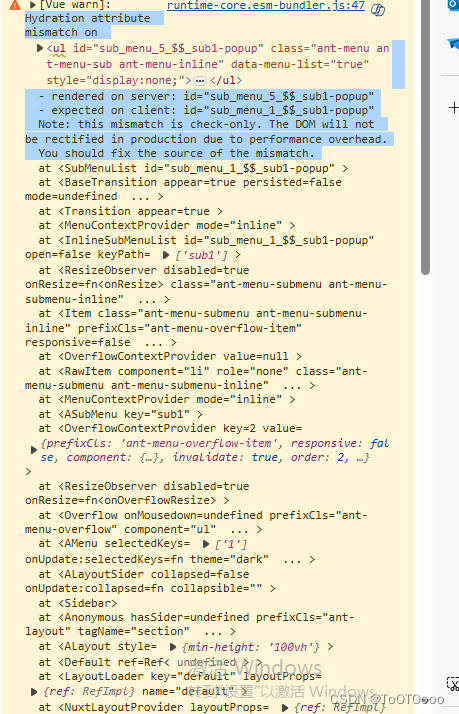
警告:Hydration attribute mismatch on Note: this mismatch is check-only.(水合不匹配)
vue3Nuxt3运行代码是提示如下警告 [Vue warn]: Hydration attribute mismatch on <ul id"sub_menu_5_$$_sub1-popup" class"ant-menu ant-menu-sub ant-menu-inline" data-menu-list"true" style"display:none;">…...

【机器学习】CART决策树算法的核心思想及其大数据时代银行贷款参考案例——机器认知外界的重要算法
目录 引言 概述 CART决策树的特点 核心思想 减少不确定性的指标 基尼系数(Gini Index) 分类错误率 熵 银行实例 背景 数据准备 模型构建 模型评估与优化 应用与结果 代码示例 ✈✈✈✈引言✈✈✈✈ CART算法既可以用于分类问题࿰…...

编程软件是由什么编程的
编程软件是由什么编程的 在数字化的世界里,编程软件作为构建数字生态的基石,其背后所蕴含的奥秘往往令人感到困惑。那么,这些编程软件究竟是由什么编程的呢?这背后隐藏着怎样的逻辑与技术?接下来,我们将从…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

职坐标物联网全栈开发全流程解析
物联网全栈开发涵盖从物理设备到上层应用的完整技术链路,其核心流程可归纳为四大模块:感知层数据采集、网络层协议交互、平台层资源管理及应用层功能实现。每个模块的技术选型与实现方式直接影响系统性能与扩展性,例如传感器选型需平衡精度与…...

初级程序员入门指南
初级程序员入门指南 在数字化浪潮中,编程已然成为极具价值的技能。对于渴望踏入程序员行列的新手而言,明晰入门路径与必备知识是开启征程的关键。本文将为初级程序员提供全面的入门指引。 一、明确学习方向 (一)编程语言抉择 编…...
和向下转型(Downcasting))
【Java基础】向上转型(Upcasting)和向下转型(Downcasting)
在面向对象编程中,转型(Casting) 是指改变对象的引用类型,主要涉及 继承关系 和 多态。 向上转型(Upcasting) ⬆️ 定义 将 子类对象 赋值给 父类引用(自动完成,无需强制转换&…...
