gcn+tcn+transformer入侵检测
gcn
gcn_out = self.gcn(A_hat, D_hat, X) 的公式实际上是图卷积网络(GCN)层的核心操作。具体来说,这一步的计算基于图卷积的基本公式:
H ( l + 1 ) = σ ( D ^ − 1 / 2 A ^ D ^ − 1 / 2 H ( l ) W ( l ) ) H^{(l+1)} = \sigma\left( \hat{D}^{-1/2} \hat{A} \hat{D}^{-1/2} H^{(l)} W^{(l)} \right) H(l+1)=σ(D^−1/2A^D^−1/2H(l)W(l))
在这个公式中:
- H ( l ) H^{(l)} H(l) 是第 l l l 层的节点特征矩阵, H ( 0 ) = X H^{(0)} = X H(0)=X 即输入的节点特征矩阵。
- A ^ \hat{A} A^ 是加入自环后的图的邻接矩阵。
- D ^ \hat{D} D^ 是 A ^ \hat{A} A^ 的度矩阵。
- W ( l ) W^{(l)} W(l) 是第 l l l 层的权重矩阵。
- σ \sigma σ 是激活函数(例如ReLU)。
GCN的公式推导
我们可以具体推导出计算步骤:
-
邻接矩阵和度矩阵:假设图的邻接矩阵为 A A A,我们首先加入自环得到 A ^ = A + I \hat{A} = A + I A^=A+I,其中 I I I 是单位矩阵。然后计算 A ^ \hat{A} A^ 的度矩阵 D ^ \hat{D} D^,其对角线元素为 D ^ i i = ∑ j A ^ i j \hat{D}_{ii} = \sum_j \hat{A}_{ij} D^ii=∑jA^ij。
-
归一化的邻接矩阵:接下来计算 D ^ − 1 / 2 A ^ D ^ − 1 / 2 \hat{D}^{-1/2} \hat{A} \hat{D}^{-1/2} D^−1/2A^D^−1/2,用于对邻接矩阵进行归一化,使得卷积操作不会改变特征的尺度。
-
图卷积操作:最后,将归一化后的邻接矩阵与输入特征矩阵相乘,再与权重矩阵 W W W 相乘,并通过激活函数 σ \sigma σ 得到输出特征矩阵 H ( l + 1 ) H^{(l+1)} H(l+1)。
tcn
在Temporal Convolutional Network(TCN)中,关键操作包括卷积操作、激活函数、丢弃和跳跃连接。以下是TCN中TemporalBlock的推理公式:
- 卷积操作:使用扩展卷积对输入进行时间卷积。
y ( 1 ) = ReLU ( Dropout ( Chomp ( Conv1d ( x , W 1 ) ) ) ) y^{(1)} = \text{ReLU}(\text{Dropout}(\text{Chomp}(\text{Conv1d}(x, W_1)))) y(1)=ReLU(Dropout(Chomp(Conv1d(x,W1))))
- 第二次卷积操作:再次使用扩展卷积,并应用相同的操作。
y ( 2 ) = ReLU ( Dropout ( Chomp ( Conv1d ( y ( 1 ) , W 2 ) ) ) ) y^{(2)} = \text{ReLU}(\text{Dropout}(\text{Chomp}(\text{Conv1d}(y^{(1)}, W_2)))) y(2)=ReLU(Dropout(Chomp(Conv1d(y(1),W2))))
- 跳跃连接:如果输入和输出的维度不同,则使用 1 × 1 1 \times 1 1×1 卷积对输入进行下采样。
res = { x , if n inputs = n outputs Conv1d ( x , W downsample ) , otherwise \text{res} = \begin{cases} x, & \text{if } n_{\text{inputs}} = n_{\text{outputs}} \\ \text{Conv1d}(x, W_{\text{downsample}}), & \text{otherwise} \end{cases} res={x,Conv1d(x,Wdownsample),if ninputs=noutputsotherwise
- 输出计算:将卷积操作后的输出与跳跃连接的结果相加,并通过ReLU激活函数。
output = ReLU ( y ( 2 ) + res ) \text{output} = \text{ReLU}(y^{(2)} + \text{res}) output=ReLU(y(2)+res)
总结起来,TemporalBlock的推理公式如下:
output = ReLU ( Conv1d ( ReLU ( Dropout ( Chomp ( Conv1d ( x , W 1 ) ) ) ) , W 2 ) + res ) \text{output} = \text{ReLU}(\text{Conv1d}(\text{ReLU}(\text{Dropout}(\text{Chomp}(\text{Conv1d}(x, W_1)))), W_2) + \text{res}) output=ReLU(Conv1d(ReLU(Dropout(Chomp(Conv1d(x,W1)))),W2)+res)
其中:
- Conv1d ( x , W ) \text{Conv1d}(x, W) Conv1d(x,W) 表示对输入 x x x 进行卷积操作,卷积核权重为 W W W。
- Chomp \text{Chomp} Chomp 用于去除卷积后多余的填充部分。
- Dropout \text{Dropout} Dropout 是丢弃层,用于防止过拟合。
- ReLU \text{ReLU} ReLU 是激活函数。
- res \text{res} res 是跳跃连接的结果。
transformer
在TransformerBlock中,关键操作包括多头自注意力机制、前馈神经网络层、层归一化和跳跃连接。以下是TransformerBlock的推理公式:
- 多头自注意力机制:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) V Attention(Q,K,V)=softmax(dkQKT)V
其中, Q = K = V = x Q = K = V = x Q=K=V=x, d k d_k dk 是键的维度。多头自注意力输出为:
attn_output = MultiHeadAttention ( x , x , x ) \text{attn\_output} = \text{MultiHeadAttention}(x, x, x) attn_output=MultiHeadAttention(x,x,x)
- 第一跳跃连接和层归一化:
x 1 = LayerNorm ( x + Dropout ( attn_output ) ) x_1 = \text{LayerNorm}(x + \text{Dropout}(\text{attn\_output})) x1=LayerNorm(x+Dropout(attn_output))
- 前馈神经网络层:
ff_output = Linear 2 ( Dropout ( ReLU ( Linear 1 ( x 1 ) ) ) ) \text{ff\_output} = \text{Linear}_2(\text{Dropout}(\text{ReLU}(\text{Linear}_1(x_1)))) ff_output=Linear2(Dropout(ReLU(Linear1(x1))))
- 第二跳跃连接和层归一化:
output = LayerNorm ( x 1 + Dropout ( ff_output ) ) \text{output} = \text{LayerNorm}(x_1 + \text{Dropout}(\text{ff\_output})) output=LayerNorm(x1+Dropout(ff_output))
总结起来,TransformerBlock的推理公式如下:
- 多头自注意力机制:
attn_output = MultiHeadAttention ( x , x , x ) \text{attn\_output} = \text{MultiHeadAttention}(x, x, x) attn_output=MultiHeadAttention(x,x,x)
- 第一跳跃连接和层归一化:
x 1 = LayerNorm ( x + Dropout ( attn_output ) ) x_1 = \text{LayerNorm}(x + \text{Dropout}(\text{attn\_output})) x1=LayerNorm(x+Dropout(attn_output))
- 前馈神经网络层:
ff_output = Linear 2 ( Dropout ( ReLU ( Linear 1 ( x 1 ) ) ) ) \text{ff\_output} = \text{Linear}_2(\text{Dropout}(\text{ReLU}(\text{Linear}_1(x_1)))) ff_output=Linear2(Dropout(ReLU(Linear1(x1))))
- 第二跳跃连接和层归一化:
output = LayerNorm ( x 1 + Dropout ( ff_output ) ) \text{output} = \text{LayerNorm}(x_1 + \text{Dropout}(\text{ff\_output})) output=LayerNorm(x1+Dropout(ff_output))
相关文章:

gcn+tcn+transformer入侵检测
gcn gcn_out self.gcn(A_hat, D_hat, X) 的公式实际上是图卷积网络(GCN)层的核心操作。具体来说,这一步的计算基于图卷积的基本公式: H ( l 1 ) σ ( D ^ − 1 / 2 A ^ D ^ − 1 / 2 H ( l ) W ( l ) ) H^{(l1)} \sigma\left…...

【Python】 了解二分类:机器学习中的基础任务
我已经从你的 全世界路过 像一颗流星 划过命运 的天空 很多话忍住了 不能说出口 珍藏在 我的心中 只留下一些回忆 🎵 牛奶咖啡《从你的全世界路过》 在机器学习和数据科学领域,分类问题是最常见的任务之一。分类问题可以分为多类分…...

搭建PHP开发环境:Linux篇
目录 一、引言 二、环境准备 三、安装Web服务器(Apache) Ubuntu/Debian系统: CentOS/Red Hat系统: 四、安装PHP解释器 Ubuntu/Debian系统: CentOS/Red Hat系统: 五、配置Apache以支持PHP Ubuntu/…...
ROS 自动驾驶多点巡航
ROS 自动驾驶多点巡航: 1、首先创建工作空间: 基于我们的artca_ws; 2、创建功能包: 进入src目录,输入命令: catkin_create_pkg point_pkg std_msgs rospy roscpptest_pkg 为功能包名,后面两个是依赖&a…...
SQL学习,大厂面试真题(1):观看各个视频的平均完播率
各个视频的平均完播率 1、视频信息表 IDAuthorNameCategoryAgeStart Time1张三影视302024-01-01 7:00:002李四美食602024-01-01 7:00:003王麻子旅游902024-01-01 7:00:00 (video_id-视频ID, AuthorName-创作者, tag-类别标签, duration-视频时长(秒&…...
)
2023年全国大学生数学建模竞赛C题蔬菜类商品的自动定价与补货决策(含word论文和源代码资源)
文章目录 一、题目二、word版实验报告和源代码(两种获取方式) 一、题目 2023高教社杯全国大学生数学建模竞赛题目 C题 蔬菜类商品的自动定价与补货决策 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而…...
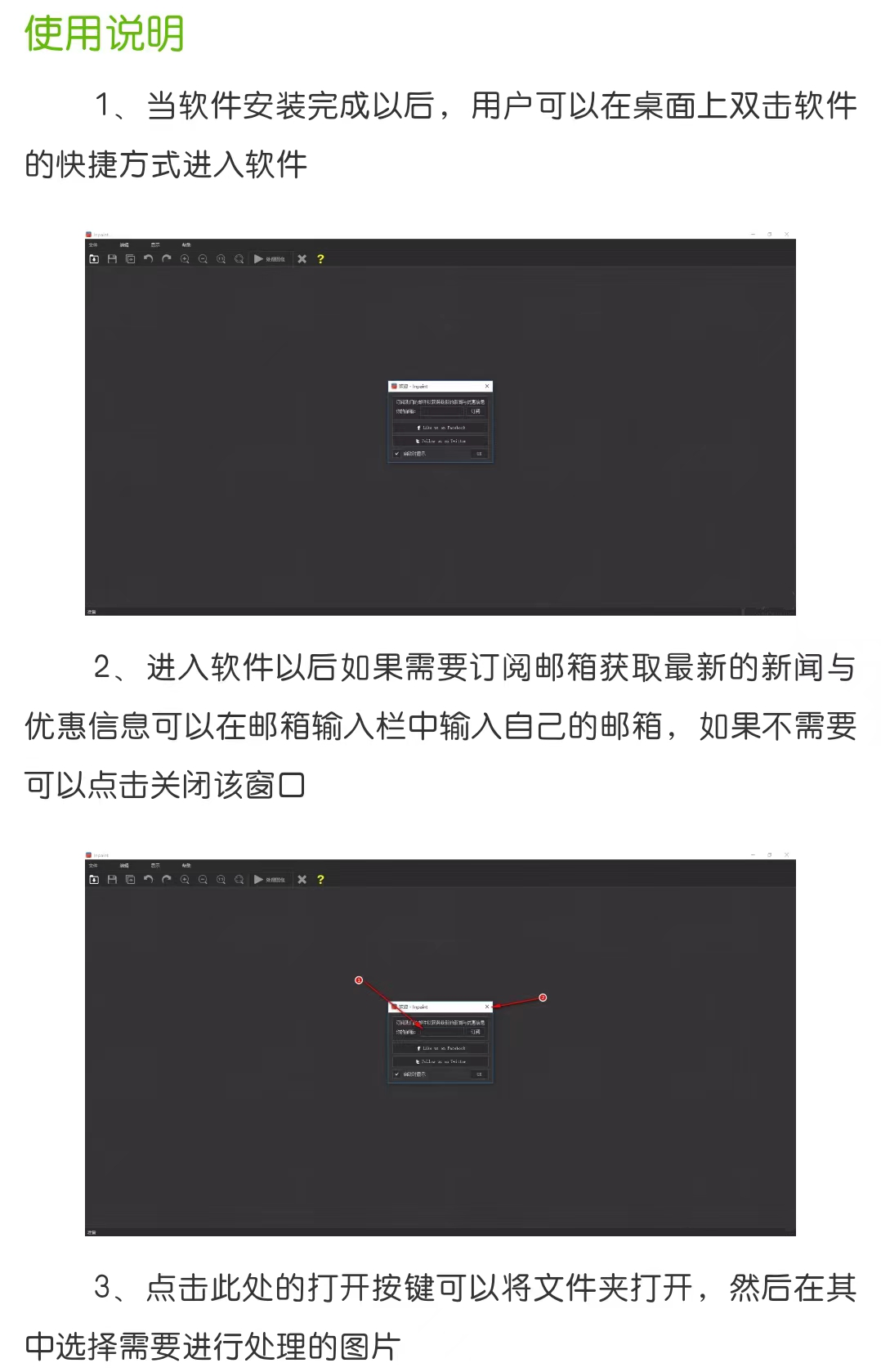
inpaint下载安装2024-inpaint软件安装包下载v5.0.6官网最新版附加详细安装步骤
Inpaint软件最新版是一款功能强大的图片去水印软件,这款软件拥有强大的智能算法,能够根据照片的背景为用户去除照片中的各种水印,并修补好去除水印后的图片。并且软件操作简单、界面清爽,即使是修图新手也能够轻松上手,…...

分享三个仓库
Hello , 我是恒。大概有半个月没有发文章了,都写在文档里了 今天分享三个我开源的项目,比较小巧但是有用 主页 文档导航 Github地址: https://github.com/lmliheng/document 在线访问:http://document.liheng.work/ 里面有各种作者书写的文档ÿ…...

MacOS - 启动台多了个『卸载 Adobe Photoshop』
问题描述 今天安装好了 Adobe Ps,但是发现启动台多了个『卸载 Adobe Photoshop』强迫症又犯了,想把它干掉! 解决方案 打开访达 - 前往 - 资源库,搜索要卸载的名字就可以看到,然后移除到垃圾筐...

PHP 日期处理完全指南
PHP 日期处理完全指南 引言 在PHP开发中,日期和时间处理是一个常见且重要的任务。PHP提供了丰富的内置函数来处理日期和时间,包括日期的格式化、计算、解析等。本文将详细介绍PHP中日期处理的相关知识,帮助读者全面理解和掌握这一技能。 1. PHP日期函数基础 1.1 date()函…...

KVB:怎么样选择最优交易周期?
摘要 在金融交易中,周期的选择是影响交易成败的重要因素之一。不同的交易周期对应不同的市场环境和交易策略,选择合适的周期可以提高交易的成功率。本文将详细探讨交易中如何选择最优周期,包括短周期、中周期和长周期的特点及适用情况&#…...

前端面试题日常练-day69 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末 TypeScript中,以下哪个关键字用于声明一个变量的类型为联合类型? a) union b) any c) all d) | 在TypeScript中,以下哪个符号用于声明一个变量的类型为对象类型&am…...

Java 解析xml文件-工具类
Java 解析xml文件-工具类 简述 Java解析xml文件,对应的Javabean是根据xml中的节点来创建,如SeexmlZbomord、SeexmlIdoc等等 工具类代码 import cn.hutool.core.io.FileUtil; import com.alibaba.cloud.commons.io.IOUtils; import com.seexml.bom.Se…...
PyQt5学习系列之新项目创建并使用widget
PyQt5学习系列之新项目创建并使用widget 前言报错新建项目程序完整程序总结 前言 新建项目,再使用ui转py,无论怎么样都打不开py文件,直接报错。 报错 Connected to pydev debugger (build 233.11799.298)新建项目程序 # Press ShiftF10 to…...
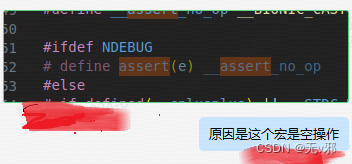
mtk8675 安卓端assert函数的坑
8675 安卓端, assert(pthread_mutex_init(&mutex_data_, &mattr) 0);用这行代码发现pthread_mutex_init函数没有被调用,反汇编发现不光没调用assert,pthread_mutex_init也没调用。直接pthread_mutex_init(&mutex_data_, &ma…...

编程入门笔记:从基础到进阶的探索之旅
编程入门笔记:从基础到进阶的探索之旅 编程,作为现代科技的基石,正日益渗透到我们生活的方方面面。对于初学者来说,掌握编程技能不仅有助于提升解决问题的能力,还能开启通往创新世界的大门。本篇文章将从四个方面、五…...

小规模自建 Elasticsearch 的部署及优化
本文将详细介绍如何在 CentOS 7 操作系统上部署并优化 Elasticsearch 5.3.0,以承载千万级后端服务的数据采集。要使用Elasticsearch至少需要三台独立的服务器,本文所用服务器配置为4核8G的ECS云服务器,其中一台作为 master + data 节点、一台作为 client + data 节点、最后一…...
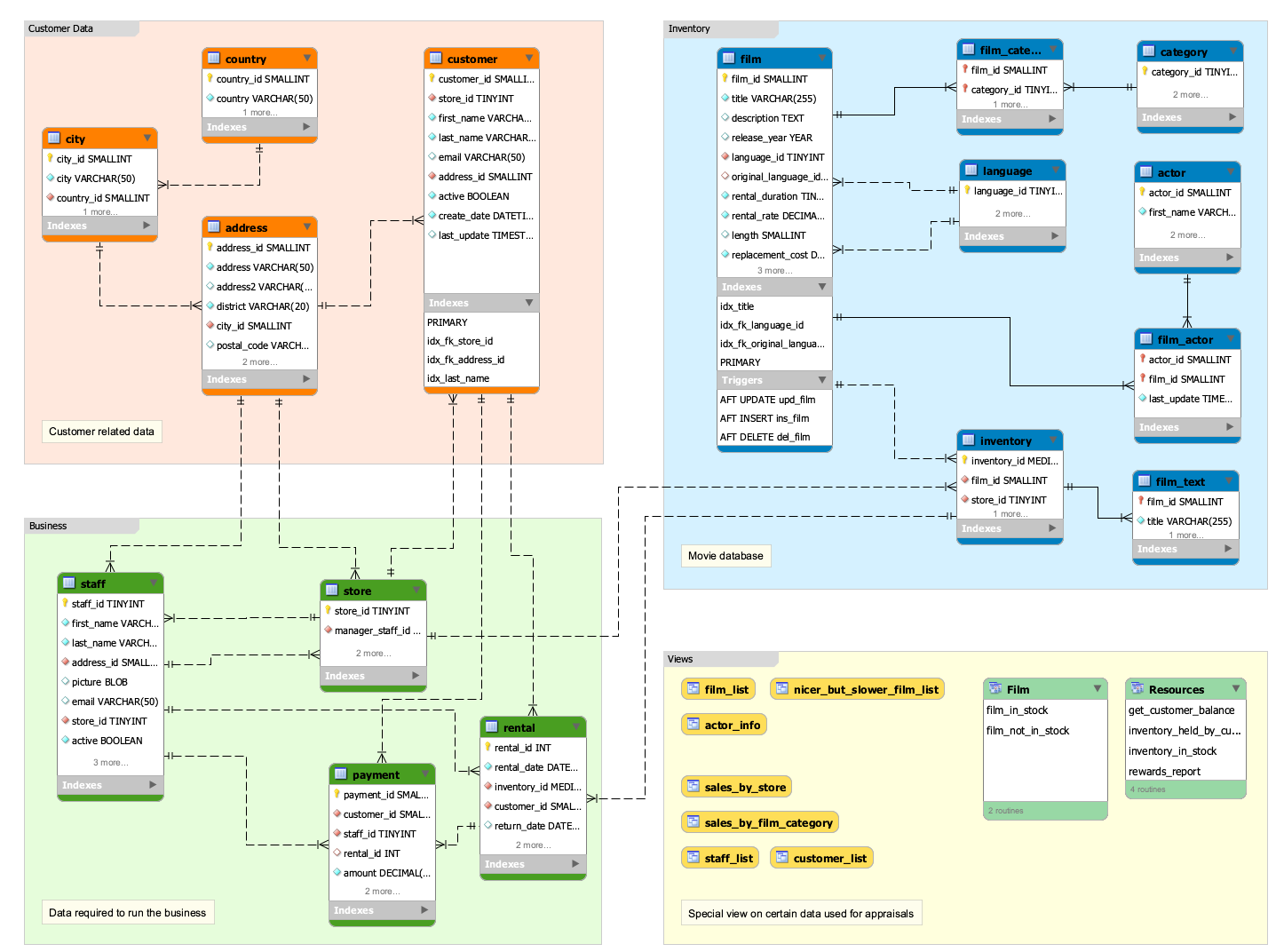
MySQL 示例数据库大全
前言: 我们练习 SQL 时,总会自己创造一些测试数据或者网上找些案例来学习,其实 MySQL 官方提供了好几个示例数据库,在 MySQL 的学习、开发和实践中具有非常重要的作用,能够帮助初学者更好地理解和应用 MySQL 的各种功…...
VirtualBox、Centos7下安装docker后pull镜像问题、ftp上传文件问题
Docker安装篇(CentOS7安装)_docker 安装 centos7-CSDN博客 首先,安装docker可以根据这篇文章进行安装,安装完之后,我们就需要去通过docker拉取相关的服务镜像,然后安装相应的服务容器,比如我们通过docker来安装mysql,…...

链表 题目汇总
237. 删除链表中的节点...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
