Python热涨落流体力学求解算法和英伟达人工智能核评估模型
🎯要点
🎯平流扩散简单离散微分算子 | 🎯相场模拟:简单旋节线分解、枝晶凝固的 | 🎯求解二维波动方程,离散化时间导数
🎯英伟达 A100 人工智能核性能评估模型 | 🎯热涨落流体动力学求解及算法
📜有限差分法 | 本文 - 用例
📜Python和Julia河流湖泊沿海水域特征数值算法模型
📜Python和C++数学物理计算分形热力学静电学和波动方程
📜Python物理学有限差分微分求解器和动画波形传播
📜Python数值和符号算法计算及3D视图物理数学波形方程
📜Python氮氧甲烷乙烷乙烯丙烯气体和固体热力学模型计算
📜Python射频电磁肿瘤热疗数学模型和电磁爆炸性变化统计推理模型

🍇Python有限差分逼近余弦导数
函数 f ( x ) f(x) f(x)在 x = a x=a x=a点的导数 f ′ ( x ) f^{\prime}(x) f′(x)定义为:
f ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a f^{\prime}(a)=\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a} f′(a)=x→alimx−af(x)−f(a)
x = a x=a x=a 处的导数就是此时的斜率。在该斜率的有限差分近似中,我们可以使用点 x = a x=a x=a 附近的函数值来实现目标。不同的应用中使用了多种有限差分公式,下面介绍其中的三种,其中导数是使用两点的值计算的。
前向差分是使用连接 ( x j , f ( x j ) ) \left(x_j, f\left(x_j\right)\right) (xj,f(xj)) 和 ( x j + 1 , f ( x j + 1 ) ) \left(x_{j+1}, f\left(x_{j+1}\right)\right) (xj+1,f(xj+1))的线来估计 x j x_j xj 处函数的斜率:
f ′ ( x j ) = f ( x j + 1 ) − f ( x j ) x j + 1 − x j f^{\prime}\left(x_j\right)=\frac{f\left(x_{j+1}\right)-f\left(x_j\right)}{x_{j+1}-x_j} f′(xj)=xj+1−xjf(xj+1)−f(xj)
后向差分是使用连接 ( x j − 1 , f ( x j − 1 ) ) \left(x_{j-1}, f\left(x_{j-1}\right)\right) (xj−1,f(xj−1)) 和 ( x j , f ( x j ) ) \left(x_j, f\left(x_j\right)\right) (xj,f(xj)) 的线来估计 x j x_j xj 处函数的斜率:
f ′ ( x j ) = f ( x j ) − f ( x j − 1 ) x j − x j − 1 f^{\prime}\left(x_j\right)=\frac{f\left(x_j\right)-f\left(x_{j-1}\right)}{x_j-x_{j-1}} f′(xj)=xj−xj−1f(xj)−f(xj−1)
中间差分是使用连接 ( x j − 1 , f ( x j − 1 ) ) \left(x_{j-1}, f\left(x_{j-1}\right)\right) (xj−1,f(xj−1)) 和 ( x j + 1 , f ( x j + 1 ) ) \left(x_{j+1}, f\left(x_{j+1}\right)\right) (xj+1,f(xj+1)) 的线来估计 x j x_j xj 处函数的斜率:
f ′ ( x j ) = f ( x j + 1 ) − f ( x j − 1 ) x j + 1 − x j − 1 f^{\prime}\left(x_j\right)=\frac{f\left(x_{j+1}\right)-f\left(x_{j-1}\right)}{x_{j+1}-x_{j-1}} f′(xj)=xj+1−xj−1f(xj+1)−f(xj−1)
为了导出 f f f 导数的近似值 ,我们回到泰勒级数。对于任意函数 f ( x ) f(x) f(x),对于任意函数 f ( x ) f(x) f(x) , f f f 围绕 a = x j a=x_j a=xj 的泰勒级数是 f ( x ) = f ( x j ) ( x − x j ) 0 0 ! + f ′ ( x j ) ( x − x j ) 1 1 ! + f ′ ′ ( x j ) ( x − x j ) 2 2 ! + f ′ ′ ′ ( x j ) ( x − x j ) 3 3 ! + ⋯ f(x)=\frac{f\left(x_j\right)\left(x-x_j\right)^0}{0!}+\frac{f^{\prime}\left(x_j\right)\left(x-x_j\right)^1}{1!}+\frac{f^{\prime \prime}\left(x_j\right)\left(x-x_j\right)^2}{2!}+\frac{f^{\prime \prime \prime}\left(x_j\right)\left(x-x_j\right)^3}{3!}+\cdots f(x)=0!f(xj)(x−xj)0+1!f′(xj)(x−xj)1+2!f′′(xj)(x−xj)2+3!f′′′(xj)(x−xj)3+⋯
如果 x x x 位于间距为 h h h 的点网格上,我们可以计算 x = x j + 1 x=x_{j+1} x=xj+1 处的泰勒级数以获得
f ( x j + 1 ) = f ( x j ) ( x j + 1 − x j ) 0 0 ! + f ′ ( x j ) ( x j + 1 − x j ) 1 1 ! + f ′ ′ ( x j ) ( x j + 1 − x j ) 2 2 ! + f ′ ′ ′ ( x j ) ( x j + 1 − x j ) 3 3 ! + ⋯ f\left(x_{j+1}\right)=\frac{f\left(x_j\right)\left(x_{j+1}-x_j\right)^0}{0!}+\frac{f^{\prime}\left(x_j\right)\left(x_{j+1}-x_j\right)^1}{1!}+\frac{f^{\prime \prime}\left(x_j\right)\left(x_{j+1}-x_j\right)^2}{2!}+\frac{f^{\prime \prime \prime}\left(x_j\right)\left(x_{j+1}-x_j\right)^3}{3!}+\cdots f(xj+1)=0!f(xj)(xj+1−xj)0+1!f′(xj)(xj+1−xj)1+2!f′′(xj)(xj+1−xj)2+3!f′′′(xj)(xj+1−xj)3+⋯
代入 h = x j + 1 − x j h=x_{j+1}-x_j h=xj+1−xj 并求解 f ′ ( x j ) f^{\prime}\left(x_j\right) f′(xj) 得出方程
f ′ ( x j ) = f ( x j + 1 ) − f ( x j ) h + ( − f ′ ′ ( x j ) h 2 ! − f ′ ′ ′ ( x j ) h 2 3 ! − ⋯ ) f^{\prime}\left(x_j\right)=\frac{f\left(x_{j+1}\right)-f\left(x_j\right)}{h}+\left(-\frac{f^{\prime \prime}\left(x_j\right) h}{2!}-\frac{f^{\prime \prime \prime}\left(x_j\right) h^2}{3!}-\cdots\right) f′(xj)=hf(xj+1)−f(xj)+(−2!f′′(xj)h−3!f′′′(xj)h2−⋯)
括号中的项 − f ′ ′ ( x j ) h 2 ! − f ′ ′ ′ ( x j ) h 2 3 ! − ⋯ -\frac{f^{\prime \prime}\left(x_j\right) h}{2!}-\frac{f^{\prime \prime \prime}\left( x_j\right) h^2}{3!}-\cdots −2!f′′(xj)h−3!f′′′(xj)h2−⋯ 被称为 h h h 的高阶项。高阶项可以重写为
− f ′ ′ ( x j ) h 2 ! − f ′ ′ ′ ( x j ) h 2 3 ! − ⋯ = h ( α + ϵ ( h ) ) -\frac{f^{\prime \prime}\left(x_j\right) h}{2!}-\frac{f^{\prime \prime \prime}\left(x_j\right) h^2}{3!}-\cdots=h(\alpha+\epsilon(h)) −2!f′′(xj)h−3!f′′′(xj)h2−⋯=h(α+ϵ(h))
其中 α \alpha α 是某个常数, ϵ ( h ) \epsilon(h) ϵ(h) 是 h h h 的函数,当 h h h 变为 0 时,该函数也变为 0。你可以用一些代数来验证这是真的。我们使用缩写“ O ( h ) O(h) O(h)”来表示 h ( α + ϵ ( h ) ) h(\alpha+\epsilon(h)) h(α+ϵ(h)),并且一般来说,我们使用缩写“ O ( h p ) O\left(h^p\right) O(hp)”来表示 h p ( α + ϵ ( h ) ) h^p(\alpha+\epsilon(h)) hp(α+ϵ(h))
将 O ( h ) O(h) O(h) 代入前面的方程得出
f ′ ( x j ) = f ( x j + 1 ) − f ( x j ) h + O ( h ) f^{\prime}\left(x_j\right)=\frac{f\left(x_{j+1}\right)-f\left(x_j\right)}{h}+O(h) f′(xj)=hf(xj+1)−f(xj)+O(h)
这给出了近似导数的前向差分公式为
f ′ ( x j ) ≈ f ( x j + 1 ) − f ( x j ) h f^{\prime}\left(x_j\right) \approx \frac{f\left(x_{j+1}\right)-f\left(x_j\right)}{h} f′(xj)≈hf(xj+1)−f(xj)
我们说这个公式是 O ( h ) O(h) O(h)。
💦示例:余弦函数 f ( x ) = cos ( x ) f(x)=\cos (x) f(x)=cos(x)。我们知道 cos ( x ) \cos(x) cos(x)的导数是 − sin ( x ) -\sin(x) −sin(x)。尽管在实践中我们可能不知道我们求导的基础函数,但我们使用简单的例子来说明上述数值微分方法及其准确性。以下代码以数值方式计算导数。
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-poster')
%matplotlib inline
h = 0.1
x = np.arange(0, 2*np.pi, h)
y = np.cos(x) forward_diff = np.diff(y)/h
x_diff = x[:-1:]
exact_solution = -np.sin(x_diff) plt.figure(figsize = (12, 8))
plt.plot(x_diff, forward_diff, '--', \label = 'Finite difference approximation')
plt.plot(x_diff, exact_solution, \label = 'Exact solution')
plt.legend()
plt.show()max_error = max(abs(exact_solution - forward_diff))
print(max_error)
0.049984407218554114
如上图所示,两条曲线之间存在微小的偏移,这是由于数值导数求值时的数值误差造成的。两个数值结果之间的最大误差约为 0.05,并且预计会随着步长的增大而减小。
💦示例:以下代码使用递减步长 h h h 的前向差分公式计算 f ( x ) = cos ( x ) f(x)=\cos (x) f(x)=cos(x) 的数值导数。然后,它绘制近似导数和真实导数之间的最大误差与 h h h 的关系,如生成的图形所示。
h = 1
iterations = 20
step_size = []
max_error = [] for i in range(iterations):h /= 2 step_size.append(h) x = np.arange(0, 2 * np.pi, h) y = np.cos(x) forward_diff = np.diff(y)/h x_diff = x[:-1] exact_solution = -np.sin(x_diff) max_error.append(\max(abs(exact_solution - forward_diff)))
plt.figure(figsize = (12, 8))
plt.loglog(step_size, max_error, 'v')
plt.show()
双对数空间中直线的斜率为 1 ;因此,误差与 h 1 h^1 h1成正比,这意味着,正如预期的那样,前向差分公式为 O ( h ) O(h) O(h)。
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python热涨落流体力学求解算法和英伟达人工智能核评估模型
🎯要点 🎯平流扩散简单离散微分算子 | 🎯相场模拟:简单旋节线分解、枝晶凝固的 | 🎯求解二维波动方程,离散化时间导数 🎯英伟达 A100 人工智能核性能评估模型 | 🎯热涨落流体动力学…...
【C语言】数组参数和指针参数详解
在写代码的时候难免要把【数组】或者【指针】传给函数,那函数的参数该如何设计呢? 1 一维数组传参 #include <stdio.h> void test(int arr[])//ok? {} void test(int arr[10])//ok? {} void test(int* arr)//ok? {} void test2(int* arr[20])…...

Tuple 元组
文章目录 一、什么是元组 ?二、元组的具体操作2.1 创建元组2.1.1 tuple() 创建元组函数和 list() 创建列表函数总结 2.2 元组的元素访问操作2.3 元组的元素计数操作2.4 zip 对象 一、什么是元组 ? 列表属于可变序列,可以任意修改列表中的元素。 元组的…...

(资料收藏)王阳明传《知行合一》共74讲,王阳明知行合一音频讲解资料
今天给大家带来的不是软件,而是一份精神食粮——《知行合一》的教程福利。这可不是一般的教程,它关乎心灵,关乎智慧,关乎我们如何在纷繁复杂的世界中找到自己的位置。 咱们得聊聊王阳明,这位明代的大儒,他…...
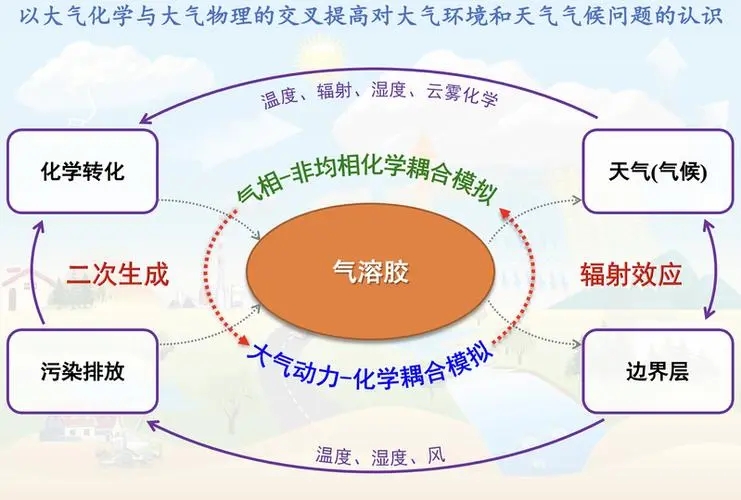
空气质量预报模式系统WRF-CMAQ
空气污染问题日益受到各级政府以及社会公众的高度重视,从实时的数据监测公布到空气质量数值预报及预报产品的发布,我国在空气质量监测和预报方面取得了一定进展。随着计算机技术的高速发展、空气污染监测手段的提高和人们对大气物理化学过程认识的深入&a…...
方法总结)
Collections.sort()方法总结
Collections.sort()方法总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨 Java 中的 Collections.sort() 方法。这个方法是 Java 集合框架中的…...
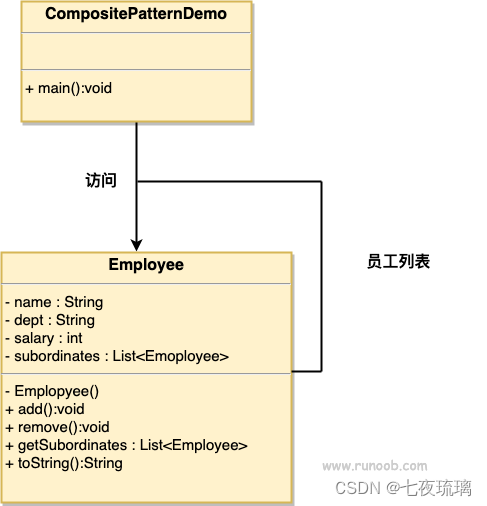
Java23种设计模式(二)
1、单例模式 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保只有…...

Web前端收入来源:探索多元化的盈利渠道
Web前端收入来源:探索多元化的盈利渠道 在数字化时代,Web前端技术日益成为推动互联网业务发展的重要力量。对于前端开发者而言,除了传统的薪资收入外,还存在多种潜在的收入来源。本文将从四个方面、五个方面、六个方面和七个方面…...
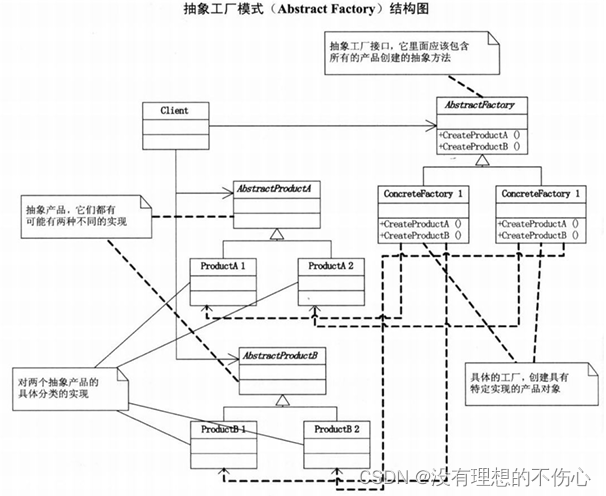
抽象工厂模式(大话设计模式)C/C++版本
抽象工厂模式 C 参考:https://www.cnblogs.com/Galesaur-wcy/p/15927110.html #include <iostream> using namespace std;// 抽象产品Department ,定义具体产品的公共接口 class Department { public:virtual ~Department() default;virtual void Insert()…...

springboot宠物医院信息管理系统-计算机毕业设计源码04164
摘 要 现如今在中国,随着人民生活质量的逐渐提高,以及人民群众消费能力的日渐增长,各种各样的家养小动物,已经逐渐成为人类越来越亲密的生活伴侣。并且,现如今社会竞争及其激烈,人们的生活节奏越发急促、紧…...

Leetcode Hot100之哈希表
1. 两数之和 题目描述 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现思路…...

Vision Transformer with Sparse Scan Prior
摘要 https://arxiv.org/pdf/2405.13335v1 In recent years, Transformers have achieved remarkable progress in computer vision tasks. However, their global modeling often comes with substantial computational overhead, in stark contrast to the human eye’s eff…...

笔记-python 中BeautifulSoup入门
在前面的例子用,我用了BeautifulSoup来从58同城抓取了手机维修的店铺信息,这个库使用起来的确是很方便的。本文是BeautifulSoup 的一个详细的介绍,算是入门把。文档地址:http://www.crummy.com/software/BeautifulSoup/bs4/doc/ …...

Tomcat Websocket应用实例研究
概述 本文介绍了如何根据Tomcat给出的websocket实例,通过对实例的学习,定制自己基于websocket的应用。 环境及版本: Ubuntu 22.04.4 LTSApache Tomcat/10.1.20openjdk 11.0.23 2024-04-16浏览器:Chrome 相关资源及链接 Class…...

leetcode-11-二叉树前中后序遍历以及层次遍历
一、递归版 前序遍历 (先根遍历) 中左右 class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result new ArrayList<Integer>();preorder(root, result);return result;}public void preorder…...
——集合)
Python基础学习笔记(十一)——集合
目录 一、集合的介绍与创建二、集合的存储原理三、元素的修改1. 添加元素2. 删除元素 四、集合的运算五、集合的判定 一、集合的介绍与创建 集合(set),一种可变、无序、不重复的数据结构,由大括号{}内、用逗号分隔的一组元素组成。…...

FineReport
1.FineReport 官网 :FineReport产品简介- FineReport帮助文档 - 全面的报表使用教程和学习资料 下载地址 免费下载FineReport - FineReport报表官网 FineReport是一款用于报表制作,分析和展示的工具。 普通模板:是 FineReport 最常用…...

嵌入式就业前景好么
嵌入式就业前景在当前环境下是较为乐观的,以下是对嵌入式就业前景的详细分析: 广泛应用领域:嵌入式系统广泛应用于智能家居、医疗设备、航空航天等领域。随着物联网(IoT)的快速发展,预计到2024年ÿ…...
为啥找对象千万别找大厂男,还好我不是大厂的。。
网上看到一大厂女员工发文说:找对象千万别找大厂男,理由说了一大堆,无非就是大厂男为了逃避带娃,以加班为由宁愿在工位上玩游戏也不愿回家。当然这种观点有的人赞同有的人反对。 网友精彩评论: --------------下面是今…...

如何查看k8s中service的负载均衡策略
在Kubernetes中,Service的负载均衡策略一般由kube-proxy负责,kube-proxy使用iptables或IPVS规则进行负载均衡。默认情况下,kube-proxy使用的是轮询(Round Robin)策略,但是在使用IPVS模式时,可以…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
