【数据结构与算法】哈夫曼树与哈夫曼编码
文章目录
- 哈夫曼树(最优二叉树)
- 定义
- 举个🌰(WPL的计算)
- 哈夫曼树的构造(最优二叉树的构造)
- 举个🌰
- 哈夫曼树的性质
- 哈夫曼编码
- 定义
- 构造
哈夫曼树(最优二叉树)
在介绍哈夫曼树之前,我们需要介绍一些概念:
-
路径:路径是指从一个结点到另一个结点的之间所经过的所有结点构成的序列。
-
路径长度:路径长度是路径上所经过的边的个数
-
权:在应用树的时候,我们常常会将树的结点赋予一个表示某种意义的数值,这个值称为权。
-
结点的带权路径长度:从根结点到一个结点的路径长度 * 该结点的权值 = 该结点的带权路径长度。
-
树的带权路径长度(WPL):树中所有叶结点的带权路径长度之和称为树的带权路径长度
定义
在含有n个带权叶结点的二叉树中,其中带权路径最小的二叉树称为哈夫曼树,也称最优二叉树。
举个🌰(WPL的计算)

第一棵树的 W P L = 7 ∗ 2 + 5 ∗ 2 + 2 ∗ 2 + 4 ∗ 2 = 36 WPL=7*2+5*2+2*2+4*2=36 WPL=7∗2+5∗2+2∗2+4∗2=36
第二棵树的 W P L = 4 ∗ 2 + 7 ∗ 3 + 5 ∗ 3 + 2 ∗ 1 = 46 WPL=4*2+7*3+5*3+2*1=46 WPL=4∗2+7∗3+5∗3+2∗1=46
第三棵树的 W P L = 7 ∗ 1 + 5 ∗ 2 + 2 ∗ 3 + 4 ∗ 3 = 35 WPL=7*1+5*2+2*3+4*3=35 WPL=7∗1+5∗2+2∗3+4∗3=35
第三颗树的 WPL 恰好是所有含有n个带权叶结点的二叉树中最小的,因此第三棵树为哈夫曼树。
注意:证明一个树是否为哈夫曼树,要看的是所有含有n个带权叶结点的WPL,而不是给几个二叉树选其中WPL最小的。(当然,由于这种证明几乎不可能实现,所以要证明一棵树为哈夫曼树,我们只需要证明它的结构符合最优构造方法即可——因为哈夫曼树并不唯一,例如把一颗哈夫曼树的左右子树交换,它就构成了一棵新的哈夫曼树)。
哈夫曼树的构造(最优二叉树的构造)
给定 n n n 个权值分别为 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn 的结点,构造最优二叉树的方法如下:
- 将这 n n n 个结点视为 n n n 棵只有一个结点的二叉树,它们构成了一个森林 F F F。
- 在森林中选择两颗根节点权值最小的二叉树 T 1 , T 2 T_1,T_2 T1,T2,新增一个结点 N N N,把 T 1 , T 2 T_1,T_2 T1,T2 的根节点作为 N N N 的左、右孩子构成一棵新的二叉树 T 3 T_3 T3, N N N的权值等于 T 1 , T 2 T_1,T_2 T1,T2的根的权值之和。
- 从 F F F 中删除 T 1 , T 2 T_1,T_2 T1,T2,把 T 3 T_3 T3加入到 F F F 中。
- 重复步骤 2 , 3 2,3 2,3,直到 F F F 中只剩下一颗树。
如果对哈夫曼树的构造方法的正确性感兴趣的同学,可以搜一搜哈夫曼树的构造方法的正确性证明。
举个🌰

把这几个叶结点按权值的从小到大排列,有:

选择权值最小的两个结点构成新的二叉树,有:

继续选择两个最小的结点,有:

继续:

这样我们就得到一颗哈夫曼树了
哈夫曼树的性质
- 初始结点最终都为叶结点,并且权值越小的结点到根节点的路径长度越大。
- 因此哈夫曼树的结点总数为 2 ∗ n − 1 2*n-1 2∗n−1,因为构造的过程中新增了n-1个结点(即新增了n-1个分支结点)。
- 哈弗曼树中不存在度为1的结点,因为每次构造都是选择两颗树作为新结点的子节点。
- 哈夫曼树的带权路径长度,等于所有分支结点的权值之和。
哈夫曼编码
在了解哈夫曼编码前,我们先了解一些相关的概念:
- 定长编码:长度固定的编码。
- 变长编码:长度不固定的编码。
- 前缀编码:没有一个编码是另一个编码的前缀,这样的编码叫做前缀编码(显然,根据定义来说,定长编码一定是前缀编码,变长编码不一定是前缀编码)。
对于前缀编码来说,我们可以用树辅助构造前缀编码。
例如:假设要为a,b,c,d四个字符设计二进制前缀编码,那么我们可以用二叉树来辅助构造。
为了使编码能够符合前缀编码的要求,显然,a、b、c、d不会出现在分支结点上。
我们设从任意结点往左边走代表0,从任意结点往右边走代表1,(即指向左子树的边代表0,指向右子树的边代表1)那么a、b、c、d的编码为从根节点到对应叶结点所经过的边代表的值的序列。
我们可以得到如下所示的二叉树:

- a的编码为:0
- b的编码为:10
- c的编码为:110
- d的编码为:111
显然,没有一个编码是另一个编码的前缀,这种编码是前缀编码。
定义
哈夫曼编码是一种变长的二进制前缀编码,它利用哈夫曼树来辅助构造编码,能够非常有效地压缩二进制数据。
构造
我们将每一个字符当做一个独立的结点,其权值等于它出现的次数(或频度),构造一棵哈夫曼树。
设从任意结点指向左子树的边代表0,指向右子树的边代表1或指向左子树的边表示1,指向右子树的边表示0。则各个结点的编码为从根节点到对应结点所经过的边代表的值的序列。
上面的例子就是一个构造哈夫曼编码的案例。
注意:相同结点构造出的哈夫曼树并不唯一,因为它并没有限制到底是左大右小还是右大左小。但相同结点构造出的不同的哈夫曼树的WPL一定是相同的。
同理,哈夫曼编码也是不唯一的。
全篇至此结束,感谢观看。
相关文章:

【数据结构与算法】哈夫曼树与哈夫曼编码
文章目录 哈夫曼树(最优二叉树)定义举个🌰(WPL的计算) 哈夫曼树的构造(最优二叉树的构造)举个🌰 哈夫曼树的性质 哈夫曼编码定义构造 哈夫曼树(最优二叉树) …...

基于多头注意力机制卷积神经网络结合双向门控单元CNN-BIGRU-Mutilhead-Attention实现柴油机故障诊断附matlab代码
在使用这些深度学习库时,你可以按照以下步骤构建CNN-BIGRU-Multihead-Attention模型: 导入所需的库和模块。例如,在使用TensorFlow时,你可以导入tensorflow库和其他需要的模块。 定义输入层。根据你的数据,定义适当的…...

k8s redis 单节点部署
k8s redis 单节点部署kubectl 执行脚本 kubectl --kubeconfig ~/.kube-rz-real/config apply -f redis-leader.yaml -n rz-dt vi redis-leader.yamlapiVersion: apps/v1 kind: Deployment metadata:name: redis-leader-deploylabels:app: redisrole: leadertier: backend sp…...

科普童话投稿
《科普童话》杂志是由国家新闻出版总署批准、黑龙江省教育厅主管、黑龙江省语言文字报刊社主办的正规期刊。《科普童话》以培养科学素养与创新探索精神为办刊宗旨,以科学与艺术统一为编辑方针,以科学教育、教育科学作为自己的出发点,致力于对…...

【Ardiuno】使用ESP32单片机创建web服务通过网页控制小灯开关的实验(图文)
经过实验测试ESP32单片机的网络连接还是很方便的,这里小飞鱼按照程序实例的代码亲自实验一下使用Esp32生成的网页服务来实现远程无线控制小灯开关功能,这样真的是离物联网开发越来越近了,哈哈! 连接好开发板和电路,将…...

百元蓝牙耳机哪款音质最好?四款实力超群机型推荐
在蓝牙耳机市场竞争日益激烈的今天,百元级别的耳机已经具备了令人瞩目的音质表现,对于追求高性价比的消费者来说,如何在众多选项中挑选出一款音质卓越的蓝牙耳机,无疑是一项重要而又充满挑战的任务,今天我将为大家推荐…...
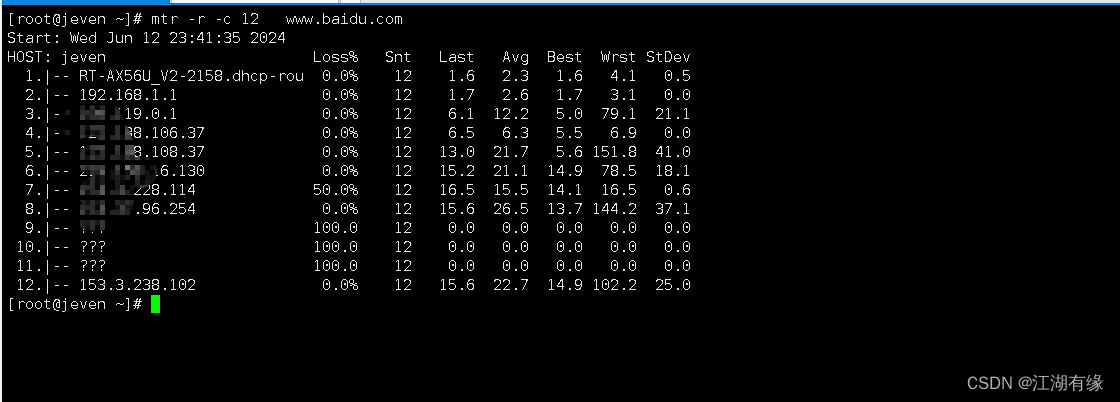
Linux系统之mtr命令的基本使用
Linux系统之mtr命令的基本使用 一、mtr命令介绍二、mtr命令使用帮助2.1 mtr命令的帮助信息2.2 mtr帮助信息解释 三、安装mtr工具四、mtr命令的基本使用4.1 直接使用4.2 设定ping次数4.3 禁用DNS解析4.4 显示IP地址4.5 调整间隔 五、总结 一、mtr命令介绍 mtr命令是一个网络诊断…...

实战tcpdump4.99.4交叉编译
主要是记录交叉编译的一个坑,不知道为什么网上的教程都没遇到过。 环境 libpcap 1.10.4tcpdump 4.99.4WSL 编译步骤 注意事项 注意解压的时候文件夹名需要是libpcap-1.10.4,由于我是在github直接下载zip的压缩包名是libpcap-libpcap-1.10.4.tar.gz解…...
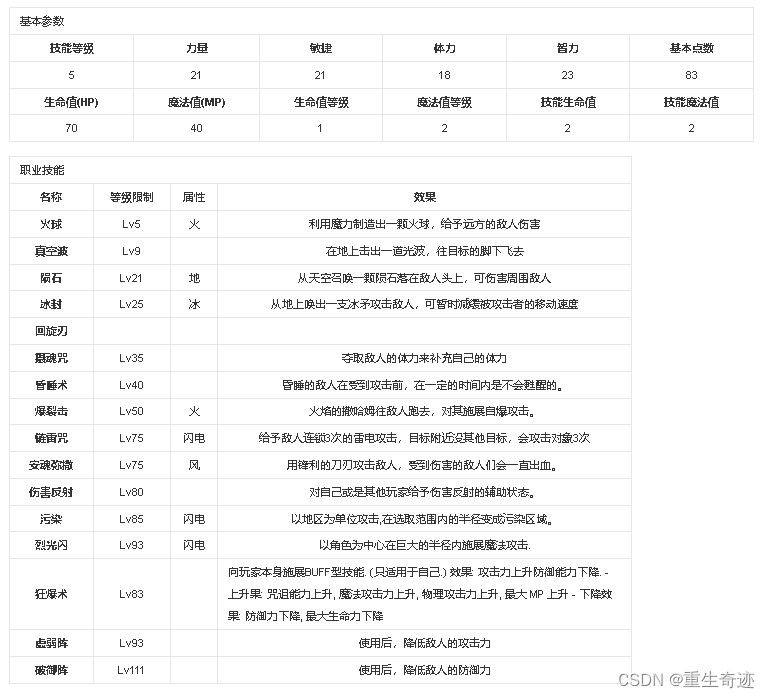
重生奇迹MU召唤术师简介
出生地:幻术园 性 别:女 擅 长:召唤幻兽、辅助魔法&攻击魔法 转 职:召唤巫师(3转) 介 绍:从古代开始流传下来的高贵的血缘,为了种族纯正血缘的延续及特殊使用咒术的天赋&…...
神经网络模型---AlexNet
一、AlexNet 1.导入tensorflow库,这里给简称为tf库 import tensorflow as tf from tensorflow.keras import datasets, layers, modelsdatasets:是用于训练和测试机器学习模型的数据集合 layers:是构建神经网络模型的关键组成部分 models&a…...

corona渲染器与vray比哪个好?支持云渲染平台吗
在视觉渲染技术领域,V-Ray和Corona都以其卓越的性能和广泛应用赢得了高度评价。这两款渲染器各有其独特的优势,使得在它们之间做出选择并非易事。不同的应用场景和用户需求可能会让它们各自展现出不同的优势。 一、corona渲染器跟vray怎么样 在比较V-…...
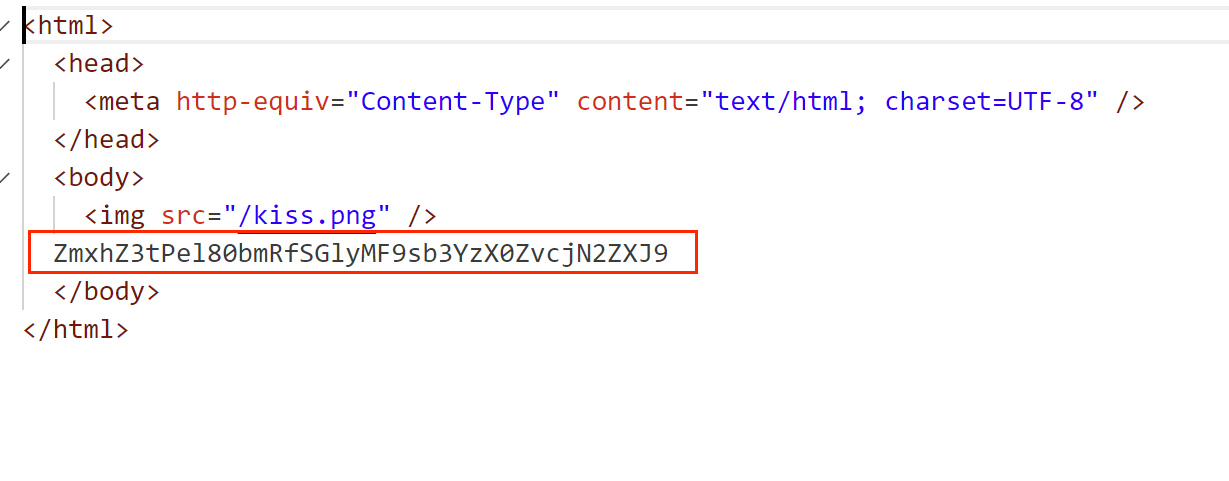
每日一练:攻防世界:Ditf
这是难度1的题吗??? 拿到一个png图片,第一反应就是CRC爆破,结果还真的是高度被修改了 这里拿到一个字符串,提交flag结果发现不是,那么只可能是密钥之类的了 看看有没有压缩包,搜索…...

约瑟夫环递归算法详解与实现
一、引言 约瑟夫环问题是一个著名的理论问题,其背景是在古罗马时期,有n个犯人被围成一个圈,从第一个人开始报数,每次报到m的人将被处决,然后从下一个人开始重新报数,直到所有人都被处决。这个问题可以用递…...
互联网应用主流框架整合之构建REST风格的系统
REST(Representational State Transfer),中文译为“表述性状态转移”,是由Roy Fielding博士在他的博士论文中提出的一种软件架构风格,特别适用于网络应用的设计。REST不是一个标准,而是一种设计原则和约束集…...

vue3-自定义指令来实现input框输入限制
文章目录 前言具体实现分析主要部分详细解析导入和类型定义mounted 钩子函数unmounted 钩子函数指令注册使用 总结 前言 使用vue中的自定义指令来实现input框输入限制 其中关键代码强制触发input ,来避免,输入规则外的字符时,没触发vue的响…...

MySQL日志——redolog
redo log(重做日志) 为什么需要redo log? 在mysql提交一个事务后,这个事务所作的数据修改并不会直接保存到磁盘文件中,而是先保存在buffer pool缓冲区中,在需要读取数据时,先从缓冲区中找&…...

Python热涨落流体力学求解算法和英伟达人工智能核评估模型
🎯要点 🎯平流扩散简单离散微分算子 | 🎯相场模拟:简单旋节线分解、枝晶凝固的 | 🎯求解二维波动方程,离散化时间导数 🎯英伟达 A100 人工智能核性能评估模型 | 🎯热涨落流体动力学…...
【C语言】数组参数和指针参数详解
在写代码的时候难免要把【数组】或者【指针】传给函数,那函数的参数该如何设计呢? 1 一维数组传参 #include <stdio.h> void test(int arr[])//ok? {} void test(int arr[10])//ok? {} void test(int* arr)//ok? {} void test2(int* arr[20])…...

Tuple 元组
文章目录 一、什么是元组 ?二、元组的具体操作2.1 创建元组2.1.1 tuple() 创建元组函数和 list() 创建列表函数总结 2.2 元组的元素访问操作2.3 元组的元素计数操作2.4 zip 对象 一、什么是元组 ? 列表属于可变序列,可以任意修改列表中的元素。 元组的…...

(资料收藏)王阳明传《知行合一》共74讲,王阳明知行合一音频讲解资料
今天给大家带来的不是软件,而是一份精神食粮——《知行合一》的教程福利。这可不是一般的教程,它关乎心灵,关乎智慧,关乎我们如何在纷繁复杂的世界中找到自己的位置。 咱们得聊聊王阳明,这位明代的大儒,他…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
