回溯算法练习题(2024/6/18)
1全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8-10 <= nums[i] <= 10
思路:
这道题目和46.全排列 的区别在与给定一个可包含重复数字的序列,要返回所有不重复的全排列。
这里又涉及到去重了。
1. 递归函数的返回值以及参数
返回值和参数:
void backtracking(vector<int>& nums, vector<bool>& used)- 返回值为
void,因为每次调用只需要修改全局变量path和result,不需要从函数中返回特定值。 - 参数
nums是输入的原始数组,used是一个标记数组,用于记录每个位置的元素是否已经被使用过。
- 返回值为
2. 回溯函数的终止条件
终止条件:
if (path.size() == nums.size())- 当
path的长度等于nums的长度时,表示已经形成了一个完整的排列,将path加入到result中,并返回。
- 当
3. 单层搜索的过程
解题思路:
- 选择路径: 每次递归调用时,在未使用过的元素中选择一个加入到
path中。 - 判断条件: 使用
used数组来判断当前元素是否已经被使用过,以及是否需要去重。 - 标记和递归:
- 将当前未使用的元素加入
path中,并标记为已使用。 - 递归调用
backtracking,继续向下一层搜索。 - 在递归返回后,执行回溯操作:撤销选择,恢复标记状态,以便进行下一次选择。
- 将当前未使用的元素加入
去重部分
去重条件:
if (i > 0 && nums[i - 1] == nums[i] && used[i - 1] == true)- 当前元素与上一个元素相同,并且上一个元素已经被使用过时,跳过当前元素,避免重复选择相同的元素。
代码:
#include <vector>
#include <algorithm> // 包含排序函数 sort
using namespace std;class Solution {
private:vector<int> path; // 存储当前路径的一维向量vector<vector<int>> result; // 存储最终结果的二维向量// 回溯函数,参数为原始数组nums和标记数组usedvoid backtracking(vector<int>& nums, vector<bool>& used) {// 当路径长度等于数组长度时,将当前路径加入结果集合if (path.size() == nums.size()) {result.push_back(path);return;}// 遍历数组numsfor (int i = 0; i < nums.size(); i++) {// 如果元素已经被使用过,则跳过if (i > 0 && nums[i - 1] == nums[i] && used[i - 1] == true) {continue; // 去重部分:跳过重复的元素}if (used[i] == true) {continue; // 如果元素已经被使用过,则跳过}// 标记当前元素为已使用used[i] = true;// 将当前元素加入路径中path.push_back(nums[i]);// 递归进入下一层决策树backtracking(nums, used);// 回溯操作,撤销选择used[i] = false;path.pop_back();}}public:// 主函数,生成所有排列的入口函数vector<vector<int>> permuteUnique(vector<int>& nums) {result.clear(); // 清空结果集合path.clear(); // 清空当前路径sort(nums.begin(), nums.end()); // 排序输入数组,确保重复元素相邻vector<bool> used(nums.size(), false); // 标记数组,记录每个位置的元素是否被使用过// 调用回溯函数,从第一个位置开始生成排列backtracking(nums, used);// 返回最终的结果集合return result;}
};2 N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
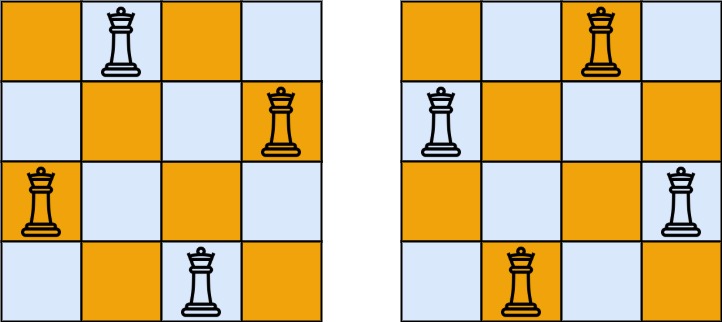
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
思路:
1. 递归函数的返回值以及参数
递归函数 backtracking 的目的是在棋盘上逐行放置皇后,并检查每一步是否符合规则。其参数包括 int n(棋盘大小),int row(当前处理的行数),vector<string>& chessboard(当前棋盘状态)。它没有显式的返回值,而是通过修改全局变量 result 来存储所有合法的解。
2. 回溯函数终止条件
在 backtracking 函数中,终止条件是当 row 等于 n 时,即所有行都处理完毕,此时找到了一个合法的皇后布局,将其加入 result 数组中。
if (row == n) {result.push_back(chessboard); // 找到一种解法,存入结果return;
}
3. 单层搜索的过程
在每一层递归中,通过循环尝试将皇后放置在当前行的每一个列上,然后递归处理下一行。在尝试放置之前,通过 isValid 函数检查当前位置是否合法,避免皇后之间的冲突。
for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) {chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard); // 递归处理下一行chessboard[row][col] = '.'; // 回溯,撤销皇后}
}
这种方法通过逐行放置皇后,并通过回溯撤销不符合条件的放置,最终找到所有合法的N皇后布局。
代码:
class Solution {
private:vector<vector<string>> result; // 存放最终的结果// 回溯算法核心函数// n 是棋盘大小,row 是当前递归到的行数,chessboard 是当前的棋盘状态void backtracking(int n, int row, vector<string>& chessboard) {// 如果已经递归到最后一行,说明找到了一种解法,将其存入结果集合中if (row == n) {result.push_back(chessboard);return;}// 遍历当前行的每一列,尝试放置皇后for (int col = 0; col < n; col++) {// 检查当前位置是否可以放置皇后if (isValid(row, col, chessboard, n)) { // 验证合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard); // 递归处理下一行chessboard[row][col] = '.'; // 回溯,撤销皇后}}}// 检查当前位置是否可以放置皇后bool isValid(int row, int col, vector<string>& chessboard, int n) {// 检查列是否有皇后冲突for (int i = 0; i < row; i++) {if (chessboard[i][col] == 'Q') {return false;}}// 检查左上方是否有皇后冲突for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 检查右上方是否有皇后冲突for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;}public:vector<vector<string>> solveNQueens(int n) {result.clear(); // 清空结果集vector<string> chessboard(n, string(n, '.')); // 初始化棋盘,全部用'.'表示空backtracking(n, 0, chessboard); // 从第一行开始递归求解return result; // 返回所有解法}
};3. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
思路:
1. 递归函数的返回值与参数
递归函数 backtracking 的目标是填充数独中的空白格子(用’.'表示),使得每个数字都符合数独的规则(每行、每列、每个3x3子数独内都不能有重复的数字)。具体来说:
- 参数: 函数接受一个二维字符数组
board,即数独的当前状态。 - 返回值: 返回一个布尔值,表示是否找到了符合规则的解(找到解返回
true,否则返回false)。
2. 回溯函数的终止条件
在 backtracking 函数中,回溯的终止条件包括:
- 当找到一个空白格子(‘.’)时,尝试填入数字’1’到’9’。
- 对于每个尝试的数字,使用
isValid函数检查其在当前位置是否符合数独规则。 - 如果找到一个有效的数字,则将其放入当前格子中,并递归地调用
backtracking继续填充下一个空白格子。 - 如果当前尝试的数字不能使得数独的解合法,则撤销当前的选择(回溯),尝试下一个数字。
3. 单层搜索的过程(解题思路)
在单层搜索的过程中:
- 遍历数独的每个格子,对于每个空白格子尝试填入数字’1’到’9’。
- 使用
isValid函数来检查填入的数字是否在当前行、当前列和当前3x3子数独内都没有重复出现。 - 如果找到一个合法的填入方式,则继续递归填充下一个空白格子;如果找不到合法的填入方式,则进行回溯。
- 当所有空白格子都被填满且符合数独规则时,数独问题得到解决。
判断一个数独棋盘是否合法,主要依据以下三个维度进行检查:
-
同行是否重复:
- 对于每一行,检查其中的每个数字是否唯一。遍历每一行,使用一个集合或者数组来记录已经出现过的数字,若再次出现相同数字则表示该行不合法。
-
同列是否重复:
- 对于每一列,检查其中的每个数字是否唯一。遍历每一列,同样使用集合或数组记录已经出现过的数字,如果重复出现则该列不合法。
-
9宫格是否重复:
- 数独棋盘被分为9个3x3的子宫格。对于每个子宫格,检查其中的数字是否唯一。通过计算当前位置所在的子宫格的起始行和起始列(使用
(row / 3) * 3和(col / 3) * 3计算),遍历该子宫格内的所有数字,同样使用集合或数组来记录已经出现过的数字,若有重复则该子宫格不合法。
- 数独棋盘被分为9个3x3的子宫格。对于每个子宫格,检查其中的数字是否唯一。通过计算当前位置所在的子宫格的起始行和起始列(使用
代码:
class Solution {
private:// 回溯函数,尝试解决数独问题bool backtracking(vector<vector<char>>& board) {// 遍历整个数独表格for(int i = 0; i < board.size(); i++) {for(int j = 0; j < board[0].size(); j++) {// 如果当前位置是空白格if(board[i][j] == '.') {// 尝试填充数字1到9for(char k = '1'; k <= '9'; k++) {// 如果当前数字k在位置(i, j)合法if(isValid(i, j, k, board)) {board[i][j] = k; // 放置数字k// 递归调用backtracking,尝试填充下一个空白格if(backtracking(board)) return true;board[i][j] = '.'; // 回溯,撤销当前位置的填充}}return false; // 1-9都尝试过,无解}}}return true; // 数独已解}// 检查在位置(row, col)填充字符val是否合法bool isValid(int row, int col, char val, vector<vector<char>>& board) {// 检查同一行是否有重复for(int i = 0; i < 9; i++) {if(board[row][i] == val) {return false;}}// 检查同一列是否有重复for(int j = 0; j < 9; j++) {if(board[j][col] == val) {return false;}}// 检查同一个3x3子数独内是否有重复int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for(int i = startRow; i < startRow + 3; i++) {for(int j = startCol; j < startCol + 3; j++) {if(board[i][j] == val) {return false;}}}return true; // 合法}public:// 解决数独问题的入口函数void solveSudoku(vector<vector<char>>& board) {backtracking(board); // 调用回溯函数解决数独}
};相关文章:

回溯算法练习题(2024/6/18)
1全排列 II 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2: 输入:nums [1,2,3] 输出:[[1,…...
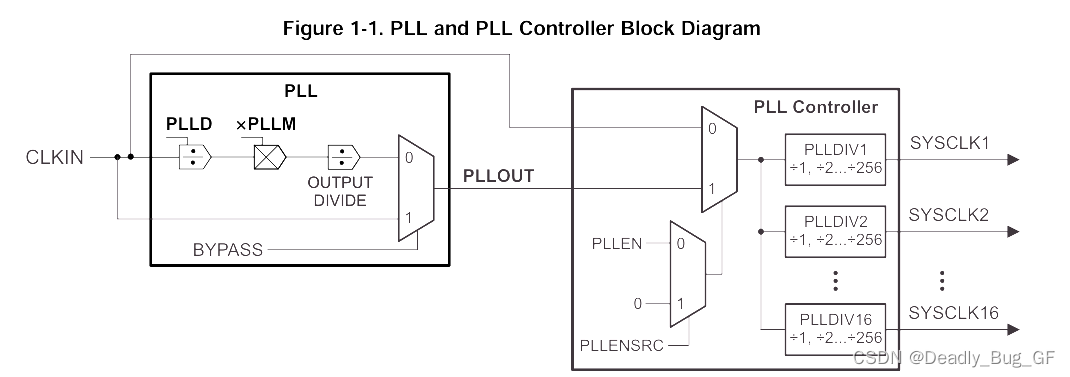
DSP——从入门到放弃系列2——PLL锁相环(持续更新)
1、概述 锁相环(Phase Locked Loop,PLL)是处理器的时钟源,控制着C6678处理器中C66x内核、各外围设备的时钟的时钟比、对准和选通功能。 2、功能描述 上图显示了PLL和PLL控制器的逻辑实现。PLL控制器提供通过软件可配置的分频器࿰…...

Altair 人工智能技术助力MABE预测消费者行为,实现设备性能优化
主要看点 行业: 家电行业 挑战: 企业面临的挑战是如何利用已收集的大量数据,深入了解消费者在产品使用过程中对某些保鲜程序的影响。 Altair 解决方案: Altair采用了Altair RapidMiner人工智能平台来解决问题,特别是…...

解决Spring Boot项目中数据源URL属性的问题
今天测试Springboot项目的时候,报错: . ____ _ __ _ _/\\ / ____ __ _ _(_)_ __ __ _ \ \ \ \ ( ( )\___ | _ | _| | _ \/ _ | \ \ \ \\\/ ___)| |_)| | | | | || (_| | ) ) ) ) |____| .__|_| |_|_| |_\__, | / / / /|_||___…...

Java每日作业day6.18
ok了家人们今天我们继续学习方法的更多使用,闲话少叙,我们来看今天学了什么 1.重载 在同一个类中,可不可以存在同名的方法?重载:在同一个类中,定义了多个同名的方法,但每个方法具有不同的参数类型或参数个…...
mac如何检测硬盘损坏 常用mac硬盘检测坏道工具推荐
mac有时候也出现一些问题,比如硬盘损坏。硬盘损坏会导致数据丢失、系统崩溃、性能下降等严重的后果,所以及时检测和修复硬盘损坏是非常必要的。那么,mac如何检测硬盘损坏呢?有哪些常用的mac硬盘检测坏道工具呢? 一、m…...

怎么通俗理解概率论中的c r(cramer rao 克拉默拉奥)不等式?
还是推一下比较好记 视频链接 【数理统计学重要定理证明:C-R不等式——无偏估计的方差下界-哔哩哔哩】 https://b23.tv/4gk1AvU 【数理统计学重要定理证明:C-R不等式——无偏估计的方差下界-哔哩哔哩】...

Flask之模板
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 目录 一、模板的基本用法 1.1、创建模板 1.2、模板语法 1.3、渲染模板 二、模板辅助工具 2.1、上下文 2.2、全局对象 2.3、过滤器 2.4、测试…...

如何优化 Bash 脚本的执行效率?
要优化 Bash 脚本的执行效率,可以考虑以下几个方面: 减少命令执行次数:Bash 脚本中的命令执行是比较耗时的,在可能的情况下,可以尽量减少命令的执行次数。例如,可以将多个命令合并成一个,使用管…...
c语言---循环 、判断基础知识详解
if语句 else离最近的if语句结合。 if语句题目 //1. 判断一个数是否为奇数 //2. 输出1 - 100之间的奇数 #include <stdio.h> int main() {int n 0;scanf("%d", &n);if (n % 2){printf("奇数\n");}else{printf("不是奇数\n"…...
Opencv高级图像处理
文章目录 Opencv高级图像处理图像坐标二值化滤波高斯滤波中值滤波 开闭运算检测霍夫圆检测边缘检测Canny边缘检测findContours区别傅里叶变换-高/低通滤波 直线检测 相机标定视频处理视频格式 模板摄像头处理(带参调节)单图片处理(带参调节&a…...
Linux操作系统学习:day03
内容来自:Linux介绍 视频推荐:[Linux基础入门教程-linux命令-vim-gcc/g -动态库/静态库 -makefile-gdb调试]( 目录 day0317、创建删除目录创建目录删除目录 18、文件的拷贝19、mv 命令20、查看文件内容的相关命令21、给文件创建软连接或硬链接 day03 …...
快排(霍尔排序实现+前后指针实现)(递归+非递归)
前言 快排是很重要的排序,也是一种比较难以理解的排序,这里我们会用递归的方式和非递归的方式来解决,递归来解决是比较简单的,非递归来解决是有点难度的 快排也称之为霍尔排序,因为发明者是霍尔,本来是命名…...

客户端输入网址后发生的全过程解析(协议交互、缓存、渲染)
目录 1. 输入 URL 并按下回车键2. DNS 解析3. TCP 连接4. 发送 HTTP 请求5. 服务器处理请求6. 发送 HTTP 响应7. 浏览器接收响应8. 渲染网页9. 执行脚本10. 处理其他资源11. TLS/SSL 加密(如果使用 HTTPS)握手过程 12. 协议协商和优化 总结 1. 输入 URL …...

未来科技:Web3如何重塑物联网生态系统
随着Web3技术的崛起,物联网(IoT)的发展正迎来一场深刻的变革。本文将深入探讨Web3如何重塑物联网生态系统,从技术原理到应用实例,全面解析其对未来科技发展的影响和潜力。 1. Web3技术简介与发展背景 Web3技术是建立在…...

C++之模板(二)
1、类模板 2、使用类模板 类模板在使用的时候要显示的调用是哪种类型,而不是像函数模板一样能够根据参数来推导出是哪种类型。 Stack.h #include <stdexcept>template <typename T> class Stack { public:explicit Stack(int maxSize);~Stack();void …...

相机的标定
文章目录 相机的标定标定步骤标定结果影响因素参数分析精度提升一、拍摄棋盘格二、提升标定精度 标定代码实现 相机的标定 双目相机的标定是确保它们能够准确聚焦和成像的关键步骤。以下是详细的标定步骤和可能的结果,同时考虑了不同光照条件和镜头光圈大小等因素对…...
C# 利用XejeN框架源码,编写一个在 Winform 界面上的语法高亮的编辑器,使用 Monaco 编辑器
析锦基于Monaco技术实现的Winform语法高亮编辑器 winform中,我们有时需要高亮显示基于某种语言的语法编辑器。 目前比较强大且UI现代化的,无疑是宇宙最强IDE的兄弟:VS Code。 类似 VS Code 的体验,可以考虑使用 Monaco Editor&a…...

03- jQuery事件处理和动画效果
1. jQuery的事件处理 1.1 绑定事件处理函数 on() 将一个或多个事件的处理方法绑定到被选择的元素上。on()方法适用于当前或未来的元素,如用脚本创建的新元素。 $(selector).on(event,childSelector,data,function) 参数描述event必需。规定要从被选元素添加的一…...
RabbitMQ 入门
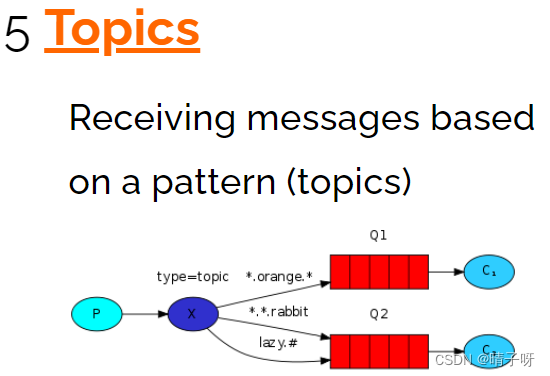
目录 一:什么是MQ 二:安装RabbitMQ 三:在Java中如何实现MQ的使用 RabbitMQ的五种消息模型 1.基本消息队列(BasicQueue) 2.工作消息队列(WorkQueue) 3. 发布订阅(Publish、S…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
