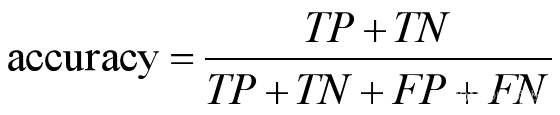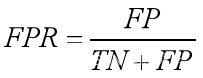【机器学习】第2章 线性回归及最大熵模型
一、概念
1.回归就是用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程称为回归。
2.一个自变量 叫 一元线性回归,大于一个自变量 叫 多元线性回归。
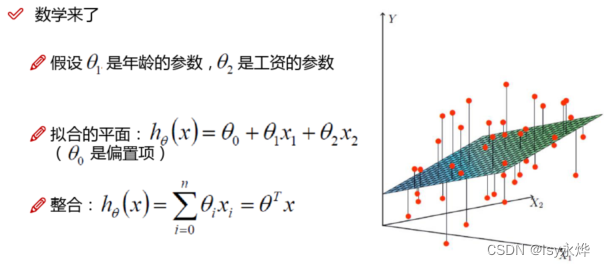
(1)多元回归:两个x,一个y
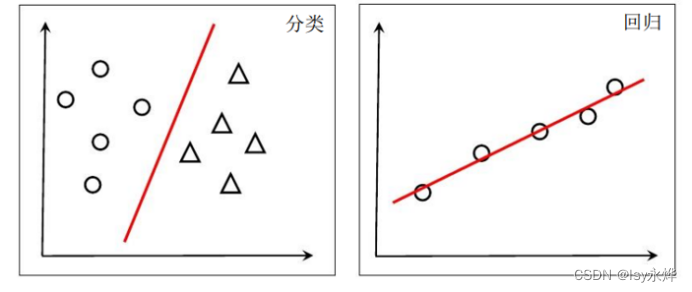
3.这里讲一下线性模型,在二维上就是那根线叫线性模型,他可以用作分类,也可以用作回归:
4. 公式:
(1)准确的说是求 右边的欧米伽和b(用最小二乘法 或者 梯度下降法 求解)。
(2)优化目标:让 【(预测值与真实值之间的欧式距离,下一章)之和】 最小。
预测值就是通过我们用方法推测出的一个点。
真实值就是实际存在的原来样本的一个点,或者说是预测出来本应该是这个点。
5.广义线性模型:
你可以把y替换成lny,原理就跟高中数学里面学的,两边同时取e,最后式子其实是没变化的,这里原理懂了秒懂,不懂得应该也不考无所谓。
6.对率回归 是分类学习算法。其衍生出来的逻辑回归虽然名字中有“回归”,但其主要用途是解决分类问题,特别是二分类问题。
7.梯度下降法简单来说就是一点点求要求的那条直线。
8.人为设置的,而非用来学习的参数,所以叫做超参数。
9.最大熵模型
现实中,不加约束的事物都会朝着“熵增”(不确定,混乱)的方向发展,
当随机变量呈均匀分布时,熵值最大。
最大熵模型就是认为在满足所有约束条件下,熵最大最好(即该情况下数据随机分布,此时最随机,最混乱)。
OK,上面的都不是重点,重点来了:
混淆矩阵
1.基础值缩写:
(1)TN(True negative,真阴率):真0
(2)FN(False nagative,假阴率):假0,即被预测错误的1
(3)TP(True positive,真阳率):真1
(4)FP(False positive,假阳率):假1,即被预测错误的0
2.准确率:表示预测正确的结果占总样本的百分比。
3.精确率(查准率):表示在被预测为正的样本中实际为正的样本的概率。意思就是在预测为正样本的结果中,有多少把握可以预测正确,即不要求对的数量,只要求对的精度/正确率。
4.召回率(查全率):表示在实际为正的样本中被预测为正样本的概率。即是不是所有的1全被找出来了,即要求预测对的数量,但是精度就不保证了。
5.PR曲线:以精确率P为纵坐标,以召回率R为横坐标做出的曲线(竖P横R)。
(1)置信度:(P,R)这样一个点就是置信度
(2)置信度阈值:就是设置一个y轴(P)的值,然后上面的是正例,下面的是负例(上正下负),就是画一条横着的线。
(3)图形:
6.ROC曲线:横轴是假阳率(FPR) 纵轴是真阳率(TPR)
(1)假阳率:
(2)真阳率,就是召回率R:
(3)图形:
(4)x越往右,则表示猜错的正例越来越多,y越往上,则表示猜对的正例越来越多,(1,1)表示此时预测样本全为正例。
二、习题
单选题
7. 逻辑回归模型解决( B)问题
A、回归 B、分类 C、聚类 D、推理
多选题
7. 混淆矩阵大多数评价指标的基础,以下哪些数据它主要包括的信息(ABCD )
A、TN B、TP C、FP D、FN
判断题
6. 逻辑回归是一种广义线性回归,通过回归对数几率的方式将线性回归应用于分类任务。(T)
7. 信息论中,熵可以度量随机变量的不确定性。现实世界中,不加约束的事物都会朝着“熵增”的方向发展,也就是向不确定性增加的方向发展。( T)
8. 准确率可以判断总的正确率,在样本不平衡的情况下,也能作为很好的指标来衡量结果。(F)
相关文章:

【机器学习】第2章 线性回归及最大熵模型
一、概念 1.回归就是用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程称为回归。 2.一个自变量 叫 一元线性回归,大于一个自变量 叫 多元线性回归。 (1)多元回归:两个x,一个…...

科技创新对农业发展的影响
科技创新对农业发展的影响深远且广泛,主要体现在以下几个方面: 一、提高农业生产效率 引入先进的农业机械设备:新型农业机械设备如无人机、机器人等的应用,显著减轻了农民的劳动强度,提高了农作物的种植效率。利用精…...

Linux 常用命令 - rm 【删除文件或目录】
简介 rm 命令源于英文单词 “remove”,它用于删除文件或目录。rm 是 Linux 系统中最基本的命令之一,用于删除指定的文件或目录。默认情况下,rm 不会删除目录,但可以通过递归删除选项来实现。 使用方式 rm [选项]... [文件]...常…...

一血c++
题目描述 每一个竞赛选手都无法拒绝拿一血 "一血"其实就是同学们在榜单上看到的深绿色的标记,代表着某道题目,他是第一个通过的。 叶苡朋老师是一名资深信奥选手,在大学多次获奖,也是一个资深抢一血爱好者࿰…...

无问芯穹Qllm-Eval:制作多模型、多参数、多维度的量化方案
前言 近年来,大语言模型(Large Models, LLMs)受到学术界和工业界的广泛关注,得益于其在各种语言生成任务上的出色表现,大语言模型推动了各种人工智能应用(例如ChatGPT、Copilot等)的发展。然而…...

2024-05-31T08:36:09.000+00:00 转换 YYYY-MM-DD HH-MM-SS
function formatDate(date) {// 处理ISO 8601字符串if (typeof date string) {date new Date(date);}// 处理时间戳else if (typeof date number) {date new Date(date * 1000); // 假设后端时间戳为秒,需要乘以1000转换为毫秒}// 自定义格式化,例如…...
reason: the Java file contained parse errors
今天用Maven打包项目时发生一个错误: file: D:\workspace\echoo2.0-xxx-xxx-portal\src\main\java\com\echoo\service\impl\DecDataServiceImpl.java; reason: the Java file contained parse errors 打包报错显示这个类解析错误 在IDEA中没有任何错误提示 问题所…...
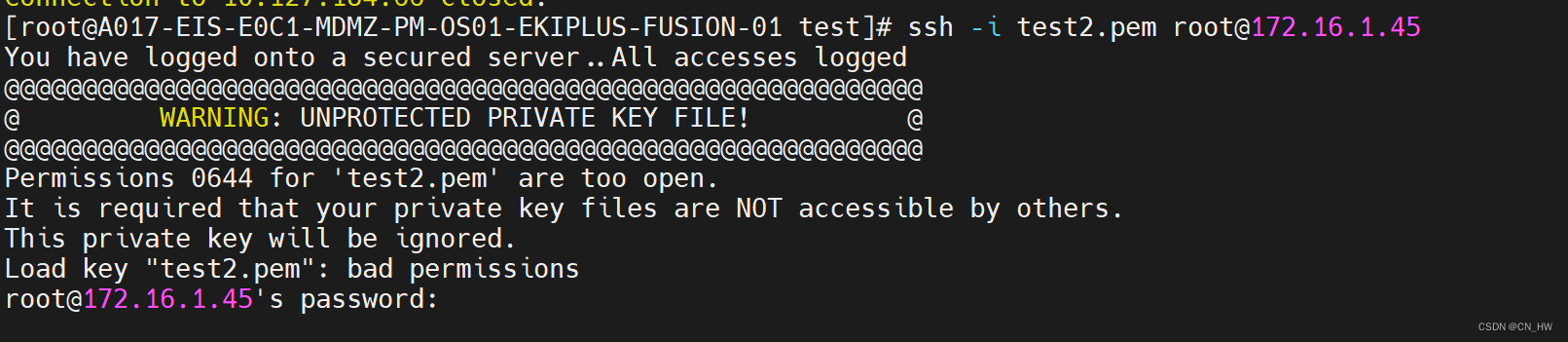
使用密钥对登录服务器
目录 1、使用密钥文件登录服务器 2、登录成功画面: 3、如若出现以下状况,则说明密钥文件登录失败 1、使用密钥文件登录服务器 首先需要上传pem文件 2、登录成功画面: 3、如若出现以下状况,则说明密钥文件登录失败 解决方法&…...

面试_多线程
线程池 线程池的参数有哪些 线程池七大参数分别是corePoolSize、maximumPoolSize、keepAliveTime、unit、workQueue、threadFactory、handler corePoolSize:线程池中常驻核心线程数maximumPoolSize:线程池能够容纳同时执行的最大线程数keepAliveTime&…...
跨境电商必备?揭秘原生IP的作用
一、什么是原生IP? 原生IP(Native IP)是指由互联网服务提供商(ISP)或服务器提供商直接分配给用户的IP地址,这种IP地址直接与用户设备或网络相连,也就是指这个IP的注册地址和服务器机房所在的国…...

mysql竖表变横表不含聚合
文章目录 前言一、vertical_table二、转换1.要将其转换为横表形式,例如:2.sql 总结 前言 在MySQL中将竖表转换为横表(也称为行转列操作),不涉及聚合函数,通常可以通过使用条件判断和自连接来实现。假设有一…...

application/x-www-form-urlencoded和json的区别
application/x-www-form-urlencoded 和 application/json 是两种不同的数据格式,常用于HTTP请求中传递数据。 它们各自的特点和使用场景如下: 1. application/x-www-form-urlencoded •特点:这是一种传统的表单提交时采用的编码类型&#x…...
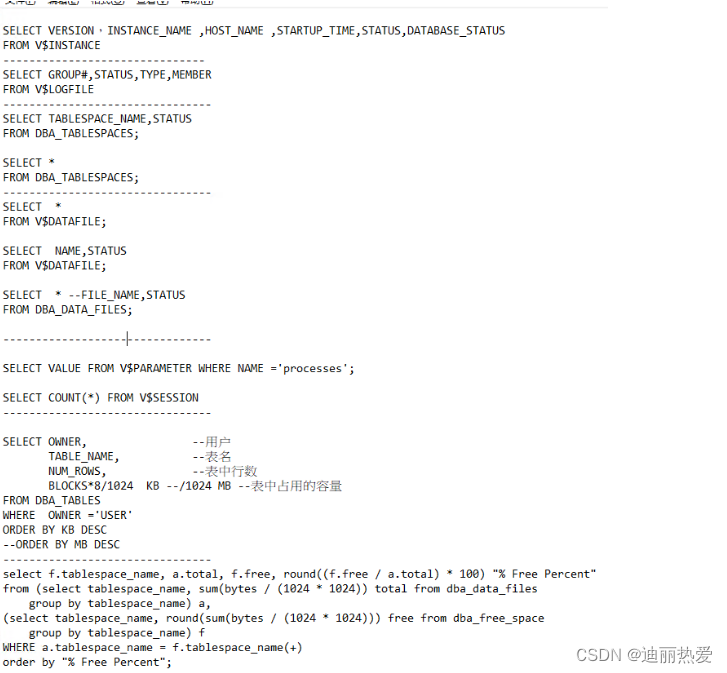
oracle数据库日常保养或巡检语句实践整理汇总
目录 1.目的 2.操作工具 3.实践说明 1.检查Oracle实例状态 2.检查Oracle在线日志状态 3.检查Oracle表空间状态 4.检查Oracle所有数据文件状态 5.检查Oracle数据库连接情况 6.检查Oracle表容量占用大小 7.检查Oracle备份 8.检查数据库表空间的使用情况 4.总结 1.目的 …...

Elasticsearch 第一期:基础的基础概念
前言 Elasticsearch(弹性搜索) ,简称为ES, 它是一个开源的高扩展的分布式全文检索引擎,它提供的功能主要分为:实时存储,实时分析搜索;本身扩展性很好,可以扩展到上百台服…...

MySQL数据库笔记(二)
第一章 单行函数 1.1 什么是函数 函数的作用是把我们经常使用的代码封装起来,需要的时候直接调用即可。这样既提高了代码效率,又提高了可维护性。在SQL中使用函数,极大地提高了用户对数据库的管理效率。 1.2 定义 操作数据对象。 接受参数返回一个结果。 只对一行进行…...

谷歌邮箱:2024年最全使用指南及技巧
注册谷歌邮箱时遇到麻烦了吗?收件箱乱得让人头疼,找不到提升效率的方法?或者是在处理多个谷歌邮箱账户时感到手忙脚乱? 掌握Gmail邮箱的使用技巧是每个外贸人员都必须学会的,本文将提供一个实用的谷歌邮箱注册和使用指…...

工业设计初学者手册——第四部分:制造工艺
工业设计初学者手册 文章目录 工业设计初学者手册第四部分:制造工艺7. 常见制造工艺介绍7.1 传统制造工艺7.2 现代制造工艺 8. 材料选择与应用8.1 材料的基本分类与特性8.2 材料选择的原则8.3 环保材料的应用 总结 第四部分:制造工艺 7. 常见制造工艺介…...

Scala语言:大数据开发的未来之星 - 零基础到精通入门指南
前言 随着大数据时代的到来,数据量的急剧增长为软件开发带来了新的挑战和机遇。Scala语言因其函数式编程和面向对象的特性,以及与Apache Spark的完美协作,在大数据开发领域迅速崛起,成为该领域的新兴宠儿。本篇将从零基础开始&…...
Springboot整合Zookeeper分布式组件实例
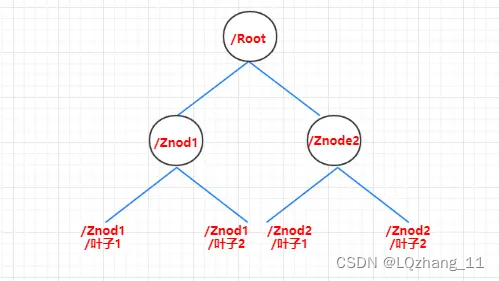
一、Zookeeper概述 1.1 Zookeeper的定义 Zookeeper是一个开源的分布式协调服务,主要用于分布式应用程序中的协调管理。它由Apache软件基金会维护,是Hadoop生态系统中的重要成员。Zookeeper提供了一个高效且可靠的分布式锁服务,以及群集管理…...
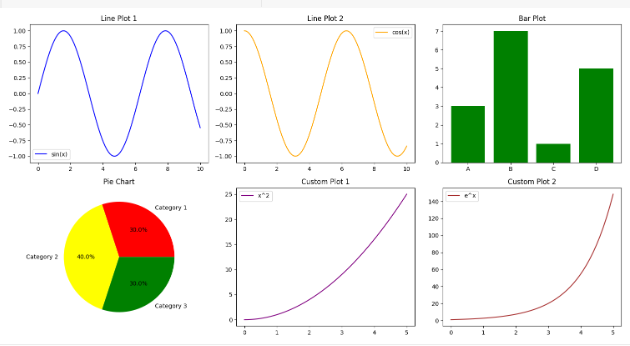
Python | 使用Matplotlib生成子图的示例
数据可视化在分析和解释数据的过程中起着举足轻重的作用。Python中的Matplotlib库提供了一个强大的工具包,用于制作各种图表和图表。一个突出的功能是它能够在单个图中生成子图,为以组织良好和结构化的方式呈现数据提供了有价值的工具。使用子图可以同时…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...