计算机图形学入门16:曲线
1.曲线
曲线(Curves)在图形学中应用非常广泛,比如:相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示,是使用曲线到矢量字体的应用,通过移动一些控制点来改变字体。

2.贝塞尔曲线
2.1 贝塞尔曲线定义
从上图中,如果无限的放大曲线的某一块区域,任何地方都是光滑的。这就是贝塞尔曲线(Bezier Curves)。
贝塞尔曲线是通过一系列控制点进行定义的曲线。而这些控制点满足一些性质,比如要满足从P0点开始,并且沿着P0P1方向,结束沿着P2P3方向,到P3点结束。曲线不必经过所有控制点,但必须经过起始点和结束点。这样就定义了一条贝塞尔曲线,如下图所示。
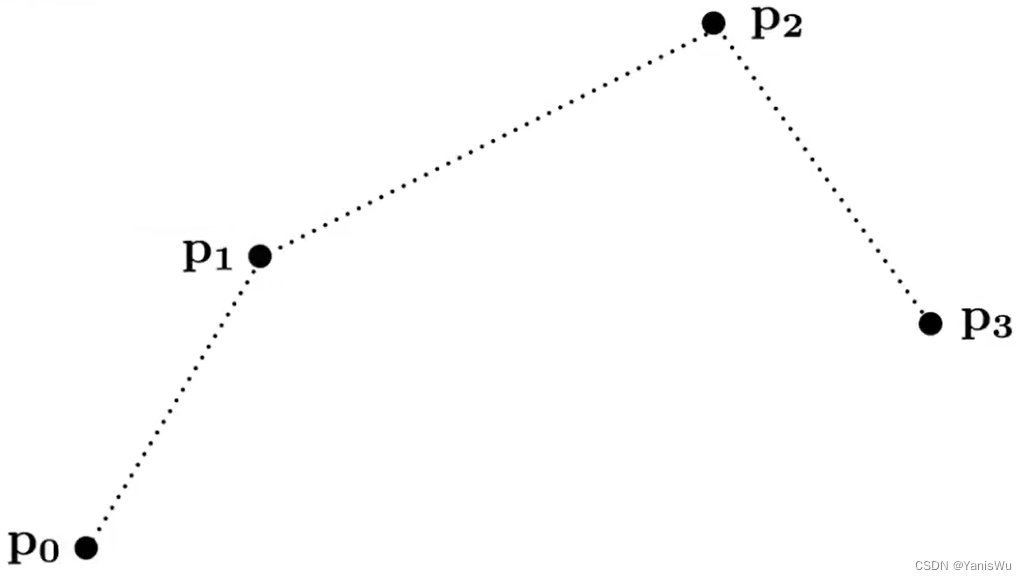
2.2 绘制贝塞尔曲线
那么,如何使用任意点绘制贝塞尔曲线呢?
贝塞尔曲线的绘制算法是 De Casteljau's Algorithm,算法的基本思想是利用线性插值的原理,将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合。
下面,我们以 3 个控制点绘制贝塞尔曲线的例子来进行介绍。
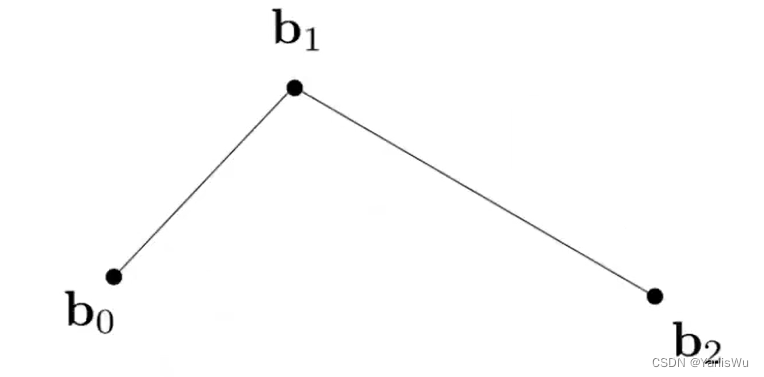
N 个控制点绘制的贝塞尔曲线,称为 N-1 阶贝塞尔曲线。如下图所示,我们定义了 3 个控制点,由此绘制的贝塞尔曲线称之为 二阶贝塞尔曲线(Quadratic Bezier)。对于这 3 个控制点,我们首先对相邻控制点进行连线。
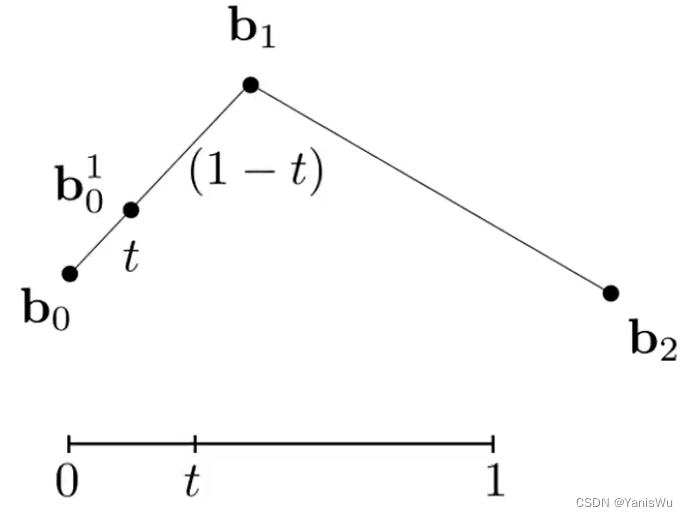
定义一个变量 t,其值的范围为 [0, 1],作为算法的输入值。当 t = 0 时,表示贝塞尔曲线起始点的输入值,当 t = 1 时,表示贝塞尔曲线结束点的输入值。所以算出 t 对应的所有点即可获得别塞尔曲线。
我们在控制点所构成的各个连线上定义一个点,这个点的位置取决于 t 的值,即一个比例值。如下图所示,在 b0b1 线段上定义一个 b10 点,并在 b1b2 线段上定义一个 b11 点。
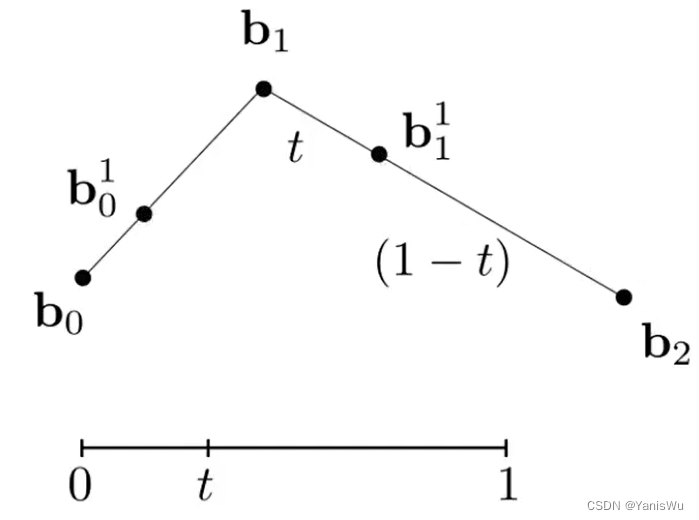
然后,对 b10 点和 b11 点进行连线,按照上述规则,在 b10b11 线段上定义一个 b20 点,找到最后一个点就结束了。如下图所示。

当新定义的点只有一个时,我们可以将 t 的值逐步从 0 变到 1。在这个过程中,b10、b20、b11 的位置都会随着 t 的变化而变化。对于最终的贝塞尔曲线,我们只需要关注最后定义的点 b20 的路径即可。
当我们扩展至更多控制点时,比如 4 个控制点时,我们仍然按照上述规则来处理,将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合,最终绘制曲线。如下图所示。
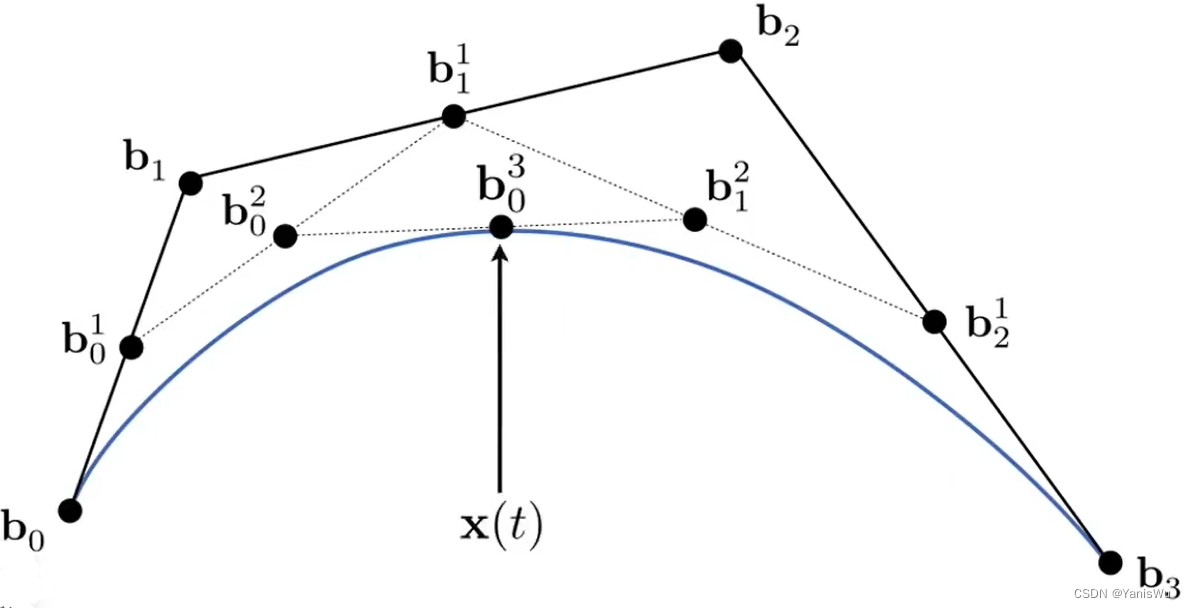
从上述可知,贝塞尔曲线也属于显式几何表示,因为显式几何表示通过直接定义或者参数定义,而这个 t 就是属于参数。
2.3 贝塞尔曲线代数公式
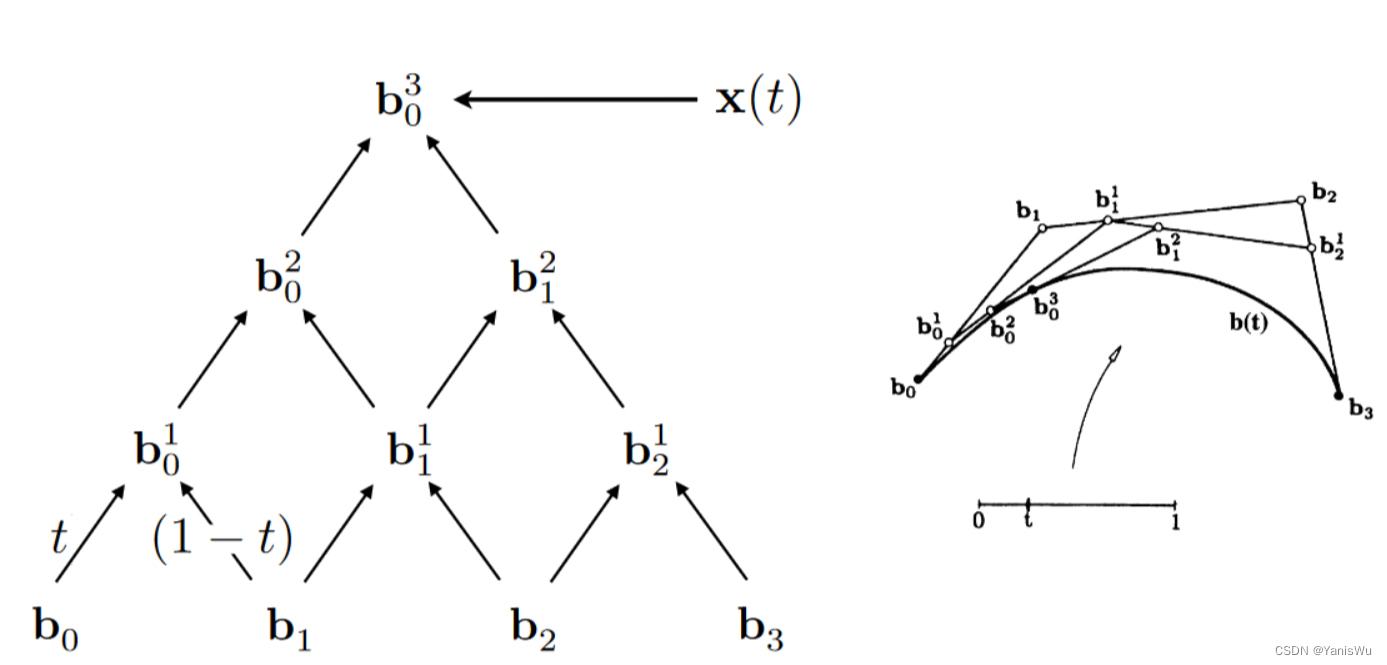
如上图所示,De Casteljau算法给出了一个系数金字塔,从中可知通过不断线性插值得到最后一个值的算法。那么,就可以写出这个关系式,以三个控制点为例,如下图所示。
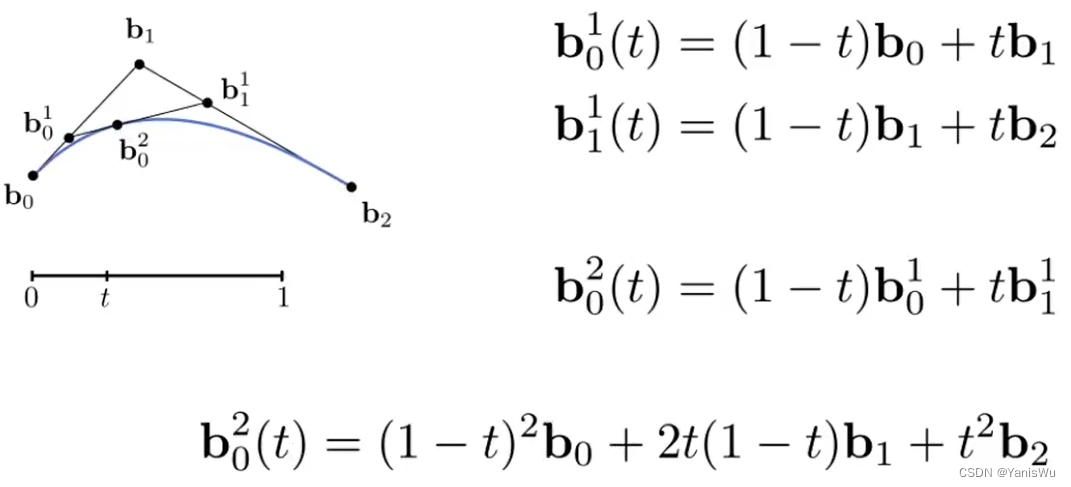
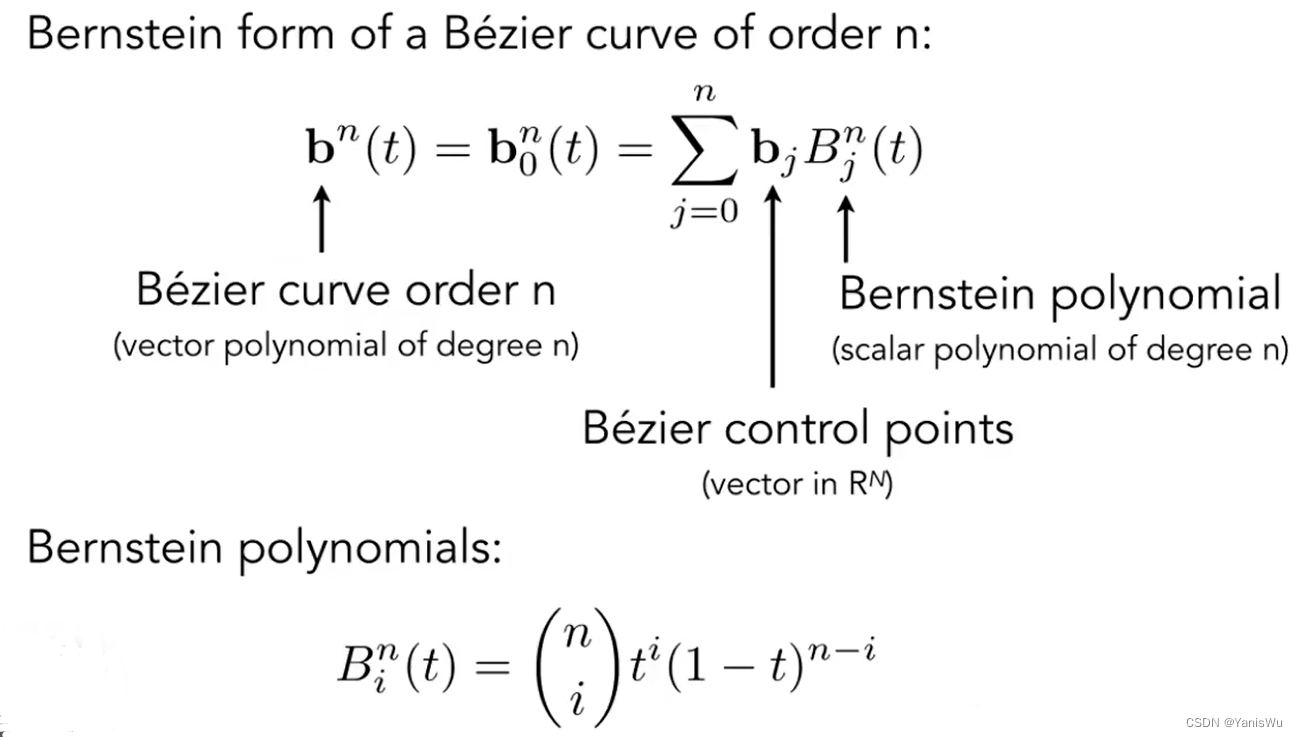
由此,我们可以推导出 N 阶贝塞尔曲线的代数公式,如下图所示。其中,n 表示 N 阶贝塞尔曲线(n+1个控制点), 表示控制点,
为伯恩斯坦多项式(Bernstein Polynomials)。
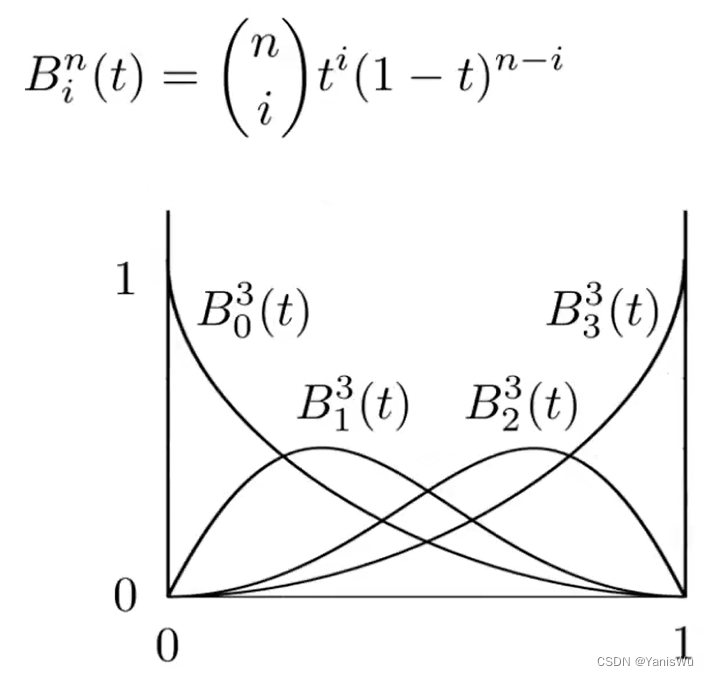
举个例子,假设n=3,那么可以有四个控制点,点的位置不局限于平面上,甚至在三维空间中,展开公式如下。
![]()
对于伯恩斯坦多项式,也可得出如下关系。
2.4 贝塞尔曲线的性质
1.一定过起点和终点。在t=0的时候一定在起点,t=1的时候一定在终点。
![]()
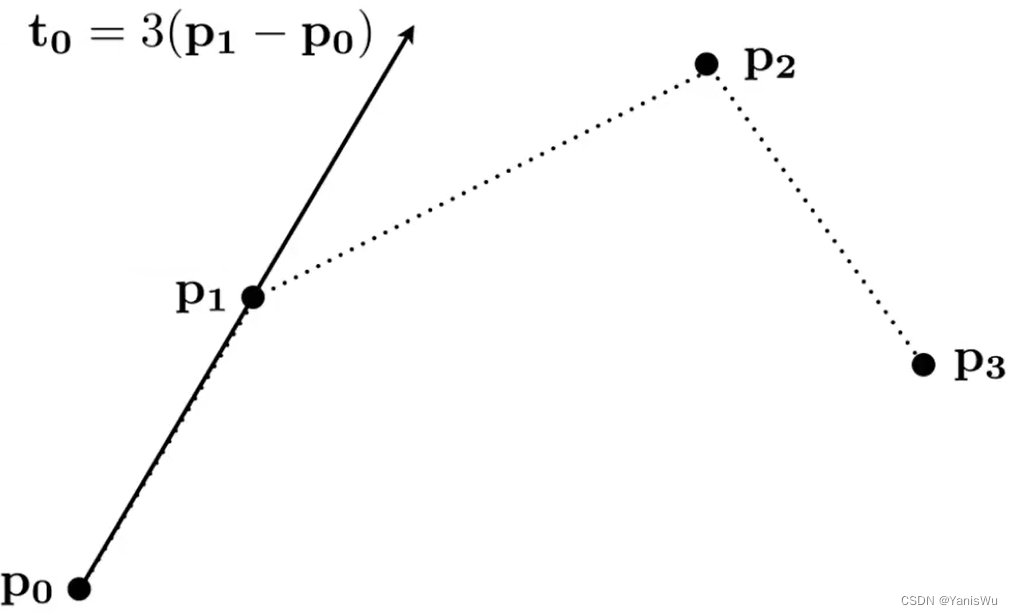
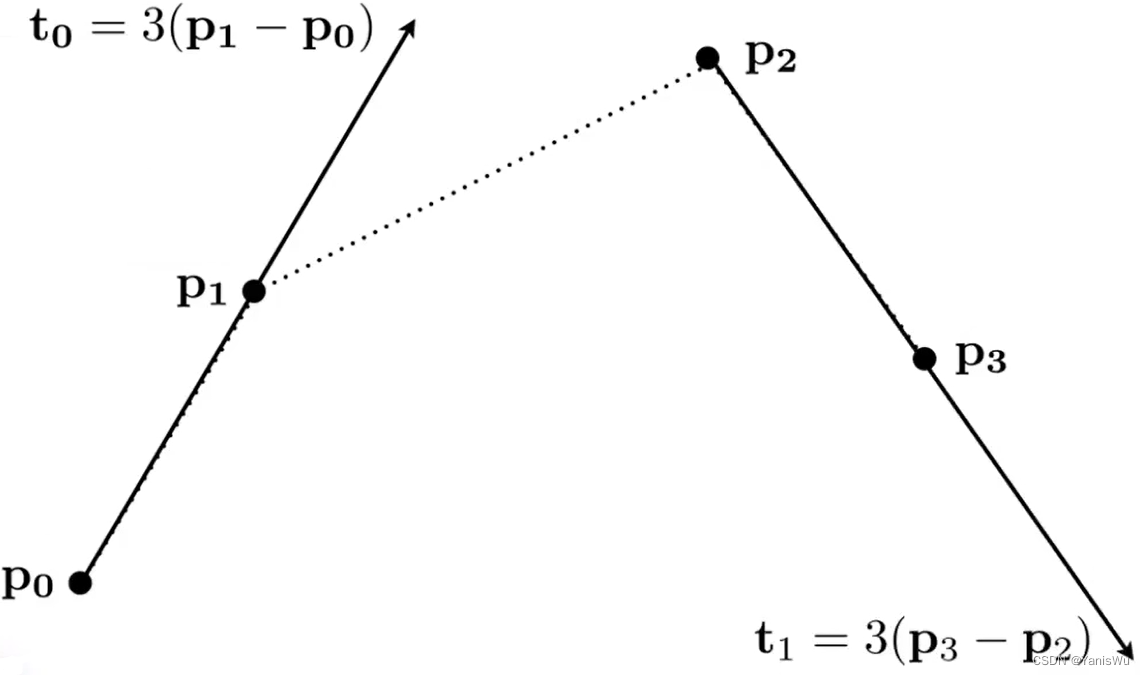
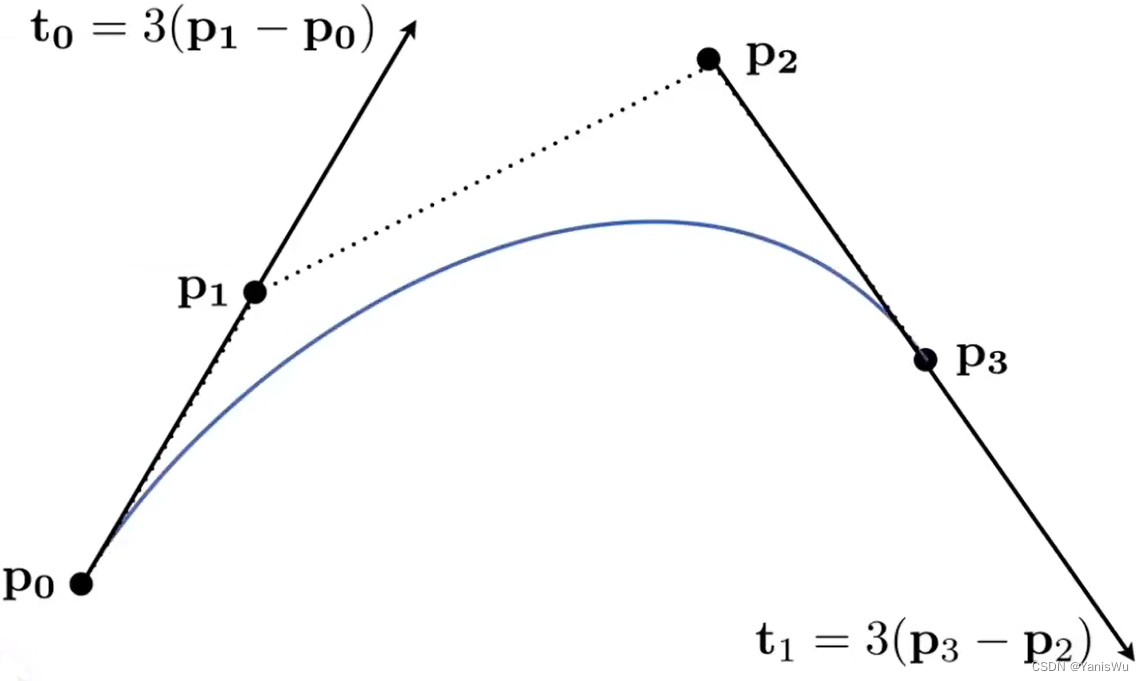
2.起始的切线方向是由起始点和第二个点求出,结束的切线方向是由结束点和倒数第二个点求出。以四个控制举例如下,3倍只是代表4个控制点。
![]()
3.不受仿射变换影响,受投影变换影响。
对贝塞尔曲线上的每个控制点做仿射变换,绘制的新曲线于原曲线一样。
在空间中绘制一条贝塞尔曲线,将控制点投影到相机看到的平面上,然后重新绘制的新曲线与原曲线不同。
4.凸包(Convex Hull)性质:贝塞尔曲线在所有控制点的凸包范围内。如下图所示,蓝色线就是形成的凸包,凸包就是能够包围一系列几何形体的最小的凸多边形。简单理解就是一扇门上订满了钉子,然后用一块橡皮筋将外面一圈包起来,松手后橡皮筋会收缩,收缩后的外框就是凸包。
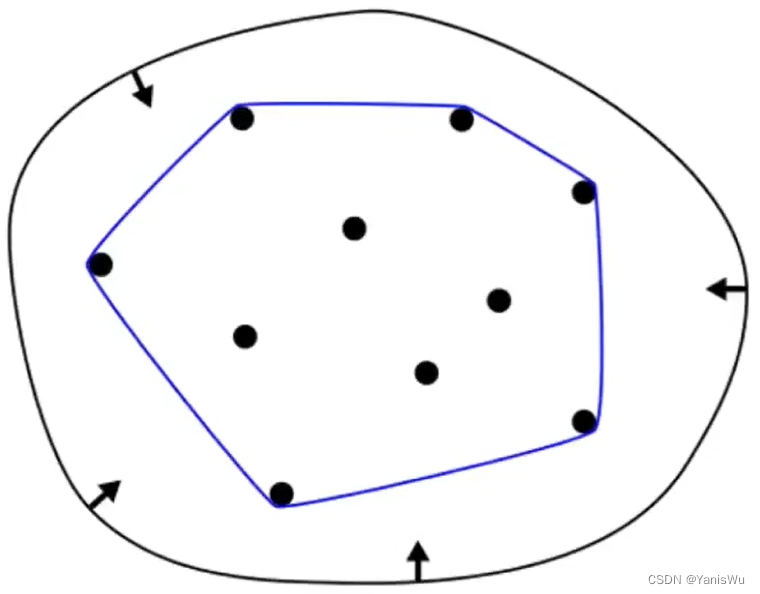
假设有一系列从走到右排列的点,排列在一条线上,这些是绘制贝塞尔曲线的控制点,那么绘制的贝塞尔曲线应该是什么形状?根据凸包性质,这条线就是凸包,而贝塞尔曲线不能超过凸包的范围,贝塞尔曲线被限制在这条线上,所以这条线就是贝塞尔曲线。
3.分段贝塞尔曲线
3.1 定义
如下图所示,给了11个点(n+1),绘制一条贝塞尔曲线(蓝色线)。可以看到这条贝塞尔曲线并不直观,非常平滑,说明当控制点多的时候,贝塞尔曲线很难得到想要的形状。
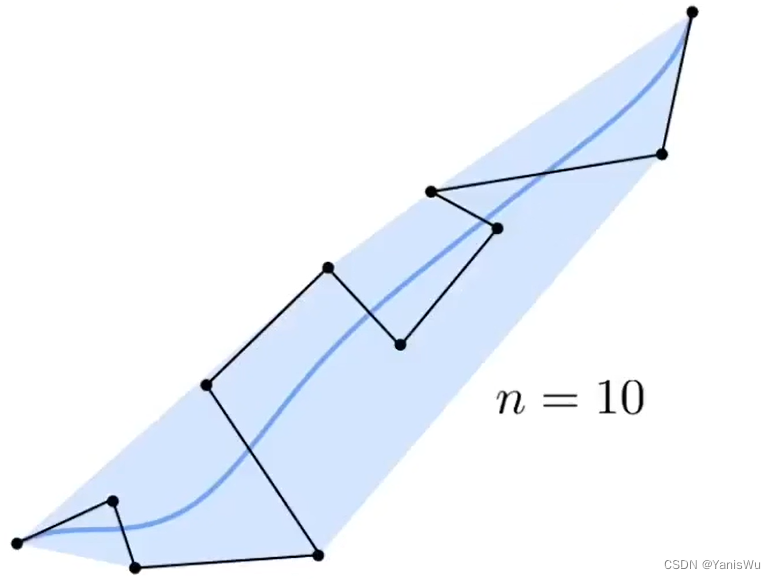
所以,当控制点比较多时,每次用很少的控制点绘制去绘制,然后将绘制的连接成一条贝塞尔曲线。于是就有了分段贝塞尔曲线(Piecewise Bezier Curves),即采用多条贝塞尔曲线进行串联。用4个常控制点来绘制一条贝塞尔曲线,也就是三阶贝塞尔曲线(Cubic Bezier)。如下图所示。

在PS里钢笔工具画曲线就是这个应用。
3.2 平滑处理
如下图所示,是一条分段贝塞尔曲线,而且每4个点绘制一条三次贝塞尔曲线。
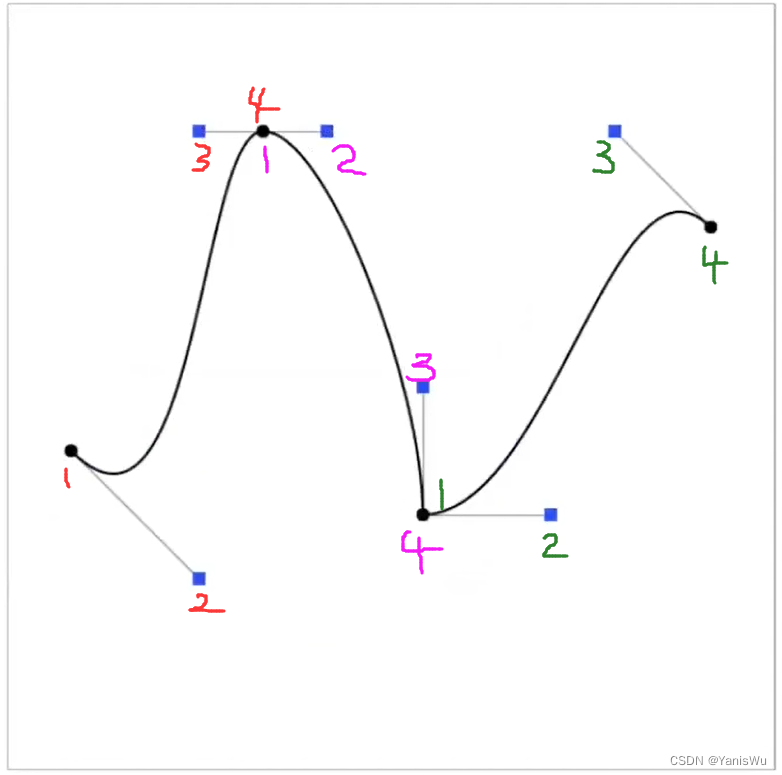
可以发现有连接点的曲线出现了转折,不够平滑,那么如何保证连起来的曲线是平滑的呢?只要保证曲线结束的切线方向与相连曲线起始的切线相同即可(方向大小都相同),也就是导数要连续。
根据贝塞尔曲线的性质:三次贝塞尔曲线的起始切线的方向由第一个点和第二个点求得,结束切线的方向由第三个点和第四个点求出,并且前面有系数3。而相连的两条曲线,前一条曲线的结束点就是后一条曲线的起始点,所以需要调整前一条曲线的第三个点与后一条曲线的第二个点位置,使其切线相同。
3.3 连续性
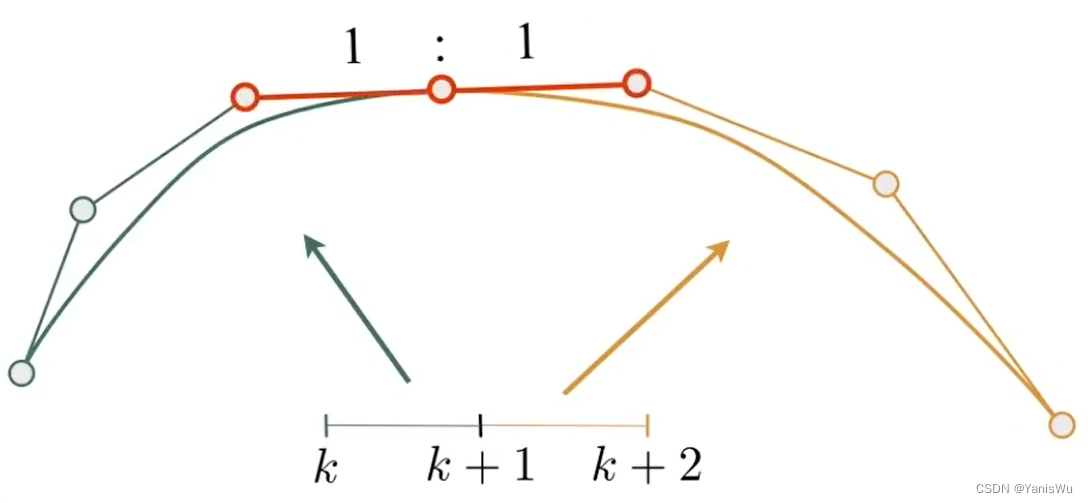
如下图所示,在几何上两条三次贝塞尔曲线相连通过一个控制点,这是一种最简单的连续。像这种第一段的终点等于第二段的起点叫做连续(Continuity)。
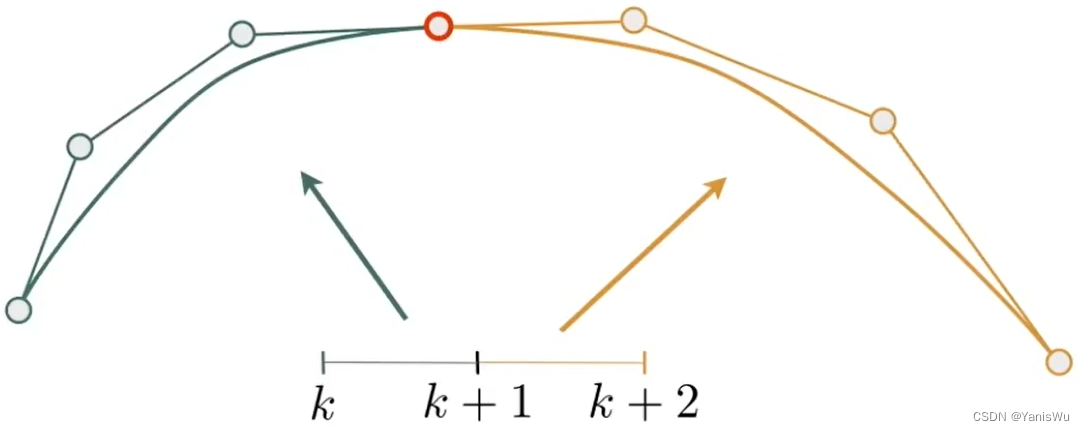
连续关系式:
![]() 。
。表示上一段曲线终点,
表示下一段曲线起点。
那么,在几何连续外,还需要切线的连续(切线相同,方向和大小都相同)。这叫做连续,也就是一阶导数的连续。如下图所示。
连续关系式:
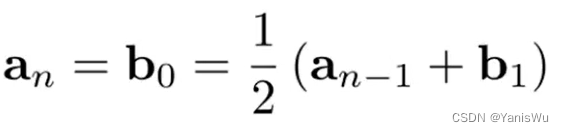 。
。
除了一阶导数连续,还有2阶导数连续,也叫做曲率连续(连续)。
综上, 连续为两个函数在值上连续,
连续为导数上的连续,
为二阶导数连续,以此类推。
4.样条曲线
4.1 定义
样条(Spline)曲线一种连续的曲线,通过一系列的控制点控制,在任意位置满足一定的连续性,也就是一定数量的连续导数(任意阶)。
简而言之,这是一条可控的曲线。

4.2 B样条曲线
B样条(B-Splines)是基础样条(Basis Splines)的缩写,就是基函数样条。可以理解成用伯恩斯坦多项式在时间 t 里几个不同项对不同的控制点做一个加权平均,也可以理解成不同控制点位置对伯恩斯坦多项式进行加权求和。那么,这个伯恩斯坦多项式就可以理解为基函数。基函数就是由不同函数通过不同方式组合起来可以形成别的函数。
B样条曲线相当于是贝塞尔曲线的一个扩展。贝塞尔曲线在控制点很多的情况下,移动其中任何一个点,整个曲线在任何位置都会发生变化。假如只需要移动一个控制点改变一小段曲线的形状,也就是局部性,而B样条曲线能够满足这个功能,比分段贝塞尔曲线更方便。
B样条需要比贝塞尔曲线更多的信息。比贝塞尔曲线更加复杂,这里不做详细介绍。
相关文章:

计算机图形学入门16:曲线
1.曲线 曲线(Curves)在图形学中应用非常广泛,比如:相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示,是使用曲线到矢量字体的应用,通过移动一些控制点来改变字体。 2.贝塞尔曲线 2.1 贝…...
【Ruby基础01】windows和termux中搭建Ruby开发环境
windows下环境搭建 railsinstaller官方git地址 按照文档安装git、nodejs、yarn,安装教程百度一下。railsinstall可以从release页面下载最新版本4.1.0。 安装完成如下 安装RubyMine 下载RubyMine RubyMine下载地址 安装激活 下载文件,按照里面的流程…...

2406c++,iguana动态反射
原文 iguana是一个基于编译期反射的序化库,支持从结构序化到不同数据格式. iguana可序化一个C结构到json,xml,yaml和protobuf格式.这都是通过编译期反射实现的. 现在iguana也支持了动态反射,主要特征: 1,通过对象名创建对象实例 2,取对象所有字段名 3,根据字段名取字段值 4,根…...

干货分享——AB站帮你解决独立站收款难题
目前,国内已经有抖音、拼多多和淘宝平台推出“仅退款”售后服务,无疑是加剧了原本就在疯狂打价格战的国内电商的严峻现状,使得商家不得不担心被顾客“薅羊毛”。在国内电商环境严重“内卷”的情况下,拓宽海外市场不失为一大妙计。…...

C++继承与派生
1.基本知识 类的继承是新类从已有类那里获得特性,从已有的类产生新类的过程称为类的派生; 已有类称为基类或父类,派生出的新类则称为派生类或子类; 继承的功能: (1)使得基类与派生类之间建立…...

Survival Animations
一套生存游戏的动画集,包括采集、建造、捕鱼、剥皮/鞣制、篝火等更多内容。 总动画数:89 建造/制作 30 篝火 28 饮水 3 水壶 3 觅食 2 治疗 3 空闲 1 原始捕鱼 7 剥皮 1 矛捕鱼 4 伐木 5 下载:Unity资源商店链接资源下载链接 效果图:...

Cargo 教程
Cargo 教程 1. 引言 Cargo 是 Rust 编程语言的包管理器和构建工具。它为 Rust 项目提供了依赖管理、编译和打包等功能。本教程将详细介绍 Cargo 的基本用法,帮助您快速上手 Rust 项目开发。 2. 安装 Cargo 在开始使用 Cargo 之前,您需要确保已经安装了 Rust 编程语言。Ru…...
linux中“PXE高效批量装机”
在大规模的 Linux 应用环境中,如 Web 群集、分布式计算等,服务器往往并不配备光驱设备,在这种情况下,如何为数十乃至上百台服务器裸机快速安装系统呢?传统的 USB光驱、移动硬盘等安装方法显然已经难以满足需求。 PXE …...
emm, ComfyUI的作者从Stability.AI离职了
🍖背景 今天在更新ComfyUI的过程中,看到Manager中有这样一段描述: 嗯?做了新的官方网站?然后开始新篇章? 难道说ComfyUI的作者从Stability.AI离职了? 赶紧点开链接看了下,emm&…...
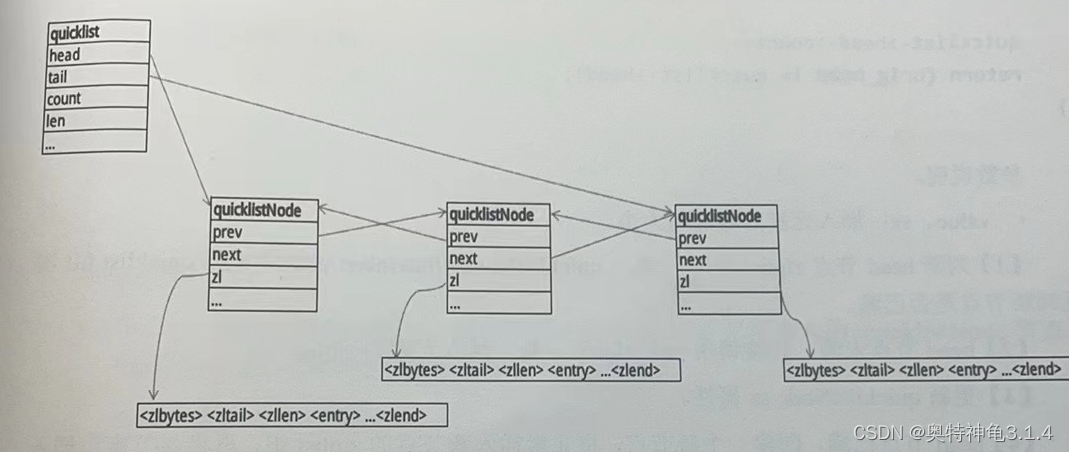
Redis-五种数据结构之列表(ziplist、quicklist)
列表 文章目录 列表压缩列表-ziplistziplist 定义级联更新 快速列表-quicklistquicklistNode 定义quicklist 定义quicklist常用操作其他操作quicklist 相对于普通链表优点quick应用场景在redis 中使用quicklist 列表数据类型可以存储一组按插入顺序排序的字符串,他很…...
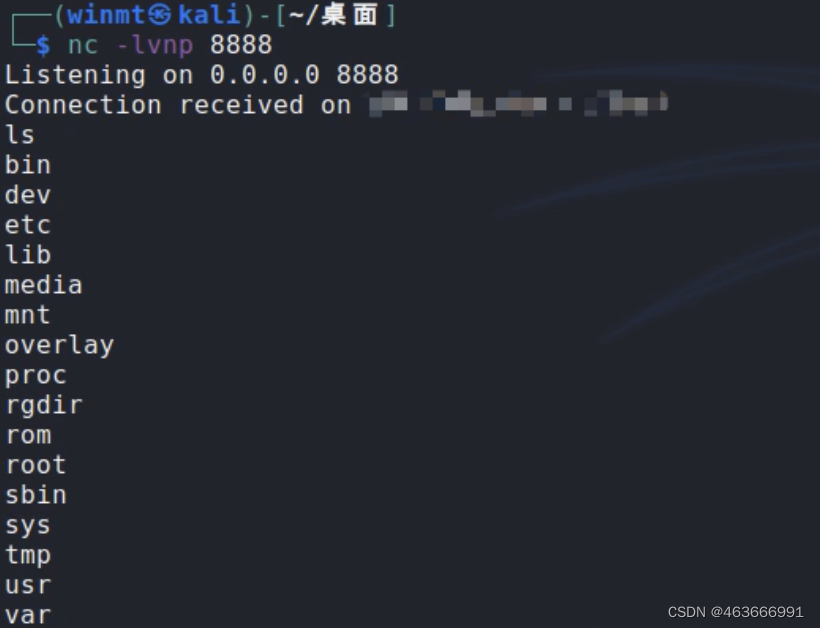
记一次全设备通杀未授权RCE的挖掘经历
想来上一次挖洞还在一年前的大一下,然后就一直在忙活写论文,感觉挺枯燥的(可能是自己不太适合弄学术吧QAQ),所以年初1~2月的时候,有空的时候就又会挖一挖国内外各大知名厂商的设备,拿了几份思科…...

【数据库编程-SQLite3(一)】sqlite3数据库在Windows下的配置及测试
学习分析 1、资源准备2、环境配置2.1、将资源包下载解压缩保存。2.2、在QT中创建工程,配置环境 3、测试配置3.1、 sqlite3_open函数3.2、sqlite3_close函数3.3、代码测试 1、资源准备 资源包 2、环境配置 2.1、将资源包下载解压缩保存。 解压缩得到以下文件 2.2、在QT中创建…...

YOLOv10改进 | 主干篇 | YOLOv10引入华为VanillaNet替换Backbone
1. VanillaNet介绍 1.1 摘要: 基础模型的核心是“越多越好”的理念,计算机视觉和自然语言处理领域取得的惊人成功就是例证。 然而,优化的挑战和变压器模型固有的复杂性要求范式向简单性转变。 在这项研究中,我们介绍了 VanillaNet,一种设计优雅的神经网络架构。 通过避免…...

C++ 迷宫问题
描述 定义一个二维数组 N*M ,如 5 5 数组下所示: int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走…...

【Linux】Linux文件系统中主要文件夹列举_作用说明
在Linux系统中,文件夹(或称为目录)的组织结构是系统功能和用户数据的重要组成部分。以下是Linux系统中一些主要文件夹的列举及其作用说明: / (根目录): 是Linux文件系统的起点。通常只包含其他目录,不建议直接在其中存…...

移植案例与原理 - HDF驱动框架-驱动配置(1)
HCS(HDF Configuration Source)是HDF驱动框架的配置描述源码,内容以Key-Value为主要形式。它实现了配置代码与驱动代码解耦,便于开发者进行配置管理。应该,类似Linux DTS(Device Tree Source)设备树。 HC-GEN(HDF Configuration Generator)是…...
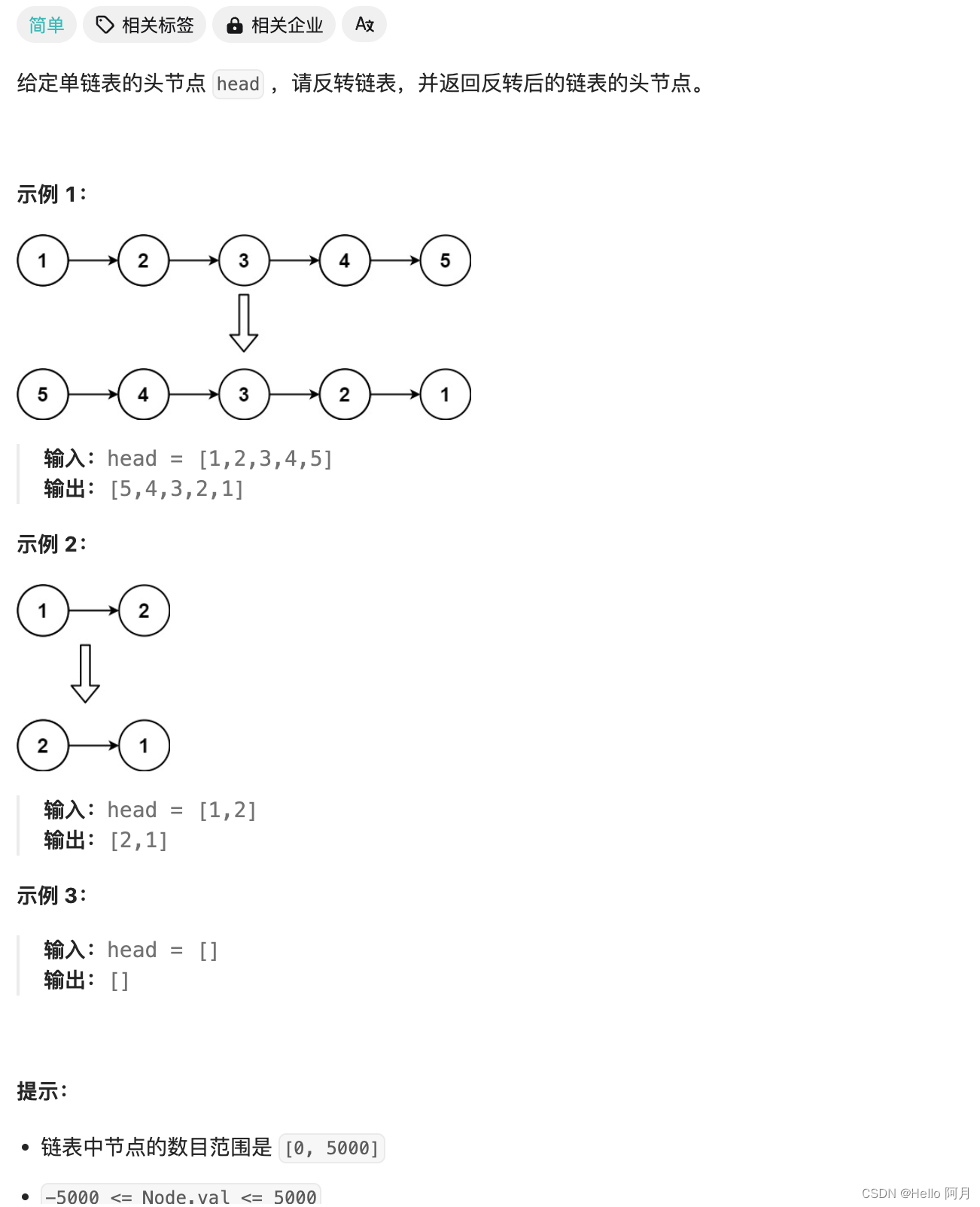
坚持刷题|反转链表
文章目录 题目思考实现1. 迭代方式实现链表翻转2. 递归方式实现链表翻转 Hello,大家好,我是阿月。坚持刷题,老年痴呆追不上我,今天继续链表:反转链表 题目 LCR 024. 反转链表 思考 翻转链表是一个常见的算法问题&a…...
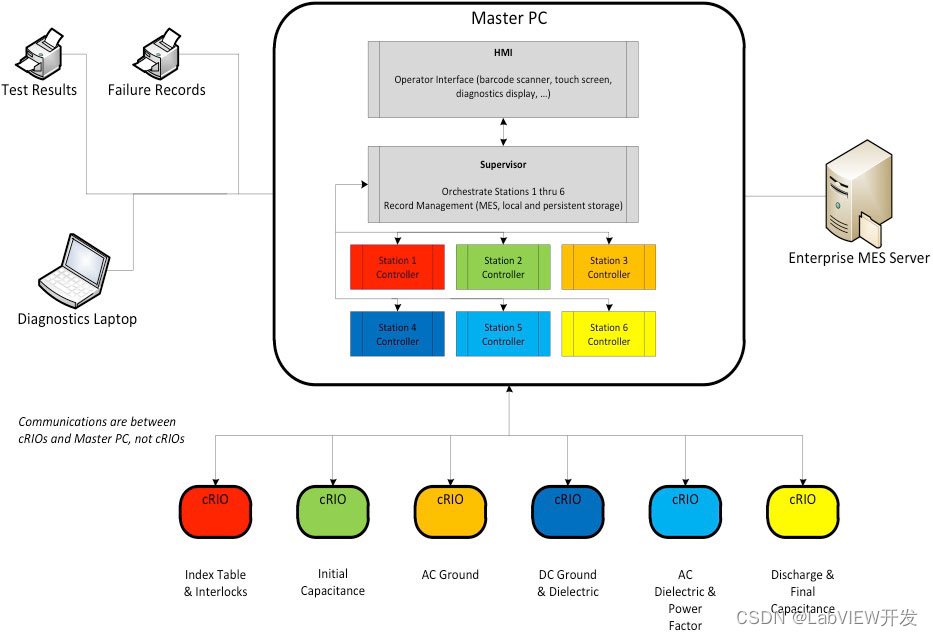
升级和维护老旧LabVIEW程序
在升级老旧LabVIEW程序至64位环境时,需要解决兼容性、性能和稳定性等问题。本文从软件升级、硬件兼容性、程序优化、故障修复等多个角度详细分析。具体包括64位迁移注意事项、修复页面跳转崩溃、解决关闭程序后残留进程的问题,确保程序在新环境中的平稳运…...

sqlite数据库整体迁移进mysql整个流程并解决中文异常问题
咨询【QQ】 sqlite轻量数据还行,随着数据量增大,不得不迁移进mysql 首先 电脑执行 sqlite3 db.sqlite3 .dump > dump.sql 会把整个sqlite的数据导出进 dump.sql中 紧接着我们把sqlite的sql转换成mysql的sql语句,因为mysql语句和 sq…...

Hadoop3:MapReduce中的Partition原理及自定义Partition
一、默认Partition分区配置 以WC案例来进行验证。 1、设置setNumReduceTasks 修改的代码 这行代码,确定了reduceTask的数量,也确定了分区逻辑 在mapper文件中,打上断点 计算分区的代码 这里会对每一个kv进行计算,然后&#…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
