算法 |数字计数
给出n个数字,请你求出在给出的这n个数字当中,最大的数字与次大的数字之差,最大的数字与次小的数字之差,次大的数字与次小的数字之差,次大的数字与最小的数字之差.
易错点
1 1 2 3 4 4
次小不是a[1]了
次大也不是a[n-2]了

#include<bits/stdc++.h>
using namespace std;
int a[110] = {};
int main(){int n;cin>>n;for(int i = 0; i < n; i++)cin>>a[i];sort(a,a+n);int amax1,amin1,amax2,amin2;amax1 = a[n-1];amax2 = a[n-1];amin1 = a[0];amin2 = a[0];for(int i = n-2; i >= 0; i--){if(a[i] != amax2){amax2 = a[i];break;}}for(int i = 1; i <= n - 1; i++){if(a[i] != amin2){amin2 = a[i];break;}}cout<<amax1 - amax2<<" "<<amax1 - amin2<<" ";cout<<amax2 - amin2<<" "<<amax2 - amin1<<endl;return 0;
}
相关文章:

算法 |数字计数
给出n个数字,请你求出在给出的这n个数字当中,最大的数字与次大的数字之差,最大的数字与次小的数字之差,次大的数字与次小的数字之差,次大的数字与最小的数字之差. 易错点 1 1 2 3 4 4 次小不是a[1]了 次大也不是a[n-2]了 #include<bits/stdc.h> using namespace std; …...
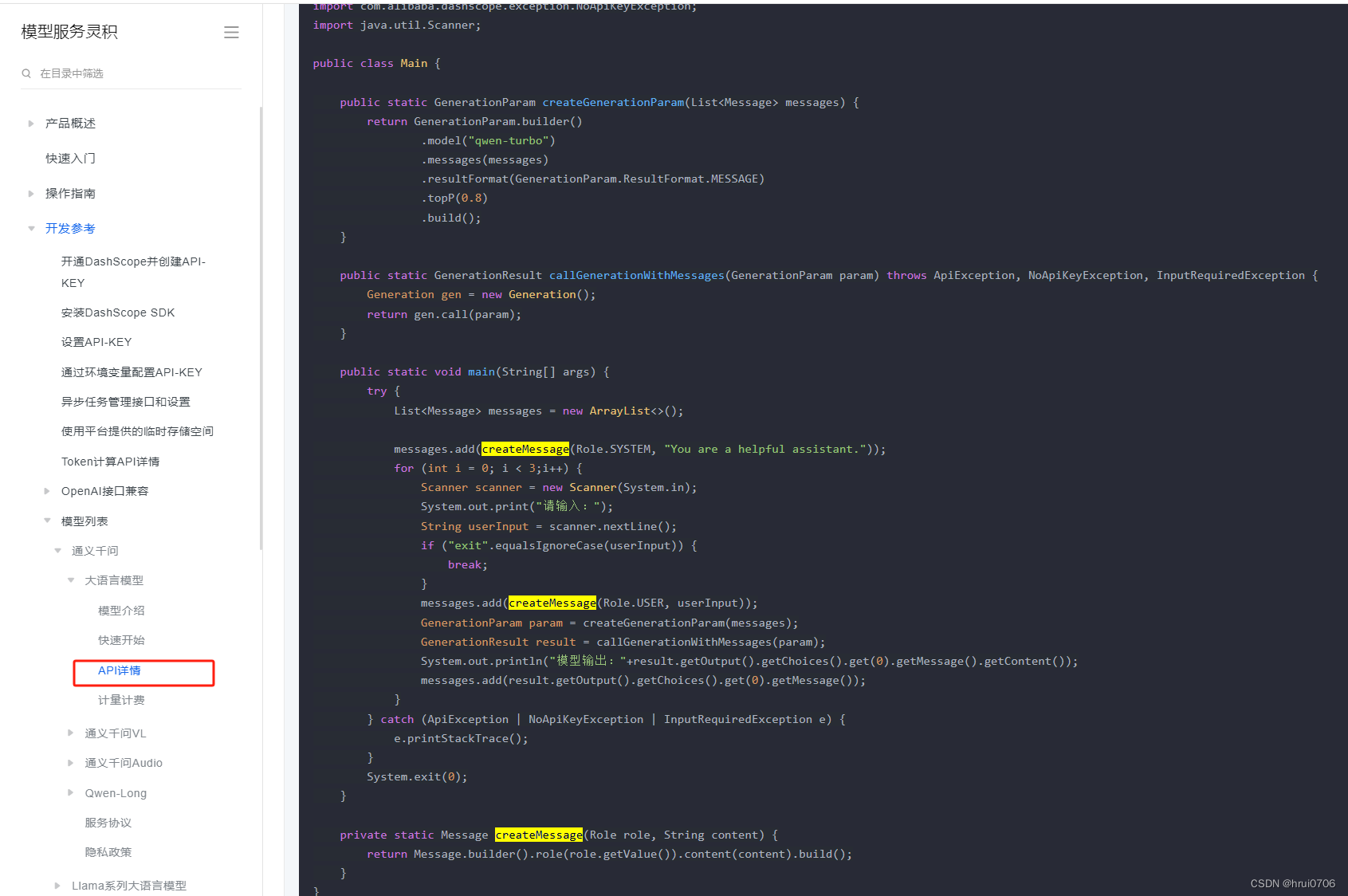
通义千问调用笔记
如何使用通义千问API_模型服务灵积(DashScope)-阿里云帮助中心 package com.ruoyi.webapp.utils;import com.alibaba.dashscope.aigc.generation.Generation; import com.alibaba.dashscope.aigc.generation.GenerationOutput; import com.alibaba.dashscope.aigc.generation.G…...

Linux常见的压缩文件种类与对应的压缩解压方法
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

LNMP网站架构
一、安装nginx服务 1、关闭防火墙和核心防护 systemctl stop firewalld systemctl disable firewalld setenforce 0 2、安装依赖包 yum -y install pcre-devel zlib-devel openssl-devel gcc gcc-c make 3、创建运行用户 useradd -M -s /sbin/nologin nginx 4、编译安装…...
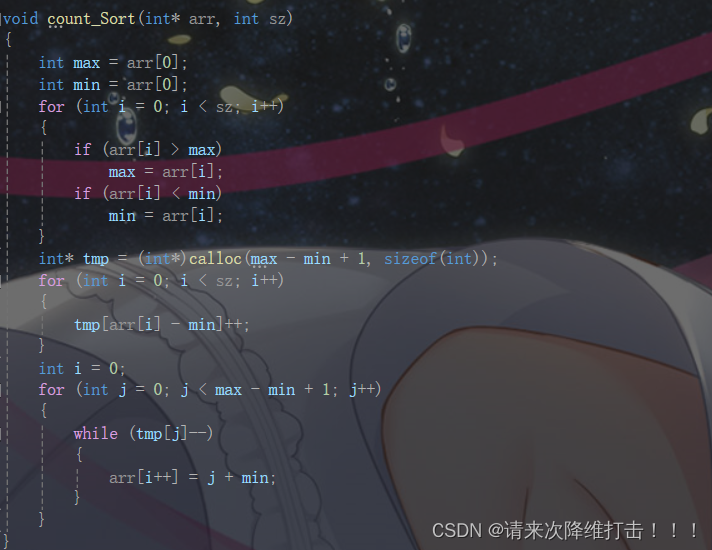
排序算法及源代码
堆排序: 在学习堆之后我们知道了大堆和小堆,对于大堆而言第一个节点就是对大值,对于小堆而言,第一个值就是最小的值。如果我们把第一个值与最后一个值交换再对最后一个值前面的数据重新建堆,如此下去就可以实现建堆排…...

力扣第206题“反转链表”
在本篇文章中,我们将详细解读力扣第206题“反转链表”。通过学习本篇文章,读者将掌握如何使用迭代和递归的方法来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第…...
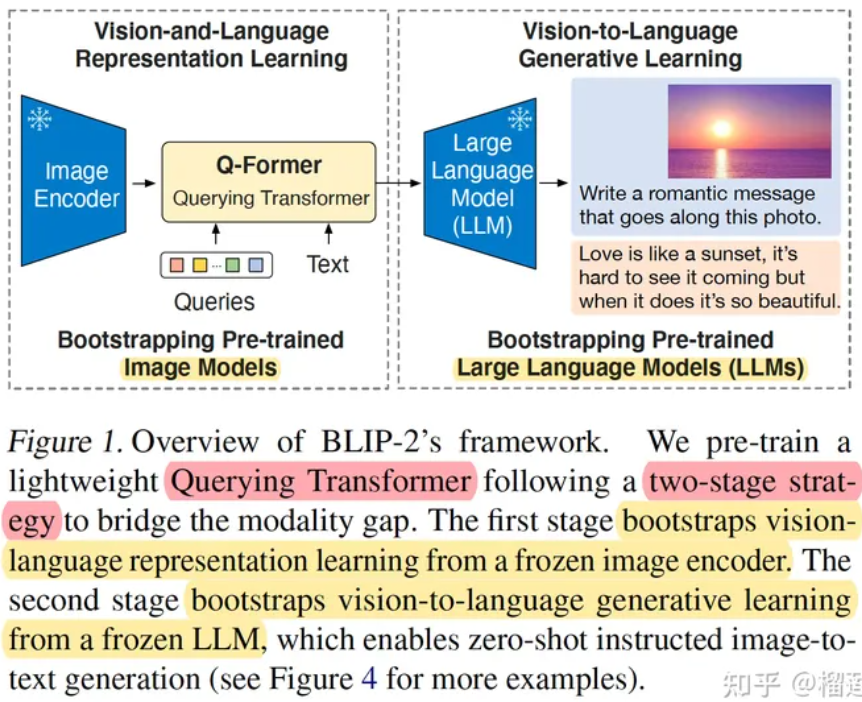
多模态大模型解读
目录 1. CLIP 2. ALBEF 3. BLIP 4. BLIP2 参考文献 (2023年)视觉语言的多模态大模型的目前主流方法是:借助预训练好的LLM和图像编码器,用一个图文特征对齐模块来连接,从而让语言模型理解图像特征并进行深层次的问…...

React是什么?
theme: condensed-night-purple highlight: atelier-cave-light React是什么? 官方的解释是:A JavaScript library for building user interfaces用于构建用户界面的 JavaScript 库 那为什么要选择用React呢? 原生的HTML、CSS、JavaScrip的…...

创新入门 | 病毒循环Viral Loop是什么?为何能实现指数增长
今天,很多高速增长的成功创业公司都在采用”病毒循环“的策略去快速传播、并扩大用户基础。究竟什么是“病毒循环”?初创公司的创始人为何需要重视这个策略?这篇文章中将会一一解答与病毒循环有关的各种问题。 一、什么是病毒循环(…...

鸿蒙HarmonyOS实战:渲染控制、路由案例
条件渲染 简单来说,就是动态控制组件的显示与隐藏,类似于vue中的v-if 但是这里写法就是用if、else、else if看起来更像是原生的感觉 效果 循环渲染 我们实际开发中,数据一般是后端返回来的对象格式,对此我们需要进行遍历&#…...
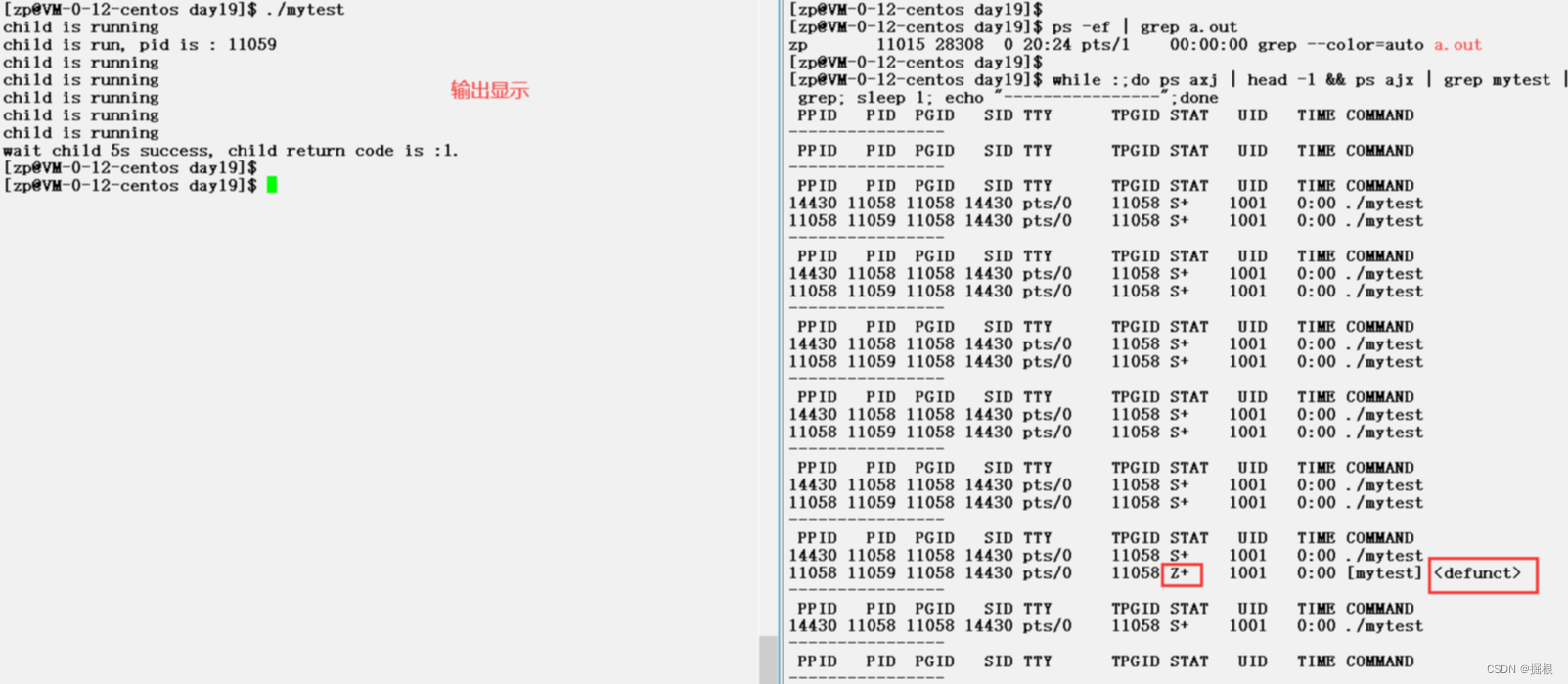
【Linux】进程控制2——进程等待(waitwaitpid)
1. 进程等待必要性 我们知道,子进程退出,父进程如果不管不顾,就可能造成"僵尸进程”的问题,进而造成内存泄漏。另外,进程一旦变成僵尸状态,那就刀枪不入,“杀人不眨眼”的kill -9 也无能为…...

SpringBoot 统计接口调用耗时的多种方式
在实际开发中,了解项目中接口的响应时间是必不可少的事情。SpringBoot 项目支持监听接口的功能也不止一个,接下来我们分别以 AOP、ApplicationListener、Tomcat 三个方面去实现三种不同的监听接口响应时间的操作。 AOP 首先我们在项目中创建一个类 &am…...
Linux系统安装Ruby语言
Ruby是一种面向对象的脚本语言,由日本的计算机科学家松本行弘设计并开发,Ruby的设计哲学强调程序员的幸福感,致力于简化编程的复杂性,并提供一种既强大又易于使用的工具。其语法简洁优雅,易于阅读和书写,使…...

网络安全练气篇——OWASP TOP 10
1、什么是OWASP? OWASP(开放式Web应用程序安全项目)是一个开放的社区,由非营利组织 OWASP基金会支持的项目。对所有致力于改进应用程序安全的人士开放,旨在提高对应用程序安全性的认识。 其最具权威的就是“10项最严重…...

python实现进度条的方法和实现代码
在Python中,有多种方式可以实现进度条。这里,我将介绍七种常见的方法:使用tqdm(这是一个外部库,非常流行且易于使用)、rich、click、progressbar2等库以及纯Python的print函数与time库来模拟进度条。 目录…...

被拷打已老实!面试官问我 #{} 和 ${} 的区别是什么?
引言:在使用 MyBatis 进行数据库操作时,#{} 和 ${} 的区别是面试中常见的问题,对理解如何在 MyBatis 中安全有效地处理 SQL 语句至关重要。正确使用这两种占位符不仅影响应用的安全性,还涉及到性能优化。 题目 被拷打已老实&…...

C# —— while循环语句
作用 让顺序执行的代码 可以停下来 循环执行某一代码块 // 条件分支语句: 让代码产生分支 进行执行 // 循环语句 : 让代码可以重复执行 语法 while循环 while (bool值) { 循环体(条件满足时执行的代码块) …...

力扣第205题“同构字符串”
在本篇文章中,我们将详细解读力扣第205题“同构字符串”。通过学习本篇文章,读者将掌握如何使用哈希表来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第205题“…...

探索RESTful API开发,构建可扩展的Web服务
介绍 当我们浏览网页、使用手机应用或与各种互联网服务交互时,我们经常听到一个术语:“RESTful API”。它听起来很高深,但实际上,它是构建现代网络应用程序所不可或缺的基础。 什么是RESTful API? 让我们将RESTful …...

苹果安卓网页的H5封装成App的应用和原生开发的应用有什么不一样?
H5封装类成App的应用和原生应用有什么不一样?——一对比谈优缺点 1. 开发速度和复用性 H5封装的App优势:一次编写,多平台运行。你只需要使用一种语言编写代码,就可以发布到不同的平台,降低开发成本。 原生应用优势&…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
