排序题目:有序数组的平方
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:有序数组的平方
出处:977. 有序数组的平方
难度
2 级
题目描述
要求
给定按非递减顺序排序的整数数组 nums \texttt{nums} nums,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。
示例
示例 1:
输入: nums = [-4,-1,0,3,10] \texttt{nums = [-4,-1,0,3,10]} nums = [-4,-1,0,3,10]
输出: [0,1,9,16,100] \texttt{[0,1,9,16,100]} [0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100] \texttt{[16,1,0,9,100]} [16,1,0,9,100]。排序后,数组变为 [0,1,9,16,100] \texttt{[0,1,9,16,100]} [0,1,9,16,100]。
示例 2:
输入: nums = [-7,-3,2,3,11] \texttt{nums = [-7,-3,2,3,11]} nums = [-7,-3,2,3,11]
输出: [4,9,9,49,121] \texttt{[4,9,9,49,121]} [4,9,9,49,121]
数据范围
- 1 ≤ nums.length ≤ 10 4 \texttt{1} \le \texttt{nums.length} \le \texttt{10}^\texttt{4} 1≤nums.length≤104
- -10 4 ≤ nums[i] ≤ 10 4 \texttt{-10}^\texttt{4} \le \texttt{nums[i]} \le \texttt{10}^\texttt{4} -104≤nums[i]≤104
- nums \texttt{nums} nums 已按非递减顺序排序
进阶
计算每个元素的平方并对新数组排序的解法很简单,你可以使用不同的方法找到时间复杂度 O(n) \texttt{O(n)} O(n) 的解法吗?
解法一
思路和算法
最直观的解法是依次计算数组 nums \textit{nums} nums 中的每个元素的平方并存入新数组中,然后对新数组按非递减顺序排序,即可得到排序后的新数组。
代码
class Solution {public int[] sortedSquares(int[] nums) {int length = nums.length;int[] squares = new int[length];for (int i = 0; i < length; i++) {squares[i] = nums[i] * nums[i];}Arrays.sort(squares);return squares;}
}
复杂度分析
-
时间复杂度: O ( n log n ) O(n \log n) O(nlogn),其中 n n n 是数组 nums \textit{nums} nums 的长度。计算数组 nums \textit{nums} nums 中的每个元素的平方并存入新数组需要 O ( n ) O(n) O(n) 的时间,对新数组排序需要 O ( n log n ) O(n \log n) O(nlogn) 的时间,因此时间复杂度是 O ( n log n ) O(n \log n) O(nlogn)。
-
空间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 nums \textit{nums} nums 的长度。对新数组排序需要 O ( log n ) O(\log n) O(logn) 的递归调用栈空间。注意返回值不计入空间复杂度。
解法二
思路和算法
解法一没有利用到数组 nums \textit{nums} nums 已经按非递减顺序排序的条件,因此需要对新数组排序,时间复杂度是 O ( n log n ) O(n \log n) O(nlogn)。如果利用数组 nums \textit{nums} nums 已经按非递减顺序排序的条件,则不需要对新数组排序,将时间复杂度降低到 O ( n ) O(n) O(n)。
由于一个数的平方大小与这个数的绝对值有关,因此考虑数组 nums \textit{nums} nums 中的绝对值最大元素与绝对值最小元素可能出现的位置。
数组 nums \textit{nums} nums 按非递减顺序排序,可能有以下三种情况:
-
数组 nums \textit{nums} nums 的所有元素都是非负数,元素顺序为绝对值非递减顺序,首个元素的绝对值最小,末尾元素的绝对值最大;
-
数组 nums \textit{nums} nums 的所有元素都是非正数,元素顺序为绝对值非递增顺序,首个元素的绝对值最大,末尾元素的绝对值最小;
-
数组 nums \textit{nums} nums 中既有正数也有负数,首个元素或末尾元素的绝对值最大。
对于上述三种情况中的任意一种情况,绝对值最大的元素一定是数组 nums \textit{nums} nums 的首个元素或末尾元素。因此可以从数组 nums \textit{nums} nums 的两端向中间遍历,按照绝对值从大到小的顺序依次遍历数组 nums \textit{nums} nums 的元素,计算每个元素的平方,反向填入新数组。
具体做法是,维护两个下标 index 1 \textit{index}_1 index1 和 index 2 \textit{index}_2 index2,初始时 index 1 \textit{index}_1 index1 指向数组 nums \textit{nums} nums 的首个元素, index 2 \textit{index}_2 index2 指向数组 nums \textit{nums} nums 的末尾元素。遍历过程中,比较 nums [ index 1 ] \textit{nums}[\textit{index}_1] nums[index1] 和 nums [ index 2 ] \textit{nums}[\textit{index}_2] nums[index2] 这两个元素的绝对值:
-
如果 nums [ index 1 ] \textit{nums}[\textit{index}_1] nums[index1] 的绝对值大于 nums [ index 2 ] \textit{nums}[\textit{index}_2] nums[index2] 的绝对值,则将 nums [ index 1 ] \textit{nums}[\textit{index}_1] nums[index1] 的平方填入新数组,将 index 1 \textit{index}_1 index1 加 1 1 1;
-
如果 nums [ index 1 ] \textit{nums}[\textit{index}_1] nums[index1] 的绝对值小于等于 nums [ index 2 ] \textit{nums}[\textit{index}_2] nums[index2] 的绝对值,则将 nums [ index 2 ] \textit{nums}[\textit{index}_2] nums[index2] 的平方填入新数组,将 index 2 \textit{index}_2 index2 减 1 1 1。
由于遍历数组 nums \textit{nums} nums 的过程中,每次遍历的元素都是尚未遍历的元素中的绝对值最大的元素,因此遍历元素的顺序是绝对值非递增顺序,即元素的平方非递增顺序。将遍历的元素的平方反向填入新数组,新数组中的元素顺序为非递减顺序。
代码
class Solution {public int[] sortedSquares(int[] nums) {int length = nums.length;int[] squares = new int[length];int index1 = 0, index2 = length - 1;for (int i = length - 1; i >= 0; i--) {if (Math.abs(nums[index1]) > Math.abs(nums[index2])) {squares[i] = nums[index1] * nums[index1];index1++;} else {squares[i] = nums[index2] * nums[index2];index2--;}}return squares;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度。需要遍历数组 nums \textit{nums} nums 中的每个元素一次。
-
空间复杂度: O ( 1 ) O(1) O(1)。注意返回值不计入空间复杂度。
相关文章:

排序题目:有序数组的平方
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:有序数组的平方 出处:977. 有序数组的平方 难度 2 级 题目描述 要求 给定按非递减顺序排序的整…...

PPT可以转换成Word吗?归纳了三种转换方式
PPT可以转换成Word吗?在当今快节奏的工作和学习环境中,不同格式文件之间的转换变得日益重要。PPT作为演示文稿制作的首选工具,广泛应用于会议演讲、教育培训等多个场景,而Word则是文档编辑与编排的基石。为了便于进一步编辑、分享…...
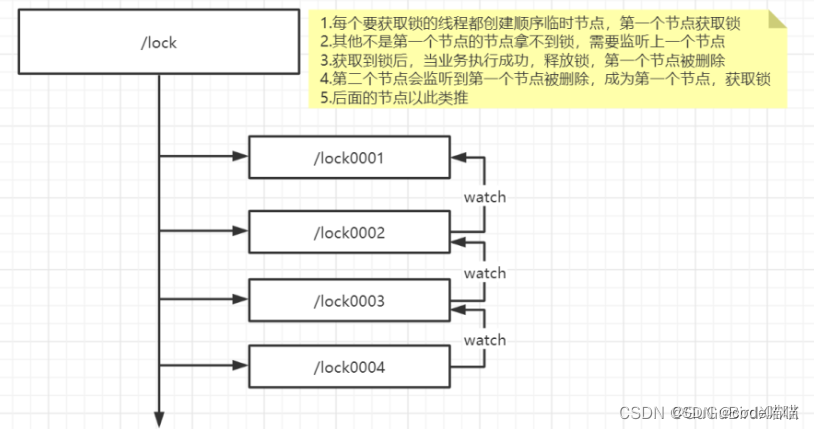
分布式锁三种方案
基于数据库的分布式锁(基于主键id和唯一索引) 1基于主键实现分布式锁 2基于唯一索引实现分布式锁 其实原理一致,都是采用一个唯一的标识进行判断是否加锁。 原理:通过主键或者唯一索性两者都是唯一的特性,如果多个…...

【HarmonyOS NEXT】har 包的构建生成过程
Har模块文件结构 构建HAR 打包规则 开源HAR除了默认不需要打包的文件(build、node_modules、oh_modules、.cxx、.previewer、.hvigor、.gitignore、.ohpmignore)和.gitignore/.ohpmignore中配置的文件,cpp工程的CMakeLists.txt,…...
)
从0开发一个Chrome插件:项目实战——翻译插件(附带申请谷歌翻译、百度翻译教程)
前言 这是《从0开发一个Chrome插件》系列的第十八篇文章,本系列教你如何从0去开发一个Chrome插件,每篇文章都会好好打磨,写清楚我在开发过程遇到的问题,还有开发经验和技巧。 专栏: 从0开发一个Chrome插件:什么是Chrome插件?从0开发一个Chrome插件:开发Chrome插件的必…...

查看nginx安装/配置路径,一个服务器启动两个nginx
查看nginx安装/配置路径 查看nginx的pid: ps -ef | grep nginx查看pid对应服务的启动路径 ll /proc/2320/exe使用检查配置文件命令,查看配置文件位置 /usr/local/nginx/sbin/nginx -t一个服务启动两个nginx 拷贝一份程序,cpbin是我自己创…...

JavaScript中 Map与reduce的应用
1. Map:映射新世界 Map构造函数创建一个新Map对象,它允许你以键值对的形式存储数据,提供了一种更加灵活的数据结构。与传统的对象相比,Map允许任何值(包括对象)作为键,而且具有更好的性能表现。…...

1688商品详情API:一键解锁海量批发数据
引言 1688作为阿里巴巴旗下的B2B交易平台,拥有庞大的商品数据库和丰富的供应商资源。对于想要获取商品详细信息的开发者和企业而言,1688提供的API接口是获取一手数据的关键途径。本文将详细介绍如何使用1688商品详情API,包括注册、获取API密…...
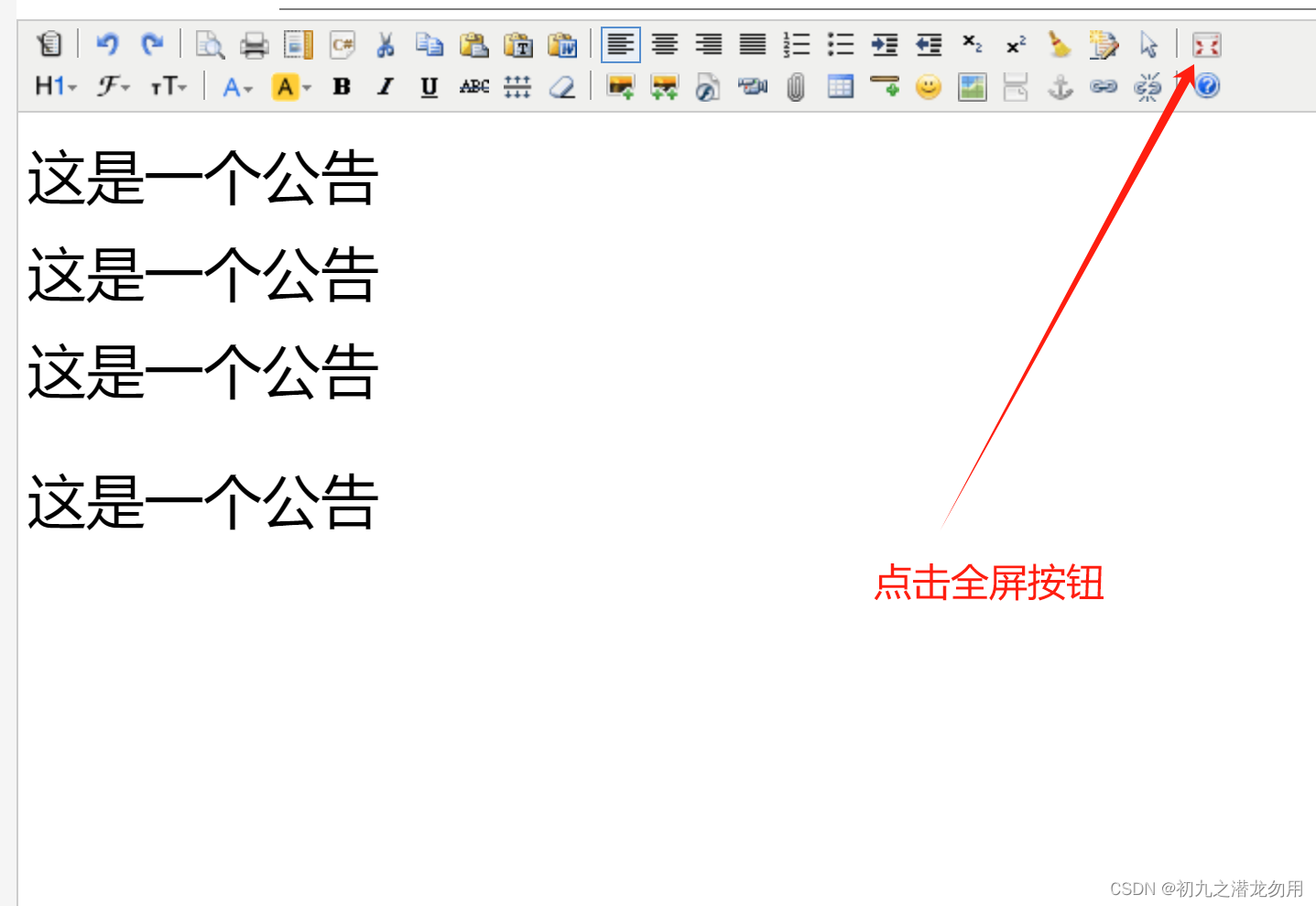
C#结合JS 修改解决 KindEditor 弹出层问题
目录 问题现象 原因分析 范例运行环境 解决问题 修改 kindeditor.js C# 服务端更新 小结 问题现象 KindEditor 是一款出色的富文本HTML在线编辑器,关于编辑器的详细介绍可参考我的文章《C# 将 TextBox 绑定为 KindEditor 富文本》,这里我们讲述在…...
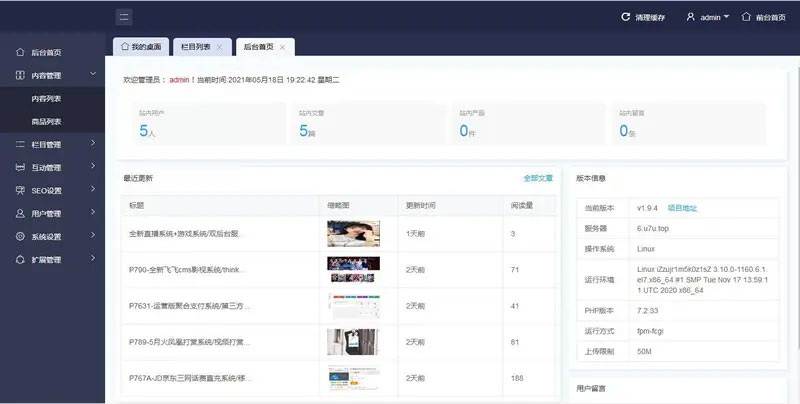
二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面
二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面 二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面...
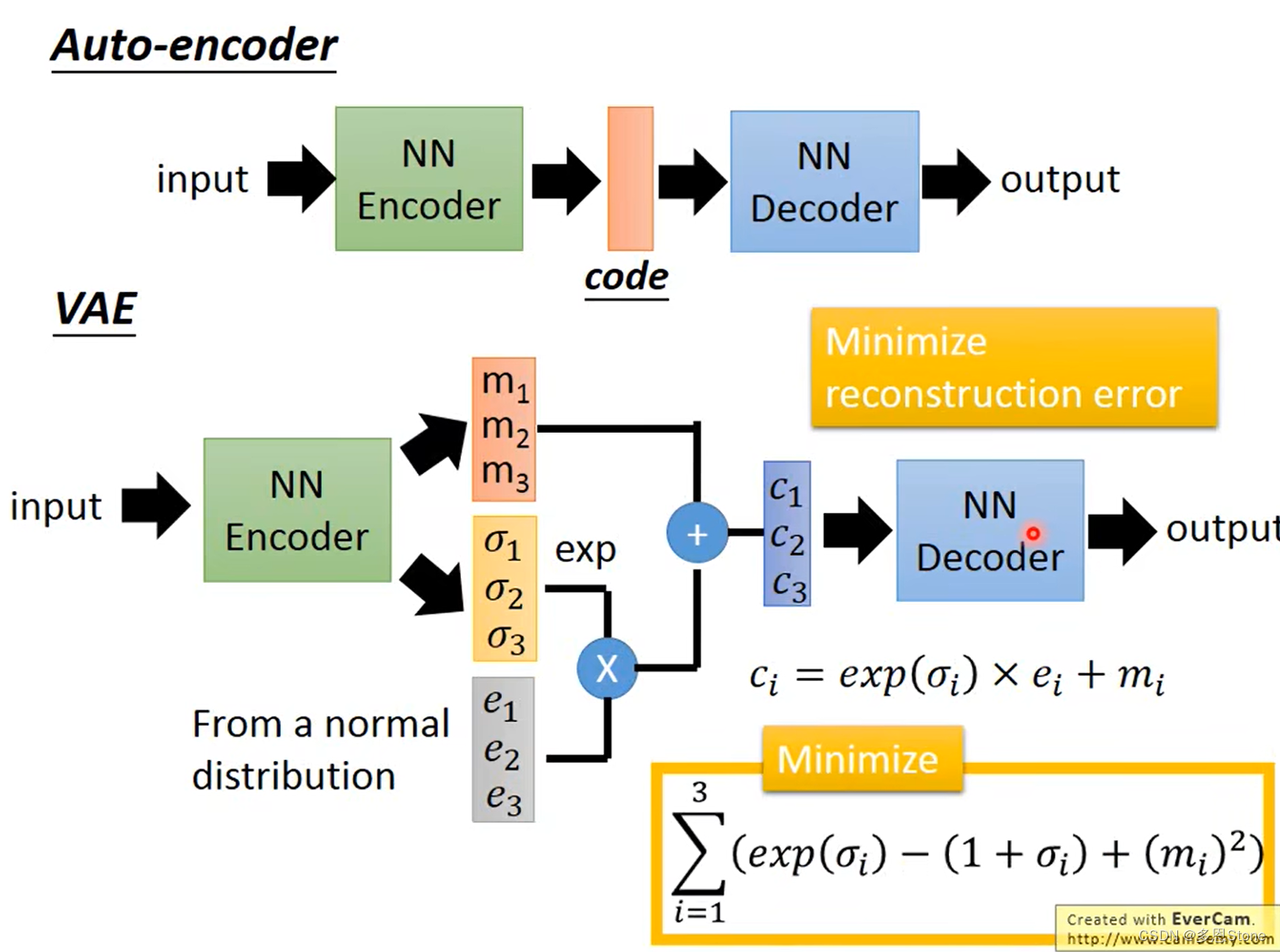
【diffusers极速入门(三)】生成的图像尺寸与 UNet 和 VAE 之间的关系
先上结论,一句话总结即: SD 图片的输入\输出尺寸(高或宽) Unet 输入\输出的样本尺寸(高或宽) x VAE 的缩放尺寸 在使用生成模型时,特别是图像生成任务中,理解 UNet 和 VAE…...

react实现窗口悬浮框,可拖拽、折叠、滚动
1、效果如下 2、如下两个文件不需要修改 drag.js import React from "react"; import PropTypes from "prop-types";export default class DragM extends React.Component {static propTypes {children: PropTypes.element.isRequired};static defaultP…...

52【场景作图】空间感
参考 场景绘制,画面空间感如何拉开?分分钟就能学会的场景优化思路更新啦!_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1pa411J7Ps/?spm_id_from333.337.search-card.all.click&vd_source20db0c4e2d303527ed13c4b9cdf698ec 1 …...
SpringBoot系列之搭建WebSocket应用
SpringBoot系列之ServerEndpoint方式开发WebSocket应用。在实时的数据推送方面,经常会使用WebSocket或者MQTT来实现,WebSocket是一种不错的方案,只需要建立连接,服务端和客户端就可以进行双向的数据通信。很多网站的客户聊天&…...
RK3568技术笔记十四 Ubuntu创建共享文件夹
单击“虚拟机”,单击“设置”,如图所示: 单击“选项”,选择“总是启用(E)”,单击“添加”,如图所示: 单击“下一步”,如图所示: 单击“浏览”添加…...

JavaScript 获取地理位置 Geolocation
在现代的 web 应用程序中,获取用户的地理位置信息是一项常见的需求。这可以用于提供个性化内容、本地化服务或者基于位置的功能。HTML5 引入了 Geolocation API,使得从浏览器中获取地理位置信息变得非常简单。 1. Geolocation API 简介 Geolocation AP…...
android串口助手apk下载 源码 演示 支持android 4-14及以上
android串口助手apk下载 1、自动获取串口列表 2、打开串口就开始接收 3、收发 字符或16进制 4、默认发送at\r\n 5、android串口助手apk 支持android 4-14 (Google seral port 太老) 源码找我 需要 用adb root 再setenforce 0进入SELinux 模式 才有权限…...

windows11 生产力工具配置
一、系统安装 官方windows11.iso镜像文件安装操作系统时,会强制要求联网验证,否则无法继续安装操作系统,跳过联网登录账号的方式为:按下【shiftF10】快捷键,调出cmd命令窗口,输入命令 OOBE\BYPASSNRO 等…...

Nacos配置中心不可用会有什么影响
服务端: Nacos的数据存储接口 com.alibaba.nacos.config.server.service.DataSourceService 有两种实现: 如果指定了mysq 作为数据库,则必须使用 mysql 如果是 集群方式部署Nacos,则必须使用mysql 如果是单例方式部署 并且 没…...
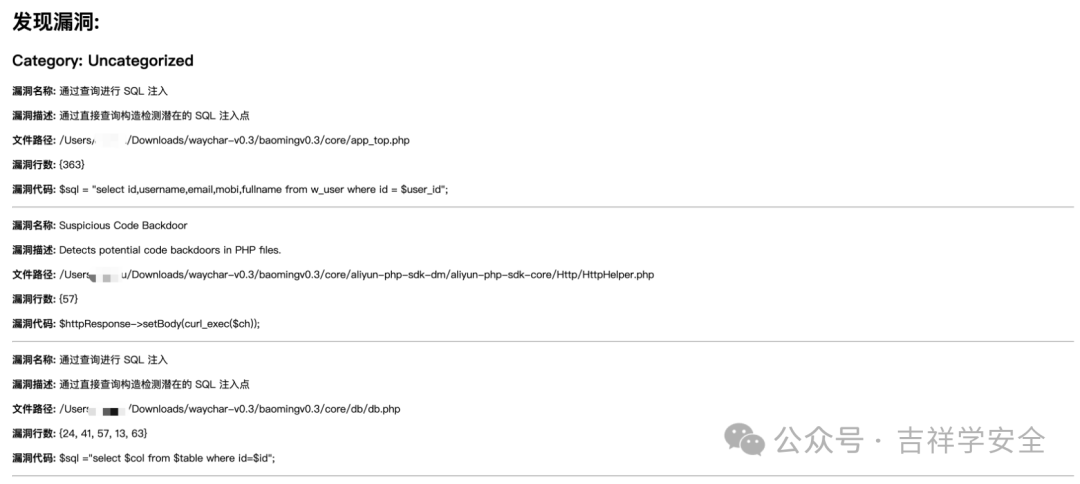
AI时代下的自动化代码审计工具
代码审计工具分享 吉祥学安全知识星球🔗除了包含技术干货:Java代码审计、web安全、应急响应等,还包含了安全中常见的售前护网案例、售前方案、ppt等,同时也有面向学生的网络安全面试、护网面试等。 这两年一直都在提“安全左移”&…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
