秋招突击——6/16——复习{(单调队列优化DP)——最大子序和,背包模型——宠物小精灵收服问题}——新作{二叉树的后序遍历}
文章目录
- 引言
- 复习
- (单调队列优化DP)——最大子序和
- 单调队列的基本实现思路——求可移动窗口中的最值
- 总结
- 背包模型——宠物小精灵收服问题
- 思路分析
- 参考思路分析
- 新作
- 二叉树的后续遍历加指针调换
- 总结
引言
复习
(单调队列优化DP)——最大子序和
- 这个已经是第二天做了,昨天基本上已经做了很多推理,今天就要把这道题完成,下述是昨天的学习的链接
- 单调递增队列的推理
- 昨天经过推理,知道了要将这个问题进行转换,由原先的特定长度和的最大值,转成求特定长度和的最小值。然后通过画图证明了,为什么要通过单调队列实现最小值的计算。
- 今天主要是关注代码的执行。
单调队列的基本实现思路——求可移动窗口中的最值
- 使用队列维系一个集合m
- 将无用的元素从后往前进行排除,保证队列是一个单调递增的队列
- 找出最大值或者最小值
在这里的队列保存的元素是的特定序列的累加和,不是具体的元素的大小,保证单调递增!!
- 这个代码不是那么好懂,我自己再写一遍。
#include <iostream>using namespace std;typedef long long LL;
const int N = 300010;
int q[N],s[N];
int n,m;int main(){cin>>n>>m;for (int i = 1; i <= n ; ++i) {cin>>s[i];s[i] += s[i - 1];}// 创建对应的队列int hh = 0,tt = 0,res = INT_MIN;q[hh] = 0;for (int i = 1; i <= n; ++i) {// 保证队列的长度不变if (i - hh > m) hh++;// 计算最值res = max(res , s[i] - s[q[hh]]);// 更新的队列尾部// 队列可为空,也就是tt >= hh// 然后就是保证队列是单调递增的,如果出现新的值小于后续的值,// 就要将所有比之大的数据排除,因为是一个序列,一定会选中这个数据while(tt >= hh && s[q[tt]] > s[i]) tt --;// 移动到一个小于或者等于的数字之后,tt再往后移动一个,即将新的排序值,加入其中。q[++tt] = i; }cout<<res;
}
总结
- 重新写了一遍,效果好多了,并没有像之前那么难以理解了,主要有两个地方需要好好整理一下,分别是
- 这里的单调递增是针对S,也就是每一个前序和来说的,不是针对特定的某一个元素说的。
- 这里使用一个数组模拟队列,hh模拟队列的头指针,tt模拟队列的尾指针
- hh头指针只需要保证是最小值,并且队列的长度不超过m
- tt尾指针需要覆盖新的元素,保证整个队列是单调递增的,因为这是一个序列和,如果后续的序列和比前面的小,那么最终就不一定不会选择前面的序列和。
背包模型——宠物小精灵收服问题

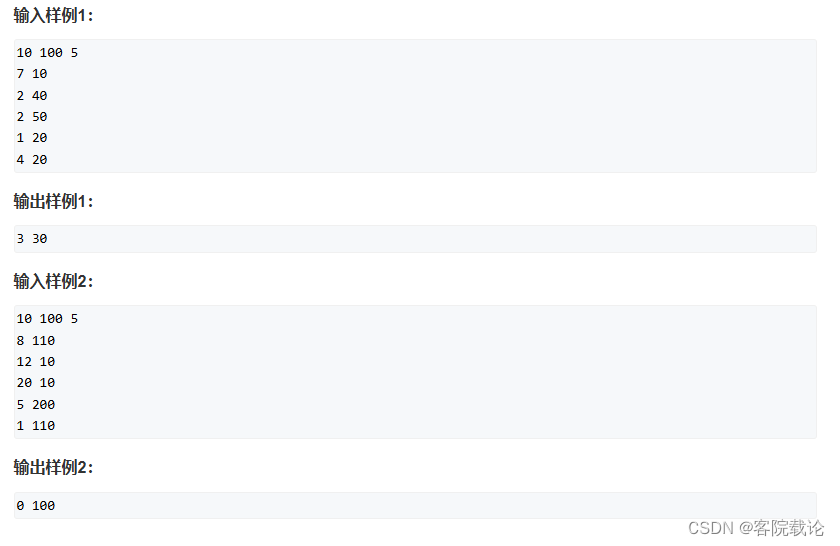
思路分析
-
这道题是经典的背包模型问题,收服的精灵就是要求在特定空间下装的货越多,然后的皮卡丘收到的伤害就是代价越小越好,
-
每一个状态的集合,主要分为两个部分,收取当前的精灵和不收取当前的精灵,而且要同时满足两个约束的,就是最多收服精灵的个数,皮卡丘最少收到的伤害,不过究竟哪个更加重要?明白了,尽可能多的精灵,然后同样多的情况下,保证尽可能多的剩余体力。所以,这里要两个矩阵
- 一个保存数量,这个属性值,也是dp的主要目标
- 另外一个保存剩余的体力值,这个用来后续判断
-
感觉有点不对,这里是不是要再增加一个新的遍历条件,也就是体力值?如果不增加就没有意义了。
-
暂时实现成这样了,还有点问题,不过时间不够了,直接看代码了
#include <iostream>using namespace std;const int N = 1010,M = 505,K = 105; // N是精灵球的数量,M是皮卡丘的体力值,K是野生小精灵的数量
int f[K][N],mr[K][N],n1[K],m1[K];
int n,m,k;
int main(){cin>>n>>m>>k;for (int i = 1; i < k; ++i) {cin>>n1[i]>>m1[i];}// 遍历对应的数据for (int i = 1; i < k; ++i) {for (int j = 0; j < N; ++j) {f[i][j] = 0;// 两种状态,// 一种是收服当前的精灵,f[i-1][j - n1[i]] + 1// 判定当前剩余的体力以及精灵球的数量是否满足要求if (m >= m1[i] && k >= n1[i])f[i][j] = f[i-1][j - n1[i]] + 1;// 另外一种是不收服当前的精灵,f[i-1][j]int temp = f[i-1][j];if (temp > f[i][j]){// 不收服的结果大于当前的结果f[i][j] = temp;}else{m -= m1[i];n -= n1[i];}}}// 输出最终的结果,遍历一下}
参考思路分析
- 这里是二维背包问题,需要考虑两个维度,所以我上面的思路有问题,应该使用二维背包去解决这个问题。
- 这里先直接贴代码,参考分析一下
- 二维背包,然后使用滚动数组进行优化
- 然后遍历最后一个维度下,精灵球最多的情况下,体力值消耗最小的情况。
- 还是得看看之前的背包问题咋写的,一维和二维之间的相互转换。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, M = 1010, K = 510;int n, m, t;
int v1[N], v2[N];
int f[M][K];int main()
{//inputcin >> m >> t >> n;for (int i = 1; i <= n; ++ i) cin >> v1[i] >> v2[i];//dpfor (int i = 1; i <= n; ++ i){for (int j = m; j >= v1[i]; -- j){for (int k = t - 1; k >= v2[i]; -- k){f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);}}}//outputcout << f[m][t - 1] << " ";//找到满足最大价值的所有状态里,第二维费用消耗最少的int cost_health = t;for (int k = 0; k <= t - 1; ++ k){if (f[m][k] == f[m][t - 1]){cost_health = min(cost_health, k);}}cout << t - cost_health << endl;return 0;
}
作者:一只野生彩色铅笔
链接:https://www.acwing.com/solution/content/52741/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
新作
- 今天晚上会进行的某公司的主管面,今天新做的题目就是主管面的手撕算法题。
二叉树的后续遍历加指针调换
- 这道题吃亏在于我没有看清楚题目,没有理解他的题目,我觉得他说的比较混乱,而且有一个东西感觉没有任何意义。
- 不过我也发现我的问题了,二叉树定义哪里有问题,没有实现的好。
- 下面是我写的, 大概是写对的
#include <iostream>
#include <vector>
using namespace std;struct Node{int val;Node* left;Node* right;Node(int x):val(x),left(NULL),right(NULL){};
};vector<int> res;void dfs(Node* root){if (root->left) dfs(root->left);if (root->right) dfs(root->right);res.push_back(root->val);
}int main(){Node* root =new Node(1);dfs(root);for(int i = 0;i < res.size();i ++)cout<<res[i]<<",";delete root;
}
针对第二个问题,表述如下
-
要将二叉树的左右子节点更换为后序遍历中的左右子节点,并且更改之后的结果可能不是一个树,甚至有可能成为其他结构。
-
其实我蛮不能理解他的用意的,究竟是让我干什么?把一个二叉树的左右子节点变为后续遍历顺序中的节点,那么指针的方向有没有改变?然后,构建出来是什么样?原来的结构还要保存吗?
-
如果只是单纯换一个方式,不就是在创建一个后序遍历的链表吗?把每一个节点都加进去不就行了吗?
-
现在还不是很懂这个题目
-
下面是ChatGPT写的,感觉没有什么意义。
#include <iostream>
#include <vector>struct Node {int val;Node* left;Node* right;Node(int x) : val(x), left(nullptr), right(nullptr) {}
};// 后序遍历,记录节点访问顺序
void postOrderDFS(Node* root, std::vector<Node*>& nodes) {if (root == nullptr) {return;}postOrderDFS(root->left, nodes);postOrderDFS(root->right, nodes);nodes.push_back(root);
}// 根据后序遍历的节点顺序调整左右子节点
void adjustNodes(std::vector<Node*>& nodes) {for (size_t i = 0; i < nodes.size() - 1; ++i) {nodes[i]->left = nullptr;nodes[i]->right = nodes[i + 1];}nodes.back()->left = nullptr;nodes.back()->right = nullptr;
}// 辅助函数:中序遍历打印二叉树
void inOrderPrint(Node* root) {if (root == nullptr) {return;}inOrderPrint(root->left);std::cout << root->val << " ";inOrderPrint(root->right);
}// 辅助函数:后序遍历打印二叉树
void postOrderPrint(Node* root) {if (root == nullptr) {return;}postOrderPrint(root->left);postOrderPrint(root->right);std::cout << root->val << " ";
}int main() {// 创建一个简单的二叉树Node* root = new Node(1);root->left = new Node(2);root->right = new Node(3);root->left->left = new Node(4);root->left->right = new Node(5);root->right->left = new Node(6);root->right->right = new Node(7);std::cout << "Original tree (in-order): ";inOrderPrint(root); // 预期输出: 4 2 5 1 6 3 7std::cout << std::endl;std::cout << "Original tree (post-order): ";postOrderPrint(root); // 预期输出: 4 5 2 6 7 3 1std::cout << std::endl;// 后序遍历并记录节点顺序std::vector<Node*> postOrderNodes;postOrderDFS(root, postOrderNodes);// 根据后序遍历顺序调整节点adjustNodes(postOrderNodes);std::cout << "Adjusted structure (in-order): ";inOrderPrint(root); // 可能无法正确打印,因为树结构已改变std::cout << std::endl;std::cout << "Adjusted structure (post-order): ";postOrderPrint(root); // 预期输出与原后序遍历顺序一致std::cout << std::endl;return 0;
}
总结
- 面试很难受,不过我尽力了,算法也复习到了。不过反映出我的问题,就是很多东西看的不够细致,不够深入,先过一遍,后续再继续深化。时间不是很够,加油。
相关文章:

秋招突击——6/16——复习{(单调队列优化DP)——最大子序和,背包模型——宠物小精灵收服问题}——新作{二叉树的后序遍历}
文章目录 引言复习(单调队列优化DP)——最大子序和单调队列的基本实现思路——求可移动窗口中的最值总结 背包模型——宠物小精灵收服问题思路分析参考思路分析 新作二叉树的后续遍历加指针调换 总结 引言 复习 (单调队列优化DP)…...
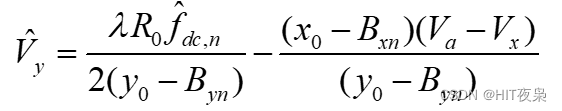
SAR动目标检测系列:【4】动目标二维速度估计
在三大类杂波抑制技术(ATI、DPCA和STAP)中,STAP技术利用杂波与动目标在二维空时谱的差异,以信噪比最优为准则,对地杂波抑制的同时有效保留动目标后向散射能量,有效提高运动目标的检测概率和动目标信号输出信杂比,提供理…...
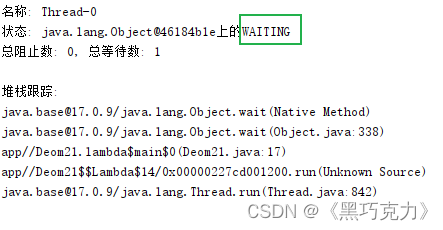
JavaEE多线程(2)
文章目录 1..多线程的安全1.1出现多线程不安全的原因1.2解决多线程不安全的⽅法1.3三种典型死锁场景1.4如何避免死锁问题2.线程等待通知机制2.1等待通知的作用2.2等待通知的方法——wait2.3唤醒wait的方法——notify 1…多线程的安全 1.1出现多线程不安全的原因 线程在系统中…...

中新赛克两款数据安全产品成功获得“可信数安”评估测试证书
6月19日,2024数据智能大会在北京盛大召开。 会上,中国2024年上半年度“可信数安”评估测试证书正式颁发。中新赛克两款参评产品凭借过硬的技术水准和卓越的应用效果,成功获得专项测试证书。 2024年上半年度“可信数安”评估测试通过名单 中新…...

代码随想录——分割回文串(Leetcode 131)
题目链接 回溯 class Solution {List<List<String>> res new ArrayList<List<String>>();List<String> list new ArrayList<String>();public List<List<String>> partition(String s) {backtracking(s, 0);return res;}p…...

Rust 学习方法及学习路线汇总
Rust 学习方法及学习路线汇总 Rust 是一种系统编程语言,旨在提供安全性、并发性和高性能。它是由 Mozilla 公司开发的,于 2010 年首次发布。Rust 能够帮助开发者编写可靠和高效的软件,因此受到了广泛的关注和认可。 如果你有兴趣学习 Rust&…...

一名女DBA的感谢信,到底发生了什么?
昨日我们收到这样一通来电 “早上九点刚上班便收到业务投诉电话,系统卡顿,接口失败率大增,怀疑数据库问题。打开运维平台发现是国产库,生无可恋,第一次生产环境遇到国产库性能问题,没什么排查经验…...
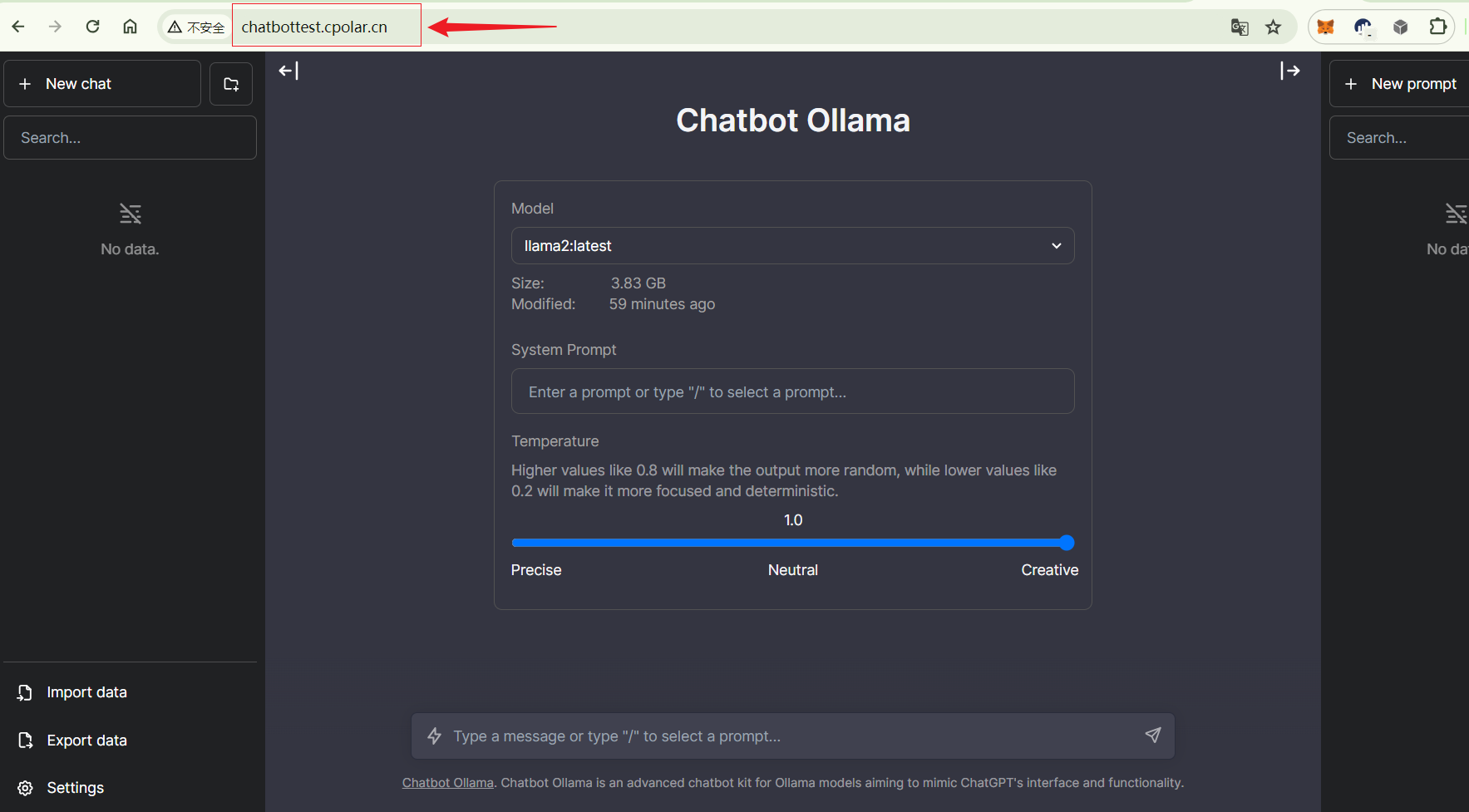
群晖NAS本地部署并运行一个基于大语言模型Llama2的个人本地聊天机器人
前言 本文主要分享如何在群晖 NAS 本地部署并运行一个基于大语言模型 Llama 2 的个人本地聊天机器人并结合内网穿透工具发布到公网远程访问。本地部署对设备配置要求高一些,如果想要拥有比较好的体验,可以使用高配置的服务器设备. 目前大部分大语言模型的产品都是基于网络线上…...
HarmonyOS模拟器(phone-x86-api9)一直卡顿的解决方法
在DevEco Studio 3.1.1 Release版本中的Device Manager中创建本地的模拟器,创建phone-x86-api9模拟器成功,但是启动该新建的模拟器一直显示"HarmonyOS"logo图片,然后一直卡在这里,运行结果如下所示: 检查模…...

排序题目:有序数组的平方
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:有序数组的平方 出处:977. 有序数组的平方 难度 2 级 题目描述 要求 给定按非递减顺序排序的整…...

PPT可以转换成Word吗?归纳了三种转换方式
PPT可以转换成Word吗?在当今快节奏的工作和学习环境中,不同格式文件之间的转换变得日益重要。PPT作为演示文稿制作的首选工具,广泛应用于会议演讲、教育培训等多个场景,而Word则是文档编辑与编排的基石。为了便于进一步编辑、分享…...
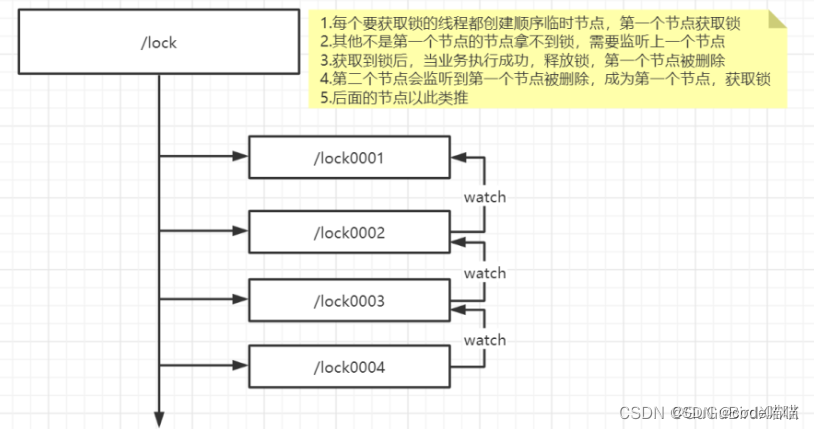
分布式锁三种方案
基于数据库的分布式锁(基于主键id和唯一索引) 1基于主键实现分布式锁 2基于唯一索引实现分布式锁 其实原理一致,都是采用一个唯一的标识进行判断是否加锁。 原理:通过主键或者唯一索性两者都是唯一的特性,如果多个…...

【HarmonyOS NEXT】har 包的构建生成过程
Har模块文件结构 构建HAR 打包规则 开源HAR除了默认不需要打包的文件(build、node_modules、oh_modules、.cxx、.previewer、.hvigor、.gitignore、.ohpmignore)和.gitignore/.ohpmignore中配置的文件,cpp工程的CMakeLists.txt,…...
)
从0开发一个Chrome插件:项目实战——翻译插件(附带申请谷歌翻译、百度翻译教程)
前言 这是《从0开发一个Chrome插件》系列的第十八篇文章,本系列教你如何从0去开发一个Chrome插件,每篇文章都会好好打磨,写清楚我在开发过程遇到的问题,还有开发经验和技巧。 专栏: 从0开发一个Chrome插件:什么是Chrome插件?从0开发一个Chrome插件:开发Chrome插件的必…...

查看nginx安装/配置路径,一个服务器启动两个nginx
查看nginx安装/配置路径 查看nginx的pid: ps -ef | grep nginx查看pid对应服务的启动路径 ll /proc/2320/exe使用检查配置文件命令,查看配置文件位置 /usr/local/nginx/sbin/nginx -t一个服务启动两个nginx 拷贝一份程序,cpbin是我自己创…...

JavaScript中 Map与reduce的应用
1. Map:映射新世界 Map构造函数创建一个新Map对象,它允许你以键值对的形式存储数据,提供了一种更加灵活的数据结构。与传统的对象相比,Map允许任何值(包括对象)作为键,而且具有更好的性能表现。…...

1688商品详情API:一键解锁海量批发数据
引言 1688作为阿里巴巴旗下的B2B交易平台,拥有庞大的商品数据库和丰富的供应商资源。对于想要获取商品详细信息的开发者和企业而言,1688提供的API接口是获取一手数据的关键途径。本文将详细介绍如何使用1688商品详情API,包括注册、获取API密…...
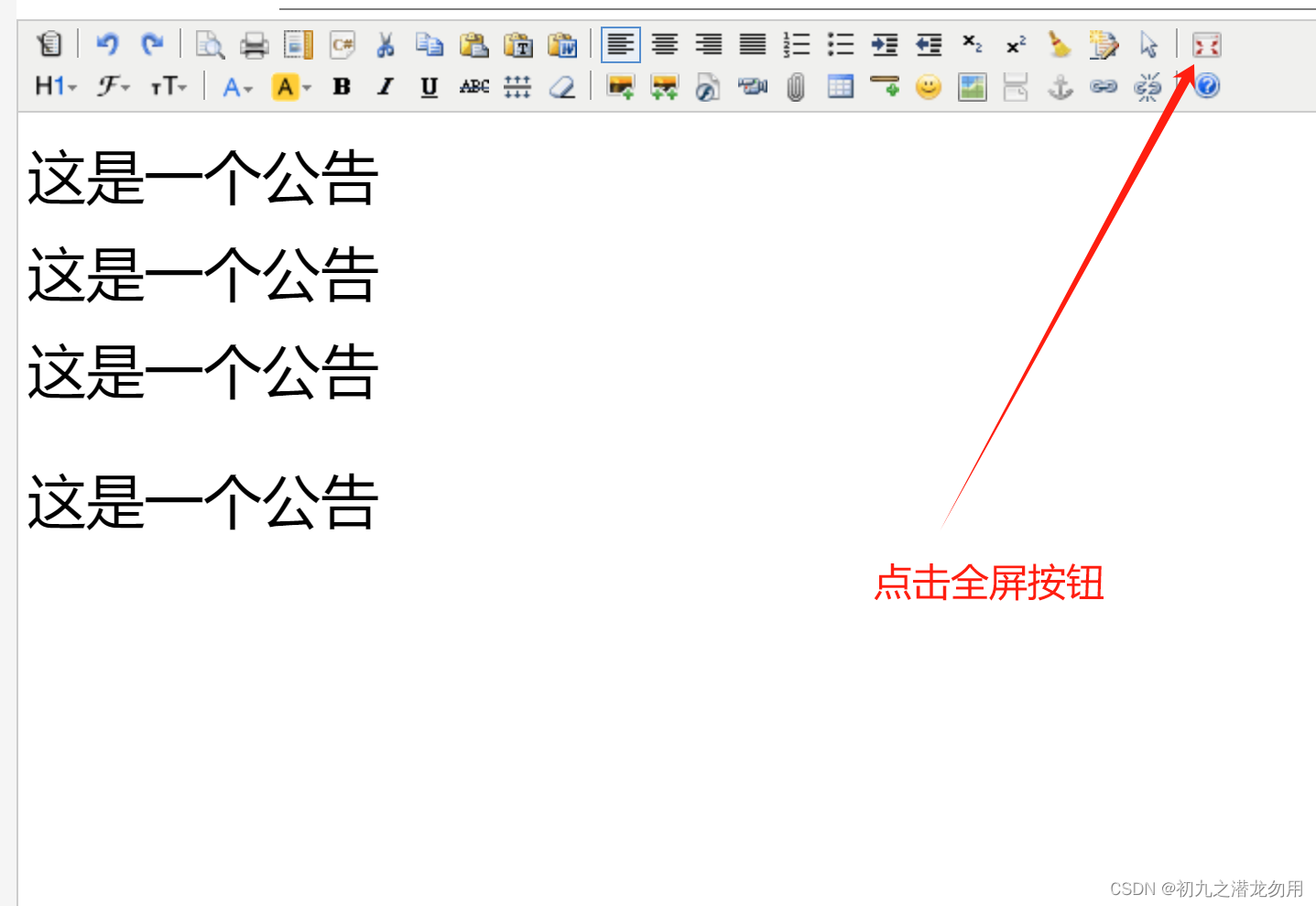
C#结合JS 修改解决 KindEditor 弹出层问题
目录 问题现象 原因分析 范例运行环境 解决问题 修改 kindeditor.js C# 服务端更新 小结 问题现象 KindEditor 是一款出色的富文本HTML在线编辑器,关于编辑器的详细介绍可参考我的文章《C# 将 TextBox 绑定为 KindEditor 富文本》,这里我们讲述在…...
二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面
二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面 二开的精美UI站长源码分享论坛网站源码 可切换皮肤界面...
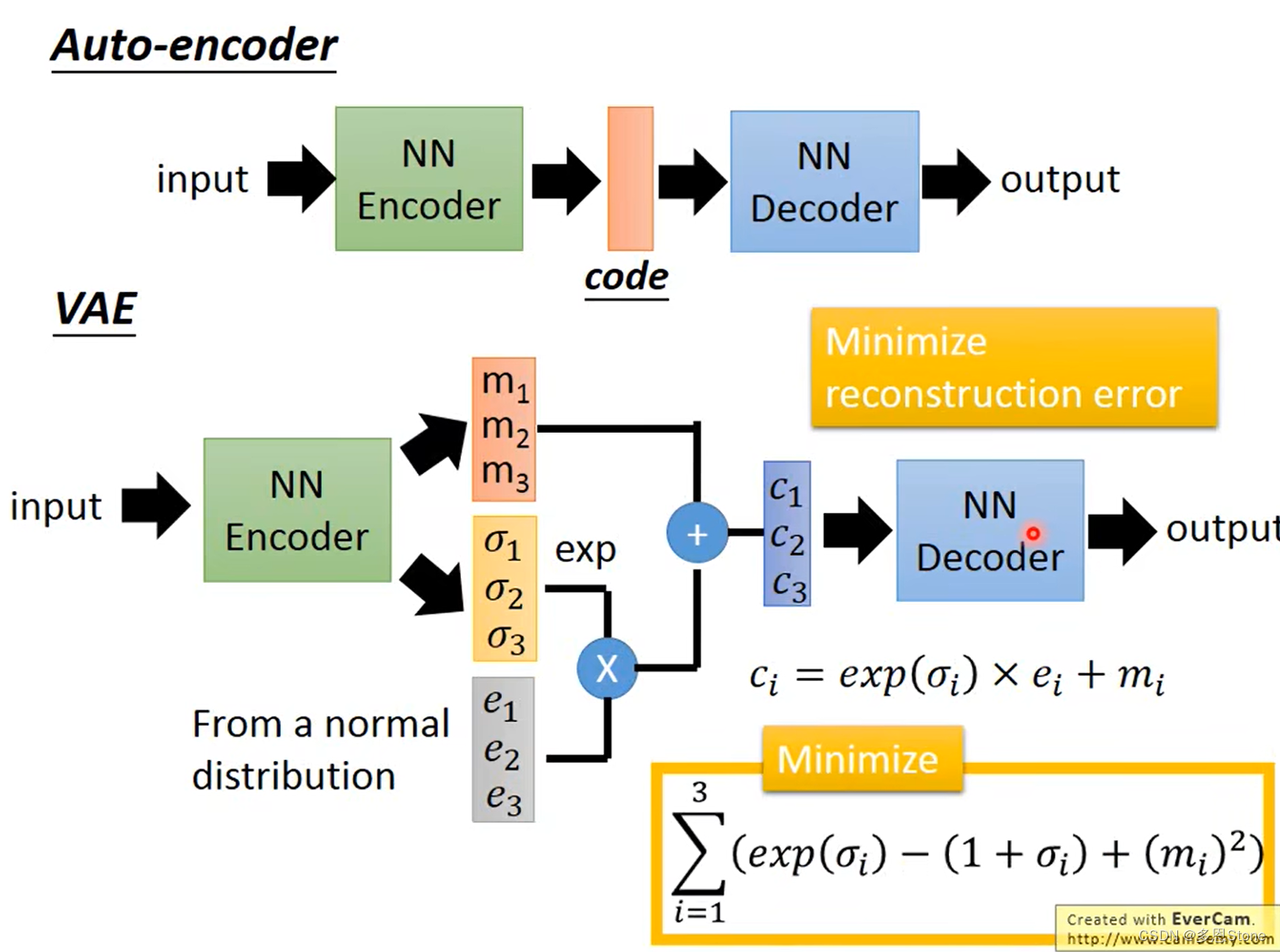
【diffusers极速入门(三)】生成的图像尺寸与 UNet 和 VAE 之间的关系
先上结论,一句话总结即: SD 图片的输入\输出尺寸(高或宽) Unet 输入\输出的样本尺寸(高或宽) x VAE 的缩放尺寸 在使用生成模型时,特别是图像生成任务中,理解 UNet 和 VAE…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
