jQuery如何把单选框设置为选中状态
在网页开发中,我们经常需要使用表单元素来收集用户数据。其中,单选框(radio button)是一种常见的表单元素,用于从一组选项中选择一个。使用jQuery,我们可以轻松地控制这些单选框的状态,包括将它们设置为选中状态。
1. 单选框的HTML结构
首先,让我们看一个简单的单选框的HTML结构:
<form><input type="radio" id="radio1" name="radios" value="option1"><label for="radio1">选项1</label><input type="radio" id="radio2" name="radios" value="option2"><label for="radio2">选项2</label><!-- 可以有更多选项 -->
</form>
在这个例子中,我们有两个单选框,它们的name属性相同(radios),但id和value属性不同。由于它们的name属性相同,所以它们属于同一组单选框。
2. 使用jQuery设置单选框为选中状态
现在,让我们看看如何使用jQuery将某个单选框设置为选中状态。假设我们想要将id为radio2的单选框设置为选中状态,我们可以这样做:
// 确保在DOM加载完成后执行
$(document).ready(function() {// 使用jQuery选择器找到单选框并设置其属性为checked$('#radio2').prop('checked', true);
});
在上面的代码中,我们首先使用$(document).ready()函数来确保在DOM完全加载后再执行我们的代码。然后,我们使用jQuery选择器$('#radio2')来找到id为radio2的单选框,并使用.prop()函数将其checked属性设置为true,从而将其设置为选中状态。
3. 注意事项
- 当设置单选框的选中状态时,使用
.prop()函数而不是.attr()函数是更好的选择。因为.prop()函数用于设置元素的属性,而.attr()函数用于设置元素的HTML属性。对于像checked、selected和disabled这样的布尔属性,使用.prop()函数更为合适。 - 如果你想要取消选中所有单选框,你可以使用
$('input[type="radio"][name="radios"]').prop('checked', false);这样的选择器来选择所有name为radios的单选框,并将它们的checked属性设置为false。 - 确保你的jQuery库已经正确加载到页面中,否则上述代码将无法正常工作。你可以将jQuery库通过CDN或本地文件的方式引入到你的HTML文件中。
相关文章:

jQuery如何把单选框设置为选中状态
在网页开发中,我们经常需要使用表单元素来收集用户数据。其中,单选框(radio button)是一种常见的表单元素,用于从一组选项中选择一个。使用jQuery,我们可以轻松地控制这些单选框的状态,包括将它…...
Mware Fusion Pro 13 mac版:一键掌控虚拟世界
VMware Fusion Pro 13是一款功能卓越的虚拟化软件,专为Mac操作系统量身打造。这款软件为用户提供了一个一站式的虚拟化解决方案,能够满足各种多样化的需求。 VMware Fusion Pro 13 Mac获取 VMware Fusion Pro 13的强大之处在于其采用了最 先进的虚拟化…...
PTA - 函数的定义与调用
编写一个名为collatz()的函数,它有一个名为number的参数: 如果number是偶数,那么collatz()就打印number加上2如果number是奇数,那么collatz()就打印number乘以2 函数接口定义: def collatz(number)裁判测试程序样例: /* 请在这里填写答案…...
Solr7.4.0报错org.apache.solr.common.SolrException
文章目录 org.apache.solr.common.SolrException: Exception writing document id MATERIAL-99598435990497269125316 to the index; possible analysis error: cannot change DocValues type from NUMERIC to SORTED_NUMERIC for field "opt_time"Exception writing…...
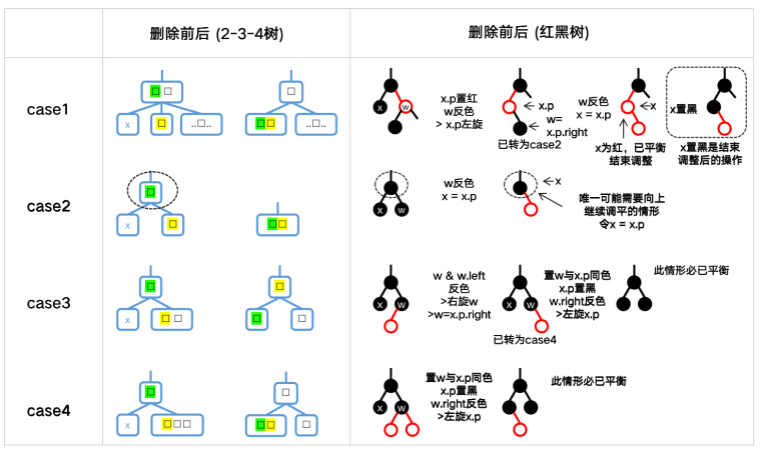
从2-3-4树开始理解红黑二叉树(JAVA代码手撸版)
经典的红黑二叉树在新增/删除数据时维持自平衡始终对应着一个2-3-4 树。本文只关注2-3-4 对应的经典红黑二叉树。 暂时不考虑 2-3 树对应的左倾红黑二叉树。 背景知识 2-3-4 树简介 一棵 2-3-4 树的结点分为 内部结点 (internal nodes) 和 叶子结点 (leaf nodes) ,…...

模板类与继承
1模板类继承普通类(常见) #include<iostream> using namespace std; class AA { public:int m_a;AA(int a) :m_a(a) { cout << "调用了AA的构造函数\n"; }void func1() { cout << "调用func1()…...

随手记:uniapp图片展示,剩余的堆叠
UI效果图: 实现思路: 循环图片数组,只展示几张宽度就为几张图片边距的宽度,剩下的图片直接堆叠展示 点击预览的时候传入当前的下标,如果是点击堆叠的话,下标从堆叠数量开始计算 <template><…...

微服务迁移、重构最佳经验
1. 了解现有的单体应用: - 应用架构和技术栈 要了解现有的应用架构和技术栈,可以采取以下几个步骤: 1. 了解应用的背景和目标:首先要了解应用的背景和目标,包括应用所属的行业、应用的类型(例如Web应用、移动应用等…...

【Python】从0开始的Django基础
Django框架基础 unit01一、Django基础1.1 什么是Django?1.2 安装与卸载1.2.1 Python与Django的版本1.2.2 安装1.2.3 查看Django版本1.2.4 卸载 二、Django项目2.1 概述2.2 创建项目2.3 启动项目2.4 项目的目录结构2.5 配置 三、URL 调度器3.2 定义URL路由3.2 定义首页的路由3.…...
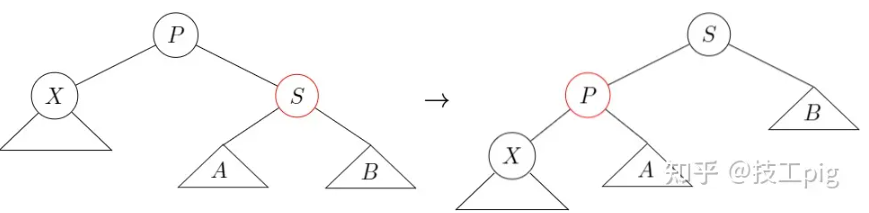
红黑树(数据结构篇)
数据结构之红黑树 红黑树(RB-tree) 概念: 红黑树是AVL树的变种,它是每一个节点或者着成红色,或者着成黑色的一棵二叉查找树。对红黑树的操作在最坏情形下花费O(logN)时间,它的插入操作使用的是非递归形式实现红黑树的高度最多是…...
)
高级视频编码器性能对比(H265、VP9、AV1)
1、背景介绍 目前在视频编解码器中,H264已经成为绝对的主流,被大部分设备、浏览器所支持。虽然有更先进的编码器推出,但是受限于推广速度和设备支持成本,一直未能成为主流。 今年公司目标是持续降本增效,现在将”屠刀…...
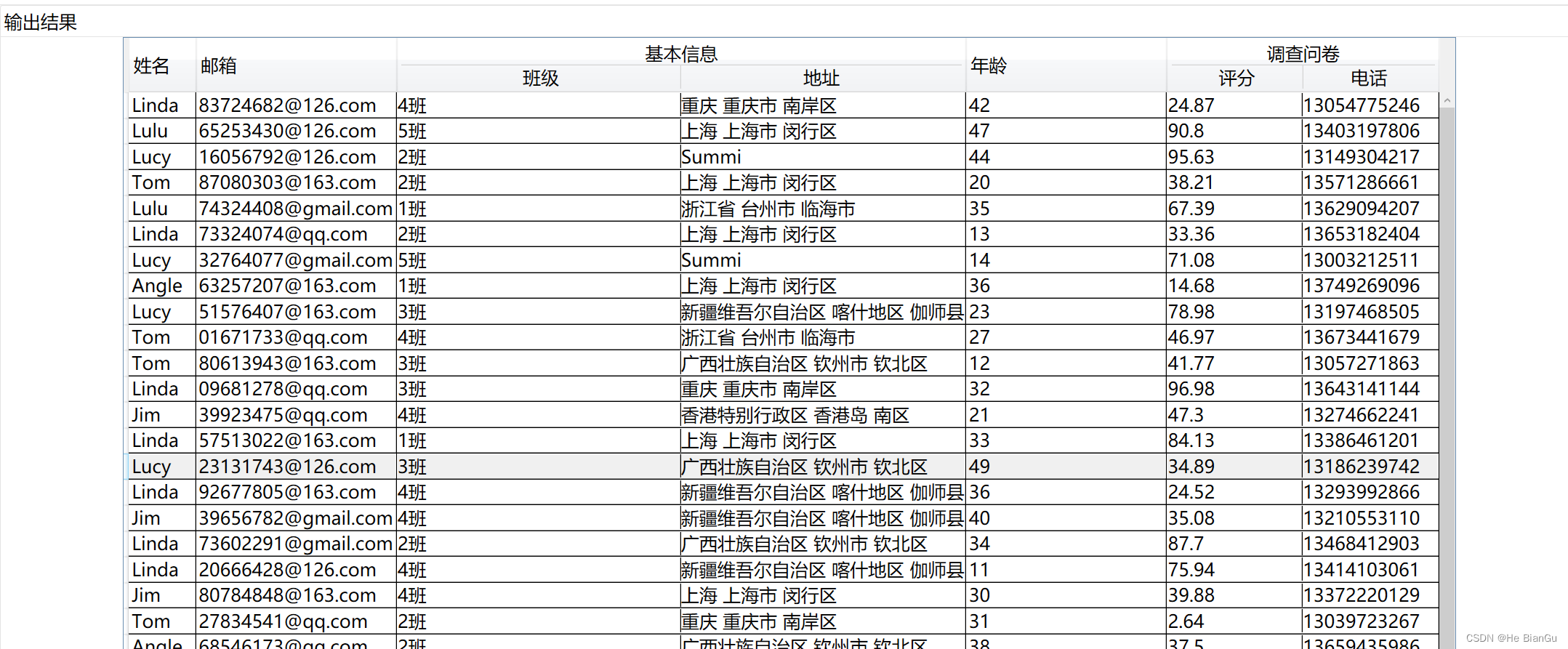
示例:WPF中DataGrid简单设置合并列头
一、目的:应用DataGridTemplateColumn列模板,去拆分列头和单元格布局的方式设置列头合并样式 二、实现 效果如下 三、环境 VS2022 四、示例 应用DataGridTemplateColumn自定义列头信息和单元格信息 <DataGrid AutoGenerateColumns"False"…...
Matlab图像处理——细胞图像的分割和计数显示
一. 项目介绍 使用MATLAB编写的细胞图像分割及计数系统,实现了对图像内细胞的计数,以及对每个细胞周长和面积的测量,并分别展示了分割后的每个细胞的图像。实验步骤共分为图像预处理、图像预分割、空洞填充、黏连细胞分割、细胞个数统计、细胞…...

六爻排盘神机
选修课留了3000字的论文......确实,削微有那么一点小困难…… 但是,倘若我拿出已经占了6419个字符的 “六爻排盘神机” ,阁下…应该…不会…骂我吧 且看,六爻排盘神机! import random import datetime from lunarcale…...

【ARMv8/v9 GIC 系列 2.1 -- GIC SPI 中断的 pending 和 clear pending 配置】
文章目录 GIC Pending 和 Clear PendingGICD_ISPENDR<n>GICD_ICPENDR<n>参数<n>编号解释使用举例设置中断ID 100为挂起状态清除中断ID 100的挂起状态 代码实现小结 GIC Pending 和 Clear Pending 在ARMv8体系结构中,GICD_ISPENDR<n> 和 GI…...
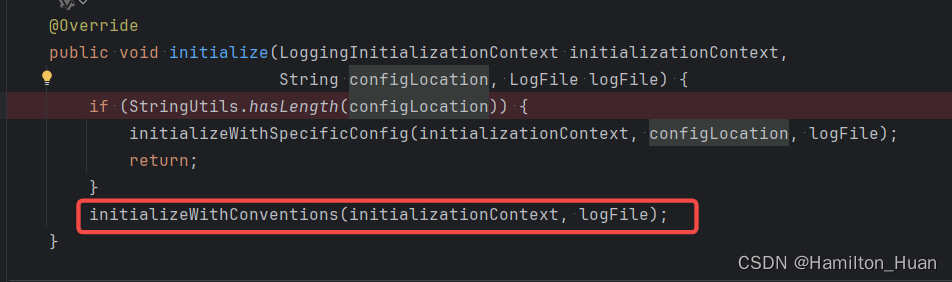
SpringBoot集成logback初始化源码解析(部分)
一.SpringBoot配置扩展点 SpringBoot日志模块使用监听的方式进行初始化,在SpringBoot项目启动后,会通知日志监听器 在日志监听器中ApplicationStartingEvent事件用来确定到底使用哪个日志系统,logback log4j等 在日志监听器中ApplicationEn…...
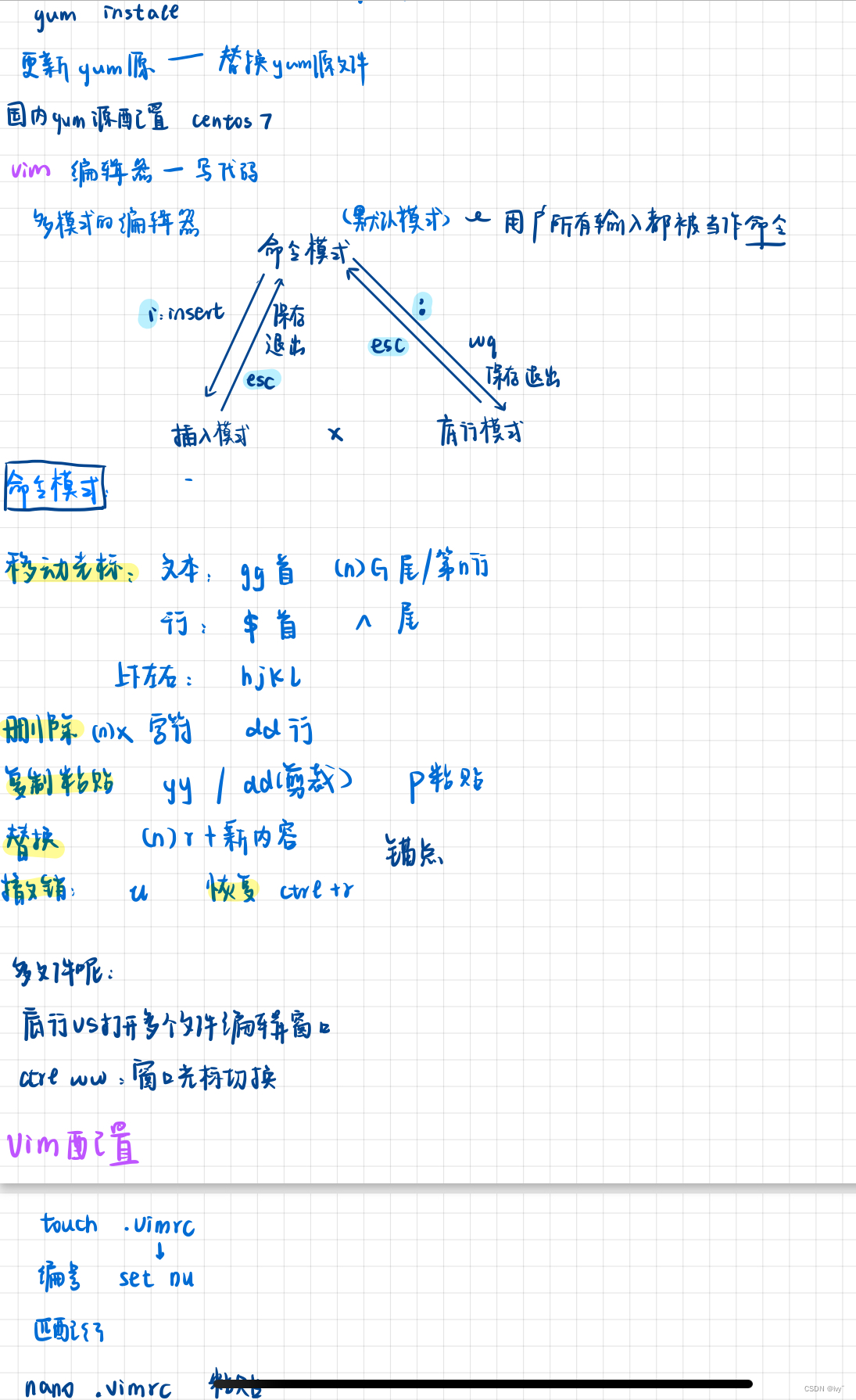
【Linux工具】yum软件包管理器与Vim编辑器的高效运用
目录 Linux 软件包管理器 YUM 什么是软件包 安装工具 rzsz 及注意事项 查看软件包 安装和卸载软件 安装软件 卸载软件 Linux 开发工具 编辑器 - Vim 使用 编辑 Vim 与 Vi 的区别 Vim 的基本概念 三种模式 Vim 的基本操作 操作尝试: Vim 命令集解释…...

Matlab数学建模实战应用:案例4 - 图像处理
目录 前言 一、图像处理基础 二、Matlab图像处理工具箱 三、案例:图像锐化、去噪和分割 步骤 1:读取和显示图像 步骤 2:图像锐化 步骤 3:图像去噪 步骤 4:图像分割 完整代码示例 四、实际应用 实例总结 总…...
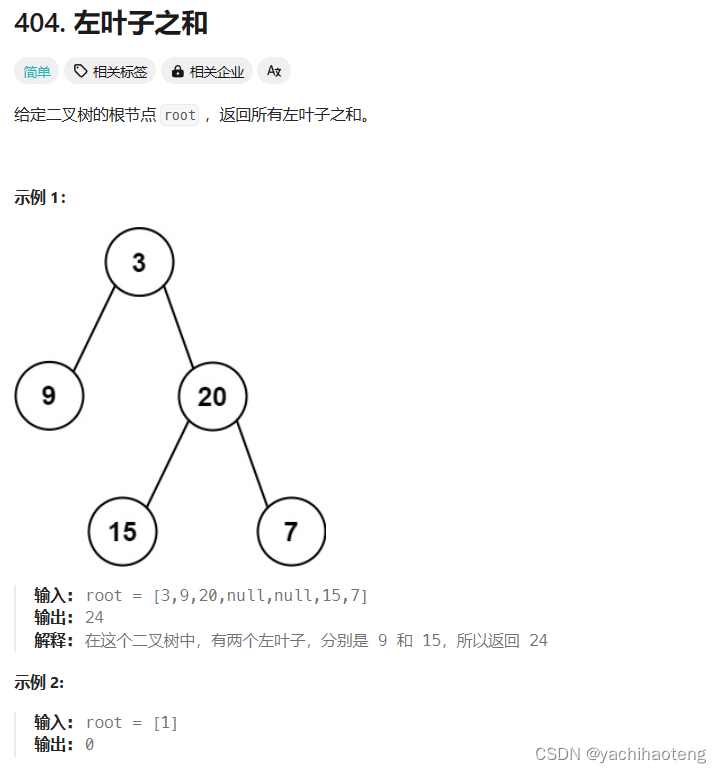
Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C 目录 257.完全二叉树的节点个数 110.平衡二叉树 257.二叉树的所有路径 404.左叶子之和 总结 257.完全二叉树的节点个数 文档讲解:代码随想录完全二叉树的节点个数 视频讲解…...

Python 基础:异常
目录 一、异常概念二、处理异常2.1 抛出异常2.2 使用 try-except 代码块2.3 使用 try-except-else 代码块2.4 静默失败 三、总结 遇到看不明白的地方,欢迎在评论中留言呐,一起讨论,一起进步! 本文参考:《Python编程&a…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
