一步一步用numpy实现神经网络各种层
1. 首先准备一下数据
if __name__ == "__main__":data = np.array([[2, 1, 0],[2, 2, 0],[5, 4, 1],[4, 5, 1],[2, 3, 0],[3, 2, 0],[6, 5, 1],[4, 1, 0],[6, 3, 1],[7, 4, 1]])x = data[:, :-1]y = data[:, -1]for epoch in range(1000):...
2. 实现Softmax+CrossEntropy层
单独求softmax层有点麻烦, 将softmax+entropy一起求导更方便。
假设对于输入向量 ( x 1 , x 2 , x 3 ) (x_1, x_2, x_3) (x1,x2,x3), 则对应的Loss为:
L = − ∑ i = 1 C y i ln p i = − ( y 1 ln p 1 + y 2 ln p 2 + y 3 ln p 3 ) \begin{align*} L&=-\sum_{i=1}^Cy_i \ln p^i \\ &=-(y_1\ln p_1+y_2\ln p_2+y_3\ln p_3) \end{align*} L=−i=1∑Cyilnpi=−(y1lnp1+y2lnp2+y3lnp3)
其中 y i y_i yi为ground truth, 为one-hot vector. p i p_i pi为输出概率。
p 1 = e x 1 e x 1 + e x 2 + e x 3 p 2 = e x 2 e x 1 + e x 2 + e x 3 p 3 = e x 3 e x 1 + e x 2 + e x 3 p_1=\frac{e^{x_1}}{e^{x_1}+e^{x_2}+e^{x_3}}\\ p_2=\frac{e^{x_2}}{e^{x_1}+e^{x_2}+e^{x_3}}\\ p_3=\frac{e^{x_3}}{e^{x_1}+e^{x_2}+e^{x_3}}\\ p1=ex1+ex2+ex3ex1p2=ex1+ex2+ex3ex2p3=ex1+ex2+ex3ex3
则偏导为
∂ L ∂ x 1 = − y 1 1 p 1 ∗ ∂ p 1 ∂ x 1 − y 2 1 p 2 ∗ ∂ p 2 ∂ x 1 − y 3 1 p 3 ∗ ∂ p 3 ∂ x 1 = − y 1 1 p 1 ∗ e x 1 ∗ ( e x 1 + e x 2 + e x 3 ) − e x 1 ∗ e x 1 ( e x 1 + e x 2 + e x 3 ) 2 − y 2 1 p 2 ∗ − e x 2 ∗ e x 1 ( e x 1 + e x 2 + e x 3 ) 2 − y 3 1 p 3 ∗ − e x 3 ∗ e x 1 ( e x 1 + e x 2 + e x 3 ) 2 = − y 1 1 p 1 ( p 1 ∗ p 2 + p 1 ∗ p 3 ) − y 2 1 p 2 ( − p 1 ∗ p 2 ) − y 3 1 p 3 ( − p 1 ∗ p 3 ) = − y 1 ( p 2 + p 3 ) + y 2 ∗ p 2 + y 3 ∗ p 3 = − y 1 ( 1 − p 1 ) + y 2 ∗ p 1 + y 3 ∗ p 1 = y 1 ( p 1 − 1 ) + y 2 ∗ p 1 + y 3 ∗ p 1 \begin{align*} \frac{\partial L}{\partial x_1} &= -y_1\frac{1}{p_1}*\frac{\partial p_1}{\partial x_1} - y_2\frac{1}{p_2}*\frac{\partial p_2}{\partial x_1} - y_3\frac{1}{p_3}*\frac{\partial p_3}{\partial x_1} \\ &= -y_1\frac{1}{p_1} * \frac{e^{x_1} * (e^{x_1}+e^{x_2}+e^{x_3})-e^{x_1}*e^{x_1}}{(e^{x_1}+e^{x_2}+e^{x_3})^2} \\ &\quad\quad-y_2\frac{1}{p_2}*\frac{-e^{x_2}*e^{x_1}}{{(e^{x_1}+e^{x_2}+e^{x_3})^2}}\\ &\quad\quad-y_3\frac{1}{p_3}*\frac{-e^{x_3}*e^{x_1}}{{(e^{x_1}+e^{x_2}+e^{x_3})^2}}\\ &=-y_1\frac{1}{p_1}(p_1*p_2+p_1*p_3)\\ &\quad\quad -y_2\frac{1}{p_2}(-p_1*p_2)\\ &\quad\quad -y_3\frac{1}{p_3}(-p_1*p_3)\\ &=-y1(p_2+p_3)+y_2*p_2+y_3*p_3\\ &=-y_1(1-p_1)+y_2*p_1+y_3*p_1\\ &=y_1(p_1-1)+y_2*p_1+y_3*p_1 \end{align*} ∂x1∂L=−y1p11∗∂x1∂p1−y2p21∗∂x1∂p2−y3p31∗∂x1∂p3=−y1p11∗(ex1+ex2+ex3)2ex1∗(ex1+ex2+ex3)−ex1∗ex1−y2p21∗(ex1+ex2+ex3)2−ex2∗ex1−y3p31∗(ex1+ex2+ex3)2−ex3∗ex1=−y1p11(p1∗p2+p1∗p3)−y2p21(−p1∗p2)−y3p31(−p1∗p3)=−y1(p2+p3)+y2∗p2+y3∗p3=−y1(1−p1)+y2∗p1+y3∗p1=y1(p1−1)+y2∗p1+y3∗p1
同理:
∂ L ∂ x 2 = y 1 ∗ p 2 + y 2 ( p 2 − 1 ) + y 3 ∗ p 2 ∂ L ∂ x 3 = y 1 ∗ p 3 + y 2 p 3 + y 3 ∗ ( p 3 − 1 ) \frac{\partial L}{\partial x_2}=y_1*p_2+y_2(p_2-1)+y_3*p_2\\ \frac{\partial L}{\partial x_3}=y_1*p_3+y_2p_3+y_3*(p_3-1) ∂x2∂L=y1∗p2+y2(p2−1)+y3∗p2∂x3∂L=y1∗p3+y2p3+y3∗(p3−1)
当 y 1 = 1 y_1=1 y1=1时, 对应的导数为 ( p 1 − 1 , p 2 , p 3 ) (p1-1, p_2, p_3) (p1−1,p2,p3). 当 y 2 = 1 y_2=1 y2=1时,对应的导数为: ( p 1 , p 2 − 1 , p 3 ) (p_1, p2-1, p3) (p1,p2−1,p3).
例如求得概率为 ( 0.2 , 0.3 , 0.5 ) (0.2, 0.3, 0.5) (0.2,0.3,0.5), label为 ( 0 , 0 , 1 ) (0, 0, 1) (0,0,1), 则导数为 ( 0.2 , 0.3 , − 0.5 ) (0.2, 0.3, -0.5) (0.2,0.3,−0.5)
python代码为:
注意求softmax时需要np.exp(x-np.max(x, axis=1, keepdims=True))防止指数运算溢出。
class Softmax:def __init__(self, n_classes):self.n_classes = n_classesdef forward(self, x, y):prob = np.exp(x-np.max(x, axis=1, keepdims=True))prob /= np.sum(prob, axis=1, keepdims=True)# 选出y==1位置的概率loss = -np.sum(np.log(prob[np.arange(len(y), y])) / len(y)self.grad = prob.copy()self.grad[np.arange(len(y), y] -= 1"""因为后面求导数都是直接np.sum而不是np.mean, 因此这里mean一次就可以了"""self.grad /= len(y) return prob, lossdef backward(self):return self.grad
3. 单独的CrossEntropy
python代码为:
class Entropy:def __init__(self, n_classes):self.n_classes = n_classesself.grad = Nonedef forward(self, x, y):# x: (b, c), y: (b)b = y.shape[0]one_hot_y = np.zeros((b, self.n_classes))one_hot_y[range(len(y)), y] = 1self.grad = one_hot_y * -1 / xreturn np.mean(-one_hot_y * np.log(x), axis=0)def backward(self):return self.grad
2. 单独的Softmax层
from einops import repeat, rearrange, einsum
class Softmax:def __init__(self):def forward(self, x):# x: (b, c)x_exp = np.exp(x)self.output = x_xep / np.sum(x_exp, axis=1, keep_dims=True)return self.outputdef backward(self, prev_grad):b, c = self.output.shapeo = repeat(self.output, 'b c -> b c r', r=c)I = repeat(np.eye(x.shape[1]), 'c1 c2 -> b c1 c2', b=b)self.grad = o * (I - rearrange(o, 'b c1 c2 -> b c2 c1'))return einsum(self.grad, grad[..., None], 'b c c, b c m -> b c m')[..., 0]
3. Linear层
注意更新 w w w时用的 d w d_w dw, 但是往上一层传递的是 d x d_x dx。因为上一层需要 d L / d o u t dL/d_{out} dL/dout, 而本层的输入 x x x即是上一次层的输出 d L / d o u t = d L / d x dL/d_{out} = dL/dx dL/dout=dL/dx
class Linear:def __init__(self, in_channels, out_channels, lr):self.lr = lrself.w = np.random.rand(in_channels, out_channels)self.b = np.random.rand(out_channels)def forward(self, x):self.x = xreturn x@self.w + self.bdef backward(self, grad):dx = einsum(prev_grad, rearrange(self.w, 'w1 w2 -> w2 w1'), 'c1 b, b c2 -> c1 c2')dw = einsum(rearrange(self.x, 'b c -> c b'), prev_grad, 'c1 b, b c2 -> c1 c2')db = np.sum(prev_grad, axis=0)self.w -= self.lr * dwself.b -= self.lr * db"""注意这里往上一层传递的是dx, 因为上一层需要dL/d_out, 而本层的输入x即是上一次层的输出dL/d_out = dL/dx"""return dx5. 完整训练代码
from einops import *
import numpy as npclass Softmax:def __init__(self, train=True):self.grad = Noneself.train = traindef forward(self, x, y):prob = np.exp(x-np.max(x, axis=1, keepdims=True))prob /= np.sum(prob, axis=1, keepdims=True)if self.train:loss = -np.sum(np.log(prob[range(len(y)), y]))/len(y)self.grad = prob.copy()self.grad[range(len(y)), y] -= 1self.grad /= len(y)return prob, losselse:return probdef backward(self):return self.gradclass Linear:def __init__(self, in_channels, out_channels, lr):self.w = np.random.rand(in_channels, out_channels)self.b = np.random.rand(out_channels)self.lr = lrdef forward(self, x):self.x = xoutput = einsum(x, self.w, 'b c1, c1 c2 -> b c2') + self.breturn outputdef backward(self, prev_grad):cur_grad = einsum(rearrange(self.x, 'b c -> c b'), prev_grad, 'c1 b, b c2 -> c1 c2')self.w -= self.lr * cur_gradself.b -= self.lr * np.sum(prev_grad, axis=0)return cur_gradclass Network:def __init__(self, in_channels, out_channels, n_classes, lr):self.lr = lrself.linear = Linear(in_channels, out_channels, lr)self.softmax = Softmax()def forward(self, x, y=None):out = self.linear.forward(x)out = self.softmax.forward(out, y)return outdef backward(self):grad = self.softmax.backward()grad = self.linear.backward(grad)return gradif __name__ == "__main__":data = np.array([[2, 1, 0],[2, 2, 0],[5, 4, 1],[4, 5, 1],[2, 3, 0],[3, 2, 0],[6, 5, 1],[4, 1, 0],[6, 3, 1],[7, 4, 1]])# x = np.concatenate([np.array([[1]] * data.shape[0]), data[:, :2]], axis=1)x = data[:, :-1]y = data[:, -1:].flatten()net = Network(2, 2, 2, 0.1)# loss_fn = CrossEntropy(n_classes=2)for epoch in range(500):prob, loss = net.forward(x, y)# loss = loss_fn.forward(out, y)# grad_ = loss_fn.backward()grad = net.backward()print(loss)net.softmax.train = Falseprint(net.forward(np.array([[0, 0], [0, 4], [8, 6], [10, 10]])), y)
相关文章:

一步一步用numpy实现神经网络各种层
1. 首先准备一下数据 if __name__ "__main__":data np.array([[2, 1, 0],[2, 2, 0],[5, 4, 1],[4, 5, 1],[2, 3, 0],[3, 2, 0],[6, 5, 1],[4, 1, 0],[6, 3, 1],[7, 4, 1]])x data[:, :-1]y data[:, -1]for epoch in range(1000):...2. 实现SoftmaxCrossEntropy层…...
)
vue学习(二)
9.vue中的数据代理 通过vm对象来代理data对象中的属性操作(读写),目的是为了更加方便操作data中的数据 基本原理:通过Object.defineProperty()把data对象所有属性添加到vm上,为每一个添加到vm上的属性,都增…...
Maven 介绍
Maven open in new window 官方文档是这样介绍的 Maven 的: Apache Maven is a software project management and comprehension tool. Based on the concept of a project object model (POM), Maven can manage a projects build, reporting and documentation fr…...

QT截图程序三-截取自定义多边形
上一篇文章QT截图程序,可多屏幕截图二,增加调整截图区域功能-CSDN博客描述了如何截取,具备调整边缘功能后已经方便使用了,但是与系统自带的程序相比,似乎没有什么特别,只能截取矩形区域。 如果可以按照自己…...

Unity的三种Update方法
1、FixedUpdate 物理作用——处理物理引擎相关的计算和刚体的移动 (1) 调用时机:在固定的时间间隔内,而不是每一帧被调用 (2) 作用:用于处理物理引擎的计算,例如刚体的移动和碰撞检测 (3) 特点:能更准确地处理物理…...
[Python学习篇] Python字典
字典是一种可变的、无序的键值对(key-value)集合。字典在许多编程(Java中的HashMap)任务中非常有用,因为它们允许快速查找、添加和删除元素。字典使用花括号 {} 表示。字典是可变类型。 语法: 变量 {key1…...

react项目中如何书写css
一:问题: 在 vue 项目中,我们书写css的方式很简单,就是在 .vue文件中写style标签,然后加上scope属性,就可以隔离当前组件的样式,但是在react中,是没有这个东西的,如果直…...

PostgreSQL源码分析——绑定变量
这里分析一下函数中应用绑定变量的问题,但实际应用场景中,不推荐这么使用。 prepare divplan2(int,int) as select div($1,$2); execute divplan2(4,2);语法解析 分别分析prepare语句以及execute语句。 gram.y中定义 /******************************…...

Zynq学习笔记--了解中断配置方式
目录 1. 简介 2. 工程与代码解析 2.1 Vivado 工程 2.2 Vitis 裸机代码 2.3 关键代码解析 3. 总结 1. 简介 Zynq 中的中断可以分为以下几种类型: 软件中断(Software Generated Interrupt, SGI):由软件触发,通常…...
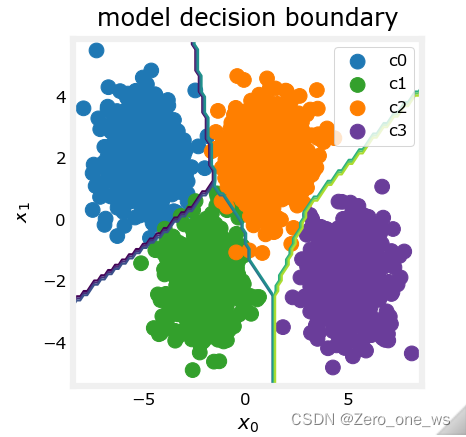
吴恩达机器学习 第二课 week2 多分类问题
目录 01 学习目标 02 实现工具 03 概念与原理 04 应用示例 05 总结 01 学习目标 (1)理解二分类与多分类的原理区别 (2)掌握简单多分类问题的神经网络实现方法 (3)理解多分类问题算法中的激活函数与损失…...

112、路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点 是指没有子节点…...

Vue 封装组件之Input框
封装Input组件:MyInput.vue <template><div class"base-input-wraper"><el-inputv-bind"$attrs"v-on"$listeners"class"e-input":style"inputStyle":value"value":size"size"input&quo…...

一段代码让你了解Java中的抽象
我们先来看一道题! 计算几何对象的面积之和)编写一个方法,该方法用于计算数组中所有几何对象的面积之和。该方法的签名是: public static double sumArea(GeometricObject[] a) 编写一个测试程序,该程序创建一个包含四…...
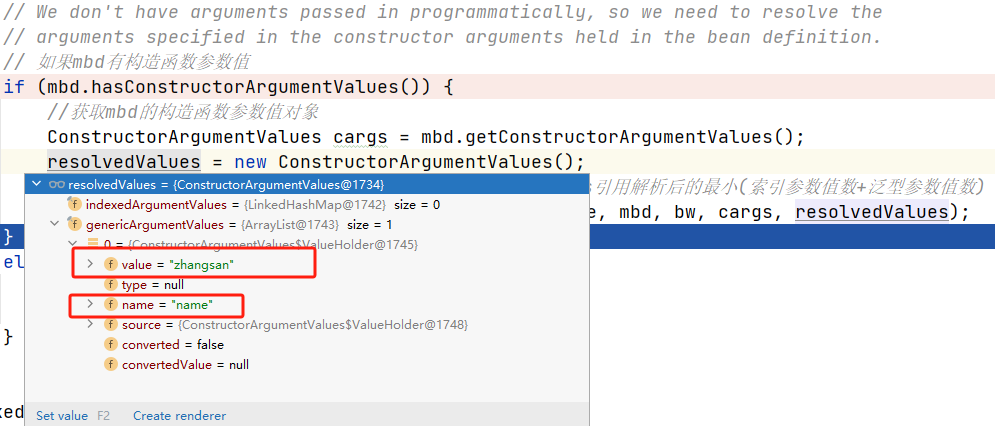
Sping源码(九)—— Bean的初始化(非懒加载)— Bean的创建方式(factoryMethod)
序言 前面文章介绍了在Spring中多种创建Bean实例的方式,包括采用FactoryBean的方式创建对象、使用反射创建对象、自定义BeanFactoryPostProcessor。 这篇文章继续介绍Spring中创建Bean的形式之一——factoryMethod。方法用的不多,感兴趣可以当扩展了解。…...

绝对全网首发,利用Disruptor EventHandler实现在多线程下顺序执行任务
disruptor有两种任务处理器,一个是EventHandler ,另一个是WorkHandler. EventHandler可以彼此独立消费同一个队列中的任务,WorkHandler可以共同竞争消费同一个队列中的任务。也就是说,假设任务队列中有a、b、c、d三个事件,eventHa…...

单例设计模式双重检查的作用
先看双重校验锁的写法 public class Singleton {/*volatile 修饰,singleton new Singleton() 可以拆解为3步:1、分配对象内存(给singleton分配内存)2、调用构造器方法,执行初始化(调用 Singleton 的构造函数来初始化成员变量&am…...
NGINX_十二 nginx 地址重写 rewrite
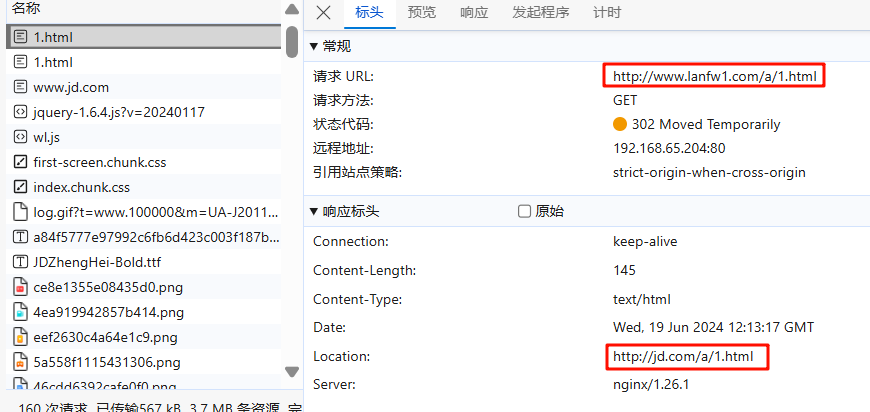
十二 nginx 地址重写 rewrite 1 什么是Rewrite Rewrite对称URL Rewrite,即URL重写,就是把传入Web的请求重定向到其他URL的过程。URL Rewrite最常见的应用是URL伪静态化,是将动态页面显示为静态页面方式的一种技术。比如 http://www.123.com…...
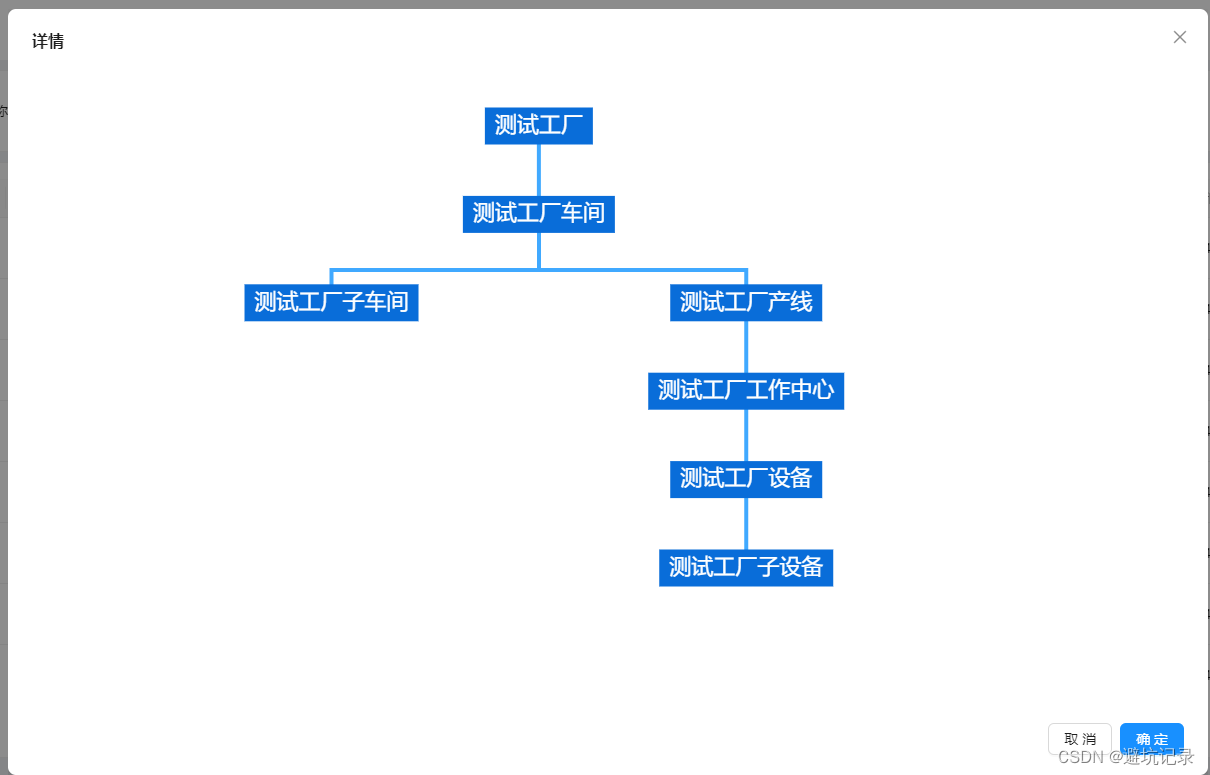
react用ECharts实现组织架构图
找到ECharts中路径图。 然后开始爆改。 <div id{org- name} style{{ width: 100%, height: 650, display: flex, justifyContent: center }}></div> // data的数据格式 interface ChartData {name: string;value: number;children: ChartData[]; } const treeDep…...

坚持刷题|合并有序链表
文章目录 题目思考代码实现迭代递归 扩展实现k个有序链表合并方法一方法二 PriorityQueue基本操作Java示例注意事项 Hello,大家好,我是阿月。坚持刷题,老年痴呆追不上我,消失了一段时间,我又回来刷题啦,今天…...
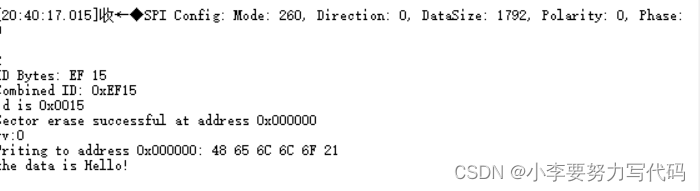
SPI协议——对外部SPI Flash操作
目录 1. W25Q32JVSSIQ背景知识 1.1 64个可擦除块 1.2 1024个扇区(每个块有16个扇区) 1.3 页 1. W25Q32JVSSIQ背景知识 W25Q32JV阵列被组织成16,384个可编程页,每页有256字节。一次最多可以编程256个字节。页面可分为16组(4KB扇区清除&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
