数据结构_二叉树
目录
一、树型结构
二、二叉树
2.1 概念
2.2 特殊的二叉树
2.3 二叉树的性质
2.4 二叉树的存储
2.5 遍历二叉树
2.6 操作二叉树
总结
一、树型结构
树是一种非线性的数据结构,它是由 n(n>=0) 个有限结点组成一个具有层次关系的集合,一棵 n 个结点的树有 n-1 条边。

- 结点的度:一个节点具有的子树个数称为该结点的度。如上图,结点 A 的度为 6。
- 树的度:一棵树中,所有结点度的最大值称为树的度。如上图,树的度为 6。
- 叶子结点 (终端结点):度为 0 的结点称为叶子结点。如上图,B、C、H、I、N 等结点为叶子结点。
- 父结点 (双亲结点):若一个结点含有子结点,则称该结点为其子结点的父节点。如上图,A 是 B 的父结点。
- 根结点:是每棵树的起始结点,即没有父结点的结点。如上图,A 为根结点。
- 子结点 (孩子结点):一个结点含有的子树的根结点,称为该结点的子节点。如上图,B 是 A 的子结点。
- 结点的层次:从根结点开始,根结点为第 1 层,根结点的子结点为第 2 层,以此类推。如上图,结点 A 为第 1 层,结点 B、C、D 等为第 2 层。
- 树的高度 (深度):树中结点的最大层次。如上图,树的高度为 4。
- 分支结点:度不为 0 的结点。
- 兄弟结点:具有相同父结点的结点互为兄弟。
- 堂兄弟结点:父结点在同一层的结点互为堂兄弟。
- 结点的祖先:从根结点到该结点分支上的所有结点。如上图,A 是所有结点的祖先。
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图,所有结点都是 A 的子孙。
- 森林:由 m(m>=0) 棵互不相交的树组成的集合称为森林。
二、二叉树
2.1 概念
一棵二叉树是结点的一个有限集合,二叉树有两种情况:
① 空树;
② 由一个根结点加上两棵分别称为左子树和右子树的二叉树组成。
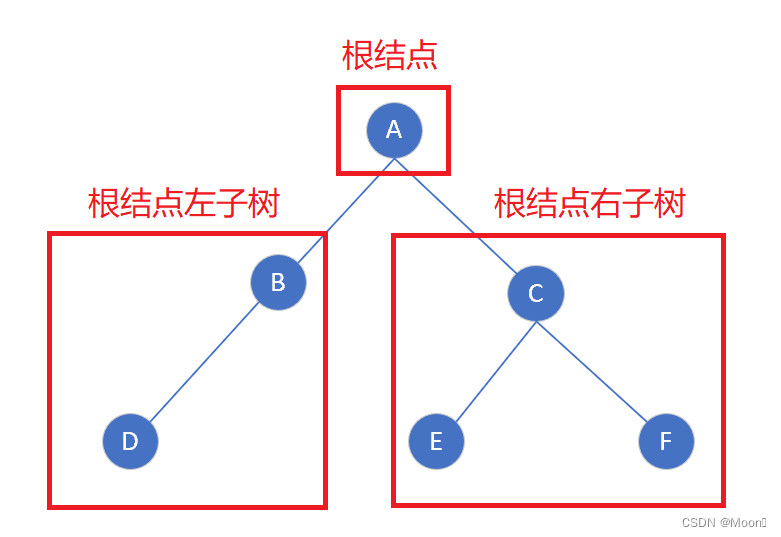
【特点】
1、二叉树不存在度大于 2 的结点;
2、二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
2.2 特殊的二叉树
1、满二叉树:若一棵二叉树每层的结点数都达到最大值,则这棵树就是满二叉树。即若一棵二叉树的高度为 k,且结点总数是 ,则它就是满二叉树。
2、完全二叉树:满二叉树是一种特殊的完全二叉树。对于高度为 K,有 n 个结点的二叉树,当且仅当其每个结点都与高度为 k 的满二叉树中编号从 0 至 n-1 的结点一一对应时称为完全二叉树。

2.3 二叉树的性质
- 一棵非空二叉树的第 k 层上最多有
个结点;
- 高度为 k 的二叉树最大结点数为
;
- 叶子结点个数为
,度为 2 的结点个数为
,则有
;
- 有 n 个结点的完全二叉树高度为
;("[]"为取整)
- 一棵有 n 个结点的完全二叉树,对于其编号为 i 的结点有:
- 若 i > 0,父结点编号:[(i-1) / 2];若 i = 0,则 i 为根结点编号,无父结点。
- 若 2i+1 < n,左孩子编号:2i+1;反之无左孩子。
- 若 2i+2 < n,右孩子编号:2i+2;反之无右孩子。
2.4 二叉树的存储
二叉树的存储结构分为:顺序存储和链式存储。
二叉树的链式存储是通过一个一个结点引用构造出的,例如,孩子表示法和孩子双亲表示法:
//孩子表示法class Node {int val; //数据域Node left; //左孩子Node right; //右孩子}//孩子双亲表示法class Node {int val; //数据域Node left; //左孩子Node right; //右孩子Node parent; //当前节点的父亲节点}2.5 遍历二叉树
【前中后序遍历】
前序(NLR):根结点 → 左子树 → 右子树;(根左右)
中序(LNR):左子树 → 根结点 → 右子树;(左根右)
后序(LRN):左子树 → 右子树 → 根结点;(左右根)

前序:ABDEGCF
中序:DBGEAFC
后序:DGEBFCA
public class BinaryTree {//孩子表示法static class TreeNode {public String val; //数据域public TreeNode left; //左孩子public TreeNode right; //右孩子public TreeNode(String val) {this.val = val;}}//构建树,返回根结点public TreeNode createTree() {TreeNode A = new TreeNode("A");TreeNode B = new TreeNode("B");TreeNode C = new TreeNode("C");TreeNode D = new TreeNode("D");TreeNode E = new TreeNode("E");TreeNode F = new TreeNode("F");TreeNode G = new TreeNode("G");A.left = B;A.right = C;B.left = D;B.right = E;E.left = G;C.left = F;return A;}//前序遍历public void preOrder(TreeNode root) {//若为空树,返回if (root == null) {return;}System.out.print(root.val + " "); //根preOrder(root.left); //左preOrder(root.right); //右}//中序遍历public void inOrder(TreeNode root) {//若为空树,返回if (root == null) {return;}inOrder(root.left);//左System.out.print(root.val + " ");//根inOrder(root.right);//右}//后序遍历public void postOrder(TreeNode root) {//若为空树,返回if (root == null) {return;}postOrder(root.left);//左postOrder(root.right);//右System.out.print(root.val + " ");//根}
}public class Main {public static void main(String[] args) {//创建二叉树对象BinaryTree binaryTree = new BinaryTree();//构建二叉树BinaryTree.TreeNode root = binaryTree.createTree();binaryTree.preOrder(root);//前序:A B D E G C F System.out.println();binaryTree.inOrder(root);//中序:D B G E A F CSystem.out.println();binaryTree.postOrder(root);//后序:D G E B F C A }
}
【层序遍历】
层序遍历:即自上而下、从左至右逐层访问树的结点的遍历过程。
2.6 操作二叉树
采用子问题思路来实现二叉树的操作。
1、获取树中结点个数
//获取树中结点的个数public int size(TreeNode root) {//若为空树,返回if (root == null) {return 0;}//返回根结点的左子树 + 根结点的右子树 + 根结点本身return size(root.left) + size(root.right) + 1;}2、获取树中叶子结点个数
//获取叶子结点的个数public int getLeafNodeCount(TreeNode root) {//若为空树,返回if (root == null) {return 0;}//若无左子树与右子树,便是叶子结点if (root.left == null && root.right == null) {//是叶子结点,返回 1return 1;}//返回根结点的左子树、右子树中的叶子结点return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}3、获取第 K 层结点个数
//获取第 K 层结点的个数public int getKLevelNodeCount(TreeNode root, int k) {//若为空树,返回if (root == null) {return 0;}//第 K 层是第 1 层根结点的第 K-1 层,//也是第 2 层结点的第 K-2 层。//即第 K 层结点的第 1 层,if (k == 1) {return 1;}//返回根结点的左子树、右子树的第 K 层结点return getKLevelNodeCount(root.left, k-1) + getKLevelNodeCount(root.right, k-1);}4、获取二叉树的高度
//获取二叉树的高度public int getHeight(TreeNode root) {//若为空树,返回if (root == null) {return 0;}//左子树高度int leftHeight = getHeight(root.left);//右子树高度int rightHeight = getHeight(root.right);//根结点的左子树与右子树对比,//谁高返回谁 + 根结点本身,即左(右)子树高度 + 1。return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;}5、检测值为 val 的元素是否存在
//检测值为 val 的元素是否存在public TreeNode find(TreeNode root, String val) {//若为空树,返回if (root == null) {return null;}//判断根结点元素if (root.val == val) {return root;}//判断根结点的左子树TreeNode left = find(root.left, val);if (left != null) {return left;}//判断根结点的右子树TreeNode right = find(root.right, val);if (right != null) {return right;}return null;}总结
1、一棵 n 个结点的树有 n-1 条边。
2、二叉树不存在度大于 2 的结点。
3、二叉树的存储结构分为:顺序存储和链式存储。
4、前序(根左右);中序(左根右);后序(左右根)。
5、层序遍历:自上而下、从左至右逐层访问树的结点的遍历过程。
相关文章:

数据结构_二叉树
目录 一、树型结构 二、二叉树 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.5 遍历二叉树 2.6 操作二叉树 总结 一、树型结构 树是一种非线性的数据结构,它是由 n(n>0) 个有限结点组成一个具有层次关系的集合,一棵 n 个…...

Java线程池七个参数详解
ThreadPoolExecutor 是JDK中的线程池实现,这个类实现了一个线程池需要的各个方法,它提供了任务提交、线程管理、监控等方法 下面是 ThreadPoolExecutor 类的构造方法源码,其他创建线程池的方法最终都会导向这个构造方法,共有7个参…...
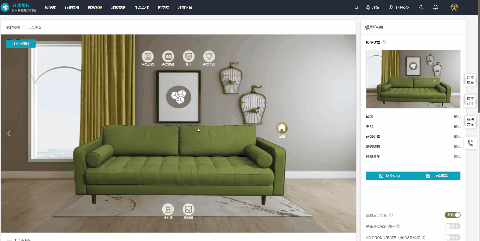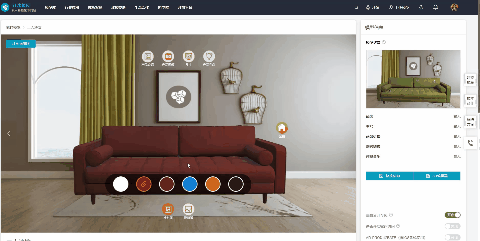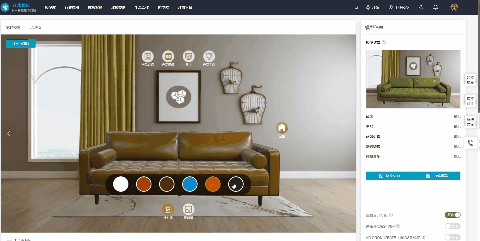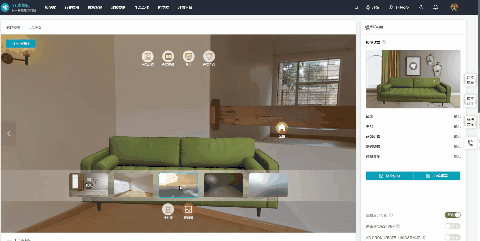
产品Web3D交互展示有什么优势?如何快速制作?
智能互联网时代,传统的图片、文字、视频等产品展示方式,因为缺少互动性,很难引起用户的兴趣,已经逐渐失去了宣传优势。 Web3D交互展示技术的出现,让众多品牌和企业找到了新的方向,线上产品展示不在枯燥无趣…...

Python | Leetcode Python题解之第171题Excel列表序号
题目: 题解: class Solution:def titleToNumber(self, columnTitle: str) -> int:number, multiple 0, 1for i in range(len(columnTitle) - 1, -1, -1):k ord(columnTitle[i]) - ord("A") 1number k * multiplemultiple * 26return n…...
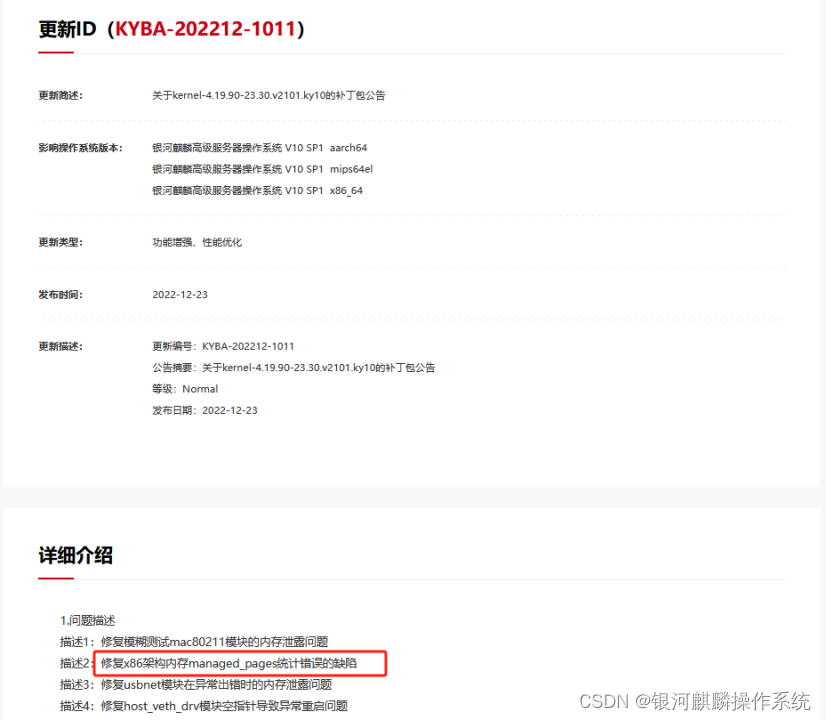
【银河麒麟】高可用触发服务器异常重启,处理机制详解
1.服务器环境以及配置 【机型】物理机 处理器: Intel 内存: 126G 【内核版本】 4.19.90-25.16.v2101.ky10.x86_64 【银河麒麟操作系统镜像版本】 Kylin-Server-10-SP2-Release-Shenzhen-Metro-x86-Build01-20220619 Kylin-HA-10-SP2-Release-S…...
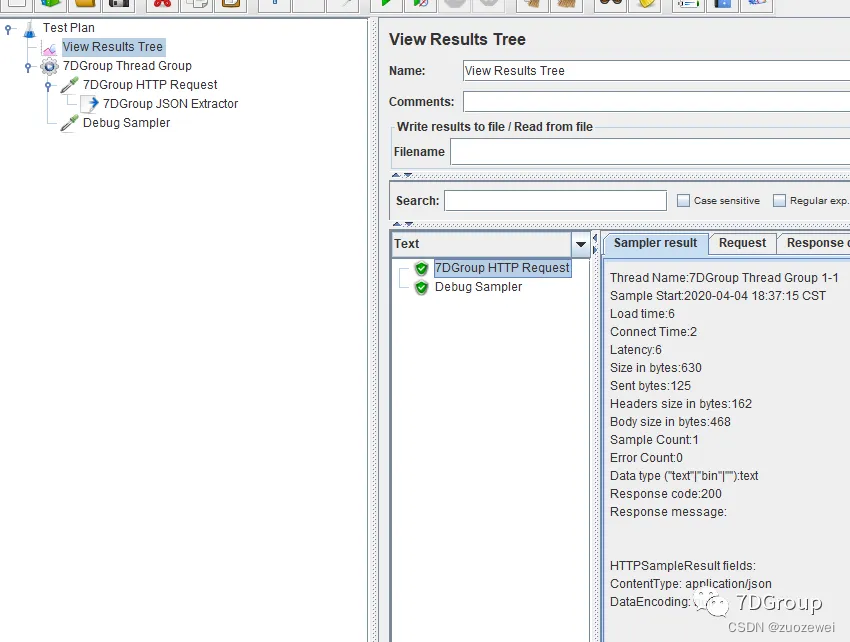
性能工具之 JMeter 常用组件介绍(七)
文章目录 一、后置处理器1、Regular Expression Extractor(正则表达式提取器)2、JSON Extractor(JSON表达式提取器)3、Regular Expression Extractor(正则表达式提取器) 二、小结 本文主要介绍JMeter主流后置处理器的功能 一、后置处理器 从上面可以看出后置处理可以插件挺多&a…...
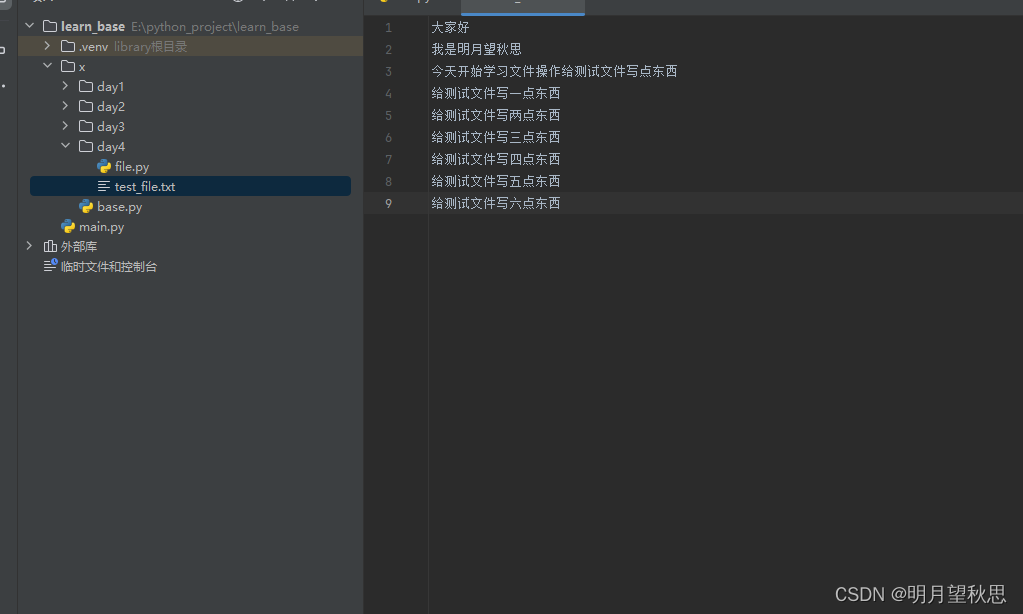
Python学习笔记15:进阶篇(四)文件的读写。
文件操作 学习编程操作中,我觉得文件操作是必不可少的一部分。不管是读书的时候学习的c,c,工作的前学的java,现在学的Python,没学过的php和go,都有文件操作的模块以及库的支持,重要性毫无疑问。…...

角度调制与解调电路
music! (黄佳庆老师可爱捏) 调角 角度调制有较好的抗噪性能。 调相 相位变化的频率变化的微分,频率变化是相位变化的积分 相位的变化率就是频率 调频 调相与调频的关系 大F是输入信号的频率,大Ω是输入信号的角频率 …...
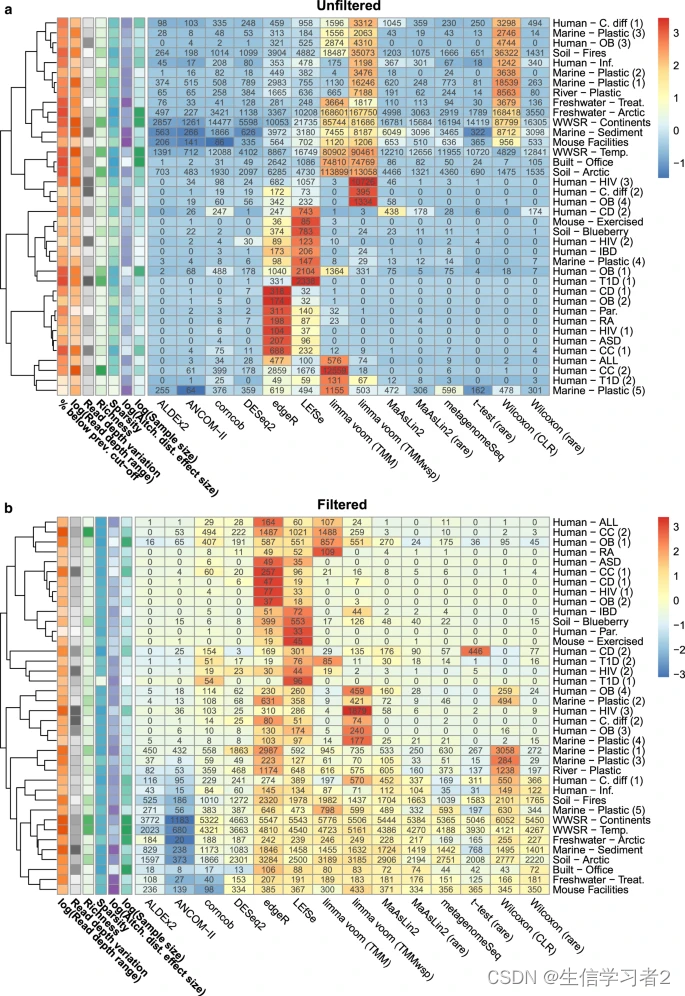
数据分析:微生物组差异丰度方法汇总
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 微生物数据具有一下的特点,这使得在做差异分析的时候需要考虑到更多的问题&…...

Linux驱动开发(二)--字符设备驱动开发提升 LED驱动开发实验
1、地址映射 在编写驱动之前,需要知道MMU,也就是内存管理单元,在老版本的 Linux 中要求处理器必须有 MMU,但是现在Linux 内核已经支持无 MMU 的处理器了。 MMU的功能如下: 完成虚拟空间到物理空间的映射 内存保护&…...
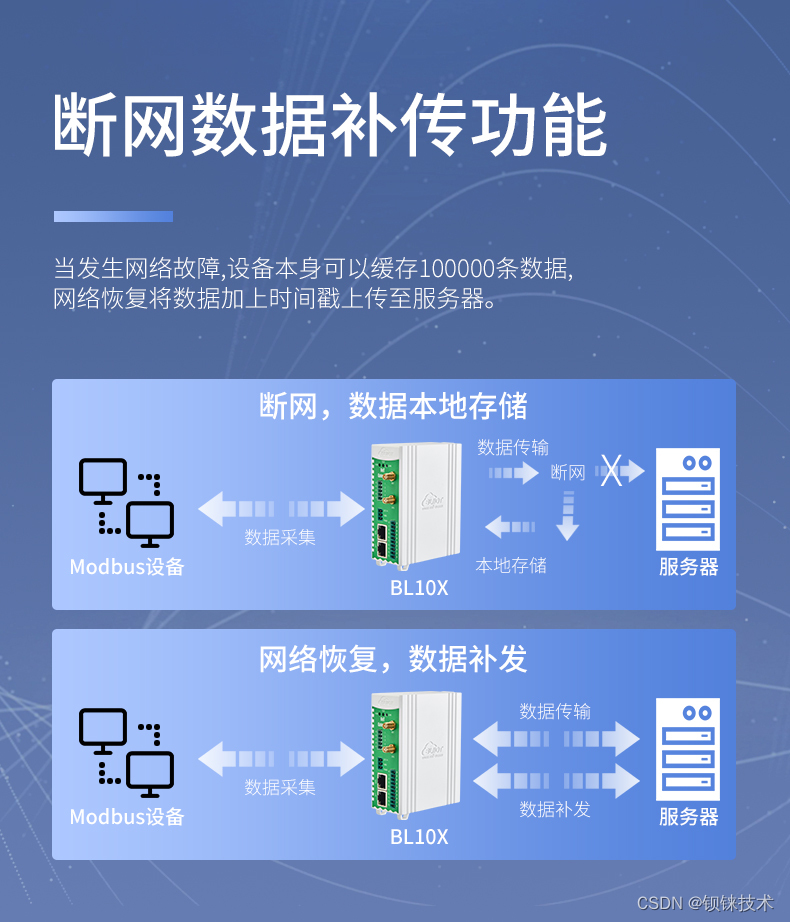
钡铼BL101网关助力智慧城市路灯远程智能管控
在迈向智慧城市的征途中,基础设施的智能化改造是关键一环,而路灯作为城市脉络的照明灯塔,其智能化升级对于节能减排、提升城市管理效率具有重要意义。钡铼BL101网关,作为Modbus转MQTT的专业桥梁,正以其卓越的性能和广泛…...
如何优雅的使用Github Action服务来将Hexo部署到Github Pages
文章目录 参考文章前提条件1. 初始化Hexo2. 初始化仓库3. 创建Token4. 修改_config.yml5. 配置Github Action工作流6. 推送验证7. 配置Github Pages8. 修改Hexo主题样式10. 添加文章遇到了一些问题和方案1. 网站没有样式问题2. 图片不显示 参考文章 Bilibili视频教程-9分钟零成…...

After Effects 2024 mac/win版:创意视效,梦想起航
After Effects 2024是一款引领视效革命的专业软件,汇聚了创意与技术的精华。作为Adobe推出的全新版本,它以其强大的视频处理和动画创作能力,成为从事设计和视频特技的机构,如电视台、动画制作公司、个人后期制作工作室以及多媒体工…...

信息打点web篇----web后端源码专项收集
前言 欢迎来到我的博客 个人主页:北岭敲键盘的荒漠猫-CSDN博客 专栏描述:因为第一遍过信息收集的时候,没怎么把收集做回事 导致后来在实战中,遭遇资产获取少,可渗透点少的痛苦,如今决定 从头来过,全面全方位…...

ArcGIS批量投影转换的妙用(地理坐标系转换为平面坐标系)
点击下方全系列课程学习 点击学习—>ArcGIS全系列实战视频教程——9个单一课程组合系列直播回放 这次文章我们来介绍一下,如何巧妙用要素数据集来实现要素的批量投影。不需要ArcGIS的模型构建器与解决。 例如,有多个要素要将CGCS_2000地理坐标系投…...

YOLOv10训练自己的数据集(图像目标检测)
目录 1、下载代码 2、环境配置 3、准备数据集 4、yolov10训练 可能会出现报错: 1、下载代码 源码地址:https://github.com/THU-MIG/yolov10 2、环境配置 打开源代码,在Terminal中,使用conda 创建虚拟环境配置 命令如下&a…...

解决不能拉取 docker 镜像
# 编辑镜像仓库文件 sudo vi /etc/docker/daemon.json { "registry-mirrors": ["https://registry.docker-cn.com","https://s3d6l2fh.mirror.aliyuncs.com"] }# 重启docker sudo systemctl restart docker参考 https://blog.csdn.net/u01019733…...
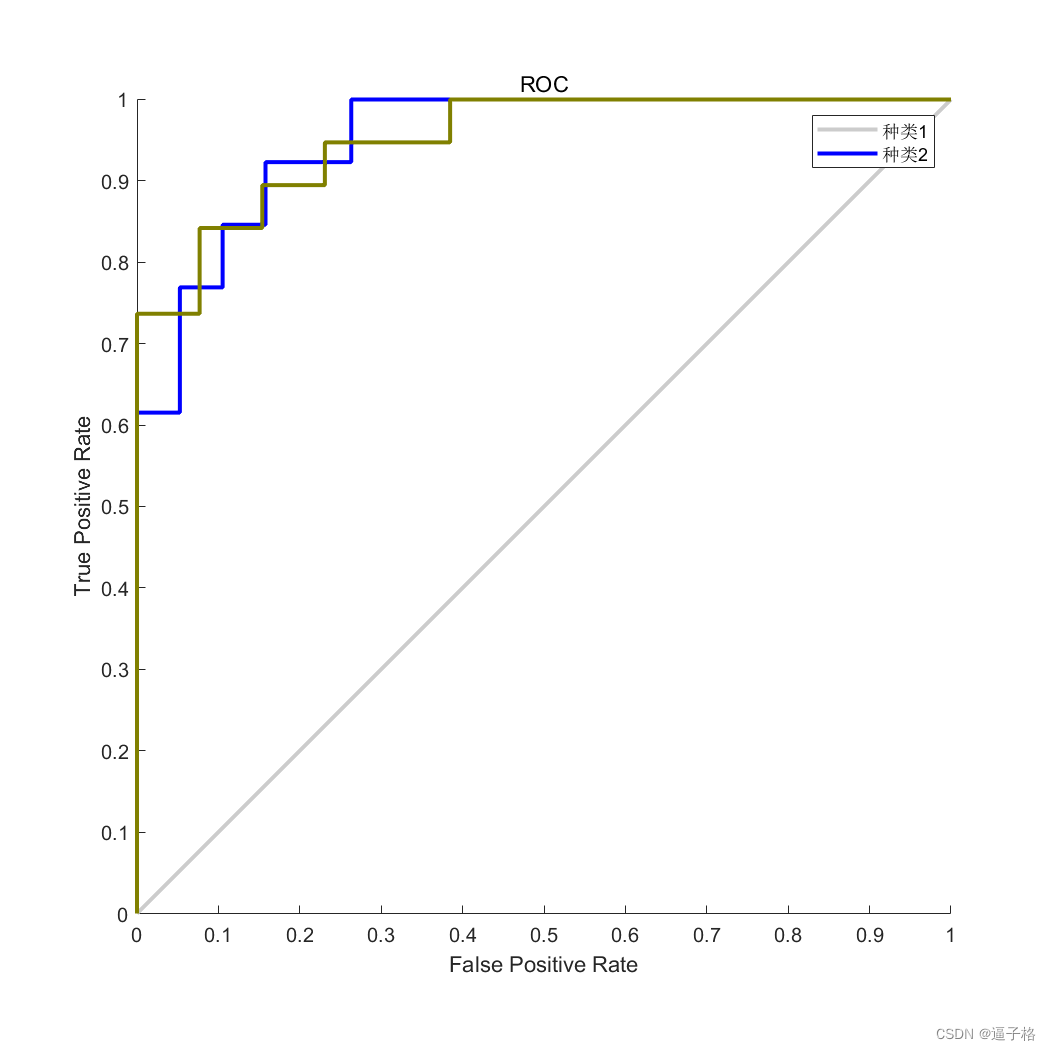
44、基于深度学习的癌症检测(matlab)
1、基于深度学习的癌症检测原理及流程 基于深度学习的癌症检测是利用深度学习算法对医学影像数据进行分析和诊断,以帮助医生准确地检测癌症病变。其原理和流程主要包括以下几个步骤: 数据采集:首先需要收集包括X光片、CT扫描、MRI等医学影像…...

Vue3 【仿 react 的 hook】封装 useTitle
效果预览 页码加载时,自动获取网页标题通过input输入框,可以实时改变网页标题 代码实现 index.vue <template><h1>网页的标题为: {{ titleRef }}</h1><p>通过input输入框实时改变网页的标题 <input v-model"…...

CSS 计数器
CSS 计数器 CSS 计数器是 CSS 中一个强大但经常被忽视的功能。它们允许开发者创建和管理计数器,这些计数器可以在文档中自动递增,非常适合用于编号章节、列表项或其他文档元素。在本文中,我们将深入探讨 CSS 计数器的使用方法、优势和实际应用场景。 CSS 计数器的基本概念…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
