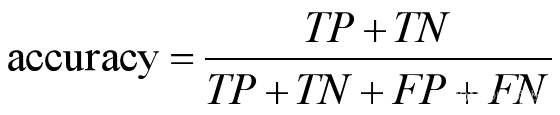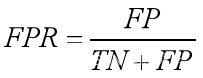【机器学习 复习】第2章 线性回归及最大熵模型
一、概念
1.回归就是用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程称为回归。
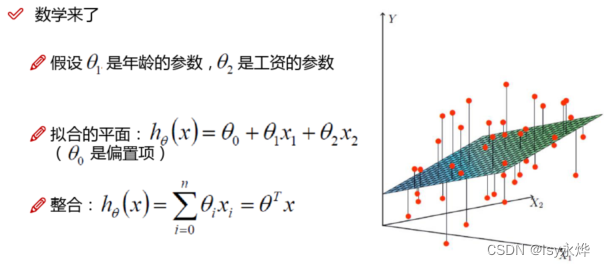
2.一个自变量 叫 一元线性回归,大于一个自变量 叫 多元线性回归。
(1)多元回归:两个x,一个y
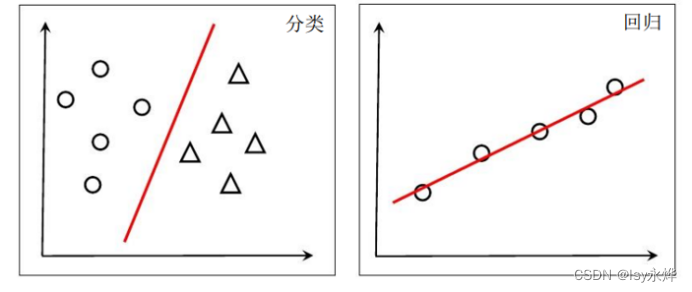
3.这里讲一下线性模型,在二维上就是那根线叫线性模型,他可以用作分类,也可以用作回归:
4. 公式:
(1)准确的说是求 右边的欧米伽和b(用最小二乘法 或者 梯度下降法 求解)。
(2)优化目标:让 【(预测值与真实值之间的欧式距离,下一章)之和】 最小。
预测值就是通过我们用方法推测出的一个点。
真实值就是实际存在的原来样本的一个点,或者说是预测出来本应该是这个点。
5.广义线性模型:
你可以把y替换成lny,原理就跟高中数学里面学的,两边同时取e,最后式子其实是没变化的,这里原理懂了秒懂,不懂得应该也不考无所谓。
6.对率回归 是分类学习算法。其衍生出来的逻辑回归虽然名字中有“回归”,但其主要用途是解决分类问题,特别是二分类问题。
7.梯度下降法简单来说就是一点点求要求的那条直线。
8.人为设置的,而非用来学习的参数,所以叫做超参数。
9.最大熵模型
现实中,不加约束的事物都会朝着“熵增”(不确定,混乱)的方向发展,
当随机变量呈均匀分布时,熵值最大。
最大熵模型就是认为在满足所有约束条件下,熵最大最好(即该情况下数据随机分布,此时最随机,最混乱)。
OK,上面的都不是重点,重点来了:
混淆矩阵
1.基础值缩写:
(1)TN(True negative,真阴率):真0
(2)FN(False nagative,假阴率):假0,即被预测错误的1
(3)TP(True positive,真阳率):真1
(4)FP(False positive,假阳率):假1,即被预测错误的0
2.准确率:表示预测正确的结果占总样本的百分比。
3.精确率(查准率):表示在被预测为正的样本中实际为正的样本的概率。意思就是在预测为正样本的结果中,有多少把握可以预测正确,即不要求对的数量,只要求对的精度/正确率。
4.召回率(查全率):表示在实际为正的样本中被预测为正样本的概率。即是不是所有的1全被找出来了,即要求预测对的数量,但是精度就不保证了。
5.PR曲线:以精确率P为纵坐标,以召回率R为横坐标做出的曲线(竖P横R)。
(1)置信度:(P,R)这样一个点就是置信度
(2)置信度阈值:就是设置一个y轴(P)的值,然后上面的是正例,下面的是负例(上正下负),就是画一条横着的线。
(3)图形:
6.ROC曲线:横轴是假阳率(FPR) 纵轴是真阳率(TPR)
(1)假阳率:
(2)真阳率,就是召回率R:
(3)图形:
(4)x越往右,则表示猜错的正例越来越多,y越往上,则表示猜对的正例越来越多,(1,1)表示此时预测样本全为正例。
二、习题
单选题
7. 逻辑回归模型解决( B)问题
A、回归 B、分类 C、聚类 D、推理
多选题
7. 混淆矩阵大多数评价指标的基础,以下哪些数据它主要包括的信息(ABCD )
A、TN B、TP C、FP D、FN
判断题
6. 逻辑回归是一种广义线性回归,通过回归对数几率的方式将线性回归应用于分类任务。(T)
7. 信息论中,熵可以度量随机变量的不确定性。现实世界中,不加约束的事物都会朝着“熵增”的方向发展,也就是向不确定性增加的方向发展。( T)
8. 准确率可以判断总的正确率,在样本不平衡的情况下,也能作为很好的指标来衡量结果。(F)
相关文章:

【机器学习 复习】第2章 线性回归及最大熵模型
一、概念 1.回归就是用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程称为回归。 2.一个自变量 叫 一元线性回归,大于一个自变量 叫 多元线性回归。 (1)多元回归:两个x,一个…...

关于椭圆的方程(有Python画的动图)
关于椭圆的方程(有Python画的动图) flyfish 几何定义 椭圆是平面上所有到两个固定点(焦点)的距离之和为常数的点的集合。这两个固定点叫做焦点。 解析几何描述 设椭圆的两个焦点为 F 1 F_1 F1 和 F 2 F_2 F2ÿ…...
selenium常见难点解决方案
勾选框勾选问题 勾选框代码逻辑实现过程: 第一步:首先找到勾选框的元素; 第二步:检查它是否已经被勾选。如果已经勾选,则进行取消勾选操作;如果未勾选,则进行点击勾选操作; 以下是一…...

【Python高级编程】 综合练习-使用OpenCV 进行视频数据处理
综合练习 读取一个视频文件,对其进行处理后保存为一个新的视频文件。具体的处理步骤包括调整帧大小、转换为灰度图像、垂直翻转画面以及添加高斯噪声。 下面是代码的详细实现: import cv2 import numpy as np# 定义一个函数,用来给图像添加…...

rs232和can的区别
在电机通讯和升级固件时我们经常用到RS232和CAN两种通讯模式,那这两种有何不同吗? RS232和CAN的主要区别在于通信方式、应用场景、传输距离、通信速度以及网络结构。 通信方式: RS232是一种串行通信接口标准,支持全双工通信&…...

嵌入式软件stm32面试
一、STM32的内核型号有哪些? STM32系列是STMicroelectronics(意法半导体)生产的基于ARM Cortex-M内核的微控制器产品线。这些产品按照不同的内核架构和性能特点分为了主流产品、超低功耗产品和高性能产品。 1.1 主流产品 STM32F0 系列&…...
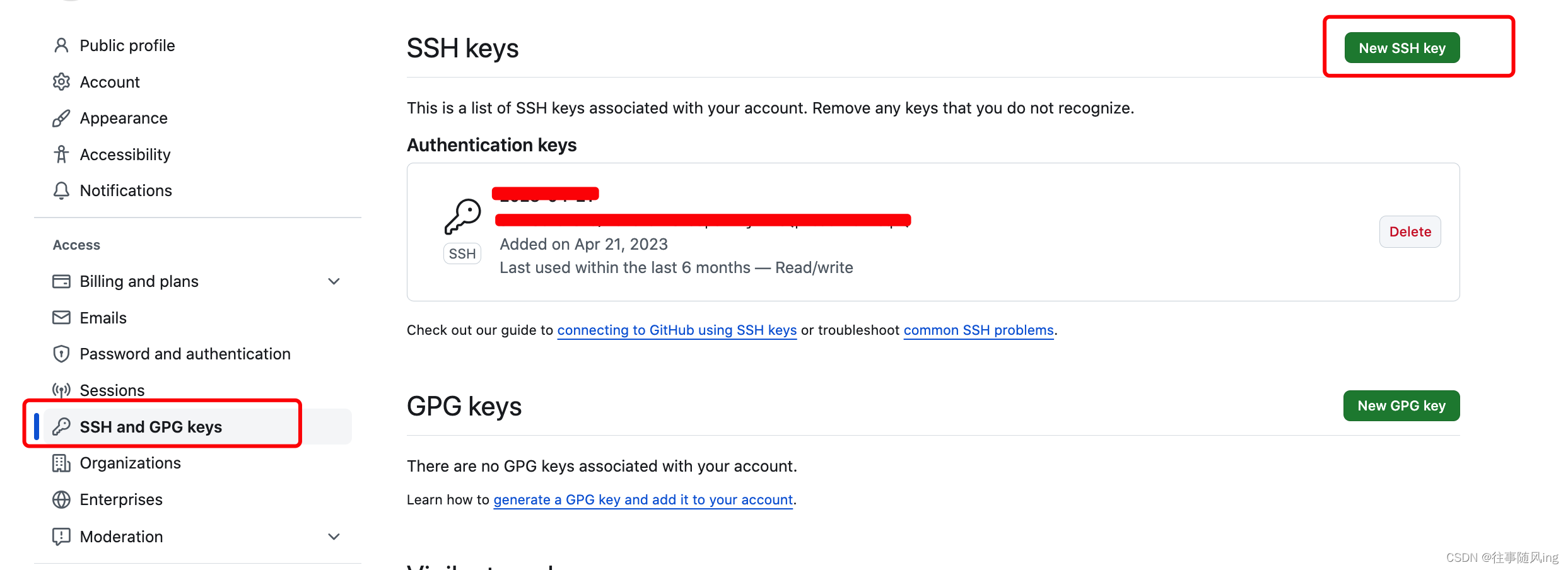
【Git】-- 添加公钥到 github 或者gitlab上
仅针对系统:mac os 、 unix、linux 1、检查是否有 id_rsa.pub $ cd ~ $ ls -al ~/.ssh 注意:若已有 id_rsa.pub,则必要执行 第二步,避免覆盖掉原有正常的公钥。 配置多个 git 账号请参考:同一台电脑配置多个git账…...

Vue页面生成PDF后调起浏览器打印
一、安装依赖 首先,需要安装 html2canvas 和 jsPDF 库。 npm install html2canvas jspdf二、创建公共方法引入 在utils文件夹下创建两个文件分别为pdfExport.js和printPDF.js,代码如下: pdfExport.js import html2canvas from html2canv…...

纯前端实现导出excel
项目背景: vue2 插件: xlsx;xlsx-style;file-saver 说明: 单独使用 xlsx插件,也可以将网页上的table导出成excel,但是导出的excel,没有样式 结合xlsx-style;file-saver&a…...

QT windows 5.12.0 安装包
这个是在线包,需要有账号的。 没有也没事,安装界面可以现场注册 百度网盘链接: 链接:https://pan.baidu.com/s/1QvXDert4b94GbUfD2f2G4g?pwd8888 提取码:8888...

改进YOLOv7 | 在 ELAN 模块中添加【Triplet】【SpatialGroupEnhance】【NAM】【S2】注意力机制 | 附详细结构图
改进 YOLOv7 | 在 ELAN 模块中添加【Triplet】【SpatialGroupEnhance】【NAM】【S2】注意力机制:中文详解 1. 简介 YOLOv7 是目前主流的目标检测算法之一,具有速度快、精度高的特点。但 YOLOv7 的原始模型结构中缺乏注意力机制,导致模型对全…...

windows系统停止更新办法
windows系统停止更新 双击启动下载的文件 然后再回到系统-更新这里,选择日期就行。...

数据标注概念
数据标注的步骤 数据清洗:处理数据中的噪声、缺失值和异常值,确保数据的质量和完整性。 数据转换:将数据从原始格式转换为适合机器学习模型处理的格式。 数据标注:根据应用需求,为数据添加标签或注释,标识…...

网络安全复习笔记
概述 要素 CIA:可用性;完整性;保密性。 可控性;不可否认性;可审查性。 攻击 被动:窃听 - 保密性;监听 - 保密性主动:假冒 - 完整性;重放 - 完整性;改写 -…...
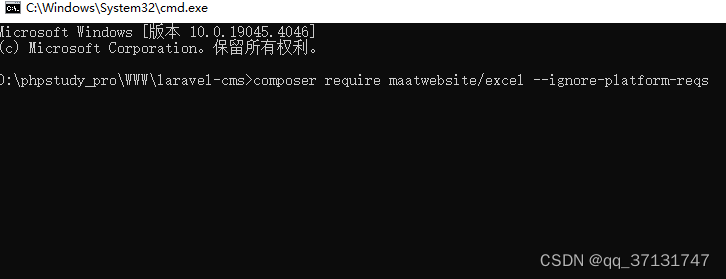
Laravel - excel 导入数据
在Laravel中,可以使用maatwebsite/excel这个库来处理Excel文件的导入。 1.用命令行窗口打开项目根目录,使用 Composer 安装 maatwebsite/excel composer require maatwebsite/excel --ignore-platform-reqs 在你的config/app.php文件中注册服务提供者&…...

移动语义和完美转发
C11 引入了许多新特性,使得编写高效且现代的 C 代码变得更加容易。其中,移动语义(Move Semantics)和完美转发(Perfect Forwarding)是两个重要的特性,极大地提升了 C 的性能和灵活性。 移动语义…...
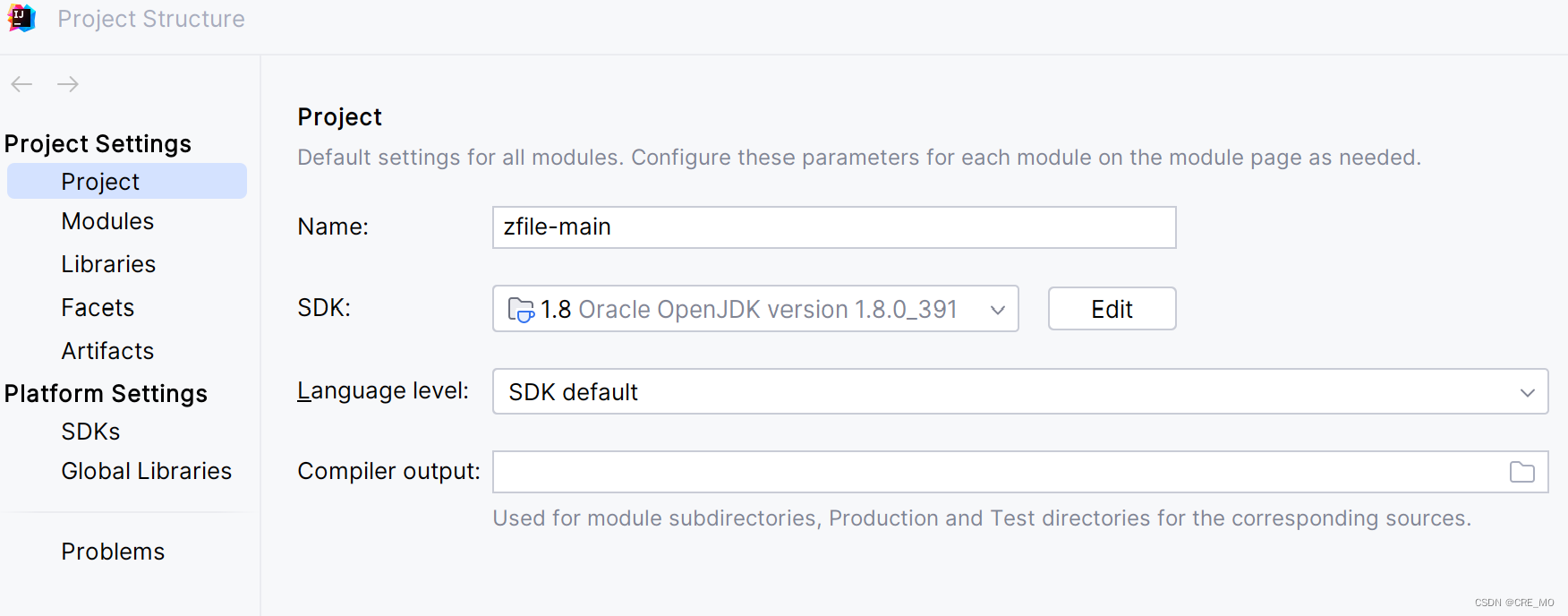
【IDEA】Spring项目build失败
通常因为环境不匹配需要在file->projectstructure里面调整一下。...

【无标题】安卓app 流量
该工具可以用于安卓app 流量,内存,cpu,fps等专项内容测试,并且有整机内存,cpu对比,还可监控手机网速,app流量,数据导出等功能,重点还是免费,毕竟PerfDog收费了…...
国产化ETL产品必备的特性(非开源包装)
ETL负责将分布的、异构数据源中的数据如关系数据、平面数据文件等抽取到临时中间层后进行抽取、清洗(净化)、转换、装载、标准、集成(汇总)...... 最后加载到数据仓库或数据集市中,成为联机分析处理、数据挖掘的基础。…...

flink 操作mongodb的例子
Apache Flink 是一个流处理和批处理的开源框架,它通常用于处理大量数据流。然而,Flink 本身并不直接提供对 MongoDB 的原生支持,因为 MongoDB 是一个 NoSQL 数据库,而 Flink 主要与关系型数据库(如 JDBC 连接器&#x…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...