python实现购物车的功能
模拟购物车,准备一个列表 goodList = [{'name':'笔记本电脑','price':8000}, {'name':'鼠标', 'price':100}]
5个函数 1.加入购物车 2.收藏商品 3.去结算 4.删除购物车商品 5.清空购物车
购物车 cartList = []
收藏列表 collectSet = {'笔记本电脑','鼠标'} 数据示例
去结算计算出总价即可
思路
这是一个购物车程序,主要实现了以下功能:
1. 加入购物车:用户可以选择商品编号,将商品添加到购物车列表中。
2. 收藏商品:用户可以收藏喜欢的商品,收藏的商品会存储在一个集合中。
3. 去结算:计算购物车中商品的总价。
4. 删除购物车商品:用户可以选择要删除的商品编号,将商品从购物车列表中移除。
5. 清空购物车:清空购物车列表中的所有商品。
6. 查看购物车:显示购物车列表中的所有商品。代码首先定义了一个商品列表`goodList`和一个购物车列表`cartList`,以及一个收藏集合`collectSet`。然后通过一个循环,让用户输入操作选项,根据用户的选择执行相应的功能。在每个功能中,都有相应的提示信息和错误处理,以确保程序的正常运行。
'''
# 模拟购物车,准备一个列表 goodList = [{'name':'笔记本电脑','price':8000}, {'name':'鼠标', 'price':100}]
# 5个函数 1.加入购物车 2.收藏商品 3.去结算 4.删除购物车商品 5.清空购物车
# 购物车 cartList = []
# 收藏列表 collectSet = {'笔记本电脑','鼠标'} 数据示例
# 去结算计算出总价即可
'''
goodList = [{'name':'笔记本电脑','price':8000}, {'name':'鼠标', 'price':100}]
print("1.加入购物车 2.收藏商品 3.去结算 4.删除购物车商品 5.清空购物车 6.查看购物车")
cartList = []
collectSet = {'笔记本电脑','鼠标'}
goodList = [{'name': '笔记本电脑', 'price': 8000}, {'name': '鼠标', 'price': 100}]
cartList = []
collectSet = {'笔记本电脑', '鼠标'}
while True:cz = input('请输入你选择的操作')if cz == '1':print('现在的商品有')for i in range(len(goodList)):print(f'{i+1}-商品名称:{goodList[i]["name"]}-商品价格{goodList[i]["price"]}')cart_one = input('请输入你要加入购物车的商品编号: ')selected_index = int(cart_one) - 1if selected_index >= 0 and selected_index < len(goodList):selected_good = goodList[selected_index]cartList.append(selected_good)print(f"已将 {selected_good['name']} 加入购物车")else:print("输入的商品编号无效,请重新输入")if cz == '2':print('现在的商品有')for i in range(len(goodList)):print(f'{i+1}-商品名称:{goodList[i]["name"]}-商品价格{goodList[i]["price"]}')cart_two = input('请输入你想要收藏的商品')for i in range(len(goodList)):if i < len(cart_two):collectSet.add(goodList[i]['name'])print(f"现在收藏有{collectSet}")if cz == '3':print(cartList)cart_sum = sum([i['price'] for i in cartList])print(f"总价{cart_sum}")if cz == '4':print("现在的购物车商品是")for i in range(len(cartList)):print(f'{i + 1}-商品名称:{cartList[i]["name"]}-商品价格{cartList[i]["price"]}')print(f"总价{cart_sum}")cart_four = input('你想要删除的商品编号是')if cart_four.isdigit():cart_four = int(cart_four) - 1if 0 <= cart_four < len(cartList):removed_item = cartList.pop(cart_four)print(f"已将 {removed_item['name']} 删除")else:print("输入的商品编号无效")else:print("请输入有效的数字")if cz == '5':cartList.clear()print("购物车已经清空")if cz == '6':print('现在购物车的商品为')for i in collectSet:print(i)相关文章:

python实现购物车的功能
模拟购物车,准备一个列表 goodList [{name:笔记本电脑,price:8000}, {name:鼠标, price:100}] 5个函数 1.加入购物车 2.收藏商品 3.去结算 4.删除购物车商品 5.清空购物车 购物车 cartList [] 收藏列表 collectSet {笔记本电脑,鼠标} 数据示例 去结算计算出总价…...
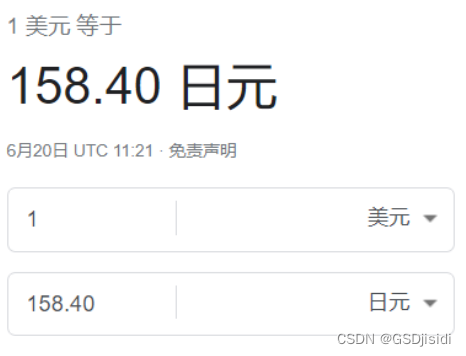
日元预计明年开始上涨
被称为“日元先生”的前大藏省(现财务省)财务官榊原英资预测,美元兑日元汇率将在今年底或2025年初逐步升至130。他认为,通缩时代已经过去,通货膨胀即将来临。 《日本经济新闻》6月5日报道,日本财务省于5月3…...

8、PHP 实现二进制中1的个数、数值的整数次方
题目: 二进制中1的个数 描述: 输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。 <?phpfunction NumberOf1($n) {$count 0;if($n < 0){$n $n & 0x7FFFFFFF;$count;}while($n ! 0){$count;$n $n & ($n - 1…...

linux git凭证管理
linux git 凭证管理 解决命令行git登录github的问题,支持两步验证 同样适用于Azure Devops, Bitbucket 官网: https://github.com/git-ecosystem/git-credential-manager https://github.com/git-ecosystem/git-credential-manager/blob/release/docs/…...

WIC 图像处理初体验——读取像素的值
先放上运行结果: 可以发现红绿蓝是从后往前的。 必须以C方式编译代码! #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <wincodec.h>int main(void) {CoInitialize(nullptr);IWICImagingFactory* fac;CoCreateInstance(CLS…...
,并获取message里面的内容)
使用Server-Sent Events (SSE),并获取message里面的内容
什么是Server-Sent Events (SSE)? Server-Sent Events (SSE)是一种服务器推送技术,允许服务器向客户端(浏览器)发送实时消息。与WebSocket不同,SSE是单向通信,只能从服务器到客户端。SSE在HTML5中作为标准实现&#…...

LabVIEW项目管理中如何平衡成本、时间和质量
在LabVIEW项目管理中,平衡成本、时间和质量是实现项目成功的关键。通过制定详细的项目计划、合理分配资源、严格控制进度、进行质量保证和灵活应对变化,项目管理者可以有效地协调这三者的关系,确保项目按时、按质、按预算完成。 1. 制定详细…...

如何检查 Kubernetes 网络配置
简介 Kubernetes 是一个容器编排系统,可以管理集群中的容器化应用程序。在集群中保持所有容器之间的网络连接需要一些高级网络技术。在本文中,我们将简要介绍一些工具和技术,用于检查这种网络设置。 如果您正在调试连接问题,调查…...

如何将网站封装成App:小猪APP分发助你实现
你有没有想过,将你的网站变成一个App会是什么样子?想象一下,用户只需点击一下图标,就能立刻访问你的内容,而不是在浏览器中输入网址。这不仅提升了用户体验,还能增加用户粘性。这一切都可以通过将网站封装成…...

探索C嘎嘎的奇妙世界:第十六关---STL(vector的练习)
1.只出现一次的数字 我们可以使用异或运算来解决这个问题: 异或运算有一个重要的性质:两个相同的数进行异或运算结果为 0,任何数与 0 异或结果为其本身。对于数组中的元素,依次进行异或运算,出现两次的元素异…...

最新扣子(Coze)实战案例:扣子卡片的制作及使用,完全免费教程
🧙♂️ 大家好,我是斜杠君,手把手教你搭建扣子AI应用。 📜 本教程是《AI应用开发系列教程之扣子(Coze)实战教程》,完全免费学习。 👀 关注斜杠君,可获取完整版教程。👍Ἷ…...

Node-red win11安装
文章目录 前言一、安装node.js和npm二、安装Node-red三、 运行Node-red 前言 Node-RED 是一种编程工具,用于以新颖有趣的方式将硬件设备、API 和在线服务连接在一起。 它提供了一个基于浏览器的编辑器,只需单击一下即可将调色板中的各种节点轻松连接在…...

永久更改R包的安装目录
要永久更改 R 包的安装目录,可以通过设置 R 配置文件来实现。以下是步骤说明: 1. 查找和修改 R 配置文件 R 有几个配置文件用于保存用户和系统的设置: 用户级配置文件:通常位于 ~/.Rprofile系统级配置文件:通常位于…...
)
Webrtc支持FFMPEG硬解码之NVIDA(二)
一、前言 此系列文章分分为三篇, Webrtc支持FFMPEG硬解码之Intel(一)-CSDN博客 Webrtc支持FFMPEG硬解码之NVIDA(二)-CSDN博客 Webrtc支持FFMPEG硬解码之解码实现-CSDN博客 AMD硬解目前还没找到可用解码器,欢迎留言交流 二、环境 Windows平台 VS2019 Cmake 三、下…...
)
整理好了!2024年最常见 20 道设计模式面试题(九)
上一篇地址:整理好了!2024年最常见 20 道设计模式面试题(八)-CSDN博客 十七、什么是享元模式?它在资源优化中扮演什么角色? 享元模式(Flyweight Pattern)是一种常用的软件设计模式…...

RAG实操教程langchain+Milvus向量数据库创建你的本地知识库 二
Miluvs 向量数据库 关于 Milvui 可以参考我的前两篇文章 • 一篇文章带你学会向量数据库Milvus(一)[1]• 一篇文章带你学会向量数据库Milvus(二)[2] 下面我们安装 pymilvus 库 pip install --upgrade --quiet pymilvus如果你…...
Spring+SpringMVC介绍+bean实例化+依赖注入实战
Spring介绍 Spring是一个轻量级的Java 开发框架,核心是IOC(控制反转)和AOP(面向切面编程) Spring解决了业务层(Service包)与其他各层(表现层,包括Model,Vie…...
【安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录】
安装笔记-系列文章目录 安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录 文章目录 安装笔记-系列文章目录安装笔记-20240616-Linux-为 OpenWrt 自动挂载 Windows 主机共享目录 前言一、软件介绍名称:cifsutils主页官方介绍特点 二、安装步骤测试…...

61.WEB渗透测试-信息收集- WAF、框架组件识别(1)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:60.WEB渗透测试-信息收集- 端口、目录扫描、源码泄露(8) WAF的识…...

qmt量化交易策略小白学习笔记第45期【qmt编程之期货行情数据--如何获取日线行情、tick行情】
qmt编程之获取期货行情数据 qmt更加详细的教程方法,会持续慢慢梳理。 也可找寻博主的历史文章,搜索关键词查看解决方案 ! 感谢关注,咨询免费开通量化回测与获取实盘权限,欢迎和博主联系! 获取日线行情数…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
