从二元一次方程组到二阶行列式再到克拉默法则
目录
- 引言
- 1 二元一次方程组
- 什么是二元一次方程组?
- 解法概述
- 示例
- 1. 操作步骤
- 2. 消元法
- 2 二阶行列式
- 引入行列式
- 行列式定义
- 示例计算
- 3 克拉默法则
- 什么是克拉默法则?
- 克拉默法则公式
- 使用克拉默法则求解
- 4 总结
引言
在数学中,线性代数提供了一套强大的工具来解决各种实际问题。本文将介绍从二元一次方程组开始,如何利用二阶行列式和克拉默法则来求解问题。
1 二元一次方程组
什么是二元一次方程组?
二元一次方程组指包含两个变量的一次方程组,通常形如:
{ 3 x + 4 y = 5 7 x + 9 y = 11 \begin{cases} 3x + 4y = 5 \\ 7x + 9y = 11 \end{cases} {3x+4y=57x+9y=11
这里,3、4、7、9、5 和 11 是已知的常数,(x) 和 (y) 是需要求解的未知数。
解法概述
解决这种方程组的一种基本方法是消元法。通过适当的操作消去一个变量,简化成一个关于单个变量的方程。让我们详细说明这个过程。
示例
1. 操作步骤
首先,我们将两个方程进行变形,以便消去一个变量。
原方程组:
{ 3 x + 4 y = 5 7 x + 9 y = 11 \begin{cases} 3x + 4y = 5 \\ 7x + 9y = 11 \end{cases} {3x+4y=57x+9y=11
2. 消元法
为了消去一个变量,我们将第一个方程和第二个方程进行适当的变换。假设我们希望消去 (x),我们可以进行如下操作:
将第一个方程乘以 7:
将第二个方程乘以 3:
{ 7 ⋅ 3 x + 7 ⋅ 4 y = 7 ⋅ 5 3 ⋅ 7 x + 3 ⋅ 9 y = 3 ⋅ 11 \begin{cases} 7 \cdot 3x + 7 \cdot 4y = 7 \cdot 5 \\ 3 \cdot 7x + 3 \cdot 9y = 3 \cdot 11 \end{cases} {7⋅3x+7⋅4y=7⋅53⋅7x+3⋅9y=3⋅11
两式相减,求得 y 的值
y = 7 ⋅ 5 − 3 ⋅ 11 7 ⋅ 4 − 3 ⋅ 9 y=\frac{7 \cdot 5 - 3 \cdot 11}{7 \cdot 4 - 3 \cdot 9} y=7⋅4−3⋅97⋅5−3⋅11
现在我们就想,把分子分母换成行列式写法,由此就引入了二阶行列式的写法,上面的式子可以写为这样
y = ∣ 7 3 11 5 ∣ ∣ 7 3 9 4 ∣ y = \frac{\begin{vmatrix} 7 & 3 \\ 11 & 5 \end{vmatrix}}{\begin{vmatrix} 7 & 3 \\ 9 & 4 \end{vmatrix}} y= 7934 71135
最后求得 x 和 y 的值:
y = 2 x = − 1 y = 2 \\ x = -1 y=2x=−1
2 二阶行列式
引入行列式
在上面的步骤中,我们进行了方程变换和变量消去,实际上可以使用行列式的方法来简化这些步骤。
行列式定义
行列式是一种代数表达式,用于求解线性方程组。二阶行列式定义如下:
∣ a b c d ∣ = a d − b c \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc acbd =ad−bc
示例计算
对于矩阵
( 3 4 7 9 ) \begin{pmatrix} 3 & 4 \\ 7 & 9 \end{pmatrix} (3749)
其行列式为:
∣ 3 4 7 9 ∣ = 3 ⋅ 9 − 4 ⋅ 7 = 27 − 28 = − 1 \begin{vmatrix} 3 & 4 \\ 7 & 9 \end{vmatrix} = 3 \cdot 9 - 4 \cdot 7 = 27 - 28 = -1 3749 =3⋅9−4⋅7=27−28=−1
3 克拉默法则
什么是克拉默法则?
克拉默法则是一种利用行列式解决线性方程组的方法。对于一个二元一次方程组:
{ 3 x + 4 y = 5 7 x + 9 y = 11 \begin{cases} 3x + 4y = 5 \\ 7x + 9y = 11 \end{cases} {3x+4y=57x+9y=11
它可以表示成矩阵形式 (AX = B),其中:
A = ( 3 4 7 9 ) , X = ( x y ) , B = ( 5 11 ) A = \begin{pmatrix} 3 & 4 \\ 7 & 9 \end{pmatrix}, X = \begin{pmatrix} x \\ y \end{pmatrix}, B = \begin{pmatrix} 5 \\ 11 \end{pmatrix} A=(3749),X=(xy),B=(511)
克拉默法则公式
克拉默法则提供了求解线性方程组的公式。可以很方便的解出 (x) 和 (y),注意分母都是一样的:
x = ∣ 5 4 11 9 ∣ ∣ 3 4 7 9 ∣ , y = ∣ 3 5 7 11 ∣ ∣ 3 4 7 9 ∣ x = \frac{\begin{vmatrix} 5 & 4 \\ 11 & 9 \end{vmatrix}}{\begin{vmatrix} 3 & 4 \\ 7 & 9 \end{vmatrix}}, \quad y = \frac{\begin{vmatrix} 3 & 5 \\ 7 & 11 \end{vmatrix}}{\begin{vmatrix} 3 & 4 \\ 7 & 9 \end{vmatrix}} x= 3749 51149 ,y= 3749 37511
使用克拉默法则求解
- 计算分母:
∣ 3 4 7 9 ∣ = 3 ⋅ 9 − 4 ⋅ 7 = − 1 \begin{vmatrix} 3 & 4 \\ 7 & 9 \end{vmatrix} = 3 \cdot 9 - 4 \cdot 7 = -1 3749 =3⋅9−4⋅7=−1
- 计算 (x) 的分子:
∣ 5 4 11 9 ∣ = 5 ⋅ 9 − 4 ⋅ 11 = 45 − 44 = 1 \begin{vmatrix} 5 & 4 \\ 11 & 9 \end{vmatrix} = 5 \cdot 9 - 4 \cdot 11 = 45 - 44 = 1 51149 =5⋅9−4⋅11=45−44=1
- 计算 (y) 的分子:
∣ 3 5 7 11 ∣ = 3 ⋅ 11 − 5 ⋅ 7 = 33 − 35 = − 2 \begin{vmatrix} 3 & 5 \\ 7 & 11 \end{vmatrix} = 3 \cdot 11 - 5 \cdot 7 = 33 - 35 = -2 37511 =3⋅11−5⋅7=33−35=−2
- 求解:
x = 1 − 1 = − 1 x = \frac{1}{-1} = -1 x=−11=−1
y = − 2 − 1 = 2 y = \frac{-2}{-1} = 2 y=−1−2=2
4 总结
本文我们从二元一次方程组的基本求解方法开始,逐步引入了行列式,并最终介绍了克拉默法则。在实际应用中,使用行列式和克拉默法则可以简化计算过程,使得解决线性方程组更加直观和有效。
相关文章:

从二元一次方程组到二阶行列式再到克拉默法则
目录 引言1 二元一次方程组什么是二元一次方程组?解法概述示例1. 操作步骤2. 消元法 2 二阶行列式引入行列式行列式定义示例计算 3 克拉默法则什么是克拉默法则?克拉默法则公式使用克拉默法则求解 4 总结 引言 在数学中,线性代数提供了一套强…...
示例:WPF中绑定枚举到ComboBox想显示成中文或自定义名称如何实现
一、目的:在开发过程中绑定的枚举不想显示成英文字段怎么办,这里通过TypeConverter的方式来实现绑定的枚举从定义的特性中读取 二、实现 首先定义如下枚举 [TypeConverter(typeof(DisplayEnumConverter))]public enum MyEnum{[Display(Name "无&q…...

嵌入式系统软件架构设计方法
1.嵌入式系统软件架构设计的目的 嵌入式系统软件架构是开发大型嵌入式系统密集型软件贯穿始终的关键桥梁,同时软件架构也是软件开发的基础。架构设计的目的是: 保证应用的代码逻辑清晰,避免重复的设计;实现软件的可移植性&#…...
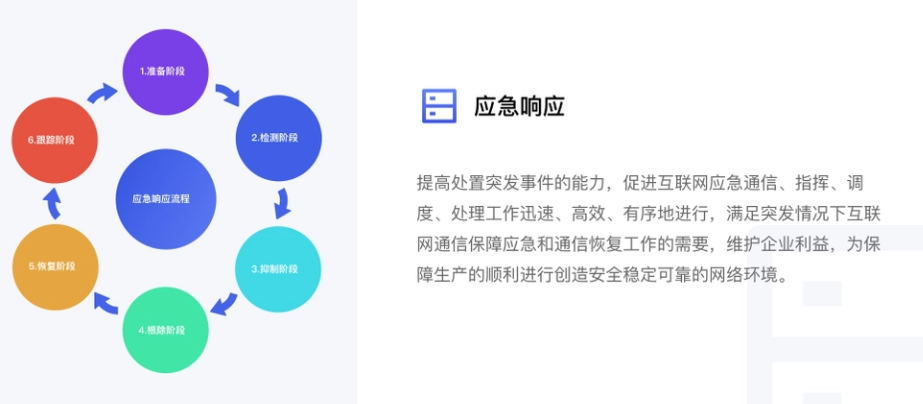
【面试题】风险评估和应急响应的工作流程
风险评估和应急响应是网络安全管理中两个重要的环节。下面分别介绍它们的工作流程: 一、风险评估工作流程: 1.确定评估范围:明确需要评估的信息系统或资产的范围。 2.资产识别:识别并列出所有需要评估的资产,包括硬件…...

Vue70-路由的几个注意点
一、路由组件和一般组件 1-1、一般组件 1-2、路由组件 不用写组件标签。靠路由规则匹配出来,由路由器渲染出来的组件。 1-3、注意点1 一般组件和路由组件,一般放在不同的文件夹,便于管理。 一般组件放在components文件夹下。 1-4、注意点…...
Aidlux 1.4 部署Nextcloud 2024.6实录 没成功
Aidux阉割版Debain10,坑很多,比如找不到实际的系统日志,有知道的大神吗? 1 Apache2安装 # 测试Apache2 sudo apt update && sudo apt upgrade sudo apt install apache2 -y80端口疑似被禁止只能换端口 rootlocalhost:/…...

网络与协议安全复习 - 电子邮件安全
文章目录 PGP(Pretty Good Privacy)功能 S/MIME(Secure/Multipurpose Internet Mail Extensions)DKIM(Domain Keys Identified Mail) PGP(Pretty Good Privacy) 使用符号: Ks:会话密钥、KRa:A 的私钥、KUa:A 的公钥、EPÿ…...

Python里的序列化是什么?
在Python中,序列化(serialization)是一个过程,它可以将数据结构或对象状态转换为可以存储或传输的形式。通常,这意味着将数据结构或对象转换为字节流,以便可以将其写入文件、发送到网络,或用于其…...

自动抓取服务器功耗
以下脚本为linux系统内通过ipmitool工具自动抓取服务器当前功耗,每隔5分钟抓取一次,累计抓取20次 脚本如下: #!/bin/bashcurrent_dirpwd node_list${current_dir}/nodelistbmc #BMC IP usernameAdministrator #BMC用…...

服务器接收苹果订阅通知
我们的服务器需要提供一个URL来接收苹果的通知,要使用HTTPS。 苹果会对这个URL发送HTTP POST请求,body是JSON格式,包含了通知的内容。 我们服务器处理成功后,应向苹果返回HTTP 200。若出现问题,需要苹果重新发送通知…...

2024年旅游与经济发展国际会议(ICTED 2024)
2024年旅游与经济发展国际会议(ICTED 2024) 2024 International Conference on Tourism and Economic Development 【重要信息】 大会地点:青岛 大会官网:http://www.icicted.com 投稿邮箱:icictedsub-conf.com 【注意…...
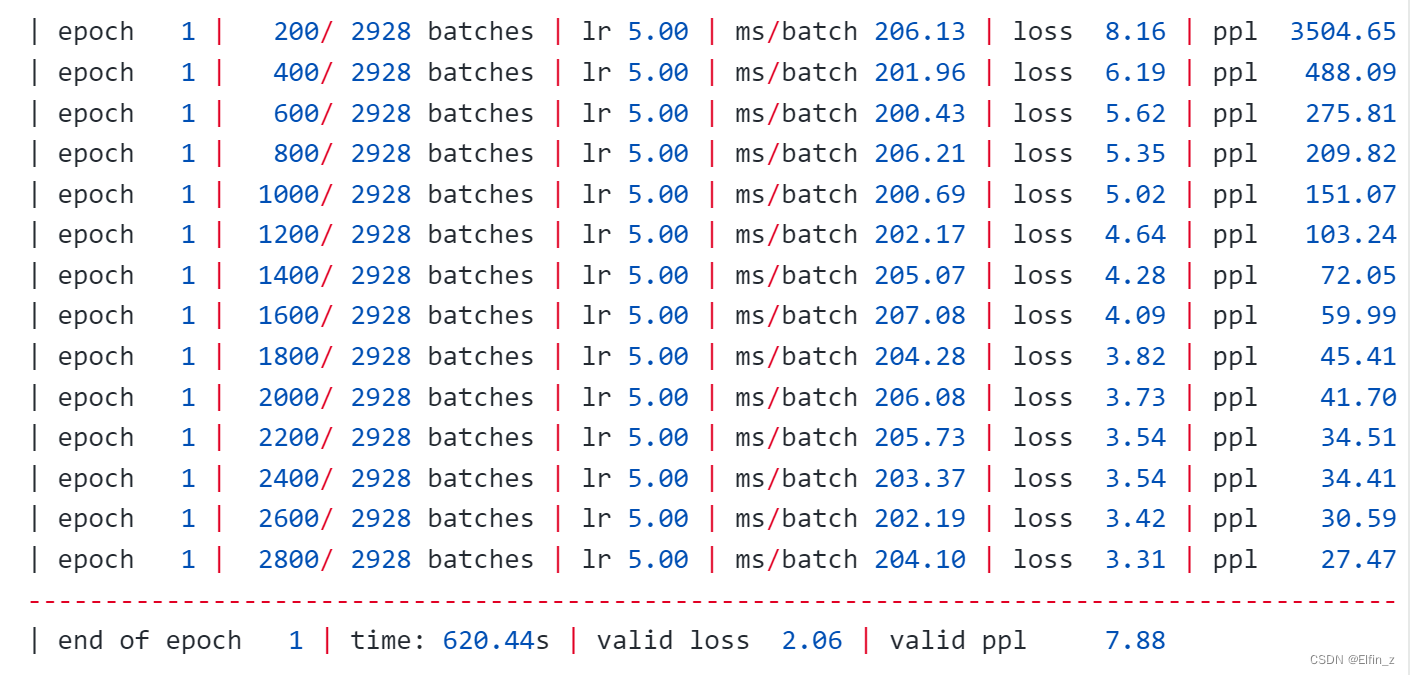
【NLP练习】Transformer实战-单词预测
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 任务:自定义输入一段英文文本进行预测 一、定义模型 from tempfile import TemporaryDirectory from typing import Tuple from torch import nn…...

使用Lua脚本保证原子性的Redis分布式锁实现
这是原来的代码: Override public void unlock() {// 获取线程标示String threadId ID_PREFIX Thread.currentThread().getId();// 判断标示是否一致String id stringRedisTemplate.opsForValue().get(KEY_PREFIX name);if (threadId.equals(id)) {// 释放锁st…...

什么是nginx到底怎么配置,什么是网关到底怎么配置?
那使用upstream里面具体哪个服务器是怎么决定和区分的呢? AI生成 在Nginx中,使用upstream里面具体哪个服务器是通过负载均衡算法来决定的。upstream块定义了一组服务器,Nginx会根据配置的负载均衡算法来选择一个服务器来处理当前的请求。常见的负载均衡算法包括轮询(round-…...
)
轻量级服务器内存不够编译的情况解决方案(以安装Ta-Lib库为例)
安装 TA-Lib 时遇到的问题通常与系统缺少必要的编译依赖项或者内存不足有关。以下是一些解决步骤,你可以按照这些步骤尝试解决问题: 问题描述:编译安装Tal-ib库出现以下问题: root@tianbaobao12:~/shipan/ta-lib# pip install ta-lib Collecting ta-libUsing cached TA-L…...

学校校园考场电子钟,同步授时,助力考场公平公正-讯鹏科技
随着教育技术的不断发展,学校对于考场管理的需求也日益提高。传统的考场时钟往往存在时间误差、维护不便等问题,这在一定程度上影响了考试的公平性和公正性。为了解决这些问题,越来越多的学校开始引入考场电子钟,通过同步授时技术…...
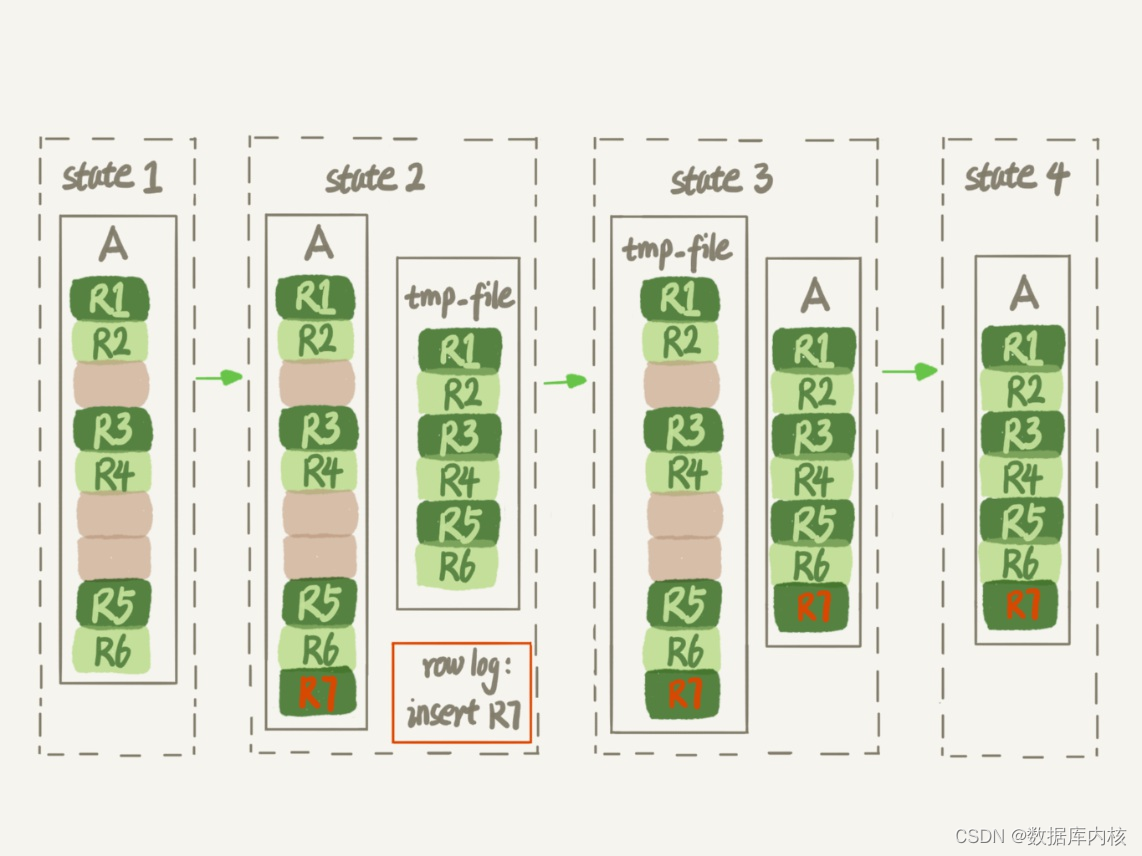
MySQL存储管理(一):删数据
从表中删除数据 从表中删除数据,也即是delete过程。 什么是表空间 表空间可以看做是InnoDB存储引擎逻辑结构的最高层,所有的数据都存放在表空间中。默认情况下,InnoDB存储引擎有一个共享表空间idbdata1,即所有数据都存放在这个表…...

深度剖析现阶段的多模态大模型做不了医疗
导读 在人工智能的这波浪潮中,以ChatGPT为首的大语言模型(LLM)不仅在自然语言处理(NLP)领域掀起了一场技术革命,更是在计算机视觉(CV)乃至多模态领域展现出了令人瞩目的潜力。 这些…...
Zabbix 监控 Kubernetes 集群
Zabbix 监控 Kubernetes 集群 Zabbix作为一个成熟且功能强大的监控系统,被许多企业广泛采用。它能够对各种IT基础设施进行全面的监控,包括服务器、网络设备、应用程序等。而将Zabbix与Kubernetes结合,可以实现对Kubernetes集群的全面监控&am…...

网上预约就医取号系统
摘 要 近年来,随着信息技术的发展和普及,我国医疗信息产业快速发展,各大医院陆续推出自己的信息系统来实现医疗服务的现代化转型。不可否认,对一些大型三级医院来说,其信息服务质量还是广泛被大众所认可的。这就更需要…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
