矩阵中严格递增的单元格数
题目链接:leetcode:矩阵中严格递增的单元格数
描述
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
其中:
m == mat.length
n == mat[i].length
1 <= m, n <= 10^5
1 <= m * n <= 10^5
-10^5 <= mat[i][j] <= 10^5
输入
mat = [[3,1,6],[-9,5,7]]
输出
4
PS:之前有事漏做了ε=(´ο`*)))唉,今天补一下。
思路:
初看题目,位置(i, j),只能移动到同行或同列中值严格比他大的位置。因此可以将这个矩阵根据每个位置间的可到达性建立一张拓扑图,所求的得到最大单元格访问数量的路线,必然是从拓扑图中某一个入度为0的位置出发到某一个出度为0的位置结束。根据这个特性,我们可以从入度为0或者出度为0的位置出发来计算最大单元格访问数量。
在这里我采用了从出度为0出发的思路,个人感觉更“顺”一点。
设从位置(i , j)出发的最大单元格访问数为dp[i][j],(i, p)可表示所有同行中(i, j)可到达的位置,(q, j)可表示同列中(i , j)可到达的位置。那么dp[i][j] = max(max(dp[i][p]+1), max(dp[q][j]+1) ) 。从这里可以看出,要得到dp[i][j],我们要算出同行中所有的dp[i][p]和同列中所有的dp[q][j],所以我们要从拓扑图的右边往左边计算dp[i][j](最右边位置出度为0,dp[i][j] = 1)。
如果能顺利建图,那么问题就简单了,但是这里矩阵可能出现一维的情况,那么建图的复杂度就为O(n^2),对于n最大为1e5的情况显然会超时,所以还得优化思路。
不能建图,那就继续从小的只能往大的位置走这一特性入手,并从整体出发。只要我先计算了所有比位置(i, j)值大的位置的dp值,那么计算dp[i][j]所需的依赖——dp[i][p]和dp[q][j],都已经算好了。现在有了dp[i][p]和dp[q][j],就剩下max(dp[i][p])和max(dp[q][j])的计算。若每次都采用遍历的方法去计算max(dp[i][p])和max(dp[q][j]),总复杂度又回到了O(n^2),仍需优化。
以max(dp[i][p])的计算为例,若有两个位置(i, j0)和(i, j1), 且mat[i][j0] = mat[i][j1] + 1(只要mat[i][j1]是第i行中仅次于mat[i][j0]的值就行了),目前已知dp[i][j0],那么(i, j1)的max(dp[i][p]) = dp[i][j0] + 1。因此我们可建立两个数组,一个保存每行的最大dp值,一个保存每列的最大dp值。虽然我们是按mat值从大到小计算dp值,能保证不少算东西,但行或列中可能会存在相同的值,会多算东西。所以对于每行/每列的最大dp值需要存两个,一个存最大dp值一个存次大dp值,且取得两个值所在位置的mat值不能相同。这样就只需要在计算时比较一下mat[i][j]是否等于最大值所在mat值就行了,若不等于则选择最大dp值,反之选次大dp值。
struct node
{int val, x, y;bool operator < (const node &o)const{return val > o.val;}
};
struct dpnode
{int val_0, cnt_0;int val_1, cnt_1;void update(int val, int cnt){if(val == val_0){if(cnt > cnt_0){cnt_0 = cnt;}}else {if(cnt > cnt_0){cnt_1 = cnt_0;val_1 = val_0;cnt_0 = cnt;val_0 = val;}else if(cnt > cnt_1){cnt_1 = cnt;val_1 = val;}}}
};
const int inf = -1e5 - 5;
class Solution {
public:int maxIncreasingCells(vector<vector<int>>& mat) {int n = mat.size(), m = mat[0].size();vector<node> arr(n * m);dpnode demoe = (dpnode){inf, 0, inf, 0};vector<dpnode> row(n, demoe), col(m, demoe);for(int i = 0; i < n;i++){for(int j = 0;j < m;j++){arr[i*m+j] = (node){mat[i][j], i, j};}} sort(arr.begin(), arr.end());int ans=0;int tmp_row, tmp_col;for(int i = 0;i < arr.size();i++){if(row[arr[i].x].val_0 != arr[i].val){tmp_row = row[arr[i].x].cnt_0 + 1;}else tmp_row = row[arr[i].x].cnt_1 + 1;if(col[arr[i].y].val_0 != arr[i].val){tmp_col = col[arr[i].y].cnt_0 + 1;}else tmp_col = col[arr[i].y].cnt_1 + 1;if(tmp_col > tmp_row) tmp_row = tmp_col;row[arr[i].x].update(arr[i].val, tmp_row);col[arr[i].y].update(arr[i].val, tmp_row);}for(int i = 0;i < n;i++){ans = max(ans, row[i].cnt_0);}for(int j = 0;j < m;j++){ans = max(ans, col[j].cnt_0);}return ans;}
};
若有什么错误,欢迎指正^ _ ^ 。
相关文章:

矩阵中严格递增的单元格数
题目链接:leetcode:矩阵中严格递增的单元格数 描述 给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。 从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目…...
)
超参数调优-通用深度学习篇(上)
文章目录 深度学习超参数调优网格搜索示例一:网格搜索回归模型超参数示例二:Keras网格搜索 随机搜索贝叶斯搜索 超参数调优框架Optuna深度学习超参数优化框架nvidia nemo大模型超参数优化框架 参数调整理论: 黑盒优化:超参数优化…...

小程序中data-xx是用方式
data-sts"3" 是微信小程序中的一种数据绑定语法,用于在 WXML(小程序模板)中将自定义的数据绑定到页面元素上。让我详细解释一下: data-xx 的作用: data-xx 允许你在页面元素上自定义属性,以便在事…...

【2024德国工作】外国人在德国找工作是什么体验?
挺难的,德语应该是所有中国人的难点。大部分中国人进德国公司要么是做中国业务相关,要么是做技术领域的工程师。先讲讲人在中国怎么找德国的工作,顺便延申下,德国工作的真实体验,最后聊聊在今年的德国工作签证申请条件…...

Unity中获取数据的方法
Input和GetComponent 一、Input 1、Input类: 用于处理用户输入(如键盘、鼠标、触摸等)的静态类 2、作用: 允许你检查用户的输入状态。如某个键是否被按下,鼠标的位置,触摸的坐标等 3、实例 (1) 键盘…...

Java的死锁问题
Java中的死锁问题是指两个或多个线程互相持有对方所需的资源,导致它们在等待对方释放资源时永久地阻塞的情况。 死锁产生条件 死锁发生通常需要满足以下四个必要条件: 互斥条件:至少有一个资源是只能被一个线程持有的,如果其他…...

Unity 公用函数整理【二】
1、在规定时间时间内将一个值变化到另一个值,使用Mathf.Lerp实现 private float timer;[Tooltip("当前温度")]private float curTemp;[Tooltip("开始温度")]private float startTemp 20;private float maxTemp 100;/// <summary>/// 升…...

千年古城的味蕾传奇-平凉锅盔
在甘肃平凉这片古老而神秘的土地上,有一种美食历经岁月的洗礼,依然散发着独特的魅力,那便是平凉锅盔。平凉锅盔,那可是甘肃平凉的一张美食名片。它外表金黄,厚实饱满,就像一轮散发着诱人香气的金黄月亮。甘…...
微信小程序视频如何下载
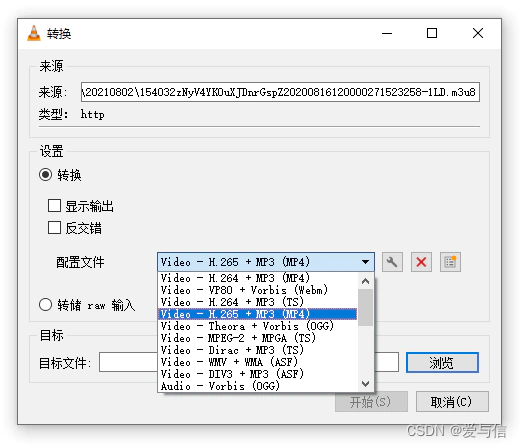
一、工具准备 1、抓包工具Fiddler Download Fiddler Web Debugging Tool for Free by Telerik 2、VLC media player Download official VLC media player for Windows - VideoLAN 3、微信PC端 微信 Windows 版 二、开始抓包 1、打开Fiddler工具,设置修改如下…...

SVN 安装教程
SVN 安装教程 SVN(Subversion)是一个开源的版本控制系统,广泛用于软件开发和文档管理。本文将详细介绍如何在不同的操作系统上安装SVN,包括Windows、macOS和Linux。 Windows系统上的SVN安装 1. 下载SVN 访问SVN官方网站或Visu…...

HTML静态网页成品作业(HTML+CSS)—— 家乡山西介绍网页(3个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有6个页面。 二、作品演示 三、代…...
:定理6的补充证明及三道循环置换例题)
【抽代复习笔记】20-群(十四):定理6的补充证明及三道循环置换例题
例1:找出S3中所有不能和(123)交换的元。 解:因为 (123)(1) (1)(123) (123),(123)(132) (132)(123) (1),所以(1)、(132)和(123)均可以交换; 而(12)(123) (23),(123)(12) (13),故 (12)(12…...
【单片机毕业设计选题24018】-基于STM32和阿里云的农业大棚系统
系统功能: 系统分为手动和自动模式,上电默认为自动模式,自动模式下系统根据采集到的传感器值 自动控制,温度过低后自动开启加热,湿度过高后自动开启通风,光照过低后自动开启补 光,水位过低后自动开启水泵…...

【计算机毕业设计】206校园顺路代送微信小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

9、PHP 实现调整数组顺序使奇数位于偶数前面
题目: 调整数组顺序使奇数位于偶数前面 描述: 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分, 所有的偶数位于位于数组的后半部分,并保证奇数和奇数ÿ…...
iOS开发工具-网络封包分析工具Charles
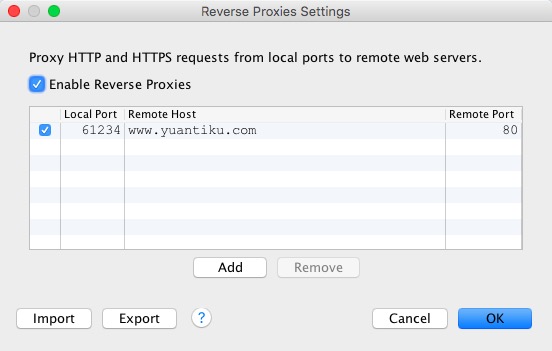
一、Charles简介 Charles 是在 Mac 下常用的网络封包截取工具,在做 移动开发时,我们为了调试与服务器端的网络通讯协议,常常需要截取网络封包来分析。 Charles 通过将自己设置成系统的网络访问代理服务器,使得所有的网络访问请求…...

7、PHP 实现矩形覆盖
题目: 矩形覆盖 描述: 我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。 请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法? <?php function rectCover($number) {$prePreNum 1;$preNum 2;$temp 0;i…...
鸿蒙开发通信与连接:【@ohos.wifiext (WLAN)】
WLAN 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 该文档中的接口只供非通用类型产品使用,如路由器等,对于常规类型产品,不应该使用这些接口。 导入模块 …...

Ps:脚本事件管理器
Ps菜单:文件/脚本/脚本事件管理器 Scripts/Script Events Manager 脚本事件管理器 Script Events Manager允许用户将特定的事件(如打开、存储或导出文件)与 JavaScript 脚本或 Photoshop 动作关联起来,以便在这些事件发生时自动触…...

redis哨兵模式下业务代码连接实现
目录 一:背景 二:实现过程 三:总结 一:背景 在哨兵模式下,真实的redis服务地址由一个固定ip转变为可以变化的ip,这样我们业务代码在连接redis的时候,就需要判断哪个主redis服务地址,哪个是从…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
