【2024最新华为OD-C/D卷试题汇总】[支持在线评测] LYA的巡演(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员
✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解
💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导
👏 感谢大家的订阅➕ 和 喜欢💗
📎在线评测链接
https://app5938.acapp.acwing.com.cn/contest/2/problem/OD1073
🌍 评测功能需要 ⇒ 订阅专栏 ⇐ 后私信联系清隆解锁~
🍓OJ题目截图
文章目录
- 📎在线评测链接
- 🍓OJ题目截图
- LYA的巡演
- 题目描述
- 输入格式
- 输出格式
- 样例输入
- 样例输出
- 样例解释
- 数据范围
- 题解
- 题解
- 参考代码
LYA的巡演
题目描述
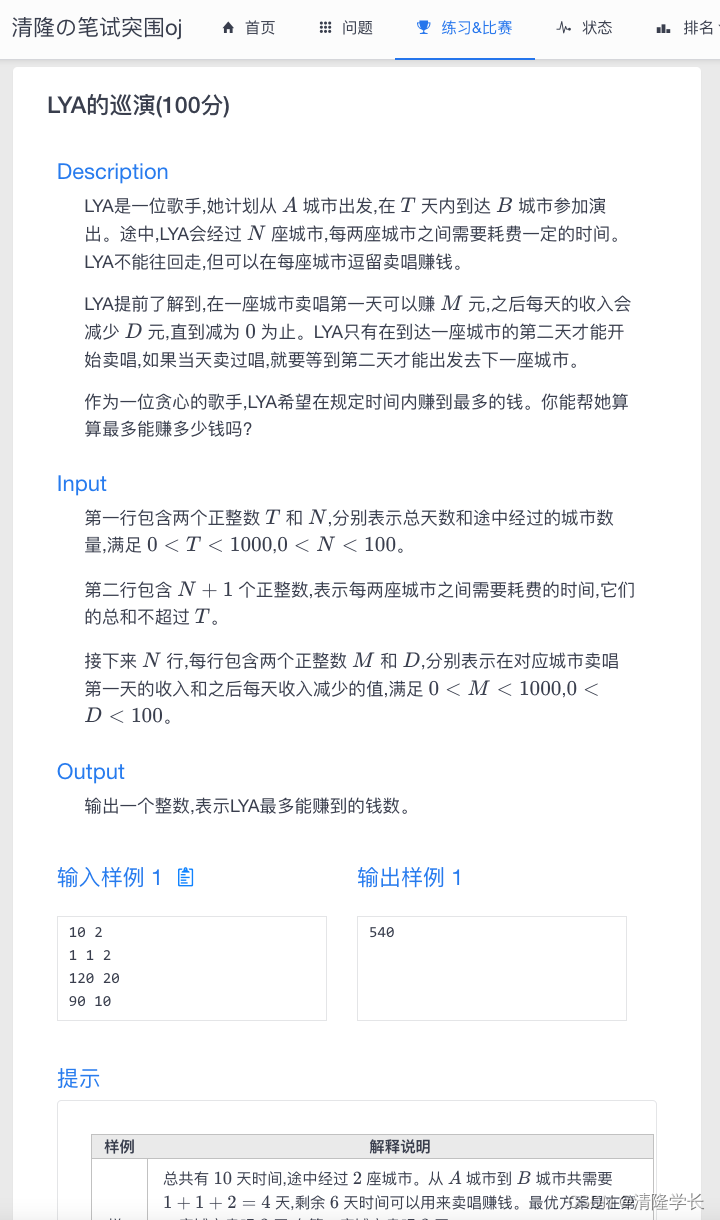
LYA是一位歌手,她计划从 A A A 城市出发,在 T T T 天内到达 B B B 城市参加演出。途中,LYA会经过 N N N 座城市,每两座城市之间需要耗费一定的时间。LYA不能往回走,但可以在每座城市逗留卖唱赚钱。
LYA提前了解到,在一座城市卖唱第一天可以赚 M M M 元,之后每天的收入会减少 D D D 元,直到减为 0 0 0 为止。LYA只有在到达一座城市的第二天才能开始卖唱,如果当天卖过唱,就要等到第二天才能出发去下一座城市。
作为一位贪心的歌手,LYA希望在规定时间内赚到最多的钱。你能帮她算算最多能赚多少钱吗?
输入格式
第一行包含两个正整数 T T T 和 N N N,分别表示总天数和途中经过的城市数量,满足 0 < T < 1000 0 < T < 1000 0<T<1000, 0 < N < 100 0 < N < 100 0<N<100。
第二行包含 N + 1 N+1 N+1 个正整数,表示每两座城市之间需要耗费的时间,它们的总和不超过 T T T。
接下来 N N N 行,每行包含两个正整数 M M M 和 D D D,分别表示在对应城市卖唱第一天的收入和之后每天收入减少的值,满足 0 < M < 1000 0 < M < 1000 0<M<1000, 0 < D < 100 0 < D < 100 0<D<100。
输出格式
输出一个整数,表示LYA最多能赚到的钱数。
样例输入
10 2
1 1 2
120 20
90 10
样例输出
540
样例解释
总共有 10 10 10 天时间,途中经过 2 2 2 座城市。从 A A A 城市到 B B B 城市共需要 1 + 1 + 2 = 4 1+1+2=4 1+1+2=4 天,剩余 6 6 6 天时间可以用来卖唱赚钱。最优方案是在第一座城市卖唱 3 3 3 天,在第二座城市卖唱 3 3 3 天。
在第一座城市可以赚 120 + 100 + 80 = 300 120+100+80=300 120+100+80=300 元,在第二座城市可以赚 90 + 80 + 70 = 240 90+80+70=240 90+80+70=240 元,总收入为 300 + 240 = 540 300+240=540 300+240=540 元。
数据范围
0 < T < 1000 0 < T < 1000 0<T<1000
0 < N < 100 0 < N < 100 0<N<100
0 < M < 1000 0 < M < 1000 0<M<1000
0 < D < 100 0 < D < 100 0<D<100
题解
抱歉,我的题解写得不够准确。根据之前给出的Python代码,这道题确实可以用贪心策略来解决。让我重新写一份题解:
题解
这道题可以使用贪心策略来解决。我们可以先计算出歌手总共有多少天可以用来卖唱赚钱,然后将每座城市每天的收入按从大到小排序,取前 k k k 大的值相加即可,其中 k k k 为可以卖唱的总天数。
具体步骤如下:
- 计算歌手总共可以卖唱的天数 k k k,即总天数 T T T 减去城市间移动需要的天数之和。
- 遍历每座城市,计算出在该城市卖唱每天的收入,直到收入减为 0 0 0,将所有的收入值加入数组 i n c o m e s incomes incomes。
- 将数组 i n c o m e s incomes incomes 按照从大到小的顺序排序。
- 取排序后的数组 i n c o m e s incomes incomes 的前 k k k 个元素求和,即为歌手能赚到的最大收入。
为什么这样做是正确的呢?因为我们要在有限的天数内尽可能多地赚钱,所以应该优先选择每天收入最高的城市去卖唱。将所有城市的每天收入排序后,前 k k k 大的收入对应的就是歌手应该选择去卖唱的日子。
这样做的时间复杂度为 O ( N × max ( M ) + k log k ) O(N \times \max(M) + k \log k) O(N×max(M)+klogk),其中 N N N 为城市数量, M M M 为某座城市第一天卖唱的收入, k k k 为可以卖唱的总天数。排序的时间复杂度为 O ( k log k ) O(k \log k) O(klogk),而遍历所有城市计算收入的时间复杂度为 O ( N × max ( M ) ) O(N \times \max(M)) O(N×max(M))。
这种贪心策略是最优的,因为它总是选择了当前收入最高的日子去卖唱,不会遗漏任何可能获得更多收入的机会。
参考代码
- Python
total_days, n = map(int, input().split())
travel_days = sum(map(int, input().split()))
sing_days = total_days - travel_daysincomes = []
for _ in range(n):first_day, dec = map(int, input().split())cur_income = first_daywhile cur_income > 0:incomes.append(cur_income)cur_income -= decincomes.sort(reverse=True)
print(sum(incomes[:sing_days]))
- Java
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int totalDays = sc.nextInt();int n = sc.nextInt();int travelDays = 0;for (int i = 0; i < n + 1; i++) {travelDays += sc.nextInt();}int singDays = totalDays - travelDays;ArrayList<Integer> incomes = new ArrayList<>();for (int i = 0; i < n; i++) {int firstDay = sc.nextInt();int dec = sc.nextInt();int curIncome = firstDay;while (curIncome > 0) {incomes.add(curIncome);curIncome -= dec;}}Collections.sort(incomes, Collections.reverseOrder());int maxIncome = 0;for (int i = 0; i < singDays; i++) {maxIncome += incomes.get(i);}System.out.println(maxIncome);}
}
- Cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int main() {int totalDays, n;cin >> totalDays >> n;int travelDays = 0;for (int i = 0; i < n + 1; i++) {int d;cin >> d;travelDays += d;}int singDays = totalDays - travelDays;vector<int> incomes;for (int i = 0; i < n; i++) {int firstDay, dec;cin >> firstDay >> dec;int curIncome = firstDay;while (curIncome > 0) {incomes.push_back(curIncome);curIncome -= dec;}}sort(incomes.begin(), incomes.end(), greater<int>());int maxIncome = 0;for (int i = 0; i < singDays; i++) {maxIncome += incomes[i];}cout << maxIncome << endl;return 0;
}
相关文章:

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] LYA的巡演(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

ChatGPT 简介
ChatGPT 是一种基于大型语言模型的对话系统,由 OpenAI 开发。它的核心是一个深度学习模型,使用了 GPT(Generative Pre-trained Transformer)架构。以下是 ChatGPT 的原理和工作机制的详细介绍: ### GPT 架构 1. **Tr…...
大数据实训室建设可行性报告
一、建设大数据实训室的背景与意义 随着信息技术的飞速发展,大数据已成为推动社会进步和经济发展的重要力量。中高职院校作为技能型人才培养的摇篮,承担着为社会输送大数据领域高素质、高技能人才的重要任务。因此,建设大数据实训室…...

学懂C#编程:让函数返回 多个返回值 的几种常用技术
1. 使用 out 或 ref 参数 out 和 ref 参数允许方法修改传入变量的值,并通过它们“返回”多个值。ref 需要变量事先初始化,而 out 不要求。 public void GetValues(out int val1, out string val2) {val1 10;val2 "Hello"; }// 使用示例 int…...

蔚来汽车AI算法工程师,如何理解注意力?
大家好啊,我是董董灿。 今天分享一个上海蔚来汽车的AI算法岗位面试经验总结帖,面试岗位为算法工程师。 这次面试提到的问题,除了与实习相关内容和反问之外,面试官总共问了8个问题,主要集中在深度学习基础概念的理解上…...
信创适配评测
概叙 信创科普参考:全面国产化之路-信创-CSDN博客 有必要再解释一下两个名词“28N”,“79号文件”,因为“28N”指定了由政府牵头从各领域开启国产化的基调,而“79号文件”则指定了国产化的截止日期2027年。 信创的本质是实现中国信…...

【Qt6.3 基础教程 04】探索Qt项目结构和配置文件
文章目录 前言Qt项目的基本结构配置文件:.pro文件基本构成示例.pro文件: qmake和构建过程步骤简述: 修改项目设置结论 前言 当你开始使用Qt进行开发时,理解项目结构和配置文件的作用是至关重要的。这篇博文将带你深入了解Qt项目的…...
SpringBoot测试实践
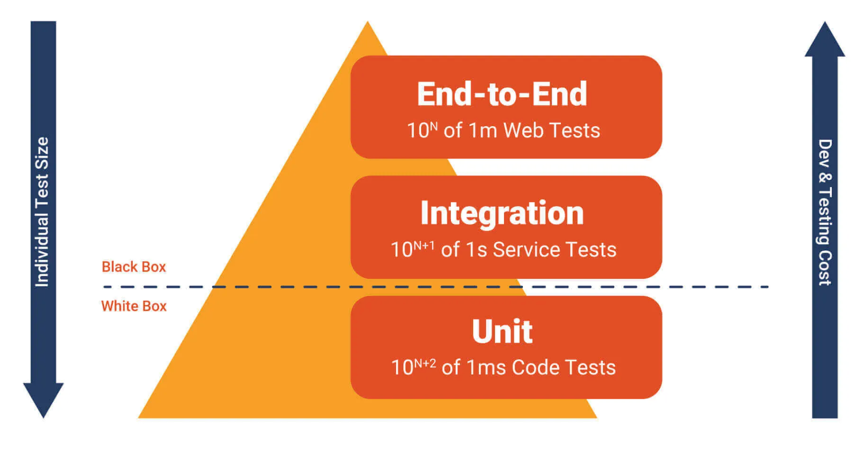
测试按照粒度可分为3层: 单元测试:单元测试(Unit Testing)又称为模块测试 ,是针对程序模块(软件设计的最小单位)来进行正确性检验的测试工作。程序单元是应用的最小可测试部件。在过程化编程中…...

Flask-OAuthlib
Flask-OAuthlib库教程 Flask-OAuthlib 是一个为 Flask 应用提供 OAuth1 和 OAuth2 支持的库。它允许开发者轻松地集成第三方 OAuth 服务,或者构建自己的 OAuth 提供者服务。 官方文档链接 Flask-OAuthlib官方文档 架构概述 Flask-OAuthlib 的主要组件包括&…...

树和森林.
目录 一、树 1.1树的存储结构 1.1.1双亲表示法 1.1.2孩子链表 1.1.3孩子兄弟表示法 1.2树与二叉树的转换 1.2.1将树转换成二叉树: 1.2.2将二叉树转换成树 二、森林 2.1森林与二叉树的转换 2.1.1将森林转换成二叉树 2.1.2二叉树转换成森林 三、树和森林的…...
ubuntu下同时安装和使用不同版本的库 librealsense
apt 安装的最新版本在/usr 源码安装的旧版本在/usr/local set(realsense2_DIR /usr/local/) find_package(realsense2 2.50.0 REQUIRED) message( "\n\n ${realsense2_INCLUDE_DIR} ${realsense2_VERSION} RealSense SDK 2.0 is FINDINGING, please install it from…...

openEuler操作系统下静默安装Oracle19c
在openEuler-23.09上安装Oracle19c,创建非容器数据库实例(含静默安装) 操作系统版本 openEuler-23.09-x86_64-dvd.iso ,安装步骤此处省略。。。 最常用且直接的方法来查看openEuler的版本号是查看/etc/os-release文件 [root@openEuler ~]$ cat /etc/os-release NAME="…...

Linux CPU常见命令行详解
在Linux系统中,命令行是管理和监控系统资源的重要工具。特别是当我们需要了解CPU的状态、性能和利用率时,一系列命令行工具就显得尤为重要。本文将详细介绍Linux中与CPU相关的常见命令行工具及其使用方法,帮助大家更好地理解和利用这些工具来…...

防止更新或保存 Laravel 模型
例如,创建模型后,我不希望任何人能够再次更新该记录。相反,它应该被全新的记录覆盖并存档。 这是一个简单的特征,您可以在模型上使用它来禁用更新: trait PreventsUpdating {public static function bootPreventsUpd…...

Cadence:Conformal系列形式验证工具
Conformal 工具最早由Verplex Systems开发。Verplex是一家专注于形式验证工具开发的公司,其核心产品是Conformal等效性检查工具。由于其技术的先进性和市场需求,Verplex的 Conformal工具迅速在半导体行业内获得了认可。 2003 年,Cadence Desi…...
一般人不要学Python?一般人怎么学Python!!
关于“建议一般人真的不要学Python”这一观点,我认为这是一个过于绝对的说法。实际上,Python作为一种流行的编程语言,具有许多优点,适合不同背景和需求的人学习。以下是一些反驳这一观点的理由: 易于学习和理解&#x…...

微服务架构中间件安装部署
微服务架构中间件安装部署 jdk安装 安装包jdk-8u144-linux-x64.tar.gz 先检查系统原版本的jdk并卸载 rpm -qa | grep java 显示信息如下: tzdata-java-2014g-1.el6.noarch java-1.6.0-openjdk-1.6.0.0-11.1.13.4.el6.x86_64 java-1.7.0-openjdk-1.7.0.65-2.5.1.2.…...

车辆数据的提取、定位和融合(其一 共十二篇)
第一篇: System Introduction 第二篇:State of the Art 第三篇:localization 第四篇:Submapping and temporal weighting 第五篇:Mapping of Point-shaped landmark data 第六篇:Clustering of landma…...

Vue3组件通信全解析:利用props、emit、provide/inject跨层级传递数据,expose与ref实现父子组件方法调用
文章目录 一、父组件数据传递N个层级的子组件vue3 provide 与 injectA组件名称 app.vueB组件名称 provideB.vueC组件名称 provideCSetup.vue 二、使用v-model指令实现父子组件的双向绑定父组件名称 app.vue子组件名称 v-modelSetup.vue 三、父组件props向子组件传值子组件 prop…...

华为---OSPF被动接口配置(四)
9.4 OSPF被动接口配置 9.4.1 原理概述 OSPF被动接口也称抑制接口,成为被动接口后,将不会接收和发送OSPF报文。如果要使OSPF路由信息不被某一网络中的路由器获得且使本地路由器不接收网络中其他路由器发布的路由更新信息,即已运行在OSPF协议…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
